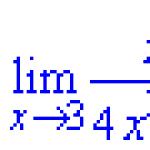Theory of limits- one of the sections of mathematical analysis that some can master, while others have difficulty calculating the limits. The question of finding limits is quite general, since there are dozens of techniques solution limits various types. The same limits can be found both using L'Hopital's rule and without it. It happens that scheduling a series of infinitesimal functions allows you to quickly obtain the desired result. There are a set of techniques and tricks that allow you to find the limit of a function of any complexity. In this article we will try to understand the main types of limits that are most often encountered in practice. We will not give the theory and definition of the limit here; there are many resources on the Internet where this is discussed. Therefore, let’s get down to practical calculations, this is where your “I don’t know! I can’t! We weren’t taught!”
Calculating limits using the substitution method
Example 1. Find the limit of a function
Lim((x^2-3*x)/(2*x+5),x=3).
Solution: Examples of this kind can be theoretically calculated using the usual substitution
The limit is 18/11.
There is nothing complicated or wise about such limits - we substituted the value, calculated it, and wrote down the limit as an answer. However, based on such limits, everyone is taught that first of all they need to substitute the value into the function. Further, the limits become more complicated, introducing the concept of infinity, uncertainty, and the like.
A limit with uncertainty like infinity divided by infinity. Uncertainty Disclosure Techniques
Example 2. Find the limit of a function
Lim((x^2+2x)/(4x^2+3x-4),x=infinity).
Solution: A limit of the form polynomial divided by a polynomial is given, and the variable tends to infinity ![]()
Simply substituting the value to which the variable should be found to find the limits will not help, we get an uncertainty of the form infinity divided by infinity.
According to the theory of limits, the algorithm for calculating the limit is to find the largest power of “x” in the numerator or denominator. Next, the numerator and denominator are simplified to it and the limit of the function is found
Since the value tends to zero when the variable approaches infinity, they are neglected, or written into the final expression in the form of zeros 
Immediately from practice, you can get two conclusions that are a hint in the calculations. If a variable tends to infinity and the degree of the numerator is greater than the degree of the denominator, then the limit is equal to infinity. Otherwise, if the polynomial in the denominator is of higher order than in the numerator, the limit is zero.
The limit can be written in formulas like this: 
If we have a function of the form an ordinary field without fractions, then its limit is equal to infinity ![]()
The next type of limits concerns the behavior of functions near zero.
Example 3. Find the limit of a function
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Solution: There is no need to remove the leading factor of the polynomial here. Exactly the opposite, you need to find the smallest power of the numerator and denominator and calculate the limit ![]()
Value x^2; x tend to zero when the variable tends to zero. Therefore, they are neglected, so we get ![]()
that the limit is 2.5.
Now you know how to find the limit of a function of the form, divide a polynomial by a polynomial if the variable tends to infinity or 0. But this is only a small and easy part of the examples. From the following material you will learn how to uncover uncertainties in the limits of a function.
Limit with uncertainty of type 0/0 and methods for its calculation
Everyone immediately remembers the rule that you cannot divide by zero. However, the theory of limits in this context implies infinitesimal functions.
Let's look at a few examples for clarity.
Example 4. Find the limit of a function
Lim((3x^2+10x+7)/(x+1), x=-1).
Solution: When we substitute the value of the variable x = -1 into the denominator, we get zero, and we get the same thing in the numerator. So we have uncertainty of the form 0/0.
Dealing with such uncertainty is simple: you need to factorize the polynomial, or rather, select the factor that turns the function into zero. 
After expansion, the limit of the function can be written as 
That's the whole method for calculating the limit of a function. We do the same if there is a limit of the form polynomial divided by a polynomial.
Example 5. Find the limit of a function
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Solution: Direct substitution shows
2*4-7*2+6=0;
3*4-2-10=0
what do we have type 0/0 uncertainty.
Let's divide the polynomials by the factor that introduces the singularity ![]()
![]()
There are teachers who teach that polynomials of 2nd order, that is, the “quadratic equations” type, should be solved through the discriminant. But real practice shows that this is longer and more confusing, so get rid of the features within the limits according to the specified algorithm. Thus, we write the function in the form of simple factors and calculate it in the limit 
As you can see, there is nothing complicated in calculating such limits. By the time you study the limits, you know how to divide polynomials, at least according to the program you should have already passed it.
Among the tasks on type 0/0 uncertainty There are some in which you need to use abbreviated multiplication formulas. But if you don’t know them, then by dividing a polynomial by a monomial you can get the desired formula.
Example 6. Find the limit of a function
Lim((x^2-9)/(x-3), x=3).
Solution: We have an uncertainty of type 0/0. In the numerator we use the abbreviated multiplication formula ![]()
and calculate the required limit ![]()
Method for revealing uncertainty by multiplying by its conjugate
The method is applied to the limits in which uncertainty is generated by irrational functions. The numerator or denominator turns to zero at the calculation point and it is not known how to find the boundary.
Example 7. Find the limit of a function
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Solution: Let's represent the variable in the limit formula
When substituting, we obtain an uncertainty of type 0/0.
According to the theory of limits, the way to bypass this feature is to multiply the irrational expression by its conjugate. To ensure that the expression does not change, the denominator must be divided by the same value 
Using the difference of squares rule, we simplify the numerator and calculate the limit of the function
We simplify the terms that create the singularity in the limit and perform the substitution
Example 8. Find the limit of a function
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Solution: Direct substitution shows that the limit has a singularity of the form 0/0. ![]()
To expand, we multiply and divide by the conjugate of the numerator 
We write down the difference of squares
We simplify the terms that introduce the singularity and find the limit of the function
![]()
Example 9. Find the limit of a function
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Solution: Substitute two into the formula ![]()
We get uncertainty 0/0.
The denominator must be multiplied by the conjugate expression, and in the numerator the quadratic equation must be solved or factored, taking into account the singularity. Since it is known that 2 is a root, we find the second root using Vieta’s theorem
Thus, we write the numerator in the form ![]()
and substitute it into the limit
By reducing the difference of squares, we get rid of the singularities in the numerator and denominator
In this way, you can get rid of singularities in many examples, and the application should be noted wherever a given difference of roots turns into zero during substitution. Other types of limits concern exponential functions, infinitesimal functions, logarithms, special limits, and other techniques. But you can read about this in the articles listed below about limits.
Elementary functions and their graphs.
The main elementary functions are: power function, exponential function, logarithmic function, trigonometric functions and inverse trigonometric functions, as well as a polynomial and a rational function, which is the ratio of two polynomials.
Elementary functions also include those functions that are obtained from elementary ones by applying the basic four arithmetic operations and forming a complex function.
Graphs of elementary functions
| Straight line- graph of a linear function y = ax + b. The function y monotonically increases for a > 0 and decreases for a< 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность) | |
 | Parabola- graph of the quadratic trinomial function y = ax 2 + bx + c. It has a vertical axis of symmetry. If a > 0, has a minimum if a< 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax 2 + bx +c =0 |
 | Hyperbola- graph of the function. When a > O it is located in the I and III quarters, when a< 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а >0) or y - - x(a< 0). |
 | Exponential function. Exhibitor(exponential function to base e) y = e x. (Another spelling y = exp(x)). Asymptote is the abscissa axis. |
 | Logarithmic function y = log a x(a > 0) |
 | y = sinx. Sine wave- periodic function with period T = 2π |
Function limit.
The function y=f(x) has a number A as a limit as x tends to a, if for any number ε › 0 there is a number δ › 0 such that | y – A | ‹ ε if |x - a| ‹ δ,
or lim y = A
Continuity of function.
The function y=f(x) is continuous at the point x = a if lim f(x) = f(a), i.e.
the limit of a function at a point x = a is equal to the value of the function at a given point.
Finding the limits of functions.
Basic theorems on the limits of functions.
1. The limit of a constant value is equal to this constant value:
2. The limit of an algebraic sum is equal to the algebraic sum of the limits of these functions:
lim (f + g - h) = lim f + lim g - lim h
3. The limit of the product of several functions is equal to the product of the limits of these functions:
lim (f * g* h) = lim f * lim g * lim h
4. The limit of the quotient of two functions is equal to the quotient of the limits of these functions if the limit of the denominator is not equal to 0:
lim------- = ----------
The first remarkable limit: lim --------- = 1
Second remarkable limit: lim (1 + 1/x) x = e (e = 2, 718281..)
Examples of finding the limits of functions.
5.1. Example:
![]()
Any limit consists of three parts:
1) The well-known limit icon.
2) Entries under the limit icon. The entry reads “X tends to one.” Most often it is x, although instead of “x” there can be any other variable. In place of one there can be absolutely any number, as well as infinity 0 or .
3) Functions under the limit sign, in this case .
The recording itself ![]() reads like this: “the limit of a function as x tends to unity.”
reads like this: “the limit of a function as x tends to unity.”
A very important question - what does the expression “x” mean? strives to one"? The expression "x" strives to one” should be understood as follows: “x” consistently takes on the values which approach unity infinitely close and practically coincide with it.
How to solve the above example? Based on the above, you just need to substitute one into the function under the limit sign:
So the first rule : When given a limit, you first simply plug the number into the function.
5.2. Example with infinity:
Let's figure out what it is? This is the case when it increases without limit.
So: if , then the function tends to minus infinity:
![]()
According to our first rule, instead of “X” we substitute in the function infinity and we get the answer.
5.3. Another example with infinity:
![]()
Again we begin to increase to infinity, and look at the behavior of the function.
Conclusion: the function increases unlimitedly![]()
5.4. A series of examples:
Try to mentally analyze the following examples yourself and solve the simplest types of limits:
, , , , ![]() , , , ,
, , , , ![]() ,
,
What do you need to remember and understand from the above?
When given any limit, first simply plug the number into the function. At the same time, you must understand and immediately solve the simplest limits, such as ![]() ,
,
etc.
,
,
etc.
6. Limits with uncertainty of type and a method for solving them.
Now we will consider the group of limits when , and the function is a fraction whose numerator and denominator contain polynomials.
6.1. Example:
Calculate limit ![]()
According to our rule, we try to substitute infinity into the function. What do we get at the top? Infinity. And what happens below? Also infinity. Thus, we have what is called species uncertainty. One might think that = 1, and the answer is ready, but in the general case this is not at all the case, and you need to apply some solution technique, which we will now consider.
How to solve limits of this type?
First we look at the numerator and find the highest power: 
The leading power in the numerator is two.
Now we look at the denominator and also find it to the highest power: 
The highest degree of the denominator is two.
Then we choose the highest power of the numerator and denominator: in this example, they are the same and equal to two.
So, the solution method is as follows: to reveal uncertainty you need to divide the numerator and denominator by in the senior degree.
![]()

Thus, the answer is not 1.
Example
Find the limit ![]()
Again in the numerator and denominator we find in the highest degree: ![]()
Maximum degree in numerator: 3
Maximum degree in denominator: 4
Choose greatest value, in this case four.
According to our algorithm, to reveal uncertainty, we divide the numerator and denominator by .

Example
Find the limit ![]()
Maximum degree of “X” in the numerator: 2
Maximum degree of “X” in the denominator: 1 (can be written as)
To reveal the uncertainty, it is necessary to divide the numerator and denominator by . The final solution might look like this:
![]()
Divide the numerator and denominator by

Solution online function limits. Find the limiting value of a function or functional sequence at a point, calculate ultimate the value of the function at infinity. determining the convergence of a number series and much more can be done thanks to our online service -. We allow you to find function limits online quickly and accurately. You yourself enter the function variable and the limit to which it tends, and our service carries out all the calculations for you, giving an accurate and simple answer. And for finding the limit online you can enter both numerical series and analytical functions containing constants in literal expression. In this case, the found limit of the function will contain these constants as constant arguments in the expression. Our service solves any complex problems of finding limits online, it is enough to indicate the function and the point at which it is necessary to calculate limit value of function. Calculating online limits, you can use various methods and rules for solving them, while checking the result obtained with solving limits online on the www.site, which will lead to the successful completion of the task - you will avoid your own mistakes and clerical errors. Or you can completely trust us and use our result in your work, without spending extra effort and time on independently calculating the limit of the function. We allow input of limit values such as infinity. It is necessary to enter a common member of a number sequence and www.site will calculate the value limit online to plus or minus infinity.
One of the basic concepts of mathematical analysis is function limit And sequence limit at a point and at infinity, it is important to be able to solve correctly limits. With our service this will not be difficult. A decision is made limits online within a few seconds, the answer is accurate and complete. The study of mathematical analysis begins with transition to the limit, limits are used in almost all areas of higher mathematics, so it is useful to have a server at hand for online limit solutions, which is the site.
We figured out the basic elementary functions.
When moving to functions of a more complex type, we will certainly encounter the appearance of expressions whose meaning is not defined. Such expressions are called uncertainties.
Let's list everything main types of uncertainties: zero divided by zero (0 by 0), infinity divided by infinity, zero multiplied by infinity, infinity minus infinity, one to the power of infinity, zero to the power of zero, infinity to the power of zero.
ALL OTHER EXPRESSIONS OF UNCERTAINTY ARE NOT AND TAKE A COMPLETELY SPECIFIC FINITE OR INFINITE VALUE.
Uncover uncertainty allows:
- simplification of the type of function (transformation of expressions using abbreviated multiplication formulas, trigonometric formulas, multiplication by conjugate expressions followed by reduction, etc.);
- use of remarkable limits;
- application of L'Hopital's rule;
- using the replacement of an infinitesimal expression with its equivalent (using a table of equivalent infinitesimals).
Let's group the uncertainties into uncertainty table. For each type of uncertainty we associate a method for its disclosure (method of finding the limit).
This table, together with the table of limits of basic elementary functions, will be your main tools in finding any limits.

Let's give a couple of examples when everything works out immediately after substituting the value and uncertainty does not arise.
Example.
Calculate limit 
Solution.
Substitute the value: 
And we immediately received an answer.
Answer:

Example.
Calculate limit ![]()
Solution.
We substitute the value x=0 into the base of our exponential power function: ![]()
That is, the limit can be rewritten as ![]()
Now let's take a look at the indicator. This is a power function. Let us turn to the table of limits for power functions with a negative exponent. From there we have ![]() And
And ![]() , therefore, we can write
, therefore, we can write ![]() .
.
Based on this, our limit will be written as: ![]()
We turn again to the table of limits, but for exponential functions with a base greater than one, from which we have:
Answer:
![]()
Let's look at examples with detailed solutions Uncovering uncertainties by transforming expressions.
Very often the expression under the limit sign needs to be slightly transformed to get rid of uncertainties.
Example.
Calculate limit
Solution.
Substitute the value: 
We have arrived at uncertainty. We look at the uncertainty table to select a solution method. Let's try to simplify the expression. 
Answer:
![]()
Example.
Calculate limit ![]()
Solution.
Substitute the value: 
We came to uncertainty (0 to 0). We look at the uncertainty table to choose a solution method and try to simplify the expression. Let's multiply both the numerator and the denominator by the expression conjugate to the denominator.
For the denominator the conjugate expression will be ![]()
We multiplied the denominator so that we could apply the abbreviated multiplication formula - difference of squares and then reduce the resulting expression. 
After a series of transformations, the uncertainty disappeared.
Answer:
![]()
COMMENT: For limits of this type, the method of multiplying by conjugate expressions is typical, so feel free to use it.
Example.
Calculate limit 
Solution.
Substitute the value: 
We have arrived at uncertainty. We look at the uncertainty table to choose a solution method and try to simplify the expression. Since both the numerator and the denominator vanish at x = 1, then if these expressions can be reduced (x-1) and the uncertainty will disappear.
Let's factorize the numerator: 
Let's factorize the denominator: 
Our limit will take the form: 
After the transformation, the uncertainty was revealed.
Answer:
![]()
Let's consider limits at infinity from power expressions. If the exponents of the power expression are positive, then the limit at infinity is infinite. Moreover, the greatest degree is of primary importance; the rest can be discarded.
Example.![]()
Example.
If the expression under the limit sign is a fraction, and both the numerator and the denominator are power expressions (m is the power of the numerator, and n is the power of the denominator), then when an uncertainty of the form infinity to infinity arises, in this case uncertainty is revealed dividing both the numerator and denominator by
Example.
Calculate limit 
The first remarkable limit is the following equality:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Since for $\alpha\to(0)$ we have $\sin\alpha\to(0)$, they say that the first remarkable limit reveals an uncertainty of the form $\frac(0)(0)$. Generally speaking, in formula (1), instead of the variable $\alpha$, any expression can be placed under the sine sign and in the denominator, as long as two conditions are met:
- The expressions under the sine sign and in the denominator simultaneously tend to zero, i.e. there is uncertainty of the form $\frac(0)(0)$.
- The expressions under the sine sign and in the denominator are the same.
Corollaries from the first remarkable limit are also often used:
\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(equation)
Eleven examples are solved on this page. Example No. 1 is devoted to the proof of formulas (2)-(4). Examples No. 2, No. 3, No. 4 and No. 5 contain solutions with detailed comments. Examples No. 6-10 contain solutions with virtually no comments, because detailed explanations were given in previous examples. The solution uses some trigonometric formulas that can be found.
Let me note that the presence of trigonometric functions coupled with the uncertainty $\frac (0) (0)$ does not necessarily mean the application of the first remarkable limit. Sometimes simple trigonometric transformations are sufficient - for example, see.
Example No. 1
Prove that $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha )(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Since $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, then:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Since $\lim_(\alpha\to(0))\cos(0)=1$ and $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , That:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
b) Let's make the change $\alpha=\sin(y)$. Since $\sin(0)=0$, then from the condition $\alpha\to(0)$ we have $y\to(0)$. In addition, there is a neighborhood of zero in which $\arcsin\alpha=\arcsin(\sin(y))=y$, so:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
The equality $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ has been proven.
c) Let's make the replacement $\alpha=\tg(y)$. Since $\tg(0)=0$, then the conditions $\alpha\to(0)$ and $y\to(0)$ are equivalent. In addition, there is a neighborhood of zero in which $\arctg\alpha=\arctg\tg(y))=y$, therefore, based on the results of point a), we will have:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
The equality $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ has been proven.
Equalities a), b), c) are often used along with the first remarkable limit.
Example No. 2
Calculate the limit $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.
Since $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ and $\lim_( x\to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. and both the numerator and denominator of the fraction simultaneously tend to zero, then here we are dealing with an uncertainty of the form $\frac(0)(0)$, i.e. done. In addition, it is clear that the expressions under the sine sign and in the denominator coincide (i.e., and is satisfied):
So, both conditions listed at the beginning of the page are met. It follows from this that the formula is applicable, i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7))=1$.
Answer: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Example No. 3
Find $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Since $\lim_(x\to(0))\sin(9x)=0$ and $\lim_(x\to(0))x=0$, then we are dealing with an uncertainty of the form $\frac(0 )(0)$, i.e. done. However, the expressions under the sine sign and in the denominator do not coincide. Here you need to adjust the expression in the denominator to the desired form. We need the expression $9x$ to be in the denominator - then it will become true. Essentially, we're missing a factor of $9$ in the denominator, which isn't that hard to enter—just multiply the expression in the denominator by $9$. Naturally, to compensate for multiplication by $9$, you will have to immediately divide by $9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Now the expressions in the denominator and under the sine sign coincide. Both conditions for the limit $\lim_(x\to(0))\frac(\sin(9x))(9x)$ are satisfied. Therefore, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. And this means that:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Answer: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Example No. 4
Find $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Since $\lim_(x\to(0))\sin(5x)=0$ and $\lim_(x\to(0))\tg(8x)=0$, here we are dealing with uncertainty of the form $\frac(0)(0)$. However, the form of the first remarkable limit is violated. A numerator containing $\sin(5x)$ requires a denominator of $5x$. In this situation, the easiest way is to divide the numerator by $5x$, and immediately multiply by $5x$. In addition, we will perform a similar operation with the denominator, multiplying and dividing $\tg(8x)$ by $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Reducing by $x$ and taking the constant $\frac(5)(8)$ outside the limit sign, we obtain:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Note that $\lim_(x\to(0))\frac(\sin(5x))(5x)$ fully satisfies the requirements for the first remarkable limit. To find $\lim_(x\to(0))\frac(\tg(8x))(8x)$ the following formula is applicable:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Answer: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Example No. 5
Find $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Since $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (remember that $\cos(0)=1$) and $\lim_(x\to(0))x^2=0$, then we are dealing with uncertainty of the form $\frac(0)(0)$. However, in order to apply the first remarkable limit, you should get rid of the cosine in the numerator, moving on to sines (in order to then apply the formula) or tangents (in order to then apply the formula). This can be done with the following transformation:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Let's go back to the limit:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
The fraction $\frac(\sin^2(5x))(x^2)$ is already close to the form required for the first remarkable limit. Let's work a little with the fraction $\frac(\sin^2(5x))(x^2)$, adjusting it to the first remarkable limit (note that the expressions in the numerator and under the sine must match):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Let's return to the limit in question:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Answer: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Example No. 6
Find the limit $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Since $\lim_(x\to(0))(1-\cos(6x))=0$ and $\lim_(x\to(0))(1-\cos(2x))=0$, then we are dealing with uncertainty $\frac(0)(0)$. Let us reveal it with the help of the first remarkable limit. To do this, let's move from cosines to sines. Since $1-\cos(2\alpha)=2\sin^2(\alpha)$, then:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Passing to sines in the given limit, we will have:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Answer: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Example No. 7
Calculate the limit $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ subject to $\alpha\neq\ beta$.
Detailed explanations were given earlier, but here we simply note that again there is uncertainty $\frac(0)(0)$. Let's move from cosines to sines using the formula
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Using this formula, we get:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\right| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Answer: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alpha^2)(2)$.
Example No. 8
Find the limit $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Since $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (remember that $\sin(0)=\tg(0)=0$) and $\lim_(x\to(0))x^3=0$, then here we are dealing with uncertainty of the form $\frac(0)(0)$. Let's break it down as follows:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Answer: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Example No. 9
Find the limit $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Since $\lim_(x\to(3))(1-\cos(x-3))=0$ and $\lim_(x\to(3))(x-3)\tg\frac(x -3)(2)=0$, then there is uncertainty of the form $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable $\alpha \to 0$). The easiest way is to introduce the variable $t=x-3$. However, for the sake of convenience of further transformations (this benefit can be seen in the course of the solution below), it is worth making the following replacement: $t=\frac(x-3)(2)$. I note that both replacements are applicable in this case, it’s just that the second replacement will allow you to work less with fractions. Since $x\to(3)$, then $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\right| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Answer: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Example No. 10
Find the limit $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2 )$.
Once again we are dealing with uncertainty $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable is $\alpha\to(0)$). The easiest way is to introduce the variable $t=\frac(\pi)(2)-x$. Since $x\to\frac(\pi)(2)$, then $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Example No. 11
Find the limits $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
In this case we don't have to use the first wonderful limit. Please note that both the first and second limits contain only trigonometric functions and numbers. Often in examples of this kind it is possible to simplify the expression located under the limit sign. Moreover, after the aforementioned simplification and reduction of some factors, the uncertainty disappears. I gave this example for only one purpose: to show that the presence of trigonometric functions under the limit sign does not necessarily mean the use of the first remarkable limit.
Since $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (remember that $\sin\frac(\pi)(2)=1$ ) and $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (let me remind you that $\cos\frac(\pi)(2)=0$), then we have dealing with uncertainty of the form $\frac(0)(0)$. However, this does not mean that we will need to use the first wonderful limit. To reveal the uncertainty, it is enough to take into account that $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
There is a similar solution in Demidovich’s solution book (No. 475). As for the second limit, as in the previous examples in this section, we have an uncertainty of the form $\frac(0)(0)$. Why does it arise? It arises because $\tg\frac(2\pi)(3)=-\sqrt(3)$ and $2\cos\frac(2\pi)(3)=-1$. We use these values to transform the expressions in the numerator and denominator. The goal of our actions is to write down the sum in the numerator and denominator as a product. By the way, often within a similar type it is convenient to change a variable, made in such a way that the new variable tends to zero (see, for example, examples No. 9 or No. 10 on this page). However, in this example there is no point in replacing, although if desired, replacing the variable $t=x-\frac(2\pi)(3)$ is not difficult to implement.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
As you can see, we didn't have to apply the first wonderful limit. Of course, you can do this if you want (see note below), but it is not necessary.
What is the solution using the first remarkable limit? show\hide
Using the first remarkable limit we get:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ right))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.