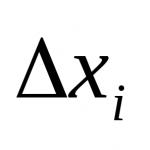What exactly is tension? It is a way of describing and measuring the strength of an electric field. Voltage itself cannot exist without an electron field around positive and negative charges. Just like a magnetic field surrounds the North and South Poles.
By modern concepts, electrons do not influence each other. An electric field is something that comes from one charge and its presence can be felt by another.
The same can be said about the concept of tension! It just helps us imagine what an electric field might look like. To be honest, it has no shape, no size, nothing like that. But the field operates with a certain force on electrons.
Forces and their action on a charged particle
A charged electron is subject to a force with some acceleration, causing it to move faster and faster. This force does work to move the electron.
Lines of force are imaginary shapes that appear around charges (determined by the electric field) and if we place any charge in that area, it will experience a force.
Properties of power lines:
- travel from north to south;
- have no mutual intersections.
Why don't the two lines of force intersect? Because this doesn't happen in real life. What is being said is a physical model and nothing more. Physicists invented it to describe the behavior and characteristics of the electric field. The model is very good at this. But remembering that this is just a model, we must know why such lines are needed.
Lines of force show:
- directions of electric fields;
- tension. The closer the lines, the greater the field strength and vice versa.
If the drawn force lines of our model intersect, the distance between them will become infinitesimal. Because of the strength of the field as a form of energy, and because of the fundamental laws of physics, this is impossible.
What is potential?
Potential is the energy that is expended to move a charged particle from the first point, which has zero potential, to the second point.
The potential difference between points A and B is the work done by forces to move a certain positive electron along an arbitrary path from A to B.

The greater the potential of the electron, the greater the flux density per unit area. This phenomenon is similar to gravity. The greater the mass, the greater the potential, the more intense and dense the gravitational field per unit area.
A small low potential charge with a reduced flux density is shown in the following figure.

And below is a charge with a high potential and flux density.

For example: during a thunderstorm, electrons are depleted at one point and collected at another, forming an electric field. When the force is sufficient to break the dielectric constant, a lightning strike (made up of electrons) is produced. When the potential difference is equalized, the electric field is destroyed.
Electrostatic field
This is a type of electric field, constant in time, formed by charges that do not move. The work of moving an electron is determined by the relations,

where r1 and r2 are the distances of the charge q to the starting and ending points of the motion trajectory. From the resulting formula it can be seen that the work done when moving a charge from point to point does not depend on the trajectory, but depends only on the beginning and end of the movement.

Every electron is subject to a force, and therefore, when an electron moves through a field, a certain amount of work is performed.
In an electrostatic field, work depends only on the final points of travel, and not on the trajectory. Therefore, when movement occurs along a closed loop, the charge returns to its original position, and the amount of work becomes equal to zero. This happens because the potential drop is zero (since the electron returns to the same point). Since the potential difference is zero, the net work will also be zero, because the falling potential is equal to the work divided by the value of the charge, expressed in coulombs.
About a uniform electric field
The electric field between two oppositely charged flat metal plates, where the lines of tension are parallel to each other, is called homogeneous.

Why is the force on the charge in such a field always the same? Thanks to symmetry. When the system is symmetric and there is only one measurement variation, all dependence disappears. There are many other fundamental reasons for the answer, but the symmetry factor is the simplest.
The work of moving a positive charge
Electric field– this is the flow of electrons from “+” to “-”, leading to high tension in the region.

Flow is the number of electric field lines passing through it. In which direction will the positive electrons move? Answer: in the direction of the electric field from positive (high potential) to negative (low potential). Therefore, a positively charged particle will move in this direction.

The field intensity at any point is defined as the force acting on a positive charge placed at that point.
The job is to transport electron particles along a conductor. According to Ohm's law, you can determine the work using different variations of formulas to carry out the calculation.
From the law of conservation of energy it follows that work is the change in energy on a separate section of the chain. Moving a positive charge against an electric field requires work to be done and results in a gain in potential energy.
Conclusion
From school curriculum We remember that an electric field is formed around charged particles. Any charge in an electric field is subject to a force, and as a result, some work is done when the charge moves. A larger charge creates a greater potential, which produces a more intense or stronger electric field. This means that there is more flow and density per unit area.
The important point is that it must be done certain force the work of moving charge from high to low potential. This reduces the charge difference between the poles. Moving electrons from current to point requires energy.
Write comments, additions to the article, maybe I missed something. Take a look, I’ll be glad if you find anything else useful on mine.
ELECTRIC CHARGE. ELEMENTARY PARTICLES.
Electric charge q - physical quantity, which determines the intensity of electromagnetic interaction.
[q] = l Cl (Coulomb).
Atoms consist of nuclei and electrons. The nucleus contains positively charged protons and uncharged neutrons. Electrons carry a negative charge. The number of electrons in an atom is equal to the number of protons in the nucleus, so overall the atom is neutral.
Charge of any body: q = ±Ne, where e = 1.6*10 -19 C is the elementary or minimum possible charge (electron charge), N- the number of excess or missing electrons. In a closed system, the algebraic sum of charges remains constant:
q 1 + q 2 + … + q n = const.
A point electric charge is a charged body whose dimensions are many times less than the distance to another electrified body interacting with it.
Coulomb's law
Two stationary point electric charges in a vacuum interact with forces directed along a straight line connecting these charges; the moduli of these forces are directly proportional to the product of the charges and inversely proportional to the square of the distance between them:
Proportionality factor
where is the electrical constant.
where 12 is the force acting from the second charge on the first, and 21 - from the first on the second.
ELECTRIC FIELD. TENSION
The fact of interaction of electric charges at a distance can be explained by the presence of an electric field around them - a material object, continuous in space and capable of acting on other charges.
The field of stationary electric charges is called electrostatic.
A characteristic of a field is its intensity.
Electric field strength at a given point is a vector whose magnitude is equal to the ratio of the force acting on a point positive charge to the magnitude of this charge, and the direction coincides with the direction of the force.
Point charge field strength Q on distance r equal to
Principle of field superposition
The field strength of a system of charges is equal to the vector sum of the field strengths of each of the charges in the system:
The dielectric constant environment is equal to the ratio of field strengths in vacuum and in matter:
It shows how many times the substance weakens the field. Coulomb's law for two point charges q And Q, located at a distance r in a medium with dielectric constant:
Field strength at a distance r from charge Q equal to
POTENTIAL ENERGY OF A CHARGED BODY IN A HOMOGENEOUS ELECTRO-STATIC FIELD
Between two large plates, charged with opposite signs and located parallel, we place a point charge q.
Since the electric field between the plates with a uniform intensity, the force acts on the charge at all points F = qE, which, when moving a charge a distance along, does work
This work does not depend on the shape of the trajectory, that is, when the charge moves q along an arbitrary line L the work will be the same.
The work of the electrostatic field to move a charge does not depend on the shape of the trajectory, but is determined exclusively by the initial and final states of the system. It, as in the case of the gravity field, is equal to the change in potential energy, taken with the opposite sign:
From a comparison with the previous formula it is clear that the potential energy of a charge in a uniform electrostatic field is equal to:
Potential energy depends on the choice of the zero level and therefore has no deep meaning in itself.
ELECTROSTATIC FIELD POTENTIAL AND VOLTAGE
Potential is a field whose operation when moving from one point of the field to another does not depend on the shape of the trajectory. The potential fields are the gravity field and the electrostatic field.
The work done by the potential field is equal to the change in the potential energy of the system, taken with the opposite sign:
Potential- the ratio of the potential energy of a charge in the field to the magnitude of this charge:
The uniform field potential is equal to
Where d- distance measured from some zero level.
Potential energy of charge interaction q with field is equal to .
Therefore, the work of the field to move a charge from a point with potential φ 1 to a point with potential φ 2 is:
The quantity is called potential difference or voltage.
The voltage or potential difference between two points is the ratio of the work done by the electric field to move charge from starting point to the final value of this charge:
[U]=1J/C=1V
FIELD STRENGTH AND POTENTIAL DIFFERENCE
When moving a charge q along the electric field line of intensity at a distance Δ d the field does work
Since by definition, we get:
Hence the electric field strength is equal to
So, the electric field strength is equal to the change in potential when moving along a field line per unit length.
If a positive charge moves in the direction of the field line, then the direction of the force coincides with the direction of movement, and the work of the field is positive:
Then, that is, the tension is directed towards decreasing potential.
Voltage is measured in volts per meter:
[E]=1 B/m
The field strength is 1 V/m if the voltage between two points of a power line located at a distance of 1 m is 1 V.
ELECTRIC CAPACITY
If we measure the charge independently Q, communicated to the body, and its potential φ, then we can find that they are directly proportional to each other:
The value C characterizes the ability of a conductor to accumulate an electric charge and is called electrical capacitance. The electrical capacity of a conductor depends on its size, shape, as well as the electrical properties of the medium.
The electrical capacity of two conductors is the ratio of the charge of one of them to the potential difference between them:
The capacity of the body is 1 F, if when a charge of 1 C is given to it, it acquires a potential of 1 V.
CAPACITORS
Capacitor- two conductors separated by a dielectric, serving to accumulate electrical charge. The charge of a capacitor is understood as the charge modulus of one of its plates or plates.
The ability of a capacitor to accumulate charge is characterized by electrical capacity, which is equal to the ratio of the capacitor charge to the voltage:
The capacitance of a capacitor is 1 F if, at a voltage of 1 V, its charge is 1 C.
The capacitance of a parallel plate capacitor is directly proportional to the area of the plates S, the dielectric constant of the medium, and is inversely proportional to the distance between the plates d:
ENERGY OF A CHARGED CAPACITOR.
Accurate experiments show that W=CU 2 /2
Because q = CU, That
Electric field energy density
Where V = Sd is the volume occupied by the field inside the capacitor. Considering that the capacitance of a parallel-plate capacitor
and the voltage on its plates U=Ed
we get:
Example. An electron, moving in an electric field from point 1 through point 2, increased its speed from 1000 to 3000 km/s. Determine the potential difference between points 1 and 2.
Metals contain conduction electrons that form electron gas and participate in thermal motion. Since conduction electrons are held inside the metal, therefore, near the surface there are forces acting on the electrons and directed into the metal. In order for an electron to leave the metal beyond its limits, a certain amount of work A must be done against these forces, which is called the work of leaving the electron from the metal. This work, naturally, is different for different metals.
The potential energy of an electron inside a metal is constant and equal to:
Wp = -eφ, where j is the electric field potential inside the metal.
21. Contact potential difference - this is the potential difference between conductors that occurs when two different conductors that have the same temperature come into contact.
When two conductors with different work functions come into contact, electric charges appear on the conductors. And a potential difference arises between their free ends. The potential difference between points located outside the conductors, near their surface, is called the contact potential difference. Since the conductors are at the same temperature, in the absence of an applied voltage the field can only exist in the boundary layers (Volta's Rule). There is an internal potential difference (when metals come into contact) and an external one (in a gap). The value of the external contact potential difference is equal to the difference in the work functions related to the electron charge. If the conductors are connected into a ring, then the EMF in the ring will be equal to 0. For different pairs of metals, the value of the contact potential difference ranges from tenths of a volt to units of volts.
The operation of a thermoelectric generator is based on the use of the thermoelectric effect, the essence of which is that when the junction (junction) of two different metals is heated, a potential difference arises between their free ends, which have a lower temperature, or the so-called thermoelectromotive force (thermo-EMF). If you close such a thermoelement (thermocouple) to an external resistance, then an electric current will flow through the circuit (Fig. 1). Thus, during thermoelectric phenomena, a direct conversion of thermal energy into electrical energy occurs.
The magnitude of the thermoelectromotive force is determined approximately by the formula E = a(T1 – T2)
22. A magnetic field - a force field acting on moving electric charges and on bodies with a magnetic moment, regardless of the state of their motion; magnetic component electro magnetic field
Moving charge q, creates a magnetic field around itself, the induction of which
where is the speed of the electron, is the distance from the electron to a given field point, μ – relative magnetic permeability of the medium, μ 0 = 4π ·10 -7 Gn/m– magnetic constant.
Magnetic induction- a vector quantity that is a force characteristic of the magnetic field (its action on charged particles) at a given point in space. Determines the force with which a magnetic field acts on a charge moving at speed.
More specifically, this is a vector such that the Lorentz force acting from the magnetic field on a charge moving with speed is equal to
23. According to the Biot-Savart-Laplace law contour element dl, through which current flows I, creates a magnetic field around itself, the induction of which at a certain point K
![]()
where is the distance from the point K to the current element dl, α – angle between the radius vector and the current element dl.
The direction of the vector can be found by Maxwell's rule(gimlet): if you screw in a gimlet with a right-hand thread in the direction of the current in the conductor element, then the direction of movement of the gimlet handle will indicate the direction of the magnetic induction vector.
Applying the Biot-Savart-Laplace law to contours various types, we get:
· in the center of a circular turn of radius R with current strength I magnetic induction
magnetic induction on the axis of circular current ![]() Where a– distance from the point at which one is searching B to the plane of the circular current,
Where a– distance from the point at which one is searching B to the plane of the circular current,
· a field created by an infinitely long conductor carrying current at a distance r from the conductor
· field created by a conductor of finite length at a distance r from the conductor (Fig. 15) ![]()
· field inside a toroid or infinitely long solenoid n– number of turns per unit length of the solenoid (toroid)
The magnetic induction vector is related to the magnetic field strength by the relation
Volumetric energy density magnetic field:
25 .On a charged particle moving in a magnetic field with induction B with speed υ , from the magnetic field there is a force called Lorentz force
and the modulus of this force is equal to ![]() .
.
The direction of the Lorentz force can be determined by left hand rule: if you place your left hand so that the component of the induction vector perpendicular to the speed enters the palm, and the four fingers are located in the direction of the speed of movement of the positive charge (or against the direction of the speed of the negative charge), then the bent thumb will indicate the direction of the Lorentz force
26 .Operating principle of cyclic charged particle accelerators.
The independence of the rotation period T of a charged particle in a magnetic field was used by the American scientist Lawrence in the idea of a cyclotron - a charged particle accelerator.
Cyclotron consists of two dees D 1 and D 2 - hollow metal half-cylinders placed in a high vacuum. An accelerating electric field is created in the gap between the dees. A charged particle entering this gap increases its speed and flies into the space of the half-cylinder (dee). The dees are placed in a constant magnetic field, and the trajectory of the particle inside the dees will be curved in a circle. When the particle enters the gap between the dees for the second time, the polarity of the electric field changes and it again becomes accelerating. An increase in speed is accompanied by an increase in the radius of the trajectory. In practice, an alternating field with a frequency ν= 1/T=(B/2π)(q/m) is applied to the dees. The speed of the particle increases each time in the interval between the dees under the influence of the electric field.
27.Ampere power is the force that acts on a conductor through which current flows I, located in a magnetic field
Δ l– length of the conductor, and direction coincides with the direction of the current in the conductor.
Ampere power module: ![]() .
.
Two parallel infinitely long straight conductors carrying currents I 1 And I 2 interact with each other with force
Where l– length of the conductor section, r– distance between conductors.
28. Interaction of parallel currents - Ampere's law
Now you can easily obtain a formula for calculating the force of interaction between two parallel currents.
So, through two long straight parallel conductors (Fig. 440), located at a distance R from each other (which is many, 15 times less than the lengths of the conductors), direct currents I 1, I 2 flow.
According to field theory, the interaction of conductors is explained as follows: an electric current in the first conductor creates a magnetic field that interacts with an electric current in the second conductor. To explain the emergence of a force acting on the first conductor, it is necessary to “switch roles” of the conductors: the second creates a field that acts on the first. Mentally rotate the right screw, rotate with your left hand (or use the cross product) and make sure that when currents flow in one direction, the conductors attract, and when currents flow in opposite directions, the conductors repel1.
Thus, the force acting on a section of length Δl of the second conductor is the Ampere force, it is equal to
![]()
where B1 is the induction of the magnetic field created by the first conductor. When writing this formula, it is taken into account that the induction vector B1 is perpendicular to the second conductor. The induction of the field created by direct current in the first conductor, at the location of the second, is equal to

From formulas (1), (2) it follows that the force acting on the selected section of the second conductor is equal to

29. A coil with current in a magnetic field.
If you place in a magnetic field not a conductor, but a coil (or coil) with current and place it vertically, then, applying the left-hand rule to the upper and lower sides of the coil, we obtain that the electromagnetic forces F acting on them will be directed in different directions. As a result of the action of these two forces, an electromagnetic torque M arises, which will cause the coil to rotate, in this case clockwise. This moment
where D is the distance between the sides of the coil.
The coil will rotate in the magnetic field until it takes a position perpendicular to the magnetic field lines (Fig. 50, b). In this position, the greatest magnetic flux will pass through the coil. Consequently, a coil or coil with current introduced into an external magnetic field always tends to take a position such that the greatest possible magnetic flux passes through the coil.
Magnetic moment, magnetic dipole moment- the main quantity characterizing the magnetic properties of a substance (the source of magnetism, according to the classical theory of electromagnetic phenomena, is electric macro- and microcurrents; a closed current is considered the elementary source of magnetism). Elementary particles have a magnetic moment, atomic nuclei, electronic shells of atoms and molecules. The magnetic moment of elementary particles (electrons, protons, neutrons and others), as shown quantum mechanics, is due to the existence of their own mechanical moment - spin.
30. Magnetic flux - a physical quantity equal to the flux density of lines of force passing through an infinitesimal area dS. Flow F in as the integral of the magnetic induction vector IN through a finite surface S Determined through an integral over the surface.
![]()
31. The work of moving a current-carrying conductor in a magnetic field
Let us consider a current-carrying circuit formed by fixed wires and a movable jumper of length l sliding along them (Fig. 2.17). This circuit is located in an external uniform magnetic field perpendicular to the plane of the circuit.

A current element I (moving wire) of length l is acted upon by an Ampere force directed to the right:
Let the conductor l move parallel to itself at a distance dx. This will do the following:
dA=Fdx=IBldx=IBdS=IdФ
The work done by a conductor on a current when moving is numerically equal to the product of the current and the magnetic flux crossed by this conductor.
The formula remains valid if a conductor of any shape moves at any angle to the lines of the magnetic induction vector.
32. Magnetization of matter . Permanent magnets can be made from only relatively few substances, but all substances placed in a magnetic field are magnetized, i.e., they themselves become sources of a magnetic field. As a result, the magnetic induction vector in the presence of matter differs from the magnetic induction vector in a vacuum.
The magnetic moment of an atom is composed of the orbital and intrinsic moments of the electrons included in its composition, as well as the magnetic moment of the nucleus (which is determined by the magnetic moments of the elementary particles included in the nucleus - protons and neutrons). The magnetic moment of the nucleus is much smaller than the moments of the electrons; therefore, when considering many issues, it can be neglected and it can be assumed that the magnetic moment of an atom is equal to the vector sum of the magnetic moments of electrons. The magnetic moment of a molecule can also be considered equal to the amount magnetic moments of the electrons included in its composition.
Thus, an atom is a complex magnetic system, and the magnetic moment of the atom as a whole is equal to the vector sum of the magnetic moments of all electrons

Magnetics and are called substances that can be magnetized in an external magnetic field, i.e. capable of creating their own magnetic field. The intrinsic field of substances depends on the magnetic properties of their atoms. In this sense, magnets are magnetic analogues of dielectrics.
According to classical concepts, an atom consists of electrons moving in orbits around a positively charged nucleus, which in turn consists of protons and neutrons.
All substances are magnetic, i.e. all substances are magnetized in an external magnetic field, but the nature and degree of magnetization are different. Depending on this, all magnets are divided into three types: 1) diamagnetic; 2) paramagnetic materials; 3) ferromagnets.
Diamagnets. - these include many metals (for example, copper, zinc, silver, mercury, bismuth), most gases, phosphorus, sulfur, quartz, water, the vast majority organic compounds etc.
Diamagnets are characterized by the following properties:
2) its own magnetic field is directed against the external one and slightly weakens it (m<1);
3) there is no residual magnetism (the diamagnetic’s own magnetic field disappears after the external field is removed).
The first two properties indicate that the relative magnetic permeability m of diamagnetic materials is only slightly less than 1. For example, the strongest of diamagnetic materials, bismuth, has m = 0.999824.
Paramagnets- These include alkali and alkaline earth metals, aluminum, tungsten, platinum, oxygen, etc.
Paramagnetic materials are characterized by the following properties:
1) very weak magnetization in an external magnetic field;
2) the own magnetic field is directed along the external one and slightly enhances it (m>1);
3) there is no residual magnetism.
From the first two properties it follows that the value of m is only slightly greater than 1. For example, for one of the strongest paramagnets - platinum - the relative magnetic permeability m = 1.00036.
33.Ferromagnets - These include iron, nickel, cobalt, gadolinium, their alloys and compounds, as well as some alloys and compounds of manganese and chromium with non-ferromagnetic elements. All these substances have ferromagnetic properties only in the crystalline state.
Ferromagnets are characterized by the following properties:
1) very strong magnetization;
2) the own magnetic field is directed along the external one and significantly enhances it (the values of m range from several hundred to several hundred thousand);
3) relative magnetic permeability m depends on the magnitude of the magnetizing field;
4) there is residual magnetism.
Domain- a macroscopic region in a magnetic crystal in which the orientation of the spontaneous homogeneous magnetization vector or the antiferromagnetism vector (at a temperature below the Curie or Néel point, respectively) in a certain - strictly ordered - manner is rotated or shifted, that is, polarized, relative to the directions of the corresponding vector in neighboring domains.
Domains are formations consisting of a huge number of [ordered] atoms and are sometimes visible to the naked eye (sizes on the order of 10−2 cm3).
Domains exist in ferro- and antiferromagnetic, ferroelectric crystals and other substances with spontaneous long-range order.
Curie point, or Curie temperature,- the temperature of a second-order phase transition associated with an abrupt change in the symmetry properties of a substance (for example, magnetic - in ferromagnets, electric - in ferroelectrics, crystal chemical - in ordered alloys). Named after P. Curie. At a temperature T below the Curie point Q, ferromagnets have spontaneous magnetization and a certain magnetic-crystalline symmetry. At the Curie point (T=Q), the intensity of the thermal motion of the atoms of a ferromagnet is sufficient to destroy its spontaneous magnetization (“magnetic order”) and change its symmetry, as a result the ferromagnet becomes paramagnetic. Similarly, for antiferromagnets at T=Q (at the so-called antiferromagnetic Curie point or Néel point), their characteristic magnetic structure (magnetic sublattices) is destroyed, and antiferromagnets become paramagnetic. In ferroelectrics and antiferroelectrics at T=Q, the thermal motion of atoms reduces to zero the spontaneous ordered orientation of the electric dipoles of elementary cells crystal lattice. In ordered alloys, at the Curie point (in the case of alloys, it is also called the point.
Magnetic hysteresis observed in magnetically ordered substances (in a certain temperature range), for example, in ferromagnets, usually divided into domains of a region of spontaneous (spontaneous) magnetization, in which the magnitude of magnetization (magnetic moment per unit volume) is the same, but the directions are different.
Under the influence of an external magnetic field, the number and size of domains magnetized by the field increase at the expense of other domains. The magnetization vectors of individual domains can rotate along the field. In a sufficiently strong magnetic field, the ferromagnet is magnetized to saturation, and it consists of one domain with saturation magnetization JS directed along the external field H.
Typical dependence of magnetization on magnetic field in the case of hysteresis

34. Earth's magnetic field
As you know, a magnetic field is a special type of force field that affects bodies with magnetic properties, as well as moving electric charges. To a certain extent, a magnetic field can be considered a special type of matter that transmits information between electric charges and bodies with a magnetic moment. Accordingly, the Earth's magnetic field is a magnetic field that is created due to factors related to the functional characteristics of our planet. That is, the geomagnetic field is created by the Earth itself, and not by external sources, although the latter have a certain effect on the planet’s magnetic field.
Thus, the properties of the Earth's magnetic field inevitably depend on the characteristics of its origin. The main theory explaining the emergence of this force field is associated with the flow of currents in the liquid metal core of the planet (the temperature at the core is so high that the metals are in a liquid state). The energy of the Earth's magnetic field is generated by the so-called hydromagnetic dynamo mechanism, which is caused by the multidirectionality and asymmetry of electric currents. They generate increased electrical discharges, which leads to the release of thermal energy and the emergence of new magnetic fields. Interestingly, the hydromagnetic dynamo mechanism has the ability to “self-excite,” that is, active electrical activity within the earth’s core constantly generates a geomagnetic field without external influence.
35.Magnetization - vector physical quantity characterizing the magnetic state of a macroscopic physical body. It is usually designated M. It is defined as the magnetic moment of a unit volume of a substance:
Here, M is the magnetization vector; - vector of the magnetic moment; V - volume.
In the general case (the case of a non-uniform, for one reason or another, medium) magnetization is expressed as
and is a function of coordinates. Where is the total magnetic moment of molecules in the volume dV The relationship between M and the magnetic field strength H in diamagnetic and paramagnetic materials is usually linear (at least when the magnetizing field is not too large):
where χm is called magnetic susceptibility. In ferromagnetic materials there is no unambiguous relationship between M and H due to magnetic hysteresis, and the magnetic susceptibility tensor is used to describe the dependence.
Magnetic field strength(standard designation H) is a vector physical quantity equal to the difference between the magnetic induction vector B and the magnetization vector M.
In the International System of Units (SI): H = (1/µ 0)B - M where µ 0 is the magnetic constant.
Magnetic permeability- physical quantity, coefficient (depending on the properties of the medium) characterizing the relationship between magnetic induction B and magnetic field strength H in the substance. This coefficient is different for different media, so they talk about the magnetic permeability of a particular medium (meaning its composition, state, temperature, etc.).
Usually denoted by the Greek letter µ. It can be either a scalar (for isotropic substances) or a tensor (for anisotropic substances).
In general, the relationship between magnetic induction and magnetic field strength through magnetic permeability is introduced as
and in the general case here it should be understood as a tensor, which in component notation corresponds to
§ 104. Work function of electrons leaving a metal
Experience shows that free electrons practically do not leave the metal at ordinary temperatures. Consequently, there must be a retarding electric field in the surface layer of the metal, preventing electrons from escaping from the metal into the surrounding vacuum. The work required to remove an electron from a metal into a vacuum is called work function. Let us indicate two probable reasons for the appearance of the work function:
1. If an electron is removed from a metal for some reason, then an excess positive charge arises in the place where the electron left and the electron is attracted to the positive charge induced by itself.
2. Individual electrons, leaving the metal, move away from it at distances on the order of atomic and thereby create an “electron cloud” above the surface of the metal, the density of which quickly decreases with distance. This cloud, together with the outer layer of positive ions of the lattice, forms electrical double layer, the field of which is similar to the field of a parallel-plate capacitor. The thickness of this layer is equal to several interatomic distances (10–10–10–9 m). It does not create an electric field in external space, but prevents free electrons from escaping from the metal.
Thus, when an electron leaves the metal, it must overcome the electric field of the double layer that retards it. Potential difference in this layer, called surface potential jump, is determined by the work function ( A) electron from metal:
Where e - electron charge. Since there is no electric field outside the double layer, the potential of the medium is zero, and inside the metal the potential is positive and equal to . The potential energy of a free electron inside a metal is - e and is negative relative to vacuum. Based on this, we can assume that the entire volume of the metal for conduction electrons represents a potential well with a flat bottom, the depth of which is equal to the work function A.
The work function is expressed in electron volts(eV): 1 eV is equal to the work done by field forces when moving an elementary electric charge (a charge equal to the charge of an electron) when it passes through a potential difference of 1 V. Since the charge of an electron is 1.610 –19 C, then 1 eV = 1.610 –19 J.
The work function depends on chemical nature metals and the purity of their surface and fluctuates within a few electron volts (for example, potassium A= 2.2 eV, for platinum A=6.3 eV). By choosing a surface coating in a certain way, you can significantly reduce the work function. For example, if you apply tungsten to the surface (A= 4,5eV) layer of alkaline earth metal oxide (Ca, Sr, Ba), then the work function is reduced to 2 eV.
§ 105. Emission phenomena and their application
If we provide the electrons in metals with the energy necessary to overcome the work function, then some of the electrons can leave the metal, resulting in the phenomenon of electron emission, or electronic emissions. Depending on the method of imparting energy to electrons, thermionic, photoelectronic, secondary electron and field emission are distinguished.
1. Thermionic emission is the emission of electrons by heated metals. The concentration of free electrons in metals is quite high, therefore, even at average temperatures, due to the distribution of electron velocities (energies), some electrons have sufficient energy to overcome the potential barrier at the metal boundary. With increasing temperature, the number of electrons, the kinetic energy of thermal motion of which is greater than the work function, increases and the phenomenon of thermionic emission becomes noticeable.
The study of the laws of thermionic emission can be carried out using the simplest two-electrode lamp - vacuum diode, which is an evacuated cylinder containing two electrodes: a cathode K and anode A. In the simplest case, the cathode is a filament made of a refractory metal (for example, tungsten), heated by an electric current. The anode most often takes the form of a metal cylinder surrounding the cathode. If the diode is connected to the circuit, as shown in Fig. 152, then when the cathode is heated and a positive voltage is applied to the anode (relative to the cathode), a current arises in the anode circuit of the diode. If you change the polarity of the battery B and then the current stops, no matter how hot the cathode is heated. Consequently, the cathode emits negative particles - electrons.
If we maintain the temperature of the heated cathode constant and remove the dependence of the anode current I and from the anode voltage U A, - current-voltage characteristic(Fig. 153), it turns out that it is not linear, that is, for a vacuum diode Ohm’s law is not satisfied. Dependence of thermionic current I from the anode voltage in the region of small positive values U described law of three second(established by Russian physicist S. A. Boguslavsky (1883-1923) and American physicist I. Langmuir (1881-1957)):

Where IN- coefficient depending on the shape and size of the electrodes, as well as their relative position.

As the anode voltage increases, the current increases to a certain maximum value I us, called saturation current. This means that almost all the electrons leaving the cathode reach the anode, so a further increase in field strength cannot lead to an increase in thermionic current. Consequently, the saturation current density characterizes the emissivity of the cathode material.
The saturation current density is determined Richardson - Deshman formula, derived theoretically on the basis of quantum statistics:

Where A - work function of electrons leaving the cathode, T - thermodynamic temperature, WITH- constant, theoretically equal milking of all metals (this is not confirmed by experiment, which is apparently explained by surface effects). A decrease in the work function leads to a sharp increase in the saturation current density. Therefore, oxide cathodes are used (for example, nickel coated with an alkaline earth metal oxide), the work function of which is 1-1.5 eV.
In Fig. 153 shows the current-voltage characteristics for two cathode temperatures: T 1 and T 2, and T 2 >T 1 . WITH As the temperature of the cathode increases, the emission of electrons from the cathode becomes more intense, and the saturation current also increases. At U a =0, an anode current is observed, i.e., some electrons emitted by the cathode have sufficient energy to overcome the work function and reach the anode without applying an electric field.
The phenomenon of thermionic emission is used in devices in which it is necessary to obtain a flow of electrons in a vacuum, for example in vacuum tubes, X-ray tubes, electron microscopes, etc. Electron tubes are widely used in electrical and radio engineering, automation and telemechanics for rectifying alternating currents, amplification electrical signals and alternating currents, generating electromagnetic oscillations, etc. Depending on the purpose, additional control electrodes are used in the lamps.
2. Photoelectron emission is the emission of electrons from a metal under the influence of light, as well as short-wave electromagnetic radiation (for example, X-rays). The main principles of this phenomenon will be discussed when considering the photoelectric effect.
3. Secondary electron emission- is the emission of electrons from the surface of metals, semiconductors or dielectrics when bombarded with a beam of electrons. The secondary electron flow consists of electrons reflected by the surface (elastically and inelastically reflected electrons), and “true” secondary electrons - electrons knocked out of the metal, semiconductor or dielectric by primary electrons.
Secondary electron number ratio n 2 to the number of primary n 1 , causing the emission is called secondary electron emission factor:

Coefficient depends on the nature of the surface material, the energy of the bombarding particles and their angle of incidence on the surface. In semiconductors and dielectrics more than metals. This is explained by the fact that in metals where the concentration of conduction electrons is high, secondary electrons, often colliding with them, lose their energy and cannot leave the metal. In semiconductors and dielectrics, due to the low concentration of conduction electrons, collisions of secondary electrons with them occur much less frequently and the probability of secondary electrons leaving the emitter increases several times.
For example in Fig. 154 shows the qualitative dependence of the secondary electron emission coefficient from energy E incident electrons for KCl. With increasing electron energy increases as primary electrons penetrate deeper into the crystal lattice and, therefore, knock out more secondary electrons. However, at some energy of the primary electrons begins to decrease. This is due to the fact that as the depth of penetration of primary electrons increases, it becomes increasingly difficult for secondary electrons to escape to the surface. Meaning max for KCl reaches12 (for pure metals it does not exceed 2).
The phenomenon of secondary electron emission is used in photomultiplier tubes(PMT), applicable to amplify weak electrical currents. The photomultiplier is a vacuum tube with a photocathode K and anode A, between which there are several electrodes - emitters(Fig. 155). Electrons, torn from the photocathode under the influence of light, enter the emitter E 1, passing through the accelerating potential difference between K and E 1. E 1 is knocked out of the emitter electrons. The electron flow thus amplified is directed to the emitter E 2, and the multiplication process is repeated on all subsequent emitters. If the PMT contains n emitters, then at anode A, called collector, turns out to be reinforced in n times the photoelectron current.
4. Autoelectronic emissions is the emission of electrons from the surface of metals under the influence of a strong external electric field. These phenomena can be observed in an evacuated tube, the configuration of the electrodes of which (cathode - tip, anode - inner surface of the tube) allows, at voltages of approximately 10 3 V, to obtain electric fields with a strength of approximately 10 7 V / m. With a gradual increase in voltage, already at a field strength at the cathode surface of approximately 10 5 -10 6 V/m, a weak current arises due to the electrons emitted by the cathode. The strength of this current increases with increasing voltage across the tube. Currents arise when the cathode is cold, so the described phenomenon is also called cold emission. An explanation of the mechanism of this phenomenon is possible only on the basis of quantum theory.

For every charge in an electric field there is a force that can move this charge. Determine the work A of moving a point positive charge q from point O to point n, performed by the forces of the electric field of a negative charge Q. According to Coulomb’s law, the force moving the charge is variable and equal to
Where r is the variable distance between charges.

![]() . This expression can be obtained like this:
. This expression can be obtained like this:
![]()
The quantity represents the potential energy W p of the charge at a given point in the electric field:
The sign (-) shows that when a charge is moved by a field, its potential energy decreases, turning into the work of movement.
A value equal to the potential energy of a unit positive charge (q = +1) is called the electric field potential.
Then ![]() . For q = +1.
. For q = +1.
Thus, the potential difference between two points of the field is equal to the work of the field forces to move a unit positive charge from one point to another.
The potential of an electric field point is equal to the work done to move a unit positive charge from a given point to infinity: . Unit of measurement - Volt = J/C.
The work of moving a charge in an electric field does not depend on the shape of the path, but depends only on the potential difference between the starting and ending points of the path.
A surface at all points of which the potential is the same is called equipotential.
The field strength is its power characteristic, and the potential is its energy characteristic.
The relationship between field strength and its potential is expressed by the formula
![]() ,
,
the sign (-) is due to the fact that the field strength is directed in the direction of decreasing potential, and in the direction of increasing potential.
5. Use of electric fields in medicine.
Franklinization, or “electrostatic shower”, is a therapeutic method in which the patient’s body or certain parts of it are exposed to a constant high-voltage electric field.
The constant electric field during the general exposure procedure can reach 50 kV, with local exposure 15 - 20 kV.
Mechanism of therapeutic action. The franklinization procedure is carried out in such a way that the patient’s head or another part of the body becomes like one of the capacitor plates, while the second is an electrode suspended above the head or installed above the site of exposure at a distance of 6 - 10 cm. Under the influence of high voltage under the tips of the needles attached to the electrode, air ionization occurs with the formation of air ions, ozone and nitrogen oxides.
Inhalation of ozone and air ions causes a reaction in the vascular network. After a short-term spasm of blood vessels, capillaries expand not only in superficial tissues, but also in deep ones. As a result, metabolic and trophic processes are improved, and in the presence of tissue damage, the processes of regeneration and restoration of functions are stimulated.
As a result of improved blood circulation, normalization of metabolic processes and nerve function, there is a decrease in headaches, high blood pressure, increased vascular tone, and a decrease in pulse.
The use of franklinization is indicated for functional disorders nervous system
Examples of problem solving
1. When the franklinization apparatus operates, 500,000 light air ions are formed every second in 1 cm 3 of air. Determine the work of ionization required to create the same amount of air ions in 225 cm 3 of air during a treatment session (15 min). The ionization potential of air molecules is assumed to be 13.54 V, and air is conventionally considered to be a homogeneous gas.
![]() - ionization potential, A - ionization work, N - number of electrons.
- ionization potential, A - ionization work, N - number of electrons.
2. When treating with an electrostatic shower, a potential difference of 100 kV is applied to the electrodes of the electric machine. Determine how much charge passes between the electrodes during one treatment procedure, if it is known that the electric field forces do 1800 J of work.
From here ![]()
Electric dipole in medicine
According to Einthoven's theory, which underlies electrocardiography, the heart is electric dipole, located in the center of an equilateral triangle (Einthoven triangle), the vertices of which can conventionally be considered 
located in the right hand, left hand and left leg.
During the cardiac cycle, both the position of the dipole in space and the dipole moment change. Measuring the potential difference between the vertices of the Einthoven triangle allows us to determine the relationship between the projections of the dipole moment of the heart onto the sides of the triangle as follows:
Knowing the voltages U AB, U BC, U AC, you can determine how the dipole is oriented relative to the sides of the triangle.
In electrocardiography, the potential difference between two points on the body (in this case, between the vertices of Einthoven's triangle) is called a lead.
Registration of the potential difference in leads depending on time is called electrocardiogram.
The geometric location of the end points of the dipole moment vector during the cardiac cycle is called vector cardiogram.
Lecture No. 4
Contact phenomena
1. Contact potential difference. Volta's laws.
2. Thermoelectricity.
3. Thermocouple, its use in medicine.
4. Resting potential. Action potential and its distribution.
- Contact potential difference. Volta's laws.
When dissimilar metals come into close contact, a potential difference arises between them, depending only on their chemical composition and temperature (Volta's first law). This potential difference is called contact.
In order to leave the metal and go into the environment, the electron must do work against the forces of attraction towards the metal. This work is called the work function of an electron leaving the metal.

Let us bring into contact two different metals 1 and 2, having work function A 1 and A 2, respectively, and A 1< A 2 . Очевидно, что свободный электрон, попавший в процессе теплового движения на поверхность раздела металлов, будет втянут во второй металл, так как со стороны этого металла на электрон действует большая сила притяжения (A 2 >A 1). Consequently, through the contact of metals, free electrons are “pumped” from the first metal to the second, as a result of which the first metal is charged positively, the second - negatively. The potential difference that arises in this case creates an electric field of intensity E, which makes it difficult for further “pumping” of electrons and will completely stop when the work of moving an electron due to the contact potential difference becomes equal to the difference in the work functions:
![]() (1)
(1)
Let us now bring into contact two metals with A 1 = A 2, having different concentrations of free electrons n 01 > n 02. Then the preferential transfer of free electrons from the first metal to the second will begin. As a result, the first metal will be charged positively, the second - negatively. A potential difference will arise between the metals, which will stop further electron transfer. The resulting potential difference is determined by the expression:
![]() , (2)
, (2)
where k is Boltzmann's constant.
In the general case of contact between metals that differ in both the work function and the concentration of free electrons, the cr.r.p. from (1) and (2) will be equal to:
![]() (3)
(3)
It is easy to show that the sum of the contact potential differences of series-connected conductors is equal to the contact potential difference created by the end conductors and does not depend on the intermediate conductors:
This position is called Volta's second law.

If we now directly connect the end conductors, then the potential difference existing between them is compensated by an equal potential difference that arises in contact 1 and 4. Therefore, the c.r.p. does not create current in a closed circuit of metal conductors having the same temperature.

2. Thermoelectricity is the dependence of the contact potential difference on temperature.
Let's make a closed circuit of two dissimilar metal conductors 1 and 2.

The temperatures of contacts a and b will be maintained at different temperatures T a > T b . Then, according to formula (3), c.r.p. in the hot junction more than in the cold junction: . As a result, a potential difference arises between junctions a and b, called thermoelectromotive force, and current I will flow in the closed circuit. Using formula (3), we obtain
Where ![]() for each pair of metals.
for each pair of metals.
- Thermocouple, its use in medicine.
A closed circuit of conductors that creates current due to differences in contact temperatures between the conductors is called thermocouple.

From formula (4) it follows that the thermoelectromotive force of a thermocouple is proportional to the temperature difference of the junctions (contacts).
Formula (4) is also valid for temperatures on the Celsius scale:
A thermocouple can only measure temperature differences. Typically one junction is maintained at 0ºC. It's called the cold junction. The other junction is called the hot or measuring junction.
The thermocouple has significant advantages over mercury thermometers: it is sensitive, inertia-free, allows you to measure the temperature of small objects, and allows remote measurements.
Measuring the temperature field profile of the human body.
It is believed that the human body temperature is constant, but this constancy is relative, since in different parts of the body the temperature is not the same and varies depending on the functional state of the body.
Skin temperature has its own well-defined topography. The lowest temperature (23-30º) is found in the distal limbs, tip of the nose, and ears. The highest temperature is in the armpits, perineum, neck, lips, cheeks. The remaining areas have a temperature of 31 - 33.5 ºС.
In a healthy person, the temperature distribution is symmetrical relative to the midline of the body. Violation of this symmetry serves as the main criterion for diagnosing diseases by constructing a temperature field profile using contact devices: a thermocouple and a resistance thermometer.
4. Resting potential. Action potential and its distribution.
The surface membrane of a cell is not equally permeable to different ions. In addition, the concentration of any specific ions is different on different sides of the membrane; the most favorable composition of ions is maintained inside the cell. These factors lead to the appearance in a normally functioning cell of a potential difference between the cytoplasm and environment(resting potential)
When excited, the potential difference between the cell and the environment changes, an action potential arises, which propagates in the nerve fibers.
The mechanism of action potential propagation along a nerve fiber is considered by analogy with the propagation of an electromagnetic wave along a two-wire line. However, along with this analogy, there are also fundamental differences.
An electromagnetic wave, propagating in a medium, weakens as its energy dissipates, turning into the energy of molecular-thermal motion. The source of energy of an electromagnetic wave is its source: generator, spark, etc.
The excitation wave does not decay, since it receives energy from the very medium in which it propagates (the energy of the charged membrane).
Thus, the propagation of an action potential along a nerve fiber occurs in the form of an autowave. The active environment is excitable cells.
Examples of problem solving
1. When constructing a profile of the temperature field of the surface of the human body, a thermocouple with a resistance of r 1 = 4 Ohms and a galvanometer with a resistance of r 2 = 80 Ohms are used; I=26 µA at a junction temperature difference of ºС. What is the thermocouple constant?
The thermopower arising in a thermocouple is equal to , where thermocouples is the temperature difference between the junctions.
According to Ohm's law, for a section of the circuit where U is taken as . Then
Lecture No. 5
Electromagnetism
1. The nature of magnetism.
2. Magnetic interaction of currents in a vacuum. Ampere's law.
4. Dia-, para- and ferromagnetic substances. Magnetic permeability and magnetic induction.
5. Magnetic properties of body tissues.
1. The nature of magnetism.
A magnetic field arises around moving electric charges (currents), through which these charges interact with magnetic or other moving electric charges.
A magnetic field is a force field and is represented by magnetic lines of force. Unlike electric field lines, magnetic field lines are always closed.
The magnetic properties of a substance are caused by elementary circular currents in the atoms and molecules of this substance.
2 . Magnetic interaction of currents in a vacuum. Ampere's law.
The magnetic interaction of currents was studied using moving wire circuits. Ampere established that the magnitude of the force of interaction between two small sections of conductors 1 and 2 with currents is proportional to the lengths of these sections, the current strengths I 1 and I 2 in them and is inversely proportional to the square of the distance r between the sections:

It turned out that the force of influence of the first section on the second depends on their relative position and is proportional to the sines of the angles and .
where is the angle between and the radius vector r 12 connecting with, and is the angle between and the normal n to the plane Q containing the section and the radius vector r 12.
Combining (1) and (2) and introducing the proportionality coefficient k, we obtain the mathematical expression of Ampere’s law:
![]() (3)
(3)

The direction of the force is also determined by the gimlet rule: it coincides with the direction forward motion a gimlet whose handle rotates from normal n 1.
A current element is a vector equal in magnitude to the product Idl of an infinitely small section of length dl of a conductor and the current strength I in it and directed along this current. Then, passing in (3) from small to infinitesimal dl, we can write Ampere’s law in differential form:
![]() . (4)
. (4)

The coefficient k can be represented as
where is the magnetic constant (or magnetic permeability of vacuum).
The value for rationalization taking into account (5) and (4) will be written in the form
![]() . (6)
. (6)
3 . Magnetic field strength. Ampere's formula. Biot-Savart-Laplace Law.
Since electric currents interact with each other through their magnetic fields, a quantitative characteristic of the magnetic field can be established on the basis of this interaction - Ampere's law. To do this, we divide the conductor l with current I into many elementary sections dl. It creates a field in space.
At point O of this field, located at a distance r from dl, we place I 0 dl 0. Then, according to Ampere’s law (6), a force will act on this element
![]() (7)
(7)
where is the angle between the direction of current I in the section dl (creating the field) and the direction of the radius vector r, and is the angle between the direction of current I 0 dl 0 and the normal n to the plane Q containing dl and r.

In formula (7) we select the part that does not depend on the current element I 0 dl 0, denoting it by dH:
Biot-Savart-Laplace law (8)
The value of dH depends only on the current element Idl, which creates a magnetic field, and on the position of point O.
The value dH is quantitative characteristics magnetic field and is called magnetic field strength. Substituting (8) into (7), we get
where is the angle between the direction of the current I 0 and the magnetic field dH. Formula (9) is called the Ampere formula and expresses the dependence of the force with which the magnetic field acts on the current element I 0 dl 0 located in it on the strength of this field. This force is located in the Q plane perpendicular to dl 0. Its direction is determined by the “left hand rule”.
Assuming =90º in (9), we get:
Those. The magnetic field strength is directed tangentially to the field line and is equal in magnitude to the ratio of the force with which the field acts on a unit current element to the magnetic constant.
4 . Diamagnetic, paramagnetic and ferromagnetic substances. Magnetic permeability and magnetic induction.
All substances placed in a magnetic field acquire magnetic properties, i.e. are magnetized and therefore change the external field. In this case, some substances weaken the external field, while others strengthen it. The first ones are called diamagnetic, second – paramagnetic substances. Among paramagnetic substances, a group of substances stands out sharply, causing a very large increase in the external field. This ferromagnets.
Diamagnets- phosphorus, sulfur, gold, silver, copper, water, organic compounds.
Paramagnets- oxygen, nitrogen, aluminum, tungsten, platinum, alkali and alkaline earth metals.
Ferromagnets– iron, nickel, cobalt, their alloys.
The geometric sum of the orbital and spin magnetic moments of electrons and the intrinsic magnetic moment of the nucleus forms the magnetic moment of an atom (molecule) of a substance.
In diamagnetic materials, the total magnetic moment of an atom (molecule) is zero, because magnetic moments cancel each other out. However, under the influence of an external magnetic field, a magnetic moment is induced in these atoms, directed opposite to the external field. As a result, the diamagnetic medium becomes magnetized and creates its own magnetic field, directed opposite to the external one and weakening it.

The induced magnetic moments of diamagnetic atoms are preserved as long as an external magnetic field exists. When the external field is eliminated, the induced magnetic moments of the atoms disappear and the diamagnetic material is demagnetized.
In paramagnetic atoms, the orbital, spin, and nuclear moments do not compensate each other. However, atomic magnetic moments are arranged randomly, so the paramagnetic medium does not exhibit magnetic properties. An external field rotates the paramagnetic atoms so that their magnetic moments are established predominantly in the direction of the field. As a result, the paramagnetic material becomes magnetized and creates its own magnetic field, coinciding with the external one and enhancing it.
(4), where is the absolute magnetic permeability of the medium. In vacuum =1, , and
In ferromagnets there are regions (~10 -2 cm) with identically oriented magnetic moments of their atoms. However, the orientation of the domains themselves is varied. Therefore, in the absence of an external magnetic field, the ferromagnet is not magnetized.
With the appearance of an external field, domains oriented in the direction of this field begin to increase in volume due to neighboring domains having different orientations of the magnetic moment; the ferromagnet becomes magnetized. With a sufficiently strong field, all domains are reoriented along the field, and the ferromagnet is quickly magnetized to saturation.

When the external field is eliminated, the ferromagnet is not completely demagnetized, but retains residual magnetic induction, since thermal motion cannot disorient the domains. Demagnetization can be achieved by heating, shaking or applying a reverse field.
At a temperature equal to the Curie point, thermal motion is capable of disorienting atoms in domains, as a result of which the ferromagnet turns into a paramagnet.
The flux of magnetic induction through a certain surface S is equal to the number of induction lines penetrating this surface:
![]() (5)
(5)
Unit of measurement B – Tesla, F-Weber.