Events that happen in reality or in our imagination can be divided into 3 groups. These are certain events that are sure to happen, impossible events and random events. Probability theory studies random events, i.e. events that may or may not happen. This article will briefly present the theory of probability formulas and examples of solving problems in probability theory, which will be in task 4 of the Unified State Exam in mathematics (profile level).
Why do we need probability theory?
Historically, the need to study these problems arose in the 17th century in connection with the development and professionalization gambling and the emergence of casinos. This was a real phenomenon that required its own study and research.
Playing cards, dice, and roulette created situations where any of a finite number of equally possible events could occur. There was a need to give numerical estimates of the possibility of the occurrence of a particular event.
In the 20th century, it turned out that this seemingly frivolous science plays important role in the knowledge of fundamental processes occurring in the microcosm. Was created modern theory probabilities.
Basic concepts of probability theory
The object of study of probability theory is events and their probabilities. If an event is complex, then it can be broken down into simple components, the probabilities of which are easy to find.
The sum of events A and B is called event C, which consists in the fact that either event A, or event B, or events A and B occurred simultaneously.
The product of events A and B is an event C, which means that both event A and event B occurred.
Events A and B are called incompatible if they cannot occur simultaneously.
An event A is called impossible if it cannot happen. Such an event is indicated by the symbol.
An event A is called certain if it is sure to happen. Such an event is indicated by the symbol.
Let each event A be associated with a number P(A). This number P(A) is called the probability of event A if the following conditions are met with this correspondence.
An important special case is the situation when there are equally probable elementary outcomes, and arbitrary of these outcomes form events A. In this case, the probability can be entered using the formula. Probability introduced in this way is called classical probability. It can be proven that in this case properties 1-4 are satisfied.
Probability theory problems that appear on the Unified State Examination in mathematics are mainly related to classical probability. Such tasks can be very simple. Particularly simple are problems in probability theory in demo options. It is easy to calculate the number of favorable outcomes; the number of all outcomes is written right in the condition.

We get the answer using the formula.
An example of a problem from the Unified State Examination in mathematics on determining probability
There are 20 pies on the table - 5 with cabbage, 7 with apples and 8 with rice. Marina wants to take the pie. What is the probability that she will take the rice cake?
Solution.
There are 20 equally probable elementary outcomes, that is, Marina can take any of the 20 pies. But we need to estimate the probability that Marina will take the rice pie, that is, where A is the choice of the rice pie. This means that the number of favorable outcomes (choices of pies with rice) is only 8. Then the probability will be determined by the formula:
![]()
Independent, Opposite and Arbitrary Events
However, in open jar More complex tasks began to be encountered. Therefore, let us draw the reader’s attention to other issues studied in probability theory.
Events A and B are said to be independent if the probability of each does not depend on whether the other event occurs.
Event B is that event A did not happen, i.e. event B is opposite to event A. The probability of the opposite event is equal to one minus the probability of the direct event, i.e. .
Probability addition and multiplication theorems, formulas
For arbitrary events A and B, the probability of the sum of these events is equal to the sum of their probabilities without the probability of their joint event, i.e. .
For independent events A and B, the probability of the occurrence of these events is equal to the product of their probabilities, i.e. in this case .
The last 2 statements are called the theorems of addition and multiplication of probabilities.
Counting the number of outcomes is not always so simple. In some cases it is necessary to use combinatorics formulas. The most important thing is to count the number of events that satisfy certain conditions. Sometimes these kinds of calculations can become independent tasks.
In how many ways can 6 students be seated in 6 empty seats? The first student will take any of the 6 places. Each of these options corresponds to 5 ways for the second student to take a place. There are 4 free places left for the third student, 3 for the fourth, 2 for the fifth, and the sixth will take the only remaining place. To find the number of all options, you need to find the product, which is denoted by the symbol 6! and reads "six factorial".
In the general case, the answer to this question is given by the formula for the number of permutations of n elements. In our case.
Let us now consider another case with our students. In how many ways can 2 students be seated in 6 empty seats? The first student will take any of the 6 places. Each of these options corresponds to 5 ways for the second student to take a place. To find the number of all options, you need to find the product.
In general, the answer to this question is given by the formula for the number of placements of n elements over k elements
In our case .
And the last case in this series. In how many ways can you choose three students out of 6? The first student can be selected in 6 ways, the second - in 5 ways, the third - in four ways. But among these options, the same three students appear 6 times. To find the number of all options, you need to calculate the value: . In general, the answer to this question is given by the formula for the number of combinations of elements by element:
In our case .
Examples of solving problems from the Unified State Exam in mathematics to determine probability
Task 1. From the collection edited by. Yashchenko.
There are 30 pies on the plate: 3 with meat, 18 with cabbage and 9 with cherries. Sasha chooses one pie at random. Find the probability that he ends up with a cherry.
![]() .
.
Answer: 0.3.
Task 2. From the collection edited by. Yashchenko.
In each batch of 1000 light bulbs, on average, 20 are defective. Find the probability that a light bulb taken at random from a batch will be working.
Solution: The number of working light bulbs is 1000-20=980. Then the probability that a light bulb taken at random from a batch will be working:
![]()
Answer: 0.98.
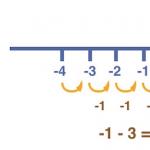
The probability that student U will solve more than 9 problems correctly during a math test is 0.67. The probability that U. will correctly solve more than 8 problems is 0.73. Find the probability that U will solve exactly 9 problems correctly.
If we imagine a number line and mark points 8 and 9 on it, then we will see that the condition “U. will solve exactly 9 problems correctly” is included in the condition “U. will solve more than 8 problems correctly”, but does not apply to the condition “U. will solve more than 9 problems correctly.”
However, the condition “U. will solve more than 9 problems correctly” is contained in the condition “U. will solve more than 8 problems correctly.” Thus, if we designate events: “U. will solve exactly 9 problems correctly" - through A, "U. will solve more than 8 problems correctly" - through B, "U. will correctly solve more than 9 problems” through C. That solution will look like this:
Answer: 0.06.
In a geometry exam, a student answers one question from a list of exam questions. The probability that this is a Trigonometry question is 0.2. The probability that this is a question on External Angles is 0.15. There are no questions that simultaneously relate to these two topics. Find the probability that a student will get a question on one of these two topics in the exam.
Let's think about what events we have. We are given two incompatible events. That is, either the question will relate to the topic “Trigonometry” or to the topic “External angles”. According to the probability theorem, the probability of incompatible events is equal to the sum of the probabilities of each event, we must find the sum of the probabilities of these events, that is:
Answer: 0.35.
The room is illuminated by a lantern with three lamps. The probability of one lamp burning out within a year is 0.29. Find the probability that at least one lamp will not burn out during the year.
Let's consider possible events. We have three light bulbs, each of which may or may not burn out independently of any other light bulb. These are independent events.
Then we will indicate the options for such events. Let's use the following notations: - the light bulb is on, - the light bulb is burnt out. And right next to it we will calculate the probability of the event. For example, the probability of an event in which three independent events “the light bulb is burned out”, “the light bulb is on”, “the light bulb is on” occurred: , where the probability of the event “the light bulb is on” is calculated as the probability of the event opposite to the event “the light bulb is not on”, namely: .
Note that there are only 7 incompatible events favorable to us. The probability of such events is equal to the sum of the probabilities of each of the events: .
Answer: 0.975608.
You can see another problem in the figure:

Thus, we have understood what the theory of probability is, formulas and examples of solving problems that you may encounter in the Unified State Exam version.
I’m generally very weak in such problems, so I tried to find the answer on the Internet, but it turned out that different answers were reported in different places. Let us try to figure out which one is correct. Here's the actual problem:
This unusual question was coined by mathematician Raymond Johnson:
If you choose an answer at random, what is the probability that it will be correct?
a) 25%
b) 50%
c) 60%
d) 25%
Here are the explanations and answer options available on the Internet:
Option answer - 0%
The correct answer is 0%, i.e. it is not offered among the results.
Let us explain: the possible number of correct answers is from 0 to 4, which means that the probability of randomly choosing the correct one should be 0, 25, 50, 75 or 100%. This automatically excludes option c) (there cannot be a 60% probability).
Further, since a) and d) are the same, they are either both true or both false.
So, we have 4 mutually exclusive answer options:
1: a), b) and d) are the correct answers.
2: a) and d) are the correct answers.
3: b) is the correct answer.
4: There is no right answer.
The first option is impossible, since the probability cannot be both 25% and 50% at the same time.
The second option is impossible because if 2 answers are correct, then the probability of selection should be 50%, not 25%.
The same with the third option: if only 1 option is correct, then the probability of choosing it is 25%, not 50% (as stated in answer b)).
So, that leaves option 4: there is no right answer. Therefore, the probability of choosing the correct answer is 0%.
Option answer 37.5%:
There are 3 possible cases when guessing the answer. 1 - chose 25% and guessed right. 2 - chose 50% and guessed right. 3 - chose 60% and guessed right.
1) The chance that you will choose 25% = 1/2. At the same time, the chance that you will guess these 25% is also 1/2.
The final probability of the case is 1/2 * 1/2 = 1/4.
2) The chance that you will choose 50% = 1/4. At the same time, the chance that you will guess these 50% is also 1/4.
3) The chance that you will choose 60% = 1/4. At the same time, the chance that you will guess these 60% is also 1/4.
The final probability of the case is 1/4 * 1/4 = 1/16.
We sum up the final probabilities for all 3 cases, we get 3/8, or 37.5%.
Option answer - 50%
It will turn out to be one and two
1) First, let's determine what the probability of each answer is. Everything is simple here - according to logic, the probability that we will choose one of the four answer options will be 1/4, that is, 0.25
2) Now let’s calculate the probability of hitting the answer options with the number 25%. If we take into account that the events are not compatible, that is, the appearance of one excludes the appearance of the other, then we can use the sum of probabilities (the probability that we will answer 1 or 4, since they contain the 25% we need), that is, 25% + 25% = 50% percent.
As a result, the correct answer is b)
Possible answer: recursion
I explain: out of 4 options, 1 is at random, that is, 25%, but there are 2 such options, so we multiply by 2, so it becomes 50%, but this option is 1, so we divide by 2 and we get 25%, but there are 2 such options, so we multiply by 2, it became 50%, but this option is 1, so we divide by 2 and get 25%, but there are 2 such options, so we multiply by 2, it becomes 50%, but this option is 1, so we divide by 2 and we get 25%, but such There are 2 options, so we multiply by 2, it becomes 50%, but this option is 1, so we divide by 2 and we get 25%, but there are 2 such options, so we multiply by 2, it becomes 50%, but this option is 1, so we divide by 2 and we get 25%, but there are 2 such options, so we multiply by 2, it becomes 50%, but this option is 1, so we divide by 2 and we get 25%...
When a coin is tossed, we can say that it will land heads up, or probability this is 1/2. Of course, this does not mean that if a coin is tossed 10 times, it will necessarily land on heads 5 times. If the coin is "fair" and if it is tossed many times, then heads will land very close half the time. Thus, there are two types of probabilities: experimental And theoretical .
Experimental and theoretical probability
If you toss a coin a large number of times - say 1000 - and count the number of times heads are thrown, we can determine the probability of heads being thrown. If heads are thrown 503 times, we can calculate the probability of it landing:
503/1000, or 0.503.
This experimental determination of probability. This definition of probability comes from observation and study of data and is quite common and very useful. Here, for example, are some probabilities that were determined experimentally:
1. The probability that a woman will develop breast cancer is 1/11.
2. If you kiss someone who has a cold, then the probability that you will also get a cold is 0.07.
3. A person who has just been released from prison has an 80% chance of returning to prison.
If we consider tossing a coin and taking into account that it is just as likely that it will come up heads or tails, we can calculate the probability of getting heads: 1/2. This is theoretical definition probabilities. Here are some other probabilities that have been determined theoretically using mathematics:
1. If there are 30 people in a room, the probability that two of them have the same birthday (excluding year) is 0.706.
2. During a trip, you meet someone, and during the conversation you discover that you have a mutual friend. Typical reaction: “This can’t be!” In fact, this phrase is not suitable, because the probability of such an event is quite high - just over 22%.
Thus, experimental probabilities are determined through observation and data collection. Theoretical probabilities are determined through mathematical reasoning. Examples of experimental and theoretical probabilities, such as those discussed above, and especially those that we do not expect, lead us to the importance of studying probability. You may ask, "What is true probability?" In fact, there is no such thing. Probabilities within certain limits can be determined experimentally. They may or may not coincide with the probabilities that we obtain theoretically. There are situations in which it is much easier to determine one type of probability than another. For example, it would be sufficient to find the probability of catching a cold using theoretical probability.
Calculation of experimental probabilities
Let us first consider the experimental definition of probability. The basic principle we use to calculate such probabilities is as follows.
Principle P (experimental)
If in an experiment in which n observations are made, a situation or event E occurs m times in n observations, then the experimental probability of the event is said to be P (E) = m/n.
Example 1 Sociological survey. An experimental study was conducted to determine the number of left-handed people, right-handed people and people whose both hands are equally developed. The results are shown in the graph.
a) Determine the probability that the person is right-handed.
b) Determine the probability that the person is left-handed.
c) Determine the probability that a person is equally fluent in both hands.
d) Most Professional Bowling Association tournaments are limited to 120 players. Based on the data from this experiment, how many players could be left-handed?
Solution
a)The number of people who are right-handed is 82, the number of left-handers is 17, and the number of those who are equally fluent in both hands is 1. The total number of observations is 100. Thus, the probability that a person is right-handed is P
P = 82/100, or 0.82, or 82%.
b) The probability that a person is left-handed is P, where
P = 17/100, or 0.17, or 17%.
c) The probability that a person is equally fluent in both hands is P, where
P = 1/100, or 0.01, or 1%.
d) 120 bowlers, and from (b) we can expect that 17% are left-handed. From here
17% of 120 = 0.17.120 = 20.4,
that is, we can expect about 20 players to be left-handed.
Example 2 Quality control
. It is very important for a manufacturer to maintain the quality of its products at high level. In fact, companies hire quality control inspectors to ensure this process. The goal is to produce the minimum possible number of defective products. But since the company produces thousands of products every day, it cannot afford to test every product to determine whether it is defective or not. To find out what percentage of products are defective, the company tests far fewer products.
Ministry Agriculture The US requires that 80% of the seeds sold by growers must germinate. To determine the quality of the seeds that an agricultural company produces, 500 seeds from those that were produced are planted. After this, it was calculated that 417 seeds sprouted.
a) What is the probability that the seed will germinate?
b) Do the seeds meet government standards?
Solution a) We know that out of 500 seeds that were planted, 417 sprouted. Probability of seed germination P, and
P = 417/500 = 0.834, or 83.4%.
b) Since the percentage of seeds germinated has exceeded 80% as required, the seeds meet government standards.
Example 3 Television ratings. According to statistics, there are 105,500,000 households with televisions in the United States. Every week, information about viewing programs is collected and processed. In one week, 7,815,000 households tuned in to the hit comedy series "Everybody Loves Raymond" on CBS and 8,302,000 households tuned in to the hit series "Law & Order" on NBC (Source: Nielsen Media Research). What is the probability that one household's TV is tuned to "Everybody Loves Raymond" during a given week? to "Law & Order"?
Solution The probability that the TV in one household is tuned to "Everybody Loves Raymond" is P, and
P = 7,815,000/105,500,000 ≈ 0.074 ≈ 7.4%.
The chance that the household's TV was tuned to Law & Order is P, and
P = 8,302,000/105,500,000 ≈ 0.079 ≈ 7.9%.
These percentages are called ratings.
Theoretical probability
Suppose we are conducting an experiment, such as throwing a coin or darts, drawing a card from a deck, or testing products for quality on an assembly line. Each possible result of such an experiment is called Exodus . The set of all possible outcomes is called outcome space . Event it is a set of outcomes, that is, a subset of the space of outcomes.
Example 4 Throwing darts. Suppose that in a dart throwing experiment, a dart hits a target. Find each of the following:
b) Outcome space
Solution
a) The outcomes are: hitting black (B), hitting red (R) and hitting white (B).
b) The space of outcomes is (hitting black, hitting red, hitting white), which can be written simply as (H, K, B).
Example 5 Throwing dice.
A die is a cube with six sides, each with one to six dots on it. 
Suppose we are throwing a die. Find
a) Outcomes
b) Outcome space
Solution
a) Outcomes: 1, 2, 3, 4, 5, 6.
b) Outcome space (1, 2, 3, 4, 5, 6).
We denote the probability that an event E occurs as P(E). For example, “the coin will land on heads” can be denoted by H. Then P(H) represents the probability that the coin will land on heads. When all outcomes of an experiment have the same probability of occurring, they are said to be equally likely. To see the differences between events that are equally likely and events that are not, consider the target shown below. 
For target A, the events of hitting black, red and white are equally probable, since the black, red and white sectors are the same. However, for target B, the zones with these colors are not the same, that is, hitting them is not equally probable.
Principle P (Theoretical)
If an event E can happen in m ways out of n possible equally probable outcomes from the outcome space S, then theoretical probability
events, P(E) is
P(E) = m/n.
Example 6 What is the probability of rolling a die to get a 3?
Solution There are 6 equally probable outcomes on a dice and there is only one possibility of rolling the number 3. Then the probability P will be P(3) = 1/6.
Example 7 What is the probability of rolling an even number on a die?
Solution The event is the throwing of an even number. This can happen in 3 ways (if you roll a 2, 4 or 6). The number of equally probable outcomes is 6. Then the probability P(even) = 3/6, or 1/2.
We will use a number of examples involving a standard 52 card deck. This deck consists of the cards shown in the figure below. 
Example 8 What is the probability of drawing an Ace from a well-shuffled deck of cards?
Solution There are 52 outcomes (the number of cards in the deck), they are equally likely (if the deck is well shuffled), and there are 4 ways to draw an Ace, so according to the P principle, the probability
P(draw an ace) = 4/52, or 1/13.
Example 9 Suppose we choose, without looking, one ball from a bag with 3 red balls and 4 green balls. What is the probability of choosing a red ball?
Solution There are 7 equally probable outcomes of drawing any ball, and since the number of ways to draw a red ball is 3, we get
P(red ball selection) = 3/7.
The following statements are results from Principle P.
Properties of Probability
a) If event E cannot happen, then P(E) = 0.
b) If event E is certain to happen then P(E) = 1.
c) The probability that event E will occur is a number from 0 to 1: 0 ≤ P(E) ≤ 1.
For example, in a coin toss, the event that the coin lands on its edge has zero probability. The probability that a coin is either heads or tails has a probability of 1.
Example 10 Let's assume that 2 cards are drawn from a 52-card deck. What is the probability that both of them are peaks?
Solution The number n of ways to draw 2 cards from a well-shuffled deck of 52 cards is 52 C 2 . Since 13 of the 52 cards are spades, the number of ways m to draw 2 spades is 13 C 2 . Then,
P(pulling 2 peaks) = m/n = 13 C 2 / 52 C 2 = 78/1326 = 1/17.
Example 11 Suppose 3 people are randomly selected from a group of 6 men and 4 women. What is the probability that 1 man and 2 women will be selected?
Solution The number of ways to select three people from a group of 10 people is 10 C 3. One man can be chosen in 6 C 1 ways, and 2 women can be chosen in 4 C 2 ways. According to the fundamental principle of counting, the number of ways to choose 1 man and 2 women is 6 C 1. 4 C 2 . Then, the probability that 1 man and 2 women will be selected is
P = 6 C 1 . 4 C 2 / 10 C 3 = 3/10.
Example 12 Throwing dice. What is the probability of rolling a total of 8 on two dice?
Solution Each dice has 6 possible outcomes. The outcomes are doubled, meaning there are 6.6 or 36 possible ways in which the numbers on the two dice can appear. (It’s better if the cubes are different, say one is red and the other is blue - this will help visualize the result.) 
The pairs of numbers that add up to 8 are shown in the figure below. There are 5 possible ways to obtain a sum equal to 8, hence the probability is 5/36.
The probability of an event quantitatively characterizes the possibility (chance) of this event occurring during a random experiment. In this section, we begin to study the possibilities provided by probability theory for the comparative analysis of situations arising from various combinations of equally probable events.
Let's imagine that we are conducting an experiment with space from n elementary outcomes that equally probable. The elementary outcomes are incompatible events (recall that incompatible events are those that cannot happen at the same time), so the probability of each of them is 1/n. Let's say we are interested in event A, which occurs only when favorable elementary outcomes, number of last m(m< n). Тогда, согласно classical definition, the probability of such an event:
R( A)=m/n.
For any event A the following inequality holds: 0 < P(A) <1.
Example 1.The lottery consists of 1000 tickets, including 200 winning ones. One ticket out of 1000 is drawn at random. What is the probability that this ticket is a winner?
Solution: There are 1000 different outcomes in this example (n=1000). The event A we are interested in includes 200 outcomes (m=200). Thus,
Example 2. A box contains 200 white, 100 red and 50 green balls. One ball is drawn at random. Why equal to the probability of getting Is the ball white, red or green?
Solution: Let's consider the events:
A = (they took out a white ball),
B = (they took out a red ball),
C = (they took out a green ball).
N=350, then
![]()
![]()
![]()
Example 3. The dice are thrown. What are the probabilities of the following events:
A = (the side with 6 points fell out),
B = (the side with an even number of points fell),
C=(the side with the number of points divisible by 3 fell)?
Solution: n = 6. Event A is favored by one outcome, event B by three outcomes, event C by two outcomes. Thus,
![]()
![]()
Sometimes in problems the number of elementary outcomes is so large that it is not possible to write them all down. Therefore, formulas from combinatorics are used (see §2).
Example 4. Three are drawn from a deck of 36 cards. What is the probability that among the cards drawn there are no tens?
Solution: In this example, the elementary outcome is a random set of three cards. The total number of elementary outcomes is N=C 36 3; we consider the elementary outcomes to be equally possible. Favorable outcomes (the number of possible sets of three cards from the same deck, but without tens)
m=C 32 3 . Thus, the probability of event A (3 cards out of 36 are drawn and there are no tens among them):
![]()
Self-test tasks
1. Two dice are thrown at the same time. Find the probabilities of the following events: A-sum of points drawn is 8; B-product of the rolled points is 8.
Total number of outcomes: n=6x6=36, number of favorable outcomes of event A ,, , , m=5, desired probability p=m/n=5/36. For event B, favorable outcomes: , , i.e. m=2 and the desired probability p=m/n=2/36=1/18.
2. In the envelope, among 100 photographs, there is one wanted one. 10 cards are drawn at random from the envelope. Find the probability that the wanted one will be among them.
Let's divide all 100 photos equally into 10 envelopes. The probability of taking an envelope with the desired photo is p=1/10.
3. While dialing a phone number, the subscriber forgot the last three digits and, remembering only that these digits were different, dialed them at random. Find the probability that the number is dialed correctly.
In the first place of this three-digit number there can be any of the 10 digits from 0 to 9, in the second place only 9, because the numbers are not repeated on the third 8, in total n=10x9x8=720, this is the total number of outcomes, there is one favorable outcome m=1, so p=m/n=1/720.
From a practical point of view, probability of an event is the ratio of the number of those observations in which the event in question occurred to the total number of observations. This interpretation is acceptable in the case of a sufficiently large number of observations or experiments. For example, if about half of the people you meet on the street are women, then you can say that the probability that the person you meet on the street will be a woman is 1/2. In other words, an estimate of the probability of an event can be the frequency of its occurrence in a long series of independent repetitions of a random experiment.
Probability in mathematics
In the modern mathematical approach, classical (that is, not quantum) probability is given by the Kolmogorov axiomatics. Probability is a measure P, which is defined on the set X, called probability space. This measure must have the following properties:
From these conditions it follows that the probability measure P also has the property additivity: if sets A 1 and A 2 do not intersect, then . To prove you need to put everything A 3 , A 4 , ... equal to the empty set and apply the property of countable additivity.
The probability measure may not be defined for all subsets of the set X. It is enough to define it on a sigma algebra, consisting of some subsets of the set X. In this case, random events are defined as measurable subsets of space X, that is, as elements of sigma algebra.
Probability sense
When we find that the reasons for some possible fact actually occurring outweigh the contrary reasons, we consider that fact probable, otherwise - incredible. This preponderance of positive bases over negative ones, and vice versa, can represent an indefinite set of degrees, as a result of which probability(And improbability) It happens more or less .
Complex individual facts do not allow for an exact calculation of the degrees of their probability, but even here it is important to establish some large subdivisions. So, for example, in the legal field, when a personal fact subject to trial is established on the basis of testimony, it always remains, strictly speaking, only probable, and it is necessary to know how significant this probability is; in Roman law, a quadruple division was adopted here: probatio plena(where the probability practically turns into reliability), Further - probatio minus plena, then - probatio semiplena major and finally probatio semiplena minor .
In addition to the question of the probability of the case, the question may arise, both in the field of law and in the moral field (with a certain ethical point of view), of how likely it is that a given particular fact constitutes a violation of the general law. This question, which serves as the main motive in the religious jurisprudence of the Talmud, also gave rise to very complex systematic constructions and a huge literature, dogmatic and polemical, in Roman Catholic moral theology (especially from the end of the 16th century) (see Probabilism).
The concept of probability allows for a certain numerical expression when applied only to such facts that are part of certain homogeneous series. So (in the simplest example), when someone throws a coin a hundred times in a row, we find here one general or large series (the sum of all falls of the coin), consisting of two private or smaller, in this case numerically equal, series (falls " heads" and falls "tails"); The probability that this time the coin will land heads, that is, that this new member of the general series will belong to this of the two smaller series, is equal to the fraction expressing the numerical relationship between this small series and the larger one, namely 1/2, that is, the same probability belongs to one or the other of two particular series. In less simple examples, the conclusion cannot be deduced directly from the data of the problem itself, but requires prior induction. So, for example, the question is: what is the probability for a given newborn to live to be 80 years old? Here there must be a general, or large, series of a certain number of people born in similar conditions and dying at different ages (this number must be large enough to eliminate random deviations, and small enough to maintain the homogeneity of the series, for for a person, born, for example, in St. Petersburg into a wealthy, cultured family, the entire million-strong population of the city, a significant part of which consists of people from various groups who can die prematurely - soldiers, journalists, workers in dangerous professions - represents a group too heterogeneous for a real determination of probability) ; let this general series consist of ten thousand human lives; it includes smaller series representing the number of people surviving to a particular age; one of these smaller series represents the number of people living to age 80. But it is impossible to determine the number of this smaller series (like all others) a priori; this is done purely inductively, through statistics. Suppose statistical studies have established that out of 10,000 middle-class St. Petersburg residents, only 45 live to be 80; Thus, this smaller series is related to the larger one as 45 is to 10,000, and the probability for a given person to belong to this smaller series, that is, to live to be 80 years old, is expressed as a fraction of 0.0045. The study of probability from a mathematical point of view constitutes a special discipline - probability theory.
see also
Notes
Literature
Wikimedia Foundation. 2010.
Synonyms:Antonyms:
See what “Probability” is in other dictionaries:
General scientific and philosophical. a category denoting the quantitative degree of possibility of the occurrence of mass random events under fixed observation conditions, characterizing the stability of their relative frequencies. In logic, semantic degree... ... Philosophical Encyclopedia
PROBABILITY, a number in the range from zero to one inclusive, representing the possibility of a given event occurring. The probability of an event is defined as the ratio of the number of chances that an event can occur to the total number of possible... ... Scientific and technical encyclopedic dictionary
In all likelihood.. Dictionary of Russian synonyms and similar expressions. under. ed. N. Abramova, M.: Russian Dictionaries, 1999. probability possibility, likelihood, chance, objective possibility, maza, admissibility, risk. Ant. impossibility... ... Synonym dictionary
probability- A measure that an event is likely to occur. Note The mathematical definition of probability is: “a real number between 0 and 1 that is associated with a random event.” The number may reflect the relative frequency in a series of observations... ... Technical Translator's Guide
Probability- “a mathematical, numerical characteristic of the degree of possibility of the occurrence of any event in certain specific conditions that can be repeated an unlimited number of times.” Based on this classic... ... Economic and mathematical dictionary
- (probability) The possibility of the occurrence of an event or a certain result. It can be presented in the form of a scale with divisions from 0 to 1. If the probability of an event is zero, its occurrence is impossible. With a probability equal to 1, the onset of... Dictionary of business terms