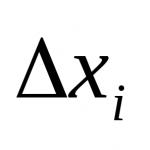Throughout the example, we will use fictitious information so that the reader can make the necessary transformations on his own.
So, let’s say, in the course of research, we studied the effect of drug A on the content of substance B (in mmol/g) in tissue C and the concentration of substance D in the blood (in mmol/l) in patients divided according to some criterion E into 3 groups of equal volume (n = 10). The results of such a fictitious study are shown in the table:
| Content of substance B, mmol/g |
Substance D, mmol/l |
||||||
|---|---|---|---|---|---|---|---|
|
increase in concentration |
|||||||
We would like to warn you that we consider samples of size 10 for ease of data presentation and calculations; in practice, such a sample size is usually not enough to form a statistical conclusion.
As an example, consider the data in the 1st column of the table.
Descriptive Statistics
Sample mean
The arithmetic mean, often simply called the "mean", is obtained by adding all the values and dividing that sum by the number of values in the set. This can be shown using an algebraic formula. A set of n observations of a variable x can be represented as x 1 , x 2 , x 3 , ..., x n
The formula for determining the arithmetic mean of observations (pronounced “X with a line”):
= (X 1 + X 2 + ... + X n) / n
= (12 + 13 + 14 + 15 + 14 + 13 + 13 + 10 + 11 + 16) / 10 = 13,1;
Sample variance
One way to measure the dispersion of data is to determine the degree to which each observation deviates from the arithmetic mean. Obviously, the greater the deviation, the greater the variability, variability of observations. However, we cannot use the average of these deviations as a measure of dispersion, because positive deviations compensate for negative deviations (their sum is zero). To solve this problem, we square each deviation and find the average of the squared deviations; this quantity is called variation, or dispersion. Let's take n observations x 1, x 2, x 3, ..., x n, average which is equal to. Calculating the variance this, usually referred to ass2,these observations:

The sample variance of this indicator is s 2 = 3.2.
Standard deviation
Standard (mean square) deviation is positive Square root from dispersion. Using n observations as an example, it looks like this:

We can think of standard deviation as a kind of average deviation of observations from the mean. It is calculated in the same units (dimensions) as the original data.
s = sqrt (s 2) = sqrt (3,2) = 1.79.
The coefficient of variation
If you divide the standard deviation by the arithmetic mean and express the result as a percentage, you get the coefficient of variation.
CV = (1.79 / 13.1) * 100% = 13.7
Sample mean error
1.79/sqrt(10) = 0.57;
Student's t coefficient (one-sample t-test)
Used to test the hypothesis about the difference between the average value and some known value m

The number of degrees of freedom is calculated as f=n-1.
In this case, the confidence interval for the mean is between the boundaries of 11.87 and 14.39.
For the 95% confidence level m=11.87 or m=14.39, that is= |13.1-11.82| = |13.1-14.38| = 1.28
Accordingly, in this case, for the number of degrees of freedom f = 10 - 1 = 9 and the 95% confidence level t = 2.26.
Dialog Basic Statistics and Tables
In the module Basic statistics and tables let's choose Descriptive Statistics.
A dialog box will open Descriptive Statistics.
In field Variables let's choose Group 1.
Pressing OK, we obtain tables of results with descriptive statistics of the selected variables.
A dialog box will open One-sample t-test.
Suppose we know that the average content of substance B in tissue C is 11.
The table of results with descriptive statistics and Student's t-test is as follows:
We had to reject the hypothesis that the average content of substance B in tissue C is 11.
Since the calculated value of the criterion is greater than the tabulated value (2.26), the null hypothesis is rejected at the selected significance level, and the differences between the sample and the known value are considered statistically significant. Thus, the conclusion about the existence of differences made using the Student's test is confirmed using this method.
Testing a statistical hypothesis allows us to draw a strict conclusion about the characteristics population based on sample data. There are different hypotheses. One of them is the hypothesis about the average (mathematical expectation). Its essence is to draw a correct conclusion, based only on the available sample, about where the general average may or may not be located (we will never know the exact truth, but we can narrow down the search).
The general approach to testing hypotheses has been described, so let's get straight to the point. Let us first assume that the sample is drawn from a normal population of random variables X with general average μ and variance σ 2(I know, I know that this doesn’t happen, but don’t interrupt me!). The arithmetic mean of this sample is obviously itself a random variable. If you extract many such samples and calculate their averages, then they will also have a mathematical expectation μ And
Then random value
![]()
The question arises: will the general average with a 95% probability be within ±1.96? s x̅. In other words, are the distributions of random variables
equivalent.
This question was first posed (and solved) by a chemist who worked at the Guinness beer factory in Dublin (Ireland). The chemist's name was William Seely Gosset and he took samples of beer for testing. chemical analysis. At some point, apparently, William began to be tormented by vague doubts about the distribution of averages. It turned out to be a little more smeared than a normal distribution should be.
Having collected the mathematical basis and calculated the values of the distribution function he discovered, the Dublin chemist William Gosset wrote a note that was published in the March 1908 issue of the Biometrics magazine (editor-in-chief - Karl Pearson). Because Guinness strictly forbade giving away brewing secrets; Gossett signed with the pseudonym Student.
Despite the fact that K. Pearson had already invented the distribution, the general idea of normality still dominated. No one was going to think that the distribution of sample scores might not be normal. Therefore, W. Gosset’s article remained practically unnoticed and forgotten. And only Ronald Fisher appreciated Gosset's discovery. Fischer used the new distribution in his work and gave it the name Student's t-distribution. The criterion for testing hypotheses, accordingly, became Student's t-test. This is how a “revolution” occurred in statistics, which stepped into the era of analysis of sample data. It was short excursion into history.
Let's see what W. Gosset could see. Let's generate 20 thousand normal samples from 6 observations with an average ( X̅) 50 and standard deviation ( σ ) 10. Then we normalize the sample means using general variance:
![]()
We will group the resulting 20 thousand averages into intervals of length 0.1 and calculate the frequencies. Let us depict on the diagram the actual (Norm) and theoretical (ENorm) frequency distribution of sample means.

The points (observed frequencies) practically coincide with the line (theoretical frequencies). This is understandable, because the data is taken from the same general population, and the differences are only sampling errors.
Let's conduct a new experiment. We normalize the averages using sample variance.
![]()
Let's count the frequencies again and plot them on the diagram in the form of points, leaving a standard normal distribution line for comparison. Let us denote the empirical frequency of the averages, say, by the letter t.

It can be seen that the distributions this time do not coincide very much. Close, yes, but not the same. The tails have become more “heavy”.
Gosset-Student did not have the latest version of MS Excel, but this is exactly the effect he noticed. Why does this happen? The explanation is that the random variable
depends not only on the sampling error (numerator), but also on the standard error of the mean (denominator), which is also a random variable.
Let's take a little look at what distribution such a random variable should have. First you will have to remember (or learn) something from mathematical statistics. There is Fisher's theorem, which states that in a sample from a normal distribution:
1. medium X̅ and sample variance s 2 are independent quantities;
2. the ratio of sample and population variance, multiplied by the number of degrees of freedom, has a distribution χ 2(chi-square) with the same number of degrees of freedom, i.e.
Where k– number of degrees of freedom (in English degrees of freedom (d.f.))
Many other results in the statistics of normal models are based on this law.
Let's return to the distribution of the average. Divide the numerator and denominator of the expression
on σ X̅. We get
The numerator is a standard normal random variable (we denote ξ (xi)). Let us express the denominator from Fisher's theorem.
Then the original expression will take the form
This is what is in general view(Student ratio). You can derive its distribution function directly, because the distributions of both random variables in this expression are known. Let's leave this pleasure to the mathematicians.
The Student t-distribution function has a formula that is quite difficult to understand, so there is no point in analyzing it. Nobody uses it anyway, because... probabilities are given in special tables of Student distributions (sometimes called tables of Student coefficients), or are included in PC formulas.
So, armed with this new knowledge, you can understand the official definition of the Student distribution.
A random variable subject to the Student distribution with k degrees of freedom is the ratio of independent random variables
Where ξ distributed according to the standard normal law, and χ 2 k obeys distribution χ 2 c k degrees of freedom.
Thus, the Student's t test formula for the arithmetic mean
There is special case student relationship
From the formula and definition it follows that the distribution of Student’s t-test depends only on the number of degrees of freedom.

At k> 30 t-test practically does not differ from the standard normal distribution.
Unlike chi-square, the t-test can be one-tailed or two-tailed. Usually they use two-sided, assuming that the deviation can occur in both directions from the average. But if the problem condition allows deviation only in one direction, then it is reasonable to use a one-sided criterion. This increases the power slightly, because... at a fixed significance level, the critical value approaches zero slightly.
Conditions for using Student's t-test
Despite the fact that Student’s discovery at one time revolutionized statistics, the t-test is still quite limited in its application possibilities, because itself comes from the assumption of a normal distribution of the original data. If the data is not normal (which is usually the case), then the t-test will no longer have a Student distribution. However, due to the action of the central limit theorem, the average even for abnormal data quickly acquires a bell-shaped distribution.
Consider, for example, data that is clearly skewed to the right, such as a chi-square distribution with 5 degrees of freedom.

Now let’s create 20 thousand samples and observe how the distribution of averages changes depending on their volume.

The difference is quite noticeable in small samples of up to 15-20 observations. But then it quickly disappears. Thus, the non-normality of the distribution is, of course, not good, but not critical.
Most of all, the t-test is “afraid” of outliers, i.e. abnormal deviations. Let's take 20 thousand normal samples of 15 observations each and add one random outlier to some of them.

The picture turns out to be bleak. The actual frequencies of the averages are very different from the theoretical ones. Using the t-distribution in such a situation becomes a very risky undertaking.
So, in not very small samples (from 15 observations), the t-test is relatively resistant to non-normal distribution of the original data. But outliers in the data greatly distort the distribution of the t-test, which, in turn, can lead to errors in statistical inference, so anomalous observations should be eliminated. Often, all values that fall within ±2 standard deviations from the mean are removed from the sample.
An example of testing a hypothesis about mathematical expectation using Student's t-test in MS Excel
Excel has several functions related to the t-distribution. Let's look at them.
STUDENT.DIST – “classical” left-sided Student t-distribution. The input is the t-criterion value, the number of degrees of freedom, and an option (0 or 1) that determines what needs to be calculated: density or function value. At the output we obtain, respectively, the density or the probability that the random variable will be less than the t-criterion specified in the argument, i.e. left-tailed p-value.
STUDENT.DIST.2X – two-way distribution. The argument is the absolute value (modulo) of the t-test and the number of degrees of freedom. As a result, we get the probability of getting this or more more value t-test (modulo), i.e. actual significance level (p-value).
STUDENT.DIST.PH – right-sided t-distribution. So, 1-STUDENT.DIST(2;5;1) = STUDENT.DIST.PH(2;5) = 0.05097. If the t-test is positive, then the resulting probability is the p-value.
STUDENT.OBR – used to calculate left-handed reciprocal value t-distributions. The argument is the probability and the number of degrees of freedom. At the output we obtain the t-criterion value corresponding to this probability. The probability count is on the left. Therefore, the left tail requires the significance level itself α , and for the right one 1 - α .
STUDENT.OBR.2X – the inverse value for the two-sided Student distribution, i.e. t-test value (modulo). The significance level is also supplied to the input α . Only this time the counting is carried out from both sides simultaneously, so the probability is distributed into two tails. So, STUDENT.ARV(1-0.025;5) = STUDENT.ARV.2X(0.05;5) = 2.57058
STUDENT.TEST is a function for testing the hypothesis about the equality of mathematical expectations in two samples. Replaces a bunch of calculations, because It is enough to specify only two ranges with data and a couple more parameters. The output will be p-value.
CONFIDENCE.STUDENT – calculation of the confidence interval of the average taking into account the t-distribution.
Let's consider this training example. At the enterprise, cement is packaged in 50 kg bags. Due to randomness, some deviation from the expected mass is allowed in a single bag, but the general average should remain 50 kg. The quality control department randomly weighed 9 bags and obtained the following results: average weight ( X̅) was 50.3 kg, standard deviation ( s) – 0.5 kg.
Is this result consistent with the null hypothesis that the general mean is 50 kg? In other words, is it possible to obtain such a result by pure chance if the equipment is working properly and produces an average filling of 50 kg? If the hypothesis is not rejected, then the resulting difference fits into the range of random fluctuations, but if the hypothesis is rejected, then most likely there was a malfunction in the settings of the machine that fills the bags. It needs to be checked and configured.
A short condition in generally accepted notation looks like this.
H0: μ = 50 kg
H a: μ ≠ 50 kg
There is reason to assume that the distribution of bag fills follows a normal distribution (or does not differ much from it). This means that to test the hypothesis about the mathematical expectation, you can use the Student t-test. Random deviations can occur in any direction, which means a two-sided t-test is needed.
First, we will use antediluvian means: manually calculating the t-criterion and comparing it with the critical table value. Calculated t-test:
![]()
Now let’s determine whether the resulting number exceeds the critical level at the significance level α = 0.05. Let's use the Student's t-distribution table (available in any statistics textbook).

The columns show the probability of the right side of the distribution, and the rows show the number of degrees of freedom. We are interested in a two-tailed t-test with a significance level of 0.05, which is equivalent to the t-value for half the significance level on the right: 1 - 0.05/2 = 0.975. The number of degrees of freedom is the sample size minus 1, i.e. 9 - 1 = 8. At the intersection we find the table value of the t-test - 2.306. If we used the standard normal distribution, then the critical point would be the value of 1.96, but here it is greater, because The t-distribution in small samples has a more flattened appearance.
Let's compare the actual (1.8) and table value (2.306). The calculated criterion turned out to be less than the tabulated one. Consequently, the available data do not contradict the hypothesis H 0 that the general average is 50 kg (but do not prove it either). That's all we can learn using tables. You can, of course, also try to find the p-value, but it will be approximate. And, as a rule, it is the p-value that is used to test hypotheses. Therefore, we next move to Excel.
There is no ready-made function for calculating the t-test in Excel. But this is not scary, because the Student’s t-test formula is quite simple and can be easily built right in an Excel cell.

We got the same 1.8. Let us first find the critical value. We take alpha 0.05, the criterion is two-sided. We need the inverse t-distribution function for the two-sided hypothesis STUDENT.OBR.2X.

The resulting value cuts off the critical region. The observed t-test does not fall into it, so the hypothesis is not rejected.
However, this is the same way of testing a hypothesis using a table value. It would be more informative to calculate the p-value, i.e. the probability of obtaining the observed or even greater deviation from the average of 50 kg, if this hypothesis is correct. You will need the Student distribution function for the two-sided hypothesis STUDENT.DIST.2X.

The P-value is 0.1096, which is greater than the acceptable significance level of 0.05 – we do not reject the hypothesis. But now we can judge the degree of evidence. The P-value turned out to be quite close to the level where the hypothesis is rejected, and this leads to different thoughts. For example, that the sample was too small to detect a significant deviation.
After some time, the control department again decided to check how the bag filling standard was being maintained. This time, for greater reliability, not 9, but 25 bags were selected. It is intuitively clear that the spread of the average will decrease, and, therefore, the chances of finding a failure in the system become greater.
Let's say the same values of the mean and standard deviation for the sample were obtained as the first time (50.3 and 0.5, respectively). Let's calculate the t-test.
![]()
The critical value for 24 degrees of freedom and α = 0.05 is 2.064. The picture below shows that the t-test falls within the range of hypothesis rejection.

We can conclude that with a confidence probability of more than 95%, the general average differs from 50 kg. To be more convincing, let's look at the p-value (last row in the table). The probability of obtaining an average with the same or even greater deviation from 50, if the hypothesis is correct, is 0.0062, or 0.62%, which is practically impossible with a single measurement. In general, we reject the hypothesis as unlikely.
Calculating a Confidence Interval Using the Student's t-Distribution
Another one closely related to hypothesis testing is statistical method – calculation of confidence intervals. If the resulting interval contains a value corresponding to the null hypothesis, then this is equivalent to the fact that the null hypothesis is not rejected. Otherwise, the hypothesis is rejected with the corresponding confidence level. In some cases, analysts do not test hypotheses in the classical form at all, but only calculate confidence intervals. This approach allows you to extract even more useful information.
Let's calculate confidence intervals for the mean for 9 and 25 observations. To do this, we will use the Excel function CONFIDENT.STUDENT. Here, oddly enough, everything is quite simple. The function arguments only need to indicate the significance level α , sample standard deviation and sample size. At the output we get the half-width of the confidence interval, that is, the value that needs to be placed on both sides of the average. Having carried out the calculations and drawn a visual diagram, we get the following.

As you can see, with a sample of 9 observations, the value 50 falls within the confidence interval (the hypothesis is not rejected), and with 25 observations it does not fall within the confidence interval (the hypothesis is rejected). Moreover, in an experiment with 25 bags, it can be stated that with a probability of 97.5% the general average exceeds 50.1 kg (the lower limit of the confidence interval is 50.094 kg). And this is quite valuable information.
Thus, we solved the same problem in three ways:
1. Using an ancient approach, comparing the calculated and tabulated values of the t-test
2. More modern, by calculating the p-value, adding a degree of confidence when rejecting the hypothesis.
3. Even more informative by calculating the confidence interval and obtaining the minimum value of the general average.
It is important to remember that the t-test refers to parametric methods, because is based on a normal distribution (it has two parameters: mean and variance). Therefore, for its successful application, at least approximate normality of the initial data and the absence of outliers are important.
Finally, I suggest watching a video on how to carry out calculations related to the Student t-test in Excel.
Student's t-test – common name for a class of methods for statistical testing of hypotheses (statistical tests) based on the Student distribution. The most common uses of the t-test involve testing the equality of means in two samples.
1. History of the development of the t-test
This criterion was developed William Gossett to assess the quality of beer in the Guinness company. Due to obligations to the company regarding non-disclosure of trade secrets, Gosset's article was published in 1908 in the journal Biometrics under the pseudonym "Student".
2. What is the Student's t-test used for?
Student's t test is used to determine the statistical significance of differences in means. Can be used both in cases of comparison of independent samples ( for example, groups of diabetics and healthy groups), and when comparing related populations ( for example, average heart rate in the same patients before and after taking an antiarrhythmic drug).
3. In what cases can the Student’s t-test be used?
To apply the Student t-test, it is necessary that the original data have normal distribution. In the case of applying a two-sample criterion for independent samples, it is also necessary to satisfy the condition equality (homoscedasticity) of variances.
If these conditions are not met, similar methods should be used when comparing sample means. nonparametric statistics, among which the most famous are Mann-Whitney U test(as a two-sample test for independent samples), and sign criterion And Wilcoxon test(used in cases of dependent samples).
4. How to calculate Student's t-test?
To compare average values, Student's t-test is calculated using the following formula:
Where M 1- arithmetic mean of the first compared population (group), M 2- arithmetic mean of the second compared population (group), m 1- average error of the first arithmetic mean, m 2- average error of the second arithmetic mean.
5. How to interpret the Student's t-test value?
The resulting Student's t-test value must be interpreted correctly. To do this, we need to know the number of subjects in each group (n 1 and n 2). Finding the number of degrees of freedom f according to the following formula:
f = (n 1 + n 2) - 2After this, we determine the critical value of the Student’s t-test for the required level of significance (for example, p = 0.05) and for a given number of degrees of freedom f according to the table ( see below).
We compare the critical and calculated values of the criterion:
- If the calculated value of Student's t-test equal or greater critical, found from the table, we conclude that the differences between the compared values are statistically significant.
- If the value of the calculated Student's t-test less tabular, which means the differences between the compared values are not statistically significant.
6. Example of calculating Student's t-test
To study the effectiveness of a new iron preparation, two groups of patients with anemia were selected. In the first group, patients received a new drug for two weeks, and in the second group they received a placebo. After this, hemoglobin levels in peripheral blood were measured. In the first group average level hemoglobin was 115.4±1.2 g/l, and in the second - 103.7±2.3 g/l (data are presented in the format M±m), the populations being compared have a normal distribution. The number of the first group was 34, and the second - 40 patients. It is necessary to draw a conclusion about the statistical significance of the differences obtained and the effectiveness of the new iron preparation.
Solution: To assess the significance of differences, we use Student’s t-test, calculated as the difference in mean values divided by the sum of squared errors:

After performing the calculations, the t-test value turned out to be 4.51. We find the number of degrees of freedom as (34 + 40) - 2 = 72. We compare the resulting Student's t-test value of 4.51 with the critical value at p = 0.05 indicated in the table: 1.993. Since the calculated value of the criterion is greater than the critical value, we conclude that the observed differences are statistically significant (significance level p<0,05).
The t-test was developed by William Gosset (1876-1937) to evaluate the quality of beer at the Guinness breweries in Dublin, Ireland. In connection with obligations to the company regarding non-disclosure of trade secrets (Guinness management considered the use of statistical apparatus in its work as such), Gosset’s article was published in 1908 in the journal Biometrics under the pseudonym “Student”.
The Student's test is aimed at assessing the differences in the average values of two samples that are normally distributed. One of the main advantages of the criterion is the breadth of its application. It can be used to compare means y, and the samples may not be equal in size.
Conditions for using Student's t-test
To apply the Student t-test, the following conditions must be met:
1. The measurement can be .
2. The compared samples must be distributed according to the normal law.
Automatic calculation of Student's t-test
Step 1
To make the correct calculation using this script, you must:
1) Select the calculation for the case with disconnected (independent) or connected (dependent) samples.
2) Enter the data of the first sample in the first column (“Sample 1”), and the data of the second sample in the second column (“Sample 2”). Data is entered one number per line; no spaces, omissions, etc. Only numbers are entered. Fractional numbers are entered with a “.” (dot).
3) After filling out the columns, click on the “Step 2” button to automatically calculate the Student’s t-test.
where f is the degree of freedom, which is defined as

Example . Two groups of students were trained using two different methods. At the end of the training, they were given a test throughout the course. It is necessary to assess how significant the differences in acquired knowledge are. The test results are presented in Table 4.
Table 4
Let's calculate the sample mean, variance and standard deviation:
Let's determine the value of t p using the formula t p = 0.45
Using Table 1 (see appendix) we find the critical value t k for the significance level p = 0.01
Conclusion: since the calculated value of the criterion is less than the critical value of 0.45<2,88 гипотеза Но подтверждается и существенных различий в методиках обучения нет на уровне значимости 0,01.
Algorithm for calculating Student's t-test for dependent samples of measurements
1. Determine the calculated value of the t-test using the formula
 , Where
, Where 


3. Determine the critical value of the t-test according to Table 1 of the Appendix.
4. Compare the calculated and critical value of the t-test. If the calculated value is greater than or equal to the critical value, then the hypothesis of equality of average values in two samples of changes is rejected (Ho). In all other cases it is accepted at a given significance level.
U- criterionManna- Whitney
Purpose of the criterion
The criterion is intended to assess differences between two non-parametric samples in terms of the level of any quantitatively measured characteristic. It allows you to identify differences between small samples when n< 30.
Description of criterion
This method determines whether the area of overlapping values between two series is small enough. The smaller this area, the more likely it is that the differences are significant. The empirical value of the U criterion reflects how large the area of agreement between the rows is. Therefore, the smaller U is, the more likely it is that the differences are significant.
Hypotheses
BUT: The level of the trait in group 2 is not lower than the level of the trait in group 1.
HI: The level of the trait in group 2 is lower than the level of the trait in group 1.
Algorithm for calculating the Mann-Whitney criterion (u)
Transfer all test subjects’ data to individual cards.
Mark the cards of the subjects in sample 1 with one color, say red, and all the cards from sample 2 with another color, for example, blue.
Arrange all the cards in a single row according to the degree of increase in the attribute, regardless of which sample they belong to, as if we were working with one large sample.

where n 1 is the number of subjects in sample 1;
n 2 – number of subjects in sample 2,
T x – the larger of the two rant amounts;
n x – the number of subjects in the group with a larger sum of ranks.
9. Determine the critical values of U according to table 2 (see appendix).
If U em.> U cr0.05, then the hypothesis But is accepted. If U emp.≤ U cr, then it is rejected. The smaller the U value, the higher the reliability of the differences.
Example. Compare the effectiveness of two teaching methods in two groups. The test results are presented in Table 5.
Table 5
Let's transfer all the data to another table, highlighting the data of the second group with an underline, and make a ranking of the overall sample (see the ranking algorithm in the guidelines for task 3).
|
Values | ||||||||||||||||||
Let's find the sum of the ranks of two samples and choose the larger one: T x = 113
Let's calculate the empirical value of the criterion using formula 2: U p = 30.
Using table 2 in the appendix, we determine the critical value of the criterion at the significance level p = 0.05: U k = 19.
Conclusion: since the calculated value of the criterionUis greater than critical at the significance level p = 0.05 and 30 > 19, then the hypothesis about the equality of means is accepted and the differences in teaching methods are insignificant.