Let's start studying the topic Indefinite integral", and also analyze in detail examples of solutions to the simplest (and not quite) integrals. As usual, we will limit ourselves to the minimum theory that is in numerous textbooks, our task is to learn how to solve integrals.
What do you need to know to successfully master the material? In order to cope with integral calculus, you need to be able to find derivatives, at least at an average level. It will not be superfluous experience if you have several dozen, or better, a hundred independently found derivatives behind you. At the very least, you should not be confused by the task of differentiating the simplest and most common functions.
It would seem, where are the derivatives at all, if we are talking about integrals in the article?! And here's the thing. The fact is that finding derivatives and finding indefinite integrals (differentiation and integration) are two mutually inverse actions, such as addition / subtraction or multiplication / division. Thus, without a skill and some kind of experience in finding derivatives, unfortunately, one cannot advance further.
In this regard, we will need the following methodological materials: Derivative table and Table of integrals.
What is the difficulty of studying indefinite integrals? If in derivatives there are strictly 5 rules of differentiation, a table of derivatives and a fairly clear algorithm of actions, then in integrals everything is different. There are dozens of integration methods and techniques. And, if the integration method was initially chosen incorrectly (that is, you don’t know how to solve it), then the integral can literally be “pricked” for literally days, like a real rebus, trying to notice various tricks and tricks. Some even like it.
By the way, we quite often heard from students (not humanities) an opinion like: “I never had an interest in solving the limit or derivative, but integrals are a completely different matter, it’s exciting, there is always a desire to “crack” a complex integral” . Stop. Enough black humor, let's move on to these very indefinite integrals.
Since there are many ways to solve, then where does a teapot start studying indefinite integrals? In integral calculus, in our opinion, there are three pillars or a kind of "axis" around which everything else revolves. First of all, you should have a good understanding of the simplest integrals (this article).
Then you need to work out the lesson in detail. THIS IS THE MOST IMPORTANT RECEPTION! Perhaps even the most important article of all articles devoted to integrals. And thirdly, be sure to read integration by parts, because it integrates a wide class of functions. If you master at least these three lessons, then there are already “not two”. You can be forgiven for not knowing integrals of trigonometric functions, integrals of fractions, integrals of fractional rational functions, integrals of irrational functions (roots), but if you “get into a puddle” on the replacement method or the integration by parts method, then it will be very, very bad.
So, let's start simple. Let's look at the table of integrals. As in derivatives, we notice several integration rules and a table of integrals of some elementary functions. Any tabular integral (and indeed any indefinite integral) has the form:
Let's get straight to the notation and terms:
- integral icon.
- integrand function (written with the letter "s").
– differential icon. What it is, we will consider very soon. The main thing is that when writing the integral and during the solution, it is important not to lose this icon. There will be a noticeable flaw.
is the integrand or "stuffing" of the integral.
– antiderivative function.
– . There is no need to be heavily loaded with terms, the most important thing here is that in any indefinite integral, a constant is added to the answer.
To solve an indefinite integral means to findset of antiderivative functions from the given integrand
Let's take a look at the entry again:
Let's look at the table of integrals.
What's happening? Our left parts are turning to other functions: .
Let's simplify our definition:
Solve the indefinite integral - it means to TURN it into an indefinite (up to a constant) function , using some rules, techniques and a table.
Take, for example, the table integral 
. What happened? The symbolic record has turned into a set of antiderivative functions.
As in the case of derivatives, in order to learn how to find integrals, it is not necessary to be aware of what an integral is, or an antiderivative function from a theoretical point of view. It is enough just to carry out transformations according to some formal rules. So, in case it is not at all necessary to understand why the integral turns into exactly. You can take this and other formulas for granted. Everyone uses electricity, but few people think about how electrons run along the wires.
Since differentiation and integration are opposite operations, then for any antiderivative that is found correctly, the following is true:
In other words, if the correct answer is differentiated, then the original integrand must be obtained.
Let's go back to the same table integral .
Let's verify the validity of this formula. We take the derivative of the right side:
is the original integrand.
By the way, it became clearer why a constant is always assigned to a function. When differentiating, a constant always turns into zero.
Solve the indefinite integral it means to find lots of all antiderivatives, and not some single function. In the considered tabular example, , , , etc. - all these functions are the solution of the integral . There are infinitely many solutions, so they write briefly:
Thus, any indefinite integral is easy enough to check. This is some compensation for a large number of integrals of different types.
Let's move on to specific examples. Let's start, as in the study of the derivative, with two rules of integration:
- constant C can (and should) be taken out of the integral sign.
– the integral of the sum (difference) of two functions is equal to the sum (difference) of two integrals. This rule is valid for any number of terms.
As you can see, the rules are basically the same as for derivatives. Sometimes they are called linearity properties integral.
Example 1
Find the indefinite integral.
.
Run a check.
Solution: It is more convenient to convert it like.
(1) Applying the rule . Don't forget to write down the differential icon dx under each integral. Why under each? dxis a full multiplier. If you paint in detail, then the first step should be written as follows:
.
(2) According to the rule we take all the constants out of the signs of the integrals. Note that in the last term tg 5 is a constant, we also take it out.
In addition, at this step we prepare the roots and degrees for integration. In the same way as in differentiation, the roots must be represented in the form . Roots and degrees that are located in the denominator - move up.
Note: unlike derivatives, roots in integrals do not always need to be reduced to the form , and move the degrees up.
For example, - this is a ready-made tabular integral, which has already been calculated before you, and all sorts of Chinese tricks like 
completely unnecessary. Similarly: - this is also a tabular integral, there is no point in representing a fraction in the form . Study the table carefully!
(3) All integrals are tabular. We carry out the transformation using the table, using the formulas: 
, and
for a power function - 
.
It should be noted that the table integral is a special case of the formula for a power function: 
.
Constant C just add it once at the end of the expression
(rather than putting them after each integral).
(4) We write the result obtained in a more compact form, when all degrees of the form
again represent as roots, and the powers with a negative exponent are reset back to the denominator.
Examination. In order to perform the check, you need to differentiate the received answer:
Initial integrand, i.e., the integral was found correctly. From what they danced, to that they returned. It's good when the story with the integral ends just like that.
From time to time, there is a slightly different approach to checking the indefinite integral, when not the derivative, but the differential is taken from the answer:
.
As a result, we obtain not an integrand, but an integrand.
Do not be afraid of the concept of differential.
The differential is the derivative multiplied by dx.
However, it is not theoretical subtleties that are important to us, but what to do next with this differential. The differential is revealed as follows: icon d remove, put a stroke on the right above the bracket, assign a multiplier at the end of the expression dx :
Received original integrand, that is, the integral is found correctly.
As you can see, the differential comes down to finding the derivative. I like the second way of checking less, since I have to additionally draw large brackets and drag the differential icon dx until the end of the test. Although it is more correct, or "more solid", or something.
In fact, it was possible to keep silent about the second method of verification. The point is not in the method, but in the fact that we have learned to open the differential. Again.
The differential is revealed as follows:
1) icon d remove;
2) put a stroke on the right above the bracket (the designation of the derivative);
3) at the end of the expression we assign a factor dx .
For example:
Remember this. We will need the considered technique very soon.
Example 2
.
When we find an indefinite integral, we ALWAYS try to check Moreover, there is a great opportunity for this. Not all types of problems in higher mathematics are a gift from this point of view. It does not matter that verification is often not required in control tasks, no one, and nothing prevents it from being carried out on a draft. An exception can be made only when there is not enough time (for example, at the test, exam). Personally, I always check integrals, and I consider the lack of verification to be a hack and a poorly completed task.
Example 3
Find the indefinite integral:
. Run a check.
Solution: Analyzing the integral, we see that under the integral we have the product of two functions, and even the exponentiation of the whole expression. Unfortunately, in the field of integral battle No good and comfortable formulas for integrating the product and the quotient as: 
or 
.
Therefore, when a product or a quotient is given, it always makes sense to see if it is possible to transform the integrand into a sum? The considered example is the case when it is possible.
First, we give the complete solution, the comments will be below.
Initial integrand, which means that the integral is found correctly.
In the course of checking, it is always desirable to “pack” the function to its original form, taking, in this case, out of the brackets and applying the abbreviated multiplication formula in the opposite direction: .
Example 4
Find the indefinite integral
Run a check.
This is an example for self-solving. Answer and complete solution at the end of the lesson.
Example 5
Find the indefinite integral
. Run a check.
In this example, the integrand is a fraction. When we see a fraction in the integrand, the first thought should be the question: “Is it possible to somehow get rid of this fraction, or at least simplify it?”.
We notice that the denominator contains a lone root of "x". One in the field is not a warrior, which means that you can divide the numerator into the denominator term by term:
We do not comment on actions with fractional powers, since they have been repeatedly discussed in articles on the derivative of a function.
If you are still confused by such an example as
and no one gets the right answer,
Also note that the solution skips one step, namely applying the rules , . Usually, with a certain experience in solving integrals, these rules are considered an obvious fact and are not described in detail.
Example 6
Find the indefinite integral. Run a check.
This is an example for self-solving. Answer and complete solution at the end of the lesson.
In the general case, with fractions in integrals, everything is not so simple, additional material on the integration of fractions of some types can be found in the article: Integration of some fractions. But, before moving on to the above article, you need to read the lesson: Replacement method in indefinite integral. The fact is that summing a function under a differential or a variable change method is key point in the study of the topic, since it is found not only "in pure assignments for the replacement method", but also in many other varieties of integrals.
Solutions and answers:
Example 2: Solution:
Example 4: Solution:
In this example, we used the reduced multiplication formula
Example 6: Solution:
Integrals online to the site to consolidate the material covered by students and schoolchildren. Every time, as soon as you start solving the integral, you need to identify its type, without this you can not use any method, except for its tabular. Not every table integral is clearly visible from a given example, sometimes you need to transform the original function in order to find the antiderivative. In practice, the solution of integrals comes down to interpreting the problem of finding the original, that is, the antiderivative from an infinite family of functions, but if the limits of integration are given, then according to the Newton-Leibniz formula, there remains only one single function to which calculations will need to be applied. Informally, the online integral is the area between the graph of the function and the x-axis within the integration. Let us calculate the complex integral over one variable and relate its answer to the further solution of the problem. You can, as they say, directly find it from the integrand. According to the fundamental theorem of analysis, integration is the inverse operation of differentiation, which helps to solve differential equations. There are several different definitions of the operation of integration, differing in technical details. However, they are all compatible, that is, any two integration methods, if they can be applied to a given function, will give the same result. The simplest is the Riemann integral - it is a definite integral or an indefinite integral. Informally, the integral of one variable can be entered as the area under the graph (the figure enclosed between the graph of the function and the x-axis). Trying to find this area, one can consider figures consisting of a number of vertical rectangles, the bases of which together form an integration segment and are obtained by dividing the segment into the corresponding number of small segments. The calculator solves integrals with a description of the actions in detail and for free! The online indefinite integral for a function is the totality of all antiderivatives of the given function. If a function is defined and continuous on an interval, then it has an antiderivative function (or a family of antiderivatives). It is better to carefully approach this matter and experience inner satisfaction from the work done. But to calculate the integral in a way different from the classical one, sometimes leads to unexpected results and one should not be surprised at this. Pleased with the fact that will have a positive impact on what is happening. List of definite integrals and indefinite integrals with full detailed step by step solution. Finding the indefinite integral online is a very common task in higher mathematics and other technical branches of science. Basic methods of integration. Think about completed buildings before mistakes are found. Solving integrals online - you will get a detailed solution for different types of integrals: indefinite, definite, improper. The integral of a function is analogous to the sum of a sequence. Informally speaking, a definite integral is the area of a part of the graph of a function. Often, such an integral determines how much heavier a body is compared to an object of the same density, and it does not matter what shape it is, because the surface does not absorb water. Every undergraduate student knows how to find the integral online. On the basis of the school curriculum, this section of mathematics is also studied, but not in detail, but only the basics of such a complex and important topic. In most cases, students start studying integrals with an extensive theory, which is also preceded by important topics, such as the derivative and passages to the limit - they are also limits. The solution of integrals gradually begins with the most elementary examples from simple functions, and ends with the use of many approaches and rules proposed in the last century and even much earlier. Integral calculus is of an exploratory nature in lyceums and schools, that is, in secondary educational institutions. Our site site will always help you and solving integrals online will become an ordinary, and most importantly, understandable task for you. Based on this resource, you can easily achieve excellence in this mathematical section. Comprehending step by step the studied rules, for example, such as integration, by parts or the application of the Chebyshev method, you can easily solve any test for the maximum number of points. So how can we still calculate the integral using the table of integrals known to everyone, but in such a way that the solution is correct, correct and with the most accurate answer possible? How to learn this and is it possible for an ordinary freshman to do it in the shortest possible time? We answer this question in the affirmative - it is possible! In this case, you will not only be able to solve any example, but also reach the level of a high-class engineer. The secret is as simple as ever - you need to make the maximum effort, devote the necessary amount of time to self-preparation. Unfortunately, no one has yet come up with a different way! But not everything is as cloudy as it seems at first glance. If you refer to our site service with this question, then we will make your life easier, because our site can calculate integrals online in detail, at a very high speed and with an impeccably accurate answer. At its core, the integral does not determine how the ratio of arguments affects the stability of the system as a whole. The mechanical meaning of the integral lies in many applied problems, this is the determination of the volume of bodies, and the calculation of body mass. Triple and double integrals are involved in just these calculations. We insist that online integrals be solved only under the supervision of experienced teachers and through numerous checks. We are often asked about the progress of students who do not attend lectures, skip them for no reason, how do they manage to find the integral themselves. We answer that students are free people and may well be trained externally, preparing for a test or exam in comfortable home conditions. In a matter of seconds, our service will help anyone who wants to calculate the integral of any given function with respect to a variable. Check the result obtained by taking the derivative of the antiderivative function. In this case, the constant from the solution of the integral vanishes. This rule is obviously for everyone. There are not many such sites that give a step-by-step answer in a matter of seconds, and most importantly with high accuracy and in a convenient form. But we should not forget about how it is possible to find the integral using a ready-made service, time-tested and tested on thousands of solved examples online.
Complex integrals
This article completes the topic of indefinite integrals, and it includes integrals that I consider quite difficult. The lesson was created at the repeated request of visitors who expressed their wish that more difficult examples be analyzed on the site.
It is assumed that the reader of this text is well prepared and knows how to apply the basic techniques of integration. Dummies and people who are not very confident in integrals should refer to the very first lesson - Indefinite integral. Solution examples where you can learn the topic almost from scratch. More experienced students can get acquainted with the techniques and methods of integration, which have not yet been encountered in my articles.
What integrals will be considered?
First, we consider integrals with roots, for the solution of which we successively use variable substitution and integration by parts. That is, in one example, two methods are combined at once. And even more.
Then we will get acquainted with an interesting and original method of reducing the integral to itself. Not so few integrals are solved in this way.
The third number of the program will be integrals of complex fractions, which flew past the cash register in previous articles.
Fourthly, additional integrals from trigonometric functions will be analyzed. In particular, there are methods that avoid the time-consuming universal trigonometric substitution.
(2) In the integrand, we divide the numerator by the denominator term by term.
(3) We use the property of linearity of the indefinite integral. In the last integral, immediately bring the function under the sign of the differential.
(4) We take the remaining integrals. Note that you can use brackets in the logarithm and not the modulus, because .
(5) We carry out the reverse substitution, expressing from the direct substitution "te":
Masochistic students can differentiate the answer and get the original integrand, as I just did. No, no, I did the check in the right sense =)
As you can see, in the course of the solution, even more than two solution methods had to be used, so to deal with such integrals, you need confident integration skills and not the least experience.
In practice, of course, the square root is more common, here are three examples for an independent solution:
Example 2
Find the indefinite integral
Example 3
Find the indefinite integral
Example 4
Find the indefinite integral
These examples are of the same type, so the complete solution at the end of the article will be only for Example 2, in Examples 3-4 - one answer. Which replacement to use at the beginning of decisions, I think, is obvious. Why did I choose the same type of examples? Often found in their roles. More often, perhaps, just something like 
.
But not always, when the root of a linear function is under the arc tangent, sine, cosine, exponent, and other functions, several methods have to be applied at once. In a number of cases, it is possible to “get off easy”, that is, immediately after the replacement, a simple integral is obtained, which is taken elementarily. The easiest of the tasks proposed above is Example 4, in which, after the replacement, a relatively simple integral is obtained.
The method of reducing the integral to itself
Clever and beautiful method. Let's take a look at the classics of the genre:
Example 5
Find the indefinite integral
There is a square binomial under the root, and when trying to integrate this example, the teapot can suffer for hours. Such an integral is taken by parts and reduces to itself. In principle, it is not difficult. If you know how.
Let us denote the considered integral by a Latin letter and start the solution: 
Integrating by parts: 
(1) We prepare the integrand for term-by-term division.
(2) We divide the integrand term by term. Perhaps not everyone understands, I will write in more detail:
(3) We use the property of linearity of the indefinite integral.
(4) We take the last integral ("long" logarithm).
Now let's look at the very beginning of the solution: 
And for the ending: 
What happened? As a result of our manipulations, the integral has reduced to itself!
Equate the beginning and end: 
We transfer to the left side with a change of sign: 
And we demolish the deuce to the right side. As a result: 
The constant, strictly speaking, should have been added earlier, but I added it at the end. I strongly recommend reading what is the severity here:
Note:
More strictly, the final stage of the solution looks like this:
In this way:
The constant can be re-named with . Why can you rename? Because it still takes any values, and in this sense there is no difference between constants and.
As a result:
A similar trick with constant renaming is widely used in differential equations. And there I will be strict. And here such liberties are allowed by me only in order not to confuse you with unnecessary things and focus on the integration method itself.
Example 6
Find the indefinite integral
Another typical integral for independent solution. Full solution and answer at the end of the lesson. The difference with the answer of the previous example will be!
If there is a square trinomial under the square root, then the solution in any case reduces to the two analyzed examples.
For example, consider the integral 
. All you need to do is in advance select a full square:
.
Next, a linear replacement is carried out, which manages "without any consequences":
, resulting in an integral . Something familiar, right?
Or this example, with a square binomial:
Selecting a full square:
And, after a linear replacement , we get the integral , which is also solved by the already considered algorithm.
Consider two more typical examples of how to reduce an integral to itself:
is the integral of the exponent multiplied by the sine;
is the integral of the exponent multiplied by the cosine.
In the listed integrals by parts, you will have to integrate twice already:
Example 7
Find the indefinite integral
The integrand is the exponent multiplied by the sine.
We integrate by parts twice and reduce the integral to itself: 
As a result of double integration by parts, the integral is reduced to itself. Equate the beginning and end of the solution:
We transfer to the left side with a change of sign and express our integral: 
Ready. Along the way, it is desirable to comb the right side, i.e. take the exponent out of brackets, and place the sine and cosine in brackets in a “beautiful” order.
Now let's go back to the beginning of the example, or rather, to integration by parts: 
For we have designated the exhibitor. The question arises, it is the exponent that should always be denoted by ? Not necessary. In fact, in the considered integral fundamentally doesn't matter, what to denote for, one could go the other way: 
Why is this possible? Because the exponent turns into itself (when differentiating and integrating), the sine and cosine mutually turn into each other (again, both when differentiating and integrating).
That is, the trigonometric function can be denoted as well. But, in the considered example, this is less rational, since fractions will appear. If you wish, you can try to solve this example in the second way, the answers must be the same.
Example 8
Find the indefinite integral
This is a do-it-yourself example. Before deciding, think about what is more profitable in this case to designate for, exponential or trigonometric function? Full solution and answer at the end of the lesson.
And, of course, don't forget that most of the answers in this lesson are fairly easy to check by differentiation!
The examples were considered not the most difficult. In practice, integrals are more common, where the constant is both in the exponent and in the argument of the trigonometric function, for example: . Many people will have to get confused in such an integral, and I myself often get confused. The fact is that in the solution there is a high probability of the appearance of fractions, and it is very easy to lose something due to inattention. In addition, there is a high probability of error in signs, note that there is a minus sign in the exponent, and this introduces additional difficulty.
At the final stage, it often turns out something like this:
Even at the end of the solution, you should be extremely careful and correctly deal with fractions: 
Integration of complex fractions
We are slowly approaching the equator of the lesson and begin to consider integrals of fractions. Again, not all of them are super complex, just for one reason or another, the examples were a little “off topic” in other articles.
Continuing the theme of roots
Example 9
Find the indefinite integral
In the denominator under the root there is a square trinomial plus outside the root "appendage" in the form of "X". An integral of this form is solved using a standard substitution.
We decide: 
The replacement here is simple: 
Looking at life after replacement: 
(1) After substitution, we reduce the terms under the root to a common denominator.
(2) We take it out from under the root.
(3) We reduce the numerator and denominator by . At the same time, under the root, I rearranged the terms in a convenient order. With some experience, steps (1), (2) can be skipped by performing the commented actions orally.
(4) The resulting integral, as you remember from the lesson Integration of some fractions, is solved full square selection method. Select a full square.
(5) By integration, we obtain an ordinary "long" logarithm.
(6) We carry out the reverse replacement. If initially , then back: .
(7) The final action is aimed at hairdressing the result: under the root, we again bring the terms to a common denominator and take them out from under the root.
Example 10
Find the indefinite integral 
This is a do-it-yourself example. Here, a constant is added to the lone x, and the replacement is almost the same: 
The only thing that needs to be done additionally is to express the "x" from the replacement: 
Full solution and answer at the end of the lesson.
Sometimes in such an integral there may be a square binomial under the root, this does not change the way the solution is solved, it will even be even simpler. Feel the difference:
Example 11
Find the indefinite integral
Example 12
Find the indefinite integral
Brief solutions and answers at the end of the lesson. It should be noted that Example 11 is exactly binomial integral, the solution method of which was considered in the lesson Integrals of irrational functions.
Integral of an indecomposable polynomial of the 2nd degree to the degree
(polynomial in denominator)
A rarer, but, nevertheless, occurring in practical examples form of the integral.
Example 13
Find the indefinite integral
But let's go back to the example with the lucky number 13 (honestly, I didn't guess). This integral is also from the category of those with which you can pretty much suffer if you don’t know how to solve.
The solution starts with an artificial transformation: 
I think everyone already understands how to divide the numerator by the denominator term by term.
The resulting integral is taken in parts: 
For an integral of the form ( is a natural number), we have derived recurrent downgrading formula:
, where 
is an integral of a lower degree.
Let us verify the validity of this formula for the solved integral .
In this case: , , we use the formula: 
As you can see, the answers are the same.
Example 14
Find the indefinite integral
This is a do-it-yourself example. The sample solution uses the above formula twice in succession.
If under the degree is indecomposable square trinomial, then the solution is reduced to a binomial by extracting the full square, for example:
What if there is an additional polynomial in the numerator? In this case, the method of indeterminate coefficients is used, and the integrand is expanded into a sum of fractions. But in my practice of such an example never met, so I skipped this case in the article Integrals of a fractional-rational function, I'll skip it now. If such an integral still occurs, see the textbook - everything is simple there. I do not consider it expedient to include material (even simple), the probability of meeting with which tends to zero.
Integration of complex trigonometric functions
The adjective "difficult" for most examples is again largely conditional. Let's start with tangents and cotangents in high powers. From the point of view of the methods used to solve the tangent and cotangent are almost the same, so I will talk more about the tangent, meaning that the demonstrated method of solving the integral is valid for the cotangent too.
In the above lesson, we looked at universal trigonometric substitution for solving a certain type of integrals of trigonometric functions. The disadvantage of the universal trigonometric substitution is that its application often leads to cumbersome integrals with difficult calculations. And in some cases, the universal trigonometric substitution can be avoided!
Consider another canonical example, the integral of unity divided by the sine:
Example 17
Find the indefinite integral
Here you can use the universal trigonometric substitution and get the answer, but there is a more rational way. I will provide a complete solution with comments for each step:
(1) We use the trigonometric formula for the sine of a double angle.
(2) We carry out an artificial transformation: In the denominator we divide and multiply by .
(3) According to the well-known formula in the denominator, we turn the fraction into a tangent.
(4) We bring the function under the sign of the differential.
(5) We take the integral.
A couple of simple examples to solve on your own:
Example 18
Find the indefinite integral
Hint: The very first step is to use the reduction formula 
and carefully carry out actions similar to the previous example.
Example 19
Find the indefinite integral
Well, this is a very simple example.
Complete solutions and answers at the end of the lesson.
I think now no one will have problems with integrals: 
etc.
What is the idea behind the method? The idea is to use transformations, trigonometric formulas to organize only tangents and the derivative of the tangent in the integrand. That is, we are talking about replacing: 
. In Examples 17-19, we actually used this replacement, but the integrals were so simple that it was done with an equivalent action - bringing the function under the differential sign.
Similar reasoning, as I have already mentioned, can be carried out for the cotangent.
There is also a formal prerequisite for applying the above substitution:
The sum of the powers of cosine and sine is a negative integer EVEN number, for example:
for an integral, an integer negative EVEN number.
! Note : if the integrand contains ONLY a sine or ONLY a cosine, then the integral is taken even with a negative odd degree (the simplest cases are in Examples No. 17, 18).
Consider a couple of more meaningful tasks for this rule:
Example 20
Find the indefinite integral
The sum of the degrees of sine and cosine: 2 - 6 \u003d -4 - a negative integer EVEN number, which means that the integral can be reduced to tangents and its derivative: 
(1) Let's transform the denominator.
(2) According to the well-known formula, we obtain .
(3) Let's transform the denominator.
(4) We use the formula 
.
(5) We bring the function under the differential sign.
(6) We carry out the replacement. More experienced students may not carry out the replacement, but still it is better to replace the tangent with one letter - there is less risk of confusion.
Example 21
Find the indefinite integral
This is a do-it-yourself example.
Hold on, the championship rounds begin =)
Often in the integrand there is a "hodgepodge":
Example 22
Find the indefinite integral 
This integral initially contains a tangent, which immediately suggests an already familiar thought:
I will leave the artificial transformation at the very beginning and the rest of the steps without comment, since everything has already been said above.
A couple of creative examples for an independent solution:
Example 23
Find the indefinite integral 
Example 24
Find the indefinite integral 
Yes, in them, of course, you can lower the degrees of the sine, cosine, use the universal trigonometric substitution, but the solution will be much more efficient and shorter if it is drawn through tangents. Full solution and answers at the end of the lesson
definite integral from a continuous function f(x) on the finite interval [ a, b] (where ) is the increment of some of its antiderivatives on this segment. (In general, understanding will be noticeably easier if you repeat the topic of the indefinite integral) In this case, the notation
As can be seen in the graphs below (the increment of the antiderivative function is indicated by ), The definite integral can be either positive or negative.(It is calculated as the difference between the value of the antiderivative in the upper limit and its value in the lower limit, i.e. as F(b) - F(a)).
Numbers a and b are called the lower and upper limits of integration, respectively, and the interval [ a, b] is the segment of integration.
Thus, if F(x) is some antiderivative function for f(x), then, according to the definition,
(38)
Equality (38) is called Newton-Leibniz formula . Difference F(b) – F(a) is briefly written like this:
Therefore, the Newton-Leibniz formula will be written as follows:
(39)
Let us prove that the definite integral does not depend on which antiderivative of the integrand is taken when calculating it. Let F(x) and F( X) are arbitrary antiderivatives of the integrand. Since these are antiderivatives of the same function, they differ by a constant term: Ф( X) = F(x) + C. That's why
Thus, it is established that on the segment [ a, b] increments of all antiderivatives of the function f(x) match.
Thus, to calculate the definite integral, it is necessary to find any antiderivative of the integrand, i.e. First you need to find the indefinite integral. Constant FROM excluded from subsequent calculations. Then the Newton-Leibniz formula is applied: the value of the upper limit is substituted into the antiderivative function b , further - the value of the lower limit a and calculate the difference F(b) - F(a) . The resulting number will be a definite integral..
At a = b accepted by definition
Example 1
Solution. Let's find the indefinite integral first:
Applying the Newton-Leibniz formula to the antiderivative
(at FROM= 0), we get
However, when calculating a definite integral, it is better not to find the antiderivative separately, but immediately write the integral in the form (39).
Example 2 Calculate a definite integral
Solution. Using the formula
Properties of the Definite Integral
Theorem 2.The value of the definite integral does not depend on the designation of the integration variable, i.e.
(40)
Let F(x) is antiderivative for f(x). For f(t) the antiderivative is the same function F(t), in which the independent variable is denoted differently. Consequently,
Based on formula (39), the last equality means the equality of the integrals
Theorem 3.The constant factor can be taken out of the sign of a definite integral, i.e.
(41)
Theorem 4.The definite integral of the algebraic sum of a finite number of functions is equal to the algebraic sum of the definite integrals of these functions, i.e.
(42)
Theorem 5.If the integration segment is divided into parts, then the definite integral over the entire segment is equal to the sum of the definite integrals over its parts, i.e. if
(43)
Theorem 6.When rearranging the limits of integration, the absolute value of the definite integral does not change, but only its sign changes, i.e.
(44)
Theorem 7(mean value theorem). The definite integral is equal to the product of the length of the integration segment and the value of the integrand at some point inside it, i.e.
(45)
Theorem 8.If the upper integration limit is greater than the lower one and the integrand is non-negative (positive), then the definite integral is also non-negative (positive), i.e. if
Theorem 9.If the upper limit of integration is greater than the lower limit and the functions and are continuous, then the inequality
can be integrated term by term, i.e.
(46)
The properties of the definite integral allow us to simplify the direct calculation of integrals.
Example 5 Calculate a definite integral
Using Theorems 4 and 3, and when finding antiderivatives - tabular integrals (7) and (6), we obtain
Definite integral with variable upper limit
Let f(x) is continuous on the interval [ a, b] function, and F(x) is its prototype. Consider the definite integral
(47)
and through t the integration variable is denoted so as not to confuse it with the upper bound. When it changes X the definite integral (47) also changes, i.e., it is a function of the upper limit of integration X, which we denote by F(X), i.e.
(48)
Let us prove that the function F(X) is antiderivative for f(x) = f(t). Indeed, differentiating F(X), we get
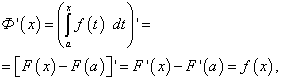
because F(x) is antiderivative for f(x), a F(a) is a constant value.
Function F(X) is one of the infinite set of antiderivatives for f(x), namely the one that x = a goes to zero. This statement is obtained if in equality (48) we put x = a and use Theorem 1 of the previous section.
Calculation of definite integrals by the method of integration by parts and the method of change of variable
where, by definition, F(x) is antiderivative for f(x). If in the integrand we make the change of variable
then, in accordance with formula (16), we can write
In this expression
antiderivative function for
Indeed, its derivative, according to the rule of differentiation of a complex function, is equal to
Let α and β be the values of the variable t, for which the function
takes respectively the values a and b, i.e.
But, according to the Newton-Leibniz formula, the difference F(b) – F(a) there is
If textbook definitions are too complicated and incomprehensible, read our article. We will try to explain as simply as possible, “on the fingers”, the main points of such a section of mathematics as definite integrals. How to calculate the integral, read in this manual.
From a geometric point of view, the integral of a function is the area of \u200b\u200bthe figure formed by the graph of this function and the axis within the integration. Write down the integral, analyze the function under the integral: if the integrand can be simplified (reduce, factor out the integral sign, split into two simple integrals), do it. Open the integral table to determine which function's derivative is under the integral. Answer found? Write down the factor taken out of the integral (if it took place), write down the function found from the table, substitute the boundaries of the integral.
Of course, only the simplest versions of integrals are considered here - certain, in fact, there are a great many varieties of integrals, they are studied in the course of higher mathematics, mathematical analysis and differential equations in universities for students of technical specialties.
