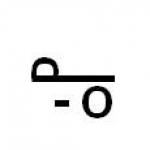LESSON SCRIPT
using a computer.
Educational institution - Municipal educational institution "Severskaya Gymnasium" ZATO Seversk.
Item - mathematics.
Class - third.
Subject: Solving equations in several steps.
Lesson type- discovery of new knowledge.
Lesson form – combined lesson with elements of problem-search learning.
Forms of organization educational activities: collective activity to solve a problem, individual tasks of choice, work in pairs, independent work.
Lesson objectives:
Educational and methodological support – textbook for third grade in 3 parts “Mathematics”, part 2, L.G. Peterson.
Lesson duration- 45 minutes.
13 slides (Power Point, Word).
Necessary equipment and materials for the lesson:
Computer, media projector, screen.
Blackboard, textbook, workbooks, media product.
Methods:
Problem
Comparative
Observation
Using schematization ( drawing up an algorithm)
Forms of work:
Collective activities
Work on options, mutual verification
Performing an optional task
Equation, components of actions, order of actions, algorithm.
Bibliography:
Textbook for third grade “Mathematics” by L.G. Peterson in 3 parts, part two, M.: Yuventa Publishing House, 2008.
L.G. Peterson “The activity approach and its implementation in mathematics lessons in elementary school,” article in the magazine “ Primary School: plus or minus", No. 5 1999
Internet resources: http:// www. cwer. ru/ files ( Pictures)
During the classes:
Lesson objectives: systematize knowledge about equations different types;
To develop the skill of finding an unknown component, to train students in commenting on equations through action components;
Introduce the algorithm for solving compound equations;
Develop computational skills, practice solving problems of the types studied;
Develop correct mathematical speech, logical thinking;
Teach self-assessment of your activities, compare the results of your activities with a model.
Organizing time(Slide No. 1).
Oral exercises (Slide No. 2).
Consider the expressions. Determine the order of actions, highlight the last action.
k m + n: 3 (5 + b): 16
a · 4 – 8 (15: x) · (8 – y)
Read the expressions based on the last action.
Introduction of new material.
(Slide No. 3)
Read the entries. Remember what each entry is called?
26 + 37 (D: expression)
236 – 21 = 215 (D: true equality)
48: x (D: variable expression)
At what values A inequality will be true?
What mathematical concept have we not named? (D: equation)
I suggest you solve several equations, but first we will repeat the rules for finding an unknown component:
Cards:
(Students repeat the rules for finding an unknown component using the cards).
Now write down the number in your notebooks and solve the following equations:
(Slide No. 4)
a – 86 = 9 56: c = 2 4 (4 b – 16) : 2 = 10
Who did the job?
How many equations did you solve? (D: two equations).
Let's check the solved equations. (Slide No. 4a).
What is the root of the first equation? (D: a = 95).
What is the root of the second equation? (D: c = 7).
What problem arose in solving the third equation?
(D: There is nothing to simplify on the right side).
Maybe someone can formulate the topic of the lesson?
(D: Solving equations in several steps).
Yes, that's right, today we will learn how to solve equations in several steps. (Slide No. 5)
Let's take a closer look at our equation again. Think about what you and I know well? What can we already do?
Children's answers (Slide No. 6):
We know how to determine the order of actions.
We know how to solve simple equations, find unknown components.
We know how to perform operations (direct and inverse).
Let's do what we know how to do, it should help us. And I will record our actions. (The teacher directs the activities of the students with an introductory dialogue; they pronounce the actions and solve the equation in their notebooks). Slide number 7
(4 ·b – 16) : 2 = 10 1. Determine the order of actions.
2. Select the last action.
3. Determine the unknown component.
4 · b – 16 = 10 · 2 4. Apply the rule.
4 ·b – 16 = 20 5. Simplify the right side.
6. We arrange the order of actions.
7. Select the last action.
8. Determine the unknown component.
4 · b = 20 + 16 9. Apply the rule.
4 · b = 36 10. Simplify the right side.
11. Determine the unknown component.
b = 36: 4 12. Apply the rule.
b = 9 13. Find the root.
Look carefully, what program of action have we come up with?
What interesting things did you notice?
Is it possible to shorten our program somehow?
Let's create an algorithm of actions:
(Slide No. 8)
Physical education minute (Slide No. 9).
Gymnastics for the eyes.
Primary consolidation (pronunciation).
(Slide number 10).
Now, using the algorithm, let's try to explain the following equation:
(2 + x: 7) · 8 = 72
2 + x: 7 = 72: 8
2 + X : 7 = 9 Students comment step by step
x: 7 = 9 – 2 solution to the equation.
Raise your hand, who clearly understands how to solve the equation in several steps? Tell us about your actions.
Who else is experiencing difficulties and needs help?
Self-control.
Check your solution, exchange notebooks, help your neighbor check.
Whoever thinks that the solution is correct, that he coped with the work, put “+” in the margin.
Check students' work. Who got the same root of the equation?
The result of the work.
Guys, what is the topic of today's lesson?
What problem did you encounter at the beginning of the lesson?
How did you cope with difficulties?
Repeat the algorithm of actions.
Do you think, while doing work now, is it only equations that we learn to solve? (D: we learn to plan our activities, practice counting, calculations, learn to complete tasks).
Can our knowledge and skills be useful in life? Where? When?
Whatever keywords highlighted in class?
(D: Equation, procedure, unknown component, rule for finding the unknown component, expressions) – Slide number 11.
8. Self-assessment of your activities.
If it was easy in the lesson, you figured it all out – the color green. If there were difficulties, doubts - yellow. If you didn’t understand the topic, it was difficult - the color red. – Slide “12.
9. Homework(Slide No. 13)
Compose your example equation in several steps;
p. 36, No. 7 (according to options).
Slide number 14 – end of the lesson.
Koryakova Lyudmila Nikolaevna, primary school teacher
Math lesson
in 4th grade
Subject:Solving equations of a new type.
Target:To promote the development of the ability to solve complex equations where the unknown is expressed by the sum or difference of numbers.
Tasks:
· develop the ability to solve complex equations where the unknown is expressed by the sum or difference of numbers;
· develop logical thinking and analytical skills;
· apply elements of health-saving technologies in the classroom;
· foster collectivism and mutual assistance.
Lesson type:Assimilation of new knowledge.
Equipment:Equation Cards; card with geometric material; board; textbook.
During the classes:
I. Organizing time:
1. Greeting guests.
2. Exercise to develop attention and memory: I will show you a card and hold it for 5 seconds. Name in order what items you remember. How many are there? (on the card there is a triangle, square, circle, rectangle, oval)
3. I wish to receive such an assessment for each of you in class.
And to do this, you need to guess these anagrams and you will find out what we will do today in class.
Anagrams: ESHARTTOAGYDAVTMSETAK
(decide) (guess) (guess)
II. Updating knowledge. Verbal counting.
1. - Name the components of addition. How to find an unknown term?
What are the components of subtraction called?
How to find the minuend? Subtrahend?
2. Expressions are given, think about where to start solving expressions where there is more than one action (from the order of actions):
Task: put actions in expressions
a + b – (d + k) : m – n
34125
500 – (280 + 120) = 100
(600 – 327) + 27 = 300
3. Solve problems:
A) Add 700 to an unknown number and get the sum 1800
1. Write an equation.
X + 700 = 1800
X = 1100
B) Subtract 60 from the unknown number and get the difference 150
1. Write an equation.
2. What is the unknown number?
X – 60 = 150
X = 210
III. Solving equations.
We have repeated the solution of simple equations, now we move on to solving more complex ones.
At the blackboard:
120 + X = 200 – 75
120 + X = 125
X = 125 – 120
X = 5
120 + 5 = 200 – 75
125 = 125
IV. Physical exercise "Gemini"
Children stand between desks, put their hands on each other's shoulders and close their eyes. On my signal they execute the following commands:
· sit down
· stand up
· stand on your toes, get down
· lean left
· lean right
· bend over backwards
· stand on your right leg with your left leg bent at the knee
· stand on your left leg with your right leg bent at the knee
· open your eyes and sit quietly
Error task:
(x + 29) – 48 = 90
Dialogue:
· What's happened?
· What did you see that was new to you?
· What was the problem?
· Let's try to solve it?
Drawing up a plan for solving the equation:
1. Let's arrange the order of actions. If this was an example, where would you start solving it?
(x + 29) – 48 = 90
2. Let's set the names of the components based on the last action. Where is the unknown number?
(x + 29) – 48 = 90
3. Express what the unknown component is equal to?
X + 29 = 90 + 48 – can we solve such an equation?
X + 29 = 138 – we got a simple equation.
X = 138 – 29
X = 109
(109 + 29) – 48 = 90
90 = 90
4. So what are we going to do in class today? (Solve equations of a new type, where the unknown is expressed as a sum or difference)
V. Can you name the topic of our lesson again? (Solving equations of a new type)
Let us repeat the algorithm for solving the equations:
1. Arrangement of the order of actions.
2. Determining the names of components based on the last action.
3. Find the minuend, subtrahend, and addend.
4. Check (procedure of action).
VI. Target:Yes, today we will learn how to solve these equations, where the unknown will be expressed as a sum or difference.
VII. Consolidating new material (at the board)
|
140 – (a + 25) = 40 a + 25 = 140 – 40 a + 25 = 100 a = 100 – 25 a = 75 _________________ 140 – (75 + 25) = 40 40 = 40 |
340 + (190 – x) = 400 190 – x = 400 – 340 190 – x = 60 x = 190 – 60 x = 130 _______________ 340 + (190 – 130) = 400 |
Physical exercise "Clowns"
Children stand freely between desks; according to my command:
· bring your eyebrows together and apart;
· squint your eyes, then open them wide;
· open your lips as much as possible in an impromptu smile, and then purse them;
· stretch your neck, then lower it;
· hug yourself with your arms, stroke them and wish you success in your studies.
VIII. Work in shift pairs.
(Give each child cards with an equation of the form: 100 – (x + 25) = 52)
What is the most important thing when working in pairs? (Help your friend)
IX. Explain how you solved the equation? (Orally)
Exercise for the eyes:
· move your eyes around the blue circle clockwise;
· red – counterclockwise; (Repeat 2-3 times)
X. Independent work (Multi-level tasks)
1 level to “3”:
189 – (x – 80) = 39
x – 80 = 189 – 39
Level 2 to “4”:
350 – (45 + a) = 60
Level 3 at “5”:
Make up an equation for the problem and solve it: From the number 280, subtract the sum of the numbers x and 40 equals 80
280 – (x + 40) = 80
x + 40 = 280 – 80
x + 40 = 200
x = 200 – 40
x = 160
________________
280 – (160 + 40) = 80
80 = 80
XI. Checking multi-level tasks (according to the example):
Level 1:
189 – (x – 80) = 39
x – 80 = 189 – 39
x – 80 = 150
x = 150 +80
x = 230
_________________
189 – (230 – 80) = 39
39 = 39
Level 2:
350 – (45 + a) = 60
45 + a = 350 – 60
45 +a = 290
a = 290 – 45
a = 245
__________________
350 – (45 + 245) = 60
60 = 60
Level 3:
280 – (x + 40) = 80
x + 40 = 280 – 80
x + 40 = 200
x = 200 – 40
x = 160
________________
280 – (160 + 40) = 80
80 = 80
XII. I evaluate children.
XIII. Lesson reflection.
How did you feel in class today?
Comfortable
Alarming
Show me the cards so I can see everyone. Why? What is causing your anxiety?
XIV. Homework.
1 level to “3”: page 92 no. 9
Level 2 to 4": page 93 no. 14
Level 3 at “5”: page 96 for ingenuity: Think and try to research and solve this equation yourself 60x + 180 = 420, make a solution plan.
Class: 4
Target: Consider practical ways to solve equations that require more than one arithmetic operation.
Lesson equipment: computer presentation of mental arithmetic, cards with equations, cards of three levels for independent work on tasks, feedback cube
During the classes
1. Organizational moment
Checking readiness for the lesson. The number is written in the notebooks, cool work.
2. Oral counting(computer presentation, slide No. 1)
Game "Snail Competition"
Your favorite dog Alik at the snail competition. Two snails must climb to the top of the mountain. Which one of them will come out first? Our snail is number 1 on the left. The snail takes a step only if we find the meaning of the expression correctly.
You are ready?
The signal to start has already sounded. We repeat the procedure and name the correct meanings of the expressions.
(122 + 18) : 70 = 2
(64: 8 + 20) : 7 = 4
20 · (26 + 14) : 100 = 8
1 (30 + 2) – 4 4 = 16
5 4 + 12 = 32
(400 – 300) – 36 = 64
We have a series of numbers.
2, 4, 8, 16, 32, 64
What pattern did you notice in the compilation of this series? (each subsequent number is doubled)
Continue this series of numbers and name at least the next three numbers. (128, 256, 512…)
Well done! We decided everything correctly, so our snail is on top of the mountain.
Each number has an encrypted letter. Let's turn them over and read the topic of today's lesson.
2 4 8 16 32 64 128 256 512
THE EQUATION
What is the equation called?
What is the root of an equation?
What does it mean to solve an equation?
We already know how to solve simple equations, and today we will get acquainted with solving complex equations where we need to perform several arithmetic operations.
3. Solving simple equations. Preparation for the introduction of new material.
On a magnetic board in random order there are cards with equations.
What groups can all these equations be divided into? (equations are distributed in 3 columns)
1) 7000 – x = 2489
7000 – x = 3489
7000 – x = 1689
Why did we put these equations in the first group? (simple equations With identically reduced) Can we solve them?
Find among them the equation with the largest root and solve it (one student at the board)
2) 71: x = 20 + 7
x: 3 = 16 + 11 ( these are equations on the right side of which the expression)
Can we solve the equations of the second column?
Solve any of the equations, but replace the sum on the right side with the difference. The root of the equation should remain the same. (two students at the blackboard)
3) (490 – x) – 250 = 70
Look at the remaining equation. Is it easy for us to solve it? Why?
4. Working on new material. (frontal conversation with the class, during which the solution to the equation is considered)
(490 – x) – 250 = 70
490 – x = 70 + 250
490 – x = 320
x = 490 – 320
x = 170
(490 – 170) – 250 = 70
70 = 70
Answer: 70
5. Consolidation.
1) Solving the equation (one of the strong students at the blackboard)
5 a + 500 = 4500: 5
5 a + 500 = 900
5 a = 900 – 500
5 a = 400
a = 400: 5
a = 80
5 80 + 500 = 900
900 = 900
Answer: 80
Solve the equations.
A+ 156 = 17 ∙ 20 (1604 – y) – 108 = 800
252: 36 ∙ x = 560 103300: (x + 297) = 25 ∙2
We solved two new complex equations. Look at the equations in front of you. Are they all complex? Which equation is the odd one out? Why? The rest are on the left side an expression in several actions. Find among them a sequence of actions that has already been encountered today.
(1604 – y) – 108 = 800
1604 – y = 800 + 108
1604 – y = 908
y = 1604 – 908
y = 696
(1604 – 696) – 108 = 800
800 = 800
Answer: 696
Solve the equation in pairs. One student turns the board around for later checking.
6. Solving the problem
Independent work using cards of 3 levels. Having completed the task of the first stage, the student proceeds to complete the task of the second stage, then the third.( various ways differentiated work)
Frontal check
1) 25700 – x = 12350
x = 25700 – 12350
x = 13350
25700 – 13350 = 12350
12350 = 12350
Answer: 13350 seedlings.
2) 25700 – x = 12000 + 350
3) 25700 – (x + 8580) = 12350
x + 8580 = 25700 – 12350
x + 8580 = 13350
x = 13350 – 8580
x = 4770
25700 – (4770 + 8580) =12350
12350 = 12350
Answer: 4770 limes.
4) What other equation could be made?
(25700 – x) – 8580 = 12350
We solved three problems by composing three equations. Which equation is considered complex? Why?
7. Homework.
Consider how the equations were solved in the textbook on page 106 and solve the equation in the printed notebook No. 44 (a).
Solve problem No. 47. Additional task: what other questions can be asked about this problem?
8. Lesson summary.
What equations did you learn to solve in class?
Was it difficult?
Who had it easy?
Content:
You can solve simple algebraic equations in just two steps. To do this, it is enough to isolate a variable using addition, subtraction, multiplication or division. Want to know different ways to solve algebraic equations? Read on.
Steps
1 Solving equations with one unknown
- 1 Write down the equations. For solutions algebraic equation First of all, you need to write it down, so everything will immediately become clearer. Let's say we are dealing with the following equation: -4x + 7 = 15.
- 2
We decide what action we will use to isolate the variable. The next step is to figure out how to store "-4x" on one side and constants (integers) on the other. To do this, we use the “law of symmetry” and find the number opposite to +7, this is -7. Now we subtract 7 from both sides of the equation so that the “+7” in the part where the variable is located turns into 0. We simply write “-7” under 7 on one side and under 15 on the other so that the equation essentially does not change.
- We remember Golden Rule algebra. Whatever we do to one side of the equation, we also do to the other. That's why we subtracted 7 from 15 too.
- 3
We add or subtract a constant on both sides of the equation. This way we isolate the variable. Subtracting 7 from +7 we get 0 on the left. Subtracting 7 from +15 we get 8 on the right.
- -4x + 7 = 15 =
- -4x = 8
- 4
By dividing or multiplying we get rid of the coefficient of the variable. In this example the coefficient is -4. To get rid of it you need to divide both sides of the equation by -4.
- Again, all actions are carried out on both sides, which is why you see ÷ -4 twice.
- 5 Find the variable. To do this, divide the left side (-4x) by -4, you get x. Divide the right side of (8) by -4 to get -2. Thus x = -2. The equation is solved in two steps: -- subtraction and division --.
2 Solving equations with variables on both sides
- 1 Write down the equation. We will solve the equation: -2x - 3 = 4x - 15. First, make sure the variables are the same: in this case x.
- 2
Translate the constants to the right side of the equation. To do this you need to use addition or subtraction. The constant is -3, so we take the opposite of +3 and add it to both sides.
- Adding +3 to the left side (-2x -3) we get -2x.
- Adding +3 to the right side (4h -15) we get 4x -12.
- So (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12
- Modified equation: -2x = 4x -12
- 3
We move the variables to the left with a change of sign. We get -6x = -12
- -2x - 4x = (4x - 12) - 4x = -6x = -12
- 4
Finding the variable. To do this, divide both sides by -6 and get x = 2.
- -6x ÷ -6 = -12 ÷ -6
- x = 2
3 Other ways to solve equations in two steps
- 1
The equation can be solved and leaving the variable on the right, it doesn't matter. Let's take the equation 11 = 3 - 7x. First, let's get rid of the 3 on the right, to do this we subtract 3 from both sides. Then divide both sides by -7 and get x:
- 11 = 3 - 7x =
- 11 - 3 = 3 - 3 - 7x =
- 8 = - 7x =
- 8/-7 = -7/7x
- -8/7 = x or -1.14 = x
- 2
We solve the equation by the second action by multiplying, not dividing. The principle is the same. Let's take the equation x/5 + 7 = -3. First, subtract 7 from both sides and then multiply both sides by 5 to get x:
- x/5 + 7 = -3 =
- (x/5 + 7) - 7 = -3 - 7 =
- x/5 = -10
- x/5 * 5 = -10 * 5
- x = -50
Equations
How to solve equations?
In this section we will recall (or study, depending on who you choose) the most elementary equations. So what is the equation? In human language, this is some kind of mathematical expression where there is an equal sign and an unknown. Which is usually denoted by the letter "X". Solve the equation- this is to find such values of x that, when substituted into original expression will give us the correct identity. Let me remind you that identity is an expression that is beyond doubt even for a person who is absolutely not burdened with mathematical knowledge. Like 2=2, 0=0, ab=ab, etc. So how to solve equations? Let's figure it out.
There are all sorts of equations (I’m surprised, right?). But all their infinite variety can be divided into only four types.
4. Other.)
All the rest, of course, most of all, yes...) This includes cubic, exponential, logarithmic, trigonometric and all sorts of others. We will work closely with them in the appropriate sections.
I’ll say right away that sometimes the equations of the first three types they will cheat you so much that you won’t even recognize them... Nothing. We will learn how to unwind them.
And why do we need these four types? And then what linear equations solved in one way square others, fractional rationals - third, A rest They don’t dare at all! Well, it’s not that they can’t decide at all, it’s that I was wrong with mathematics.) It’s just that they have their own special techniques and methods.
But for any (I repeat - for any!) equations provide a reliable and fail-safe basis for solving. Works everywhere and always. This foundation - Sounds scary, but it's very simple. And very (Very!) important.
Actually, the solution to the equation consists of these very transformations. 99% Answer to the question: " How to solve equations?" lies precisely in these transformations. Is the hint clear?)
Identical transformations of equations.
IN any equations To find the unknown, you need to transform and simplify the original example. And so that when changing appearance the essence of the equation has not changed. Such transformations are called identical or equivalent.
Note that these transformations apply specifically to the equations. There are also identity transformations in mathematics expressions. This is another topic.
Now we will repeat all, all, all basic identical transformations of equations.
Basic because they can be applied to any equations - linear, quadratic, fractional, trigonometric, exponential, logarithmic, etc. and so on.
First identity transformation: you can add (subtract) to both sides of any equation any(but one and the same!) number or expression (including an expression with an unknown!). This does not change the essence of the equation.
By the way, you constantly used this transformation, you just thought that you were transferring some terms from one part of the equation to another with a change of sign. Type:
The case is familiar, we move the two to the right, and we get:
![]()
Actually you taken away from both sides of the equation is two. The result is the same:
x+2 - 2 = 3 - 2
Moving terms left and right with a change of sign is simply a shortened version of the first identity transformation. And why do we need such deep knowledge? - you ask. Nothing in the equations. For God's sake, bear it. Just don’t forget to change the sign. But in inequalities, the habit of transference can lead to a dead end...
Second identity transformation: both sides of the equation can be multiplied (divided) by the same thing non-zero number or expression. Here an understandable limitation already appears: multiplying by zero is stupid, and dividing is completely impossible. This is the transformation you use when you solve something cool like
It's clear X= 2. How did you find it? By selection? Or did it just dawn on you? In order not to select and not wait for insight, you need to understand that you are just divided both sides of the equation by 5. When dividing the left side (5x), the five was reduced, leaving pure X. Which is exactly what we needed. And when dividing the right side of (10) by five, the result is, of course, two.
That's all.
It's funny, but these two (only two!) identical transformations are the basis of the solution all equations of mathematics. Wow! It makes sense to look at examples of what and how, right?)
Examples of identical transformations of equations. Main problems.
Let's start with first identity transformation. Transfer left-right.
An example for the younger ones.)
Let's say we need to solve the following equation:
3-2x=5-3x
Let's remember the spell: "with X's - to the left, without X's - to the right!" This spell is instructions for using the first identity transformation.) What expression with an X is on the right? 3x? The answer is incorrect! On our right - 3x! Minus three x! Therefore, when moving to the left, the sign will change to plus. It will turn out:
3-2x+3x=5
So, the X’s were collected in a pile. Let's get into the numbers. There is a three on the left. With what sign? The answer “with none” is not accepted!) In front of the three, indeed, nothing is drawn. And this means that before the three there is plus. So the mathematicians agreed. Nothing is written, which means plus. Therefore, the triple will be transferred to the right side with a minus. We get:
-2x+3x=5-3
There are mere trifles left. On the left - bring similar ones, on the right - count. The answer comes straight away:
In this example, one identity transformation was enough. The second one was not needed. Well, okay.)
An example for older children.)
If you like this site...
By the way, I have a couple more interesting sites for you.)
You can practice solving examples and find out your level. Testing with instant verification. Let's learn - with interest!)
You can get acquainted with functions and derivatives.