Dispute

FormulaCardano

Mostovoy

Odessa

Dispute

Disputes in the Middle Ages always presented an interesting spectacle, attracting idle townspeople, young and old. The topics of the debates were varied, but always scientific. At the same time, science was understood to be what was included in the list of the so-called seven liberal arts, which was, of course, theology. Theological disputes were the most frequent. They argued about everything. For example, about whether to associate a mouse with the holy spirit if it eats the sacrament, whether the Cumae Sibyl could have predicted the birth of Jesus Christ, why the brothers and sisters of the Savior are not canonized, etc.

About the dispute that was supposed to take place between the famous mathematician and the no less famous doctor, only the most general guesses were made, since no one really knew anything. They said that one of them deceived the other (it is unknown who exactly and to whom). Almost all those who gathered in the square had the most vague ideas about mathematics, but everyone was looking forward to the start of the debate. It was always interesting, you could laugh at the loser, regardless of whether he was right or wrong.

When the town hall clock struck five, the gates swung wide open and the crowd rushed inside the cathedral. On either side of the center line connecting the entrance to the altar, two high pulpits were erected near the two side columns, intended for debaters. Those present made a loud noise, not paying any attention to the fact that they were in the church. Finally, in front of the iron grille that separated the iconostasis from the rest of the central nave, a town crier in a black and purple cloak appeared and proclaimed: “Illustrious citizens of the city of Milan! Now the famous mathematician Niccolo Tartaglia from Brenia will speak to you. His opponent was supposed to be the mathematician and physician Geronimo Cardano. Niccolò Tartaglia accuses Cardano of being the last to publish in his book “Ars magna” a method for solving an equation of the 3rd degree, which belongs to him, Tartaglia. However, Cardano himself could not come to the debate and therefore sent his student Luige Ferrari. So, the debate is declared open, its participants are invited to the departments.” An awkward man with a hooked nose and a curly beard climbed onto the pulpit to the left of the entrance, and a young man in his twenties with a handsome, self-confident face ascended to the opposite pulpit. His entire demeanor reflected complete confidence that his every gesture and every word would be received with delight.

Tartaglia began.

Dear Sirs! You know that 13 years ago I managed to find a way to solve an equation of the 3rd degree and then, using this method, I won the dispute with Fiori. My method attracted the attention of your fellow citizen Cardano, and he used all his cunning art to find out the secret from me. He did not stop either from deception or outright forgery. You also know that 3 years ago Cardano’s book on the rules of algebra was published in Nuremberg, where my method, so shamelessly stolen, was made available to everyone. I challenged Cardano and his student to a competition. I proposed to solve 31 problems, the same number was proposed to me by my opponents. A deadline was set for solving problems - 15 days. In 7 days I managed to solve most of the problems that were compiled by Cardano and Ferrari. I printed them and sent them by courier to Milan. However, I had to wait a full five months until I received answers to my tasks. They were resolved incorrectly. This gave me grounds to challenge both of them to a public debate.

Tartaglia fell silent. The young man, looking at the unfortunate Tartaglia, said:

Dear Sirs! My worthy opponent allowed himself, in the very first words of his speech, to express so much slander against me and against my teacher; his argument was so unfounded that it would hardly take me any trouble to refute the first and show you the inconsistency of the second. First of all, what kind of deception can we talk about if Niccolo Tartaglia completely voluntarily shared his method with both of us? And this is how Geronimo Cardano writes about the role of my opponent in the discovery of the algebraic rule. He says that it is not he, Cardano, “but my friend Tartaglia who has the honor of discovering something so beautiful and amazing, surpassing human wit and all the talents of the human spirit. This discovery is truly a heavenly gift, such a wonderful proof of the power of the mind that comprehended it, that nothing can be considered unattainable for him.”

My opponent accused me and my teacher of allegedly giving the wrong solution to his problems. But how can the root of an equation be incorrect if by substituting it into the equation and performing all the actions prescribed in this equation, we arrive at identity? And if Senor Tartaglia wants to be consistent, then he should have responded to the remark why we, who stole, but in his words, his invention and used it to solve the proposed problems, received the wrong solution. We - my teacher and I - do not consider Signor Tartaglia's invention to be of little importance. This invention is wonderful. Moreover, relying largely on it, I found a way to solve an equation of the 4th degree, and in the Ars Magna my teacher talks about this. What does Senor Tartaglia want from us? What is he trying to achieve with the dispute?

Gentlemen, gentlemen,” Tartaglia shouted, “I ask you to listen to me!” I do not deny that my young opponent is very strong in logic and eloquence. But this cannot replace a true mathematical proof. The problems that I gave to Cardano and Ferrari were not solved correctly, but I will prove this too. Indeed, let us take, for example, an equation from among those solved. It is known...

An unimaginable noise arose in the church, completely absorbing the end of the sentence begun by the hapless mathematician. He was not allowed to continue. The crowd demanded that he shut up and that Ferrari should take the turn. Tartaglia, seeing that continuing the argument was completely useless, hastily descended from the pulpit and went out through the northern porch into the square. The crowd wildly greeted the “winner” of the dispute, Luigi Ferrari.

...This is how this dispute ended, which continues to cause more and more new disputes. Who actually owns the method for solving a 3rd degree equation? We're talking now - Niccolo Tartaglie. He discovered it, and Cardano tricked him into making the discovery. And if now we call the formula representing the roots of an equation of the 3rd degree through its coefficients the Cardano formula, then this is a historical injustice. However, is it unfair? How to calculate the degree of participation of each mathematician in the discovery? Maybe over time someone will be able to answer this question absolutely accurately, or maybe it will remain a mystery...

Cardano formula

Using modern mathematical language and modern symbolism, the derivation of Cardano's formula can be found using the following extremely elementary considerations:

Let us be given a general equation of the 3rd degree:

ax 3 +3bx 2 +3cx+d=0 (1)

If you put

, then we give the equation (1) to mind

Let's introduce a new unknown U using equality

By introducing this expression into (2) , we get

hence

If the numerator and denominator of the second term are multiplied by the expression and taken into account, the resulting expression for u turns out to be symmetrical with respect to the signs “+” and “-”, then we finally get

(The product of cubic radicals in the last equality must equal p).

This is the famous Cardano formula. If you go from y back to x, then we obtain a formula that determines the root of a general equation of the 3rd degree.

The young man who treated Tartaglia so mercilessly understood mathematics as easily as he understood the rights of unpretentious secrecy. Ferrari finds a way to solve a 4th degree equation. Cardano included this method in his book. What is this method?

Let (1)

- general equation of 4th degree.

If you put

then the equation (1) can be brought to mind

Where p,q,r- some coefficients depending on a,b,c,d,e. It is easy to see that this equation can be written as follows:

In fact, it is enough to open the brackets, then all terms containing t, cancels out, and we return to the equation (2) .

Let's select a parameter t so that the right side of the equation (3) was a perfect square relative to y. As is known, a necessary and sufficient condition for this is the vanishing of the discriminant of the coefficients of the trinomial (with respect to y) standing on the right:

We have obtained a complete cubic equation, which we can now solve. Let's find any of its roots and add it to the equation (3) , will now take the form

This is a quadratic equation. Solving it, you can find the root of the equation (2) , and therefore (1) .

4 months before his death, Cardano finished his autobiography, which he wrote intensely throughout the last year and which was supposed to sum up his difficult life. He felt death approaching. According to some reports, his own horoscope linked his death with his 75th birthday. He died on September 21, 1576. 2 days before the anniversary. There is a version that he committed suicide in anticipation of imminent death or even to confirm his horoscope. In any case, Cardano the astrologer took the horoscope seriously.

A note about Cardano's formula

Let us analyze the formula for solving the equation in the real domain. So,

When calculating x we have to take the square root first and then the cubic root. We can take the square root while remaining in the real region if . Two square root values that differ in sign appear in different terms for x. The values of the cube root in the real domain are unique and the result is a unique real root x at . By examining the graph of the cubic trinomial, it is easy to verify that it actually has a single real root at . At there are three real roots. When there is a double real root and a single root, and when there is a triple root x=0.

Let's continue studying the formula for . Turns out. What if an equation with integer coefficients has an integer root, when calculating it using the formula, intermediate irrationalities may arise. For example, the equation has a single root (real) - x=1. Cardano's formula gives for this single real root the expression

But virtually any proof involves using the fact that this expression is the root of the equation. If you do not guess this, indestructible cubic radicals will appear during the transformation.

The Cardano-Tartaglia problem was soon forgotten. The formula for solving the cubic equation was associated with the “Great Art” and gradually began to be called formula Cardano.

Many had a desire to restore the true picture of events in a situation where their participants undoubtedly did not tell the whole truth. For many, it was important to establish the extent of Cardano's guilt. By the end of the 19th century, some of the discussions began to take on the character of serious historical and mathematical research. Mathematicians realized what a big role Cardano's work played at the end of the 16th century. It became clear what Leibniz had noted even earlier: “Cardano was a great man with all his shortcomings; without them he would be perfect.”

Simonyan Albina

The work discusses techniques and methods for solving cubic equations. Application of the Cardano formula to solve problems in preparation for the Unified State Exam in mathematics.

Download:

Preview:

Municipal Educational Institution of Children's and Youth Children's and Youth Creativity Palace

Don Academy of Sciences for Young Researchers

Section: Mathematics - Algebra and Number Theory

Research

"Let's take a look into the world of formulas"

on this topic "Solving 3rd degree equations"

Head: mathematics teacher Natalya Alekseevna Babina

G.Salsk 2010

Introduction……………………………………………………………………………….3
Main part……………………………………………………………………………….4
Practical part……………………………………………………………10-13
Conclusion………………………………………………………………………………….14
Literature………………………………………………………………………………………..15
Applications

1. Introduction

Mathematical education received in secondary schools is an essential component of general education and the general culture of modern man. Almost everything that surrounds a person is somehow connected with mathematics. And recent advances in physics, technology, and information technology leave no doubt that in the future the state of affairs will remain the same. Therefore, solving many practical problems comes down to solving various types of equations that you need to learn to solve. We were taught to solve linear equations of the first degree in the first grade, and we did not show much interest in them. More interesting are nonlinear equations - equations of large degrees. Mathematics reveals order, symmetry and certainty, and these are the highest types of beauty.

The goal of my project “Look into the world of formulas” on the topic “Solving cubic equations of the third degree” is to systematize knowledge about how to solve cubic equations, to establish the fact of the existence of a formula for finding the roots of an equation of the third degree, as well as the connection between the roots and coefficients in a cubic equation. In class we solved equations, both cubic and powers higher than 3. Solving equations using different methods, we added, subtracted, multiplied, divided coefficients, raised them to powers and extracted roots from them, in short, we performed algebraic operations. There is a formula for solving quadratic equations. Is there a formula for solving a third degree equation, i.e. instructions in what order and what kind of algebraic operations must be performed with the coefficients in order to obtain the roots. I was interested to know if famous mathematicians had tried to find a general formula suitable for solving cubic equations? And if they tried, were they able to obtain an expression for the roots through the coefficients of the equation?

2. Main part:

In those distant times, when the sages first began to think about equalities containing unknown quantities, there were probably no coins or wallets. In the ancient mathematical problems of Mesopotamia, India, China, Greece, unknown quantities expressed the number of peacocks in the garden, the number of bulls in the herd, and the totality of things taken into account when dividing property. Sources that have reached us indicate that ancient scientists had some general techniques for solving problems with unknown quantities. However, not a single papyrus or clay tablet contains a description of these techniques. An exception is “Arithmetic” by the Greek mathematician Diophantus of Alexandria (III century) - a collection of problems for composing equations with a systematic presentation of their solutions. However, the first manual for solving problems that became widely known was the work of the Baghdad scientist of the 9th century. Muhammad Ben Musa al-Khwarizmi.

This is how I came up with the idea of creating the project “Let’s look into the world of formulas...”, the fundamental questions of this project were:

determining whether there is a formula for solving cubic equations;
in case of a positive answer, search for a formula expressing the roots of a cubic equation through a finite number of algebraic operations on its coefficients.

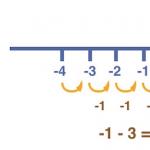
Since in textbooks, and in other books on mathematics, most of the reasoning and proof is carried out not on specific examples, but in general terms, I decided to look for specific examples that confirm or refute my idea. In search of a formula for solving cubic equations, I decided to follow familiar algorithms for solving quadratic equations. For example, solving the equation x 3 + 2x 2 - 5x -6=0 isolated a complete cube using the formula (x+a) 3 =x 3 + 3x 2 a +3a 2 x+a 3 . To isolate the full cube from the left side of the equation I took, I turned 2x in it 2 in 3x 2 and those. I was looking for something so that equality would be fair 2x 2 = 3x 2 a . It was not difficult to calculate that a = . Transformed the left side of this equationas follows: x 3 + 2x 2 -5x-6=0

(x 3 +3x 2 a+ 3x. +) - 3x. - - 5x - 6= (x+) 3 - 6x - 6 Made the substitution y = x +, i.e. x = y - y 3 - 6(y -) - 6=0; 3 - 6y + 4- 6=0; The original equation took the form: y 3 - 6у - 2=0; The result is not a very beautiful equation, because instead of integer coefficients I now have fractional coefficients, although the term in the equation containing the square of the unknown has disappeared! Am I any closer to my goal? After all, the term containing the first degree of the unknown remains. Maybe it was necessary to select the full cube so that the 5x term disappeared? (x+a) 3 =x 3 +3x 2 a+ 3a 2 x + a 3 . I found something like this so that 3a 2 x = -5x; those. so that a 2 = - But here it turned out quite badly - in this equality there is a positive number on the left, and a negative number on the right. There can be no such equality. I have not yet been able to solve the equation; I could only bring it to the form 3 - 6у - 2=0.

So, the result of the work I did at the initial stage: I was able to remove the term containing the second degree from the cubic equation, i.e. if given the canonical equation ax 3 +in 2 +сх+d, then it can be reduced to an incomplete cubic equation x 3 +px+q=0. Further, working with various reference books, I was able to find out that the equation is of the form x 3 + px = q The Italian mathematician Dal Ferro (1465-1526) managed to solve it. Why for this type and not for this type x 3 + px + q = 0? This because negative numbers had not yet been introduced and equations were considered only with positive coefficients. And negative numbers gained recognition a little later.Historical reference:Dal Ferro selected numerous options by analogy with the formula for the roots of the above quadratic equation. He reasoned like this: the root of the quadratic equation is - ± i.e. has the form: x=t ±. This means that the root of a cubic equation must also be the sum or difference of some numbers, and, probably, among them there must be roots of the third degree. Which ones exactly? Of the numerous options, one turned out to be successful: he found the answer in the form of a difference - It was even more difficult to guess that t and u must be chosen so that =. Substituting instead of x the difference - , and instead of p the product received: (-) 3 +3 (-)=q. Opened the brackets: t - 3 +3- u+3- 3=q. After bringing similar terms we got: t-u=q.

The result is a system of equations:

t u = () 3 t-u=q. Let's construct the right and leftsquare the parts of the first equation, and multiply the second equation by 4 and add the first and second equations. 4t 2 +2tu +u 2 =q 2 +4() 3 ; (t+u) 2 =4()+() 3 t+u =2 From the new system t+u=2 ; t -u=q we have: t= + ; u= - . Substituting the expression for x, we gotWhile working on the project, I learned some interesting materials. It turns out that Dal Ferro did not publish the method he found, but some of his students knew about this discovery, and soon one of them, Antonio Fiore, decided to take advantage of it.In those years, public debates on scientific issues were common. The winners of such disputes usually received good rewards and were often invited to high positions.

At the same time, in the Italian city of Verona, there lived a poor mathematics teacher, Nicolo (1499-1557), nicknamed Tartaglia (i.e., the stutterer). He was very talented and managed to rediscover the Dal Ferro technique (Appendix 1).A duel took place between Fiore and Tartaglia. According to the condition, the rivals exchanged thirty problems, the solution of which was given 50 days. But because Fior knew essentially only one problem and was sure that some teacher could not solve it, then all 30 problems turned out to be of the same type. Tartaglia dealt with them in 2 hours. Fiore was unable to solve a single problem proposed by the enemy. The victory glorified Tartaglia throughout Italy, but the issue was not completely resolved. .

Gerolamo Cardano managed to do all this. The very formula that Dal Ferro discovered and rediscovered by Tartaglia is called the Cardano formula (Appendix 2).

Cardano Girolamo (24.9.1501-21.9.1576) - Italian mathematician, mechanic and doctor. Born in Pavia. He studied at the universities of Pavia and Padua. In his youth he studied medicine. In 1534 became a professor of mathematics in Milan and Bologna. In mathematics, the name Cardano is usually associated with a formula for solving a cubic equation, which he borrowed from N. Tartaglia. This formula was published in Cardano's book "The Great Art, or On the Rules of Algebra" (1545). From that time on, Tartaglia and Cardano became mortal enemies. This book systematically presents modern Cardano methods for solving equations, mainly cubic ones. Cardano performed a linear transformation that made it possible to reduce a cubic equation to a form free from a term of the 2nd degree and pointed out the relationship between the roots and coefficients of the equation, and the divisibility of the polynomial by the difference x –a, if a is its root. Cardano was one of the first in Europe to admit the existence of negative roots of equations. In his work, imaginary quantities appear for the first time. In mechanics, Cardano studied the theory of levers and weights. One of the movements of a segment along the sides of a right angle in mechanics is called a carda new movement. So, using the Cardano formula, you can solve equations of the form x 3 +рх+q=0 (Appendix 3)

It seems the problem has been resolved. There is a formula for solving cubic equations.

Here she is!

The expression at the root is discriminant. D = () 2 + () 3 I decided to go back to my equation and try to solve it using the Cardano formula: My equation looks like: y 3 - 6у - 2=0, where p= - 6=-; q = - 2 = - . It's easy to calculate that () 3 = =- and () 2 = =, () 2 + () 3 = = - = - . So what is next? I easily extracted the root from the numerator of this fraction, it turned out to be 15. What to do with the denominator? Not only is the root not completely extracted, but it also needs to be extracted from a negative number! What's the matter? We can assume that this equation has no roots, because for D So, while working on the project, I encountered another problem.What's the matter? I began to compose equations that have roots, but do not contain the term of the square of the unknown:

composed an equation with root x = - 4.

x 3 +15x+124=0 And indeed, by checking I was convinced that -4 is the root of the equation. (-4) 3 +15*(-4)+124=- 64 – 60 +124=0,

I checked whether this root can be obtained using the Cardano formula x=+=+= =1- 5 =- 4

Got it, x = -4.

composed the second equation having a real root x=1: x 3 + 3x – 4 =0 and checked the formula.

And in this case, the formula worked flawlessly.

found the equation x 3 +6x+2=0, which has one irrational root.

Having solved this equation, I got this root x = - And then I had an assumption: the formula worked if the equation had only one root. And my equation, the solution of which drove me into a dead end, had three roots! This is where you need to look for the reason!Now I took an equation that has three roots: 1; 2; -3. x 3 – 7x +6=0 p= -7; q = 6. Checked the discriminant: D = () 2 + () 3 = () 3 + (-) 3 = 9 -

As I assumed, the square root sign again turned out to be a negative number. I came to the conclusion:path to three roots of equation x 3 +px+q=0 leads through the impossible operation of taking the square root of a negative number.

Now I just have to find out what I will encounter in the case when the equation has two roots. I chose an equation that has two roots: x 3 – 12 x + 16 = 0. p = -12, q = 16.

D=() 2 +() 3 =() 2 +() 3 =64-64=0 D = 64 – 64 = 0. Now we could conclude that the number of roots of a cubic equation of the form x 3 +px+q=0 depends on the sign of the discriminant D=() 2 +() 3 in the following way:

If D>0, then the equation has 1 solution.

If D

If D=0, then the equation has 2 solutions.

I found confirmation of my conclusion in a reference book on mathematics, author N.I. Bronshtein. So my conclusion: Cardano's formula can be used when we are sure that the root is unique. To me managed to establish that there is a formula for finding the roots of a cubic equation, but for the form x 3 + px + q = 0.

3. Practical part.

Working on the project “... helped me a lot in solving some problems with parameters. For example:1. For what is the smallest natural value of a the equation x 3 -3x+4=a has 1 solution? The equation was rewritten as x 3 -3x+4-a=0; p= -3; q=4-a. According to the condition, it must have 1 solution i.e. D>0 Let's find D. D=() 2 +(-) 3 = +(-1) 3 = == a 2 -8a+12>0

A (-∞;2) (6; ∞)

The smallest natural value of a from this interval is 1.

Answer. 1

2. At what the largest natural value of the parameter a, the equation x 3 + x 2 -8x+2-a=0 has three roots?

Equation x 3 + 3x 2 -24x+6-3a=0 is reduced to the form y 3 +py+q=0, where a=1; in=3; c=-24; d=6-3a where q= - + and 3 p = q=32-3a; p=-27. For this type of equation D=() 2 + () 3 =() 2 +(-9) 3 = -729 =; D 2 -4 *9* (-1892) = 36864 + 68112 = 324 2 and 1 = ==28, and 2 == - = -7.

+_ . __-___ . _+

7 28

A (-7; 28)

The largest natural value of a from this interval is 28.

Answer.28

3. Depending on the values of parameter a, find the number of roots of the equation x 3 – 3x – a=0

Solution. In the equation p = -3; q = -a. D=() 2 + () 3 =(-) 2 +(-1) 3 = -1=.

_+ . __-__ . _+

For a (-∞;-2) (2;∞) the equation has 1 solution;

When a (-2;2) the equation has 3 roots;

When a = -2; Equation 2 has 2 solutions.

Tests:

1. How many roots do the equations have:

1) x 3 -12x+8=0?

a) 1; b) 2; at 3; d)4

2) x 3 -9x+14=0

a) 1; b) 2; at 3; d)4

2. At what values of p is the equation x 3 +px+8=0 has two roots?

a)3; b) 5; at 3; d)5

Answer: 1.d) 4

2.c) 3.

3.c)-3

The French mathematician Francois Viète (1540-1603) 400 years before us (Appendix 4) was able to establish a connection between the roots of a second-degree equation and their coefficients.

X 1 + x 2 = -p;

X 1 ∙x 2 =q.

I was interested to know: is it possible to establish a connection between the roots of a third-degree equation and their coefficients? If so, what is this connection? This is how my mini-project came into being. I decided to use my existing skills in quadratic equations to solve my problem. I acted by analogy. I took the equation x 3 +px 2 +qx+r =0. If we denote the roots of the equation x 1, x 2, x 3 , then the equation can be written in the form (x-x 1 ) (x-x 2) (x-x 3 )=0 Opening the brackets, we get: x 3 -(x 1 +x 2 +x 3)x 2 +(x 1 x 2 + x 1 x 3 +x 2 x 3)x - x 1 x 2 x 3 =0. We got the following system:

X 1 + x 2 + x 3 = - p;

X 1 x 2 x 3 = - r.

Thus, it is possible to associate the roots of equations of arbitrary degree with their coefficients.What can be learned from Vieta’s theorem in the question that interests me?

1. The product of all the roots of the equation is equal to the modulus of the free term. If the roots of the equation are integers, then they must be divisors of the free term.

Let's go back to the equation x 3 + 2x 2 -5x-6=0. Integers must belong to the set: ±1; ±2; ±3; ±6. Consistently substituting the numbers into the equation, we get the roots: -3; -1; 2.

2. If you solve this equation by factoring, Vieta’s theorem gives a “hint”:It is necessary that when compiling groups for decomposition, numbers appear - divisors of the free term. It is clear that you may not learn right away, because not all divisors are roots of the equation. And, alas, it may not work out at all - after all, the roots of the equation may not be integers.

Let's solve the equation x 3 +2x 2 -5x-6=0 factorization. X 3 +2x 2 -5x-6=x 3 +(3x 2 - x 2)-3x-2x-6=x 2 (x+3)– x(x+3) – 2(x+3)=(x+3)(x 2 –x-2)= =(x+3)(x 2 +x -2x -2)=(x+3)(x(x+1)-2(x+1))=(x+2)(x+1)(x-2) The original equation is equivalent to: ( x+2)(x+1)(x-2)=0. And this equation has three roots: -3;-1;2. Using the “hint” of Vieta’s theorem, I solved the following equation: x 3 -12x+16=0 x 1 x 2 x 3 = -16. Free term divisors: ±1;±2;±4;±8;±16. X 3 -12x+16= x 3 -4x-8x+16= (x 3 -4x)-(8x-16)=x(x 2 -4)-8(x-2)=x(x-2)(x+2)-8(x-2)=

=(x-2)(x(x+2)-8)=(x-2)(x 2 +2x-8) (x-2)(x 2 +2x-8)=0 x-2=0 or x 2 +2x-8=0 x=2 x 1 =-4; x 2 =2. Answer. -4; 2.

3. Knowing the resulting system of equalities, you can find the unknown coefficients of the equation from the roots of the equation.

Tests:

1. Equation x 3 + px 2 + 19x - 12=0 has roots 1, 3, 4. Find the coefficient p; Answer. a) 12; b) 19; at 12; d) -8 2. Equation x 3 – 10 x 2 + 41x +r=0 has roots 2, 3, 5. Find the coefficient r; Answer. a) 19; b) -10; c) 30; d) -30.

Assignments for applying the results of this project in sufficient quantities can be found in the manual for applicants to universities, edited by M.I. Skanavi. Knowledge of Vieta's theorem can be of invaluable help in solving such problems.

№6.354

4. Conclusion

1. There is a formula expressing the roots of an algebraic equation through the coefficients of the equation: where D==() 2 + () 3 D>0, 1 solution. Cardano formula.

2. Property of the roots of the cubic equation

X 1 + x 2 + x 3 = - p;

X 1. x 2 + x 1 x 3 + x 2 x 3 = q;

X 1 x 2 x 3 = - r.

As a result, I came to the conclusion that there is a formula that expresses the roots of cubic equations through its coefficients, and there is also a connection between the roots and coefficients of the equation.

5. Literature:

1. Encyclopedic dictionary of a young mathematician. A.P. Savin. –M.: Pedagogy, 1989.

2.Unified state exam in mathematics - 2004. Problems and solutions. V.G.Agakov, N.D.Polyakov, M.P.Urukova and others. Cheboksary. Publishing house Chuvash. University, 2004.

3.Equations and inequalities with parameters. V.V. Mochalov, V.V. Silvestrov Equations and inequalities with parameters: Textbook. allowance. – Cheboksary: Chuvash Publishing House. Univ., 2004.

4.Mathematics problems. Algebra. Reference manual. Vavilov V.V., Olehnik S.N.-M.: Nauka, 1987.

5. Solver of all competitive problems in mathematics, collection edited by M.I. Skanavi. Publishing house "Ukrainian Encyclopedia" named after M.P. Bazhov, 1993.

6.Behind the pages of an algebra textbook. L.F.Pichurin.-M.: Education, 1990.

Preview:

To use presentation previews, create a Google account and log in to it: https://accounts.google.com

Slide captions:

Let's take a look into the world of formulas

the equation has the form (1) we transform the equation so as to isolate the exact cube: we multiply (1) the equations by 3 (2) we transform (2) the equations we get the following equation we raise the right and left sides of (3) of the equation to the third power we find the roots of the equation Examples of solutions cubic equations

Quadratic equations of the form where the discriminant There are no roots among the real numbers

Third degree equation

Historical background: In those distant times, when the sages first began to think about equalities containing unknown quantities, there were probably no coins or wallets. In the ancient mathematical problems of Mesopotamia, India, China, Greece, unknown quantities expressed the number of peacocks in the garden, the number of bulls in the herd, and the totality of things taken into account when dividing property. Sources that have reached us indicate that ancient scientists had some general techniques for solving problems with unknown quantities. However, not a single papyrus or clay tablet contains a description of these techniques. An exception is “Arithmetic” by the Greek mathematician Diophantus of Alexandria (III century) - a collection of problems for composing equations with a systematic presentation of their solutions. However, the first manual for solving problems that became widely known was the work of the Baghdad scientist of the 9th century. Muhammad Ben Musa al-Khwarizmi.

the equation has the form (1) apply formula 1) by selecting find and so that the following equality holds, we transform the left side of (1) the equation as follows: selecting the complete cube, take the sum as y, we obtain an equation for y (2) simplify (2) equation ( 3) In (3) the term containing the square of the unknown disappeared, but the term containing the first degree of the unknown remained 2) by selection, find and so that the following equality holds. Such an equality is impossible since there is a positive number on the left and a negative number on the left. If we follow this path then we will get stuck... We will fail on our chosen path. We cannot solve the equation yet.

Cubic equations are equations of the form where (1) 1. Let us simplify the equations by dividing them by a, then the coefficient of “x” becomes equal to 1, therefore the solution of any cubic equation is based on the sum cube formula: (2) if we take then equation (1) differs from the equation (2) only by the coefficient of x and the free term. Let's add up equations (1) and (2) and present similar ones: if we make a substitution here, we get a cubic equation for y without a term:

Cardano Girolamo

Cardano Girolamo (24.9.1501-21.9.1576) - Italian mathematician, mechanic and doctor. Born in Pavia. He studied at the universities of Pavia and Padua. In his youth he studied medicine. In 1534 became a professor of mathematics in Milan and Bologna. In mathematics, the name Cardano is usually associated with a formula for solving a cubic equation, which he borrowed from N. Tartaglia. This formula was published in Cardano's book "The Great Art, or On the Rules of Algebra" (1545). From that time on, Tartaglia and Cardano became mortal enemies. This book systematically presents modern Cardano methods for solving equations, mainly cubic ones. Cardano performed a linear transformation that made it possible to reduce a cubic equation to a form free from a term of the 2nd degree; he pointed out the relationship between the roots and coefficients of the equation, and the divisibility of the polynomial by the difference x –a, if a is its root. Cardano was one of the first in Europe to admit the existence of negative roots of equations. In his work, imaginary quantities appear for the first time. In mechanics, Cardano studied the theory of levers and weights. One of the movements of a segment along the sides of a right angle of mechanics is called cardan movement. Biography of Cardano Girolamo

At the same time, in the Italian city of Verona, there lived a poor mathematics teacher, Nicolo (1499-1557), nicknamed Tartaglia (i.e., the stutterer). He was very talented and managed to rediscover the Dal Ferro technique. A duel took place between Fiore and Tartaglia. According to the condition, the rivals exchanged 30 problems, the solution of which was given 50 days. But since Fior essentially knew only one problem and was sure that some teacher could not solve it, all 30 problems turned out to be of the same type. Tartaglia dealt with them in two hours. Fiore was unable to solve a single problem proposed by the enemy. The victory made Tartaglia famous throughout Italy, but the issue was not completely resolved. The simple technique with which we were able to cope with a member of the equation containing a square of an unknown value (selecting a complete cube) had not yet been discovered and the solution to equations of various types was not was brought into the system. Fiore's duel with Tartaglia

an equation of the form from a given equation and let's calculate the discriminant of the equation Not only is the root of this equation not extracted entirely, but it also needs to be extracted from a negative number. What's the matter? We can assume that this equation has no roots, because D

The roots of a cubic equation depend on the discriminant the equation has 1 solution the equation has 3 solutions the equation has 2 solutions Conclusion

the equation has the form: find the roots of the equation using the Cardano formula Examples of solving cubic equations using the Cardano formula

an equation of the form (1) from the given equation and since, by condition, this equation must have 1 solution, then Calculate the discriminant (1) of the equation + - + 2 6 Answer: the smallest natural value of a from this interval is 1 At what is the smallest natural value of a the equation has 1 solution?

Solving cubic equations using the Vieta method The equations have the form

Solve an equation if it is known that the product of its two roots is equal to 1 by Vieta’s theorem and the condition we have or substitute the value into the first equation or substitute the value from the third equation into the first we get the roots of the equation or Answer:

Literature used: “Mathematics. Educational and methodological manual » Yu.A. Gusman, A.O. Smirnov. Encyclopedia “I explore the world. Mathematics" - Moscow, AST, 1996. " Mathematics. Educational and methodological manual » V.T. Lisichkin. A manual for applicants to universities, edited by M.I. Skanavi. Unified State Examination in Mathematics - 2004.

Thank you for your attention

Any cubic equation with real coefficients has at least one real root, the other two are either also real or are a complex conjugate pair.

Let's start the review with the simplest cases - binomial And returnable equations. Then we move on to finding rational roots (if any). Let's finish with an example of finding the roots of a cubic equation using Cardano's formula for the general case.

Page navigation.

Solving a two-term cubic equation.

The binomial cubic equation has the form .

This equation is reduced to the form by dividing by a coefficient A that is different from zero. Next, apply the formula for abbreviated multiplication sum of cubes:

From the first bracket we find , and the square trinomial has only complex roots.

Example.

Find the real roots of the cubic equation.

Solution.

We apply the formula for abbreviated multiplication of difference of cubes:

From the first bracket we find that the square trinomial in the second bracket has no real roots, since its discriminant is negative.

Answer:

Solving the reciprocal cubic equation.

The reciprocal cubic equation has the form , where A and B are coefficients.

Let's group:

Obviously, x = -1 is the root of such an equation, and the roots of the resulting quadratic trinomial are easily found through the discriminant.

Example.

Solve cubic equation .

Solution.

This is a reciprocal equation. Let's group:

Obviously x = -1 is the root of the equation.

Finding the roots of a quadratic trinomial:

Answer:

Solving cubic equations with rational roots.

Let's start with the simplest case, when x=0 is the root of the cubic equation.

In this case, the free term D is equal to zero, that is, the equation has the form .

If you take x out of brackets, then a square trinomial will remain in brackets, the roots of which can be easily found either through the discriminant or by Vieta’s theorem .

Example.

Find the real roots of the equation .

Solution.

x=0 is the root of the equation. Let's find the roots of the quadratic trinomial.

Since its discriminant is less than zero, the trinomial has no real roots.

Answer:

x=0.

If the coefficients of a cubic equation are integers, then the equation can have rational roots.

When , multiply both sides of the equation by and change variables y = Ax:

We arrived at the given cubic equation. It can have whole roots, which are divisors of the free term. So we write down all the divisors and begin to substitute them into the resulting equation until we obtain an identical equality. The divisor at which the identity is obtained is the root of the equation. Therefore, the root of the original equation is .

Example.

Find the roots of the cubic equation.

Solution.

Let's transform the equation to the above: multiply by both sides and change the variable y = 2x.

The free term is 36. Let's write down all its divisors: .

We substitute them one by one into equality until identity is obtained:

So y = -1 is the root. It corresponds to .

Let's divide on, using:

We get

All that remains is to find the roots of the quadratic trinomial.

It's obvious that , that is, its multiple root is x=3.

Answer:

Comment.

This algorithm can be used to solve reciprocal equations. Since -1 is the root of any reciprocal cubic equation, we can divide the left side of the original equation by x+1 and find the roots of the resulting quadratic trinomial.

In the case when the cubic equation does not have rational roots, other solution methods are used, for example, specific methods.

Solving cubic equations using the Cardano formula.

In general, the roots of a cubic equation are found using the Cardano formula.

For the cubic equation the values are found . Next we find And .

We substitute the resulting p and q into the Cardano formula:

MUNICIPAL VII STUDENT SCIENTIFIC AND PRACTICAL CONFERENCE “YOUTH: CREATIVITY, SEARCH, SUCCESS”

Anninsky municipal district

Voronezh region

Section:MATHEMATICS

Subject:"Cardano Formula: History and Application"

MKOU Anninskaya secondary school No. 3, 9 “B” class

Niccolò Fontana Tartaglia (Italian: NiccolòFontanaTartaglia, 1499-1557) - Italian mathematician.

In general, history tells that the formula was initially discovered by Tartaglia and handed over to Cardano in finished form, but Cardano himself denied this fact, although he did not deny Tartaglia’s involvement in the creation of the formula.

The name “Cardano’s formula” is firmly rooted behind the formula, in honor of the scientist who actually explained and presented it to the public.

When the town hall clock struck five, the gates swung wide open and the crowd rushed inside the cathedral. On either side of the center line connecting the entrance to the altar, two high pulpits were erected near the two side columns, intended for debaters. Those present made a loud noise, not paying any attention to the fact that they were in the church. Finally, in front of the iron grille that separated the iconostasis from the rest of the central nave, a town crier in a black and purple cloak appeared and proclaimed: “Illustrious citizens of the city of Milan! Now the famous mathematician Niccolo Tartaglia from Brenia will speak to you. His opponent was supposed to be the mathematician and physician Geronimo Cardano. Niccolò Tartaglia accuses Cardano of the fact that the latter, in his book “Arsmagna,” published a method for solving an equation of the 3rd degree, which belongs to him, Tartaglia. However, Cardano himself could not come to the debate and therefore sent his student Luige Ferrari. So, the debate is declared open, its participants are invited to the departments.” An awkward man with a hooked nose and a curly beard climbed onto the pulpit to the left of the entrance, and a young man in his twenties with a handsome, self-confident face ascended to the opposite pulpit. His entire demeanor reflected complete confidence that his every gesture and every word would be received with delight.

Tartaglia began.

Tartaglia fell silent. The young man, looking at the unfortunate Tartaglia, said:

My opponent accused me and my teacher of allegedly giving the wrong solution to his problems. But how can the root of an equation be incorrect if by substituting it into the equation and performing all the actions prescribed in this equation, we arrive at identity? And if Senor Tartaglia wants to be consistent, then he should have responded to the remark why we, who, in his words, stole his invention and used it to solve the proposed problems, received the wrong solution. We - my teacher and I - do not consider Signor Tartaglia's invention to be of little importance. This invention is wonderful. Moreover, relying largely on it, I found a way to solve an equation of the 4th degree, and in Arsmagna my teacher talks about this. What does Senor Tartaglia want from us? What is he trying to achieve with the dispute?

Gentlemen, gentlemen,” Tartaglia shouted, “I ask you to listen to me!” I do not deny that my young opponent is very strong in logic and eloquence. But this cannot replace a true mathematical proof. The problems I gave to Cardano and Ferrari were solved incorrectly, but I will prove it too. Indeed, let us take, for example, an equation from among those solved. It is known...

Thus ended this dispute, which continues to cause more and more new disputes. Who actually owns the method for solving a 3rd degree equation? We're talking now - Niccolo Tartaglie. He discovered it, and Cardano tricked him into making the discovery. And if now we call the formula representing the roots of an equation of the 3rd degree through its coefficients the Cardano formula, then this is a historical injustice. However, is it unfair? How to calculate the degree of participation of each mathematician in the discovery? Maybe over time someone will be able to answer this question absolutely accurately, or maybe it will remain a mystery...

Using modern mathematical language and modern symbolism, the derivation of Cardano's formula can be found using the following extremely elementary considerations:

Let us be given a general equation of the 3rd degree:

x 3 + ax 2 + bx + c = 0,

(1)

Wherea, b, c – arbitrary real numbers.

Let us replace the variable in equation (1)X to a new variable yaccording to the formula:

x 3 +ax 2 +bx+c = (y ) 3 + a(y ) 2 + b(y ) + c = y 3 3y 2 + 3y+ a(y 2 2y+ by = y 3 y 3 + (b

then equation (1) will take the formy 3 + ( b

If we introduce the notationp = b, q = ,

then the equation will take the formy 3 + py + q = 0.

This is the famous Cardano formula.

Roots of a cubic equationy 3 + py + q = 0 depend on the discriminant

IfD> 0, thena cubic polynomial has three different real roots.

IfD< 0, то a cubic polynomial has one real root and two complex roots (which are complex conjugate).

IfD = 0, it has a multiple root (either one root of multiplicity 2 and one root of multiplicity 1, both of which are real; or one single real root of multiplicity 3).

2.4. Examples of universal methods for solving cubic equations

Let's try to apply Cardan's formula to solving specific equations.

Example 1: x 3 +15 x+124 = 0

Herep = 15; q = 124.

Answer:X