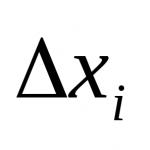Ilya's answer is correct, but not very detailed. In the 18th century, by the way, one was still considered a prime number. For example, such great mathematicians as Euler and Goldbach. Goldbach is the author of one of the seven problems of the millennium - the Goldbach hypothesis. The original formulation states that any even number representable as the sum of two prime numbers. Moreover, initially 1 was taken into account as a prime number, and we see this: 2 = 1+1. This smallest example, satisfying the original formulation of the hypothesis. Later it was corrected, and the formulation acquired a modern form: “every even number, starting with 4, can be represented as the sum of two prime numbers.”
Let's remember the definition. Simple is natural number p, having only 2 different natural divisors: p itself and 1. Corollary from the definition: a prime number p has only one prime divisor - p itself.
Now let's assume that 1 is a prime number. By definition, a prime number has only one prime divisor - itself. Then it turns out that any prime number greater than 1 is divisible by a prime number different from it (by 1). But two different prime numbers cannot be divided by each other, because otherwise they are not prime numbers, but composite numbers, and this contradicts the definition. With this approach, it turns out that there is only 1 prime number - the unit itself. But this is absurd. Therefore, 1 is not a prime number.
1, as well as 0, form another class of numbers - the class of neutral elements with respect to n-ary operations in some subset of the algebraic field. Moreover, with respect to the operation of addition, 1 is also a generating element for the ring of integers.
With this consideration, it is not difficult to discover analogues of prime numbers in other algebraic structures. Suppose we have a multiplicative group formed from powers of 2, starting from 1: 2, 4, 8, 16, ... etc. 2 acts as a formative element here. A prime number in this group is a number greater than the smallest element and divisible only by itself and the smallest element. In our group, only 4 have such properties. That’s it. There are no more prime numbers in our group.
If 2 were also a prime number in our group, then see the first paragraph - again it would turn out that only 2 is a prime number.
Definition 1. Prime number− is a natural number greater than one that is divisible only by itself and 1.
In other words, a number is prime if it has only two distinct natural divisors.
Definition 2. Any natural number that has other divisors besides itself and one is called a composite number.
In other words, natural numbers that are not prime numbers are called composite numbers. From Definition 1 it follows that composite number has more than two natural divisors. The number 1 is neither prime nor composite because has only one divisor 1 and, in addition, many theorems regarding prime numbers do not hold for unity.
From Definitions 1 and 2 it follows that every positive integer greater than 1 is either a prime number or a composite number.
Below is a program to display prime numbers up to 5000. Fill in the cells, click on the "Create" button and wait a few seconds.
Prime numbers table
Statement 1. If p- prime number and a any integer, then either a divided by p, or p And a coprime numbers.
Really. If p A prime number is divisible only by itself and 1 if a not divisible by p, then the greatest common divisor a And p is equal to 1. Then p And a coprime numbers.
Statement 2. If the product of several numbers of numbers a 1 , a 2 , a 3, ... is divisible by a prime number p, then at least one of the numbers a 1 , a 2 , a 3, ...divisible by p.
Really. If none of the numbers were divisible by p, then the numbers a 1 , a 2 , a 3, ... would be coprime numbers with respect to p. But from Corollary 3 () it follows that their product a 1 , a 2 , a 3, ... is also relatively prime with respect to p, which contradicts the condition of the statement. Therefore at least one of the numbers is divisible by p.
Theorem 1. Any composite number can always be represented, and in a unique way, as the product of a finite number of prime numbers.
Proof. Let k composite number, and let a 1 is one of its divisors different from 1 and itself. If a 1 is composite, then has in addition to 1 and a 1 and another divisor a 2. If a 2 is a composite number, then it has, in addition to 1 and a 2 and another divisor a 3. Reasoning in this way and taking into account that the numbers a 1 , a 2 , a 3 , ... decrease and this series contains a finite number of terms, we will reach some prime number p 1 . Then k can be represented in the form
Suppose there are two decompositions of a number k:
Because k=p 1 p 2 p 3...divisible by a prime number q 1, then at least one of the factors, for example p 1 is divisible by q 1 . But p 1 is a prime number and is only divisible by 1 and itself. Hence p 1 =q 1 (because q 1 ≠1)
Then from (2) we can exclude p 1 and q 1:
Thus, we are convinced that every prime number that appears as a factor in the first expansion one or more times also appears in the second expansion at least as many times, and vice versa, any prime number that appears as a factor in the second expansion one or more times also appears in the first expansion at least the same number of times. Therefore, any prime number is included as a factor in both expansions same number times and thus these two expansions are the same.■
Expansion of a composite number k can be written in the following form
| (3) |
Where p 1 , p 2, ... various prime numbers, α, β, γ ... positive integers.
Expansion (3) is called canonical expansion numbers.
Prime numbers occur unevenly in the series of natural numbers. In some parts of the row there are more of them, in others - less. The further we move along number series, the less common prime numbers are. The question arises, is there a largest prime number? The ancient Greek mathematician Euclid proved that there are infinitely many prime numbers. We present this proof below.
Theorem 2. The number of prime numbers is infinite.
Proof. Suppose there are a finite number of prime numbers, and let the largest prime number be p. Let's consider all numbers greater p. By assumption of the statement, these numbers must be composite and must be divisible by at least one of the prime numbers. Let's choose a number that is the product of all these prime numbers plus 1:
Number z more p because 2p already more p. p is not divisible by any of these prime numbers, because when divided by each of them gives a remainder of 1. Thus we come to a contradiction. Therefore there are an infinite number of prime numbers.
This theorem is a special case of a more general theorem:
Theorem 3. Let an arithmetic progression be given
Then any prime number included in n, should be included in m, therefore in n others cannot enter prime factors, which are not included in m and, moreover, these prime factors in n are included no more times than in m.
The opposite is also true. If every prime factor of a number n included at least as many times in the number m, That m divided by n.
Statement 3. Let a 1 ,a 2 ,a 3,... various prime numbers included in m So
Where i=0,1,...α , j=0,1,...,β , k=0,1,..., γ . notice, that αi accepts α +1 values, β j accepts β +1 values, γ k accepts γ +1 values, ... .
In this article we will explore prime and composite numbers. First, we will give definitions of prime and composite numbers, and also give examples. After this we will prove that there are infinitely many prime numbers. Next, we will write down a table of prime numbers, and consider methods for compiling a table of prime numbers, paying particular attention to the method called the sieve of Eratosthenes. In conclusion, we will highlight the main points that need to be taken into account when proving that a given number is prime or composite.
Page navigation.
Prime and Composite Numbers - Definitions and Examples
The concepts of prime numbers and composite numbers refer to numbers that are greater than one. Such integers, depending on the number of their positive divisors, are divided into prime and composite numbers. So to understand definitions of prime and composite numbers, you need to have a good understanding of what divisors and multiples are.
Definition.
Prime numbers are integers, large units, that have only two positive divisors, namely themselves and 1.
Definition.
Composite numbers are integers, large ones, that have at least three positive divisors.
Separately, we note that the number 1 does not apply to either prime or composite numbers. Unit has only one positive divisor, which is the number 1 itself. This distinguishes the number 1 from all other positive integers that have at least two positive divisors.
Considering that positive integers are , and that one has only one positive divisor, we can give other formulations of the stated definitions of prime and composite numbers.
Definition.
Prime numbers are natural numbers that have only two positive divisors.
Definition.
Composite numbers are natural numbers that have more than two positive divisors.
Note that every positive integer greater than one is either a prime or a composite number. In other words, there is not a single integer that is neither prime nor composite. This follows from the property of divisibility, which states that the numbers 1 and a are always divisors of any integer a.
Based on the information in the previous paragraph, we can give the following definition of composite numbers.
Definition.
Natural numbers that are not prime are called composite.
Let's give examples of prime and composite numbers.
Examples of composite numbers include 6, 63, 121, and 6,697. This statement also needs clarification. The number 6, in addition to positive divisors 1 and 6, also has divisors 2 and 3, since 6 = 2 3, therefore 6 is truly a composite number. Positive factors of 63 are the numbers 1, 3, 7, 9, 21 and 63. The number 121 is equal to the product 11·11, so its positive divisors are 1, 11 and 121. And the number 6,697 is composite, since its positive divisors, in addition to 1 and 6,697, are also the numbers 37 and 181.
In conclusion of this point, I would also like to draw attention to the fact that prime numbers and coprime numbers are far from the same thing.
Prime numbers table
Prime numbers, for the convenience of their further use, are recorded in a table called a table of prime numbers. Below is prime numbers table up to 1,000.
A logical question arises: “Why did we fill the table of prime numbers only up to 1,000, isn’t it possible to create a table of all existing prime numbers”?
Let's answer the first part of this question first. For most problems that require the use of prime numbers, prime numbers within a thousand will be sufficient. In other cases, most likely, you will have to resort to some special solutions. Although we can certainly create a table of prime numbers up to an arbitrarily large finite positive integer, be it 10,000 or 1,000,000,000, in the next paragraph we will talk about methods for creating tables of prime numbers, in particular, we will look at a method called.
Now let's look at the possibility (or rather, the impossibility) of compiling a table of all existing prime numbers. We cannot make a table of all the prime numbers because there are infinitely many prime numbers. The last statement is a theorem that we will prove after the following auxiliary theorem.
Theorem.
The smallest positive divisor other than 1 of a natural number greater than one is a prime number.
Proof.
Let a is a natural number greater than one, and b is the smallest positive divisor of a other than one. Let us prove that b is a prime number by contradiction.
Let's assume that b is a composite number. Then there is a divisor of the number b (let's denote it b 1), which is different from both 1 and b. If we also take into account that the absolute value of the divisor does not exceed absolute value divisible (we know this from the properties of divisibility), then condition 1 must be satisfied
Since the number a is divisible by b according to the condition, and we said that b is divisible by b 1, the concept of divisibility allows us to talk about the existence of integers q and q 1 such that a=b q and b=b 1 q 1 , from where a= b 1 ·(q 1 ·q) . It follows that the product of two integers is an integer, then the equality a=b 1 ·(q 1 ·q) indicates that b 1 is a divisor of the number a. Taking into account the above inequalities 1
Now we can prove that there are infinitely many prime numbers.
Theorem.
There are an infinite number of prime numbers.
Proof.
Let's assume that this is not the case. That is, suppose that there are only n prime numbers, and these prime numbers are p 1, p 2, ..., p n. Let us show that we can always find a prime number different from those indicated.
Consider the number p equal to p 1 ·p 2 ·…·p n +1. It is clear that this number is different from each of the prime numbers p 1, p 2, ..., p n. If the number p is prime, then the theorem is proven. If this number is composite, then by virtue of the previous theorem there is a prime divisor of this number (we denote it p n+1). Let us show that this divisor does not coincide with any of the numbers p 1, p 2, ..., p n.
If this were not so, then, according to the properties of divisibility, the product p 1 ·p 2 ·…·p n would be divided by p n+1. But the number p is also divisible by p n+1, equal to the sum p 1 ·p 2 ·…·p n +1. It follows that p n+1 must divide the second term of this sum, which is equal to one, but this is impossible.
Thus, it has been proven that a new prime number can always be found that is not included among any number of predetermined prime numbers. Therefore, there are infinitely many prime numbers.
So, due to the fact that there are an infinite number of prime numbers, when compiling tables of prime numbers, you always limit yourself from above to some number, usually 100, 1,000, 10,000, etc.
Sieve of Eratosthenes
Now we will discuss ways to create tables of prime numbers. Suppose we need to make a table of prime numbers up to 100.
The most obvious method for solving this problem is to sequentially check positive integers, starting from 2 and ending with 100, for the presence of a positive divisor that is greater than 1 and less than the number being tested (from the properties of divisibility we know that the absolute value of the divisor does not exceed the absolute value of the dividend, non-zero). If such a divisor is not found, then the number being tested is prime, and it is entered into the prime numbers table. If such a divisor is found, then the number being tested is composite; it is NOT entered in the table of prime numbers. After this, there is a transition to the next number, which is similarly checked for the presence of a divisor.
Let's describe the first few steps.
We start with the number 2. The number 2 has no positive divisors other than 1 and 2. Therefore, it is simple, therefore, we enter it in the table of prime numbers. Here it should be said that 2 is the smallest prime number. Let's move on to number 3. Its possible positive divisor other than 1 and 3 is the number 2. But 3 is not divisible by 2, therefore, 3 is a prime number, and it also needs to be included in the table of prime numbers. Let's move on to number 4. Its positive divisors other than 1 and 4 can be the numbers 2 and 3, let's check them. The number 4 is divisible by 2, therefore, 4 is a composite number and does not need to be included in the table of prime numbers. Please note that 4 is the smallest composite number. Let's move on to number 5. We check whether at least one of the numbers 2, 3, 4 is its divisor. Since 5 is not divisible by 2, 3, or 4, then it is prime, and it must be written down in the table of prime numbers. Then there is a transition to the numbers 6, 7, and so on up to 100.
This approach to compiling a table of prime numbers is far from ideal. One way or another, he has a right to exist. Note that with this method of constructing a table of integers, you can use divisibility criteria, which will slightly speed up the process of finding divisors.
There is a more convenient way to create a table of prime numbers, called. The word “sieve” present in the name is not accidental, since the actions of this method help, as it were, to “sift” whole numbers and large units through the sieve of Eratosthenes in order to separate simple ones from composite ones.
Let's show the sieve of Eratosthenes in action when compiling a table of prime numbers up to 50.
First, write down the numbers 2, 3, 4, ..., 50 in order.

The first number written, 2, is prime. Now, from number 2, we sequentially move to the right by two numbers and cross out these numbers until we reach the end of the table of numbers being compiled. This will cross out all numbers that are multiples of two.

The first number following 2 that is not crossed out is 3. This number is prime. Now, from number 3, we sequentially move to the right by three numbers (taking into account the already crossed out numbers) and cross them out. This will cross out all numbers that are multiples of three.

The first number following 3 that is not crossed out is 5. This number is prime. Now from the number 5 we consistently move to the right by 5 numbers (we also take into account the numbers crossed out earlier) and cross them out. This will cross out all numbers that are multiples of five.

Next, we cross out numbers that are multiples of 7, then multiples of 11, and so on. The process ends when there are no more numbers to cross off. Below is the completed table of prime numbers up to 50, obtained using the sieve of Eratosthenes. All uncrossed numbers are prime, and all crossed out numbers are composite.

Let's also formulate and prove a theorem that will speed up the process of compiling a table of prime numbers using the sieve of Eratosthenes.
Theorem.
The smallest positive divisor of a composite number a that is different from one does not exceed , where is from a .
Proof.
Let us denote by the letter b the smallest divisor of a composite number a that is different from one (the number b is prime, as follows from the theorem proven at the very beginning of the previous paragraph). Then there is an integer q such that a=b·q (here q is a positive integer, which follows from the rules of multiplication of integers), and (for b>q the condition that b is the least divisor of a is violated, since q is also a divisor of the number a due to the equality a=q·b ). By multiplying both sides of the inequality by a positive and an integer greater than one (we are allowed to do this), we obtain , from which and .
What does the proven theorem give us regarding the sieve of Eratosthenes?
Firstly, crossing out composite numbers that are multiples of a prime number b should begin with a number equal to (this follows from the inequality). For example, crossing out numbers that are multiples of two should begin with the number 4, multiples of three with the number 9, multiples of five with the number 25, and so on.
Secondly, compiling a table of prime numbers up to the number n using the sieve of Eratosthenes can be considered complete when all composite numbers that are multiples of prime numbers not exceeding . In our example, n=50 (since we are making a table of prime numbers up to 50) and, therefore, the sieve of Eratosthenes should eliminate all composite numbers that are multiples of the prime numbers 2, 3, 5 and 7 that do not exceed the arithmetic square root of 50. That is, we no longer need to search for and cross out numbers that are multiples of prime numbers 11, 13, 17, 19, 23 and so on up to 47, since they will already be crossed out as multiples of smaller prime numbers 2, 3, 5 and 7 .
Is this number prime or composite?
Some tasks require finding out whether a given number is prime or composite. In general, this task is far from simple, especially for numbers whose writing consists of a significant number of characters. In most cases, you have to look for some specific way to solve it. However, we will try to give direction to the train of thought for simple cases.
Of course, you can try to use divisibility tests to prove that a given number is composite. If, for example, some test of divisibility shows that a given number is divisible by some positive integer greater than one, then the original number is composite.
Example.
Prove that 898,989,898,989,898,989 is a composite number.
Solution.
The sum of the digits of this number is 9·8+9·9=9·17. Since the number equal to 9·17 is divisible by 9, then by divisibility by 9 we can say that the original number is also divisible by 9. Therefore, it is composite.
A significant drawback of this approach is that the divisibility criteria do not allow one to prove the primeness of a number. Therefore, when testing a number to see whether it is prime or composite, you need to proceed differently.
The most logical approach is to try all possible divisors of a given number. If none of the possible divisors is a true divisor of a given number, then this number will be prime, otherwise it will be composite. From the theorems proved in the previous paragraph, it follows that divisors of a given number a must be sought among prime numbers not exceeding . Thus, a given number a can be sequentially divided by prime numbers (which are conveniently taken from the table of prime numbers), trying to find the divisor of the number a. If a divisor is found, then the number a is composite. If among the prime numbers not exceeding , there is no divisor of the number a, then the number a is prime.
Example.
Number 11 723 simple or compound?
Solution.
Let's find out up to what prime number the divisors of the number 11,723 can be. To do this, let's evaluate.
It's pretty obvious that ![]() , since 200 2 =40,000, and 11,723<40 000
(при необходимости смотрите статью comparison of numbers). Thus, the possible prime factors of 11,723 are less than 200. This already makes our task much easier. If we didn’t know this, then we would have to go through all the prime numbers not up to 200, but up to the number 11,723.
, since 200 2 =40,000, and 11,723<40 000
(при необходимости смотрите статью comparison of numbers). Thus, the possible prime factors of 11,723 are less than 200. This already makes our task much easier. If we didn’t know this, then we would have to go through all the prime numbers not up to 200, but up to the number 11,723.
If desired, you can evaluate more accurately. Since 108 2 =11,664, and 109 2 =11,881, then 108 2<11 723<109 2
, следовательно, ![]() . Thus, any of the prime numbers less than 109 is potentially a prime factor of the given number 11,723.
. Thus, any of the prime numbers less than 109 is potentially a prime factor of the given number 11,723.
Now we will sequentially divide the number 11,723 into prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 , 73 , 79 , 83 , 89 , 97 , 101 , 103 , 107 . If the number 11,723 is divided by one of the written prime numbers, then it will be composite. If it is not divisible by any of the written prime numbers, then the original number is prime.
We will not describe this whole monotonous and monotonous process of division. Let's say right away that 11,723
Is one a prime number? No, one is not a prime number.
Is 0 a prime number? No, zero is not a prime number.
Is 2 a prime number? Yes, 2 is a prime number. 2 is the only even prime number.
Is 3 a prime number? Yes, 3 is a prime number.
Is 5 a prime number? Yes, 5 is a prime number.
Is 7 a prime number? Yes, 7 is a prime number.
Is 9 a prime number? No, 9 is not a prime number. After all, 9 is divisible by itself, by one and by three.
Is 11 a prime number? Yes, 11 is a prime number.
Is 13 a prime number? Yes, 13 is a prime number.
Is 15 a prime number? No, 15 is not a prime number. After all, 15 is divisible by itself, by one, by three, by five.
Is 17 a prime number? Yes, 17 is a prime number.
Is 19 a prime number? Yes, 19 is a prime number.
Is 20 a prime number? No, 20 is not a prime number. After all, 20 is divisible by itself, by one, by two, by four, by five, by ten.
Is 777 a prime number? No, 777 is not a prime number. After all, 777 is divisible by itself, by one, by 3, by 7, by 37.
Is 997 a prime number? Yes, 997 is a prime number.
A prime number is a natural number that is divisible only by itself and one.