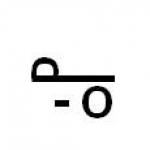The concept of % (share) of something
History of percentages, calculation of percentages, typing rules, colloquial use, problems involving percentages
Percentage is the definition
Concept percent
History of origin percent
Using percentages in everyday life
Types of Percentage Problems
Interest calculations
Percentages in programming
Percentage is the definition
percent- this is one hundredth. Indicated by the "%" sign. Used to indicate the proportion of something in relation to the whole. For example, 17% of 500 kg means 17 parts of 5 kg each, that is, 85 kg. This mathematical concept is often found in everyday life. The etymology of the term has Latin roots. The word "percent" comes from the Latin word pro centum, which literally translates to "per hundred" or "per hundred."


As an economic concept in the meaning of " "," benefit", "advantage" the word began to be used in the second half of the 19th century.
The financial definition of interest is a fee that one person () transfers to another person ( to the borrower) for the fact that the latter provides the former with funds for temporary use.
In modern financial vocabulary, interest is defined as a fee for the use of borrowed funds, such as rental income. When financiers talk about interest, they mean maturity, that is, such a rate in the discount rate that equals the discounted (reduced) price future results with its present price.
Business vocabulary - to work for interest means to work for remuneration calculated depending on arrived or turnover. In this regard, the percentage acts as a commission, which characterizes, first of all, the work of the broker

Interest concept
In the text, the percent sign is used only for numbers in digital form, from which, when typed, they are separated by a non-breaking space (67%), except in cases where the percent sign is used to abbreviate compound words formed using the numeral and the adjective "percentage"
percentage in Chinese is denoted by different words depending on whether it is used in a mathematical or economic sense. In its pure form, "percentage" is 百分比 (baifenbi), which literally translates as "a ratio of a hundred parts." So, for example, 10% will sound like “ten hundredths”. That is, in the Chinese percentage there is always a mention of “hundred” and there are no extraneous borrowed or ancient words, but only pure mathematics.
In the economic sense, interest is "profit." The word 利率 (lilyu) is used accordingly. The first hieroglyph is “profit”, the second is “coefficient”, that is, “profit coefficient”. The word itself can be translated as "interest, percentage (to capital), rate of return."

Percentage expressions in China are often used in expressions such as “over the past year, the country began to generate 9% more electricity.” Moreover, both the percentage sign “%” and the literal writing of the expression “nine hundredths” can be used.

0,07 % = 0,0007;
The rule for writing numbers and percentage signs separately was introduced in 1982 by the regulatory document GOST 8.417-81 (later replaced by GOST 8.417-2002); Previously, the norm was not to separate the percent sign with a space from the preceding digit.
Currently, the rule for removing the percent sign is not generally accepted. Until now, many Russian publishing houses do not follow the recommendations of GOST 8.417-2002 and still adhere to traditional typing rules, that is, when typing, the percent sign is not separated from the previous number.


Sometimes it is convenient to compare two values not by the difference in their values, but as a percentage. For example, price compare two products not in rubles, but evaluate how much more or less one product is than the price of another as a percentage. If comparison by difference is completely unambiguous, that is, you can always find how much one value is greater or less than another, then to compare as a percentage you need to indicate in relation to what value the percentage is calculated. Such an indication, however, is not necessary in the case where one value is said to be greater than another by a percentage greater than 100. In this case, there remains only one possibility for calculating the percentage, namely, dividing the difference by the smaller of the two numbers and then multiplying the result by 100.
Interest in economics
interest is the part of the profit that creditor pays the borrower for the money capital borrowed, and is defined as the “irrational form of price” of the loan capital. The source of interest is the surplus value created in the process of productive use of loan money. capital. The division of profit received from the use of loan capital into the percentage assigned by the loan capital and the profit itself - business income received by the lender, occurs under the influence of supply and demand in the loan capital market. Thus, interest expresses the relationship between the borrower and the lender and appears in the form of a certain interest rate.
Loan interest is the definition
Loan interest is a fee for the temporary use of the loaned value. This is an economic category that operates on the basis of credit relations. It expresses the relationship between borrower and borrower, who have their own specific interests in receiving and paying interest.
Unlike a loan, loan interest does not imply a repayable, but an irrevocable distribution of the value of the product produced. goods, and not the entire value, but only the value of surplus goods in its transformed form - profit. Interest is a direct deduction from the profit remaining at the disposal of the borrower. The amount of interest depends on the level of the interest rate and the amount loans received by the creditor.
The formation of a commercial bank’s lending policy should be based on taking into account the following most important factors:
Availability of capital;
The degree of riskiness and profitability of various types loans;
Stability of deposits;
General state of the economy states;
Impact on the economy of monetary and financial politicians;
Abilities and experience of banking personnel;
Loan needs of the district (region) served bank.
These factors undoubtedly influence the ongoing bank lending interest policy.
Modern state with a market economy, by controlling the movement of loan interest, it can influence almost all parameters of social production. In particular, by raising the loan interest rate, through the Central Bank it can contribute to monetary savings, lower prices and stabilization of wages, increased production efficiency and the growth of the national currency, reduced competitiveness of its goods, increased prices for exports and cheaper imports of goods, increased import capital and its containment exporting etc.
Deposit interest is the definition
Deposit interest is a fee paid by banks (credit institutions) for storing funds, securities and other material assets in accounts, depositories, and storage facilities. It expresses the relationship between two participants in a credit transaction, and its content has two sides. The borrowers in a deposit operation are the clients of the bank (credit institution) - enterprises, organizations, institutions, other banks, the population, and the borrower (borrower) is the (credit institution).
Level up interest rates on deposits (deposits) has not only economic significance, but also social significance. In conditions of inflation, it is difficult to ensure the protection of the interests of depositors, and therefore, they are not interested in placing funds for long-term storage. Therefore, the deposit interest policy of banks should be linked to comprehensive customer service.
Interest rates on deposits in some countries depend on the amount of deposits: as they increase, the income on the deposit increases. In order to stimulate savings, especially for a long period, credit institutions in foreign countries pay depositors quite high interest rates (with taking into account low inflation), in particular, in the USA - from 5.7 to 9.8%, in Britain - from 3.0 to 11.2%, in Germany - from 2.5 to 5.2%, in France - from 4, 5 to 7.5%, in Italy - from 5.0 to 12.3%.
Interest calculation methods
In banking practice, there are various methods and methods for calculating interest.
Simple and compound interest applies.
Simple interest is the definition
Simple interest is accrual method, in which the amount of interest is determined throughout the entire period, based on the original amount of debt, regardless of the amount periods accruals and their duration.
Simple interest is when interest on the deposit is calculated at the end deadline. For example, open contribution for a year, with interest paid at the end of the deposit term.
The formula for calculating simple interest is:
Compound interest - definition
Compound interest is a method of calculating interest in which accruals occur on the initial amount of the deposit (debt) and on the increase in the deposit (debt), i.e. the amount of interest accrued after the first accrual period. Thus, the basis for calculating compound interest (as opposed to simple interest) will increase with each accrual period.
The compound interest formula looks like this:
interest rate is the definition
the interest rate is determined in accordance with the specific conditions for the use of loan capital and is the object of monetary and credit regulation by central bank. At the same time, the value of interest rates contributes either to the inflow of monetary capital from the money markets of other countries, or to its outflow.
Commercial banks set interest rates based on the discount rates adopted by the central banks of their countries. In this case, large banks determine the minimum or best rates on loans provided to prime borrowers.
Interest on deposits of bank clients is important in the structure of interest rates. The interest paid by banks to their clients is always significantly lower than the interest on loans (due to this difference, one of the main sources of banking profit is formed - interest margin)
Interest margin- this is the definition
Used to replace non-ASCII characters in URI strings as codes like %D0%9F%D1%80%D0%BE (percent sign first, followed by two-digit hexadecimal number).
In SQL, the percent sign with the LIKE command replaces any number of any characters, that is, it provides a search by mask.
In Matlab programs, LaTeX markup and PostScript, the percent sign is used before the beginning of a line text comment.
Calculators have a percentage button. Depending on the organizations Manufacturer's simplest calculators calculate.
One of the basic concepts of mathematics is percentage. In order to understand what a percentage is, it is enough to divide the given whole value by one hundred. One hundredth would be one percent (denoted 1%). Both in the exact and economic sciences, and in other areas of life, percentages are used to indicate shares in relation to the whole. In this case, the whole itself is designated as 100%. In some cases, it is used when comparing two values: for example, sometimes the cost of goods is not compared in monetary units, but is estimated by how many% the price of one product is more or less than the price of another. The term has also become widespread in banking and is mostly used as a synonym for interest rate.
Rule for finding percentages of a number
Calculating percentages of a whole is one of the basic mathematical operations, and is also often used in everyday life. The rule for finding percentages of a number states that to solve such a problem, it must be multiplied by the amount of % specified in the conditions, after which the resulting result is divided by 100. You can also divide the number by 100, and the resulting result is multiplied by the specified amount of %. It is important to remember one more thesis: if the percentage specified by the conditions exceeds 100%, then the resulting numerical value is always greater than the initial (specified) one - and vice versa.
The rule for finding a number by its percentage
There is an inverse rule for finding a number by its percentage. In order to obtain the result of such a mathematical operation (the second of the three basic types of problems for percentage calculations), it is necessary to divide the number specified in the conditions by a given percentage value, after which the resulting result is multiplied by 100. In this case, the first action is to calculate the number of units of the original value in 1 %, and the second - in general (that is, 100%). If the number of % exceeds 100, then the result obtained will always be less than the numerical value specified by the conditions of the problem - and vice versa.
The rule for finding the percentage expression of a number from another
The third basic type of mathematical problems involving percentage calculations are those in which it is necessary to use the rule for finding the percentage expression of a number from another (or the ratio of two quantities). It says that to solve it is necessary to divide the second number by the first, after which the resulting result is multiplied by one hundred. Such a ratio shows how many % one numerical value is from another (that is, in fact we are talking about the relationship between two numerical values, expressed in %).
Calculating interest is a simple mathematical operation that is quite common in everyday life. For example, you need to calculate how much a person saves by using a store discount card or buying an item on sale at a discount, and at what percentage the loan is taken out. Percentages can be calculated using a calculator or proportion; a formula for calculating percentages and knowledge of basic known ratios will be useful.
What is a percentage of a number
Calculating percentages in the school curriculum is studied in the 5th grade, if not earlier. By definition, a percentage is one hundredth of a number. The term originated in Ancient Rome and literally translates as “from a hundred.” The idea of calculating percentages originally originated in Babylon. At the same time, in Ancient India they learned to calculate percentages using proportions.
In order to find the percentage of a number, you need to divide the number by 100. Obviously, 1% of 100 equals one.
Calculating interest using formulas
The formula to find the percentage of a number is simple. You need to divide the number by 100, then multiply by the desired percentage.
If we take the original number as X, and the desired percentage as Y, then the formula is written as X/100*Y=...

Calculations using proportions
Calculating percentages can be done with an understanding of the proportion method. Let A be the main number taken as 100%, B the number whose relationship with A as a percentage must be calculated, and X the number of the desired percentages. Then:
A - 100%,
B - X%.
Multiplying crosswise will give the equality: A*X=B*100. Therefore, X=B*100/A.
For example, you need to find out what percentage of 300 is the number 75. It turns out: 75*100/300=25%.
Alternative calculation method
Let's represent one percent not as a decimal, but as a simple fraction - 1/100. Similarly, you can write any number of percentages. So, 10% is 0.1 or 1/10, 25% is 0.25 or 25/100=1/4 and so on. Therefore, finding 10% of a number is quite simple - you need to divide the original number by 10. In this way it is convenient to calculate 20, 25 and 50 percent:
- 20% is 1/5, which means you need to divide the original number by 5.
- 25% is 1/4, you need to divide by 4.
- 50% is 1/2, just divide by two.
But not every percentage is convenient to calculate using this method. For example, 33% is 33/100, which when written as a decimal gives 0.3333 with an infinite number of threes after the decimal point.
If you have any doubts about the correctness of your calculations, you can always check yourself using a calculator, which is now available on any mobile device and on any computer.
Percentages in mathematics. Problems involving percentages.
Attention!
There are additional
materials in Special Section 555.
For those who are very "not very..."
And for those who “very much…”)
Percentages in mathematics.
What's happened percentages in mathematics? How to decide percent problems? These questions pop up, alas, suddenly... When a graduate reads the Unified State Exam assignment. And they put him at a dead end. But in vain. These are very simple concepts.
The only thing you need to remember is what it is one percent . This concept is master key to solving problems involving percentages, and to working with percentages in general.
One percent is one hundredth of a number . That's all. There is no more wisdom.
A reasonable question - what about the hundredth part? what date ? But the number that is discussed in the task. If it talks about price, one percent is one hundredth of the price. If we talk about speed, one percent is one hundredth of the speed. And so on. It is clear that the number itself in question is always 100%. And if there is no number itself, then percentages have no meaning...
Another thing is that in complex problems the number itself will be hidden so much that you won’t find it. But we are not aiming at the complicated yet. Let's deal with percentages in mathematics.
It’s not for nothing that I emphasize words one percent, one hundredth. Remembering what it is one percent, you can easily find two percent, and thirty-four, and seventeen, and one hundred and twenty-six! You will find as much as you need.
And this, by the way, is the main skill for solving problems involving percentages.
Shall we try?
Let's find 3% of 400. First let's find one percent. This will be one hundredth, i.e. 400/100 = 4. One percent is 4. How much percent do we need? Three. So we multiply 4 by three. We get 12. That's it. Three percent of 400 is 12.
5% of 20 is 20 divided by 100 (one hundredth is 1%) and multiplied by five (5%):
5% of 20 will be 1. That's it.
It couldn't be simpler. Let's quickly practice before we forget!
Find how much it will be:
5% from 200 rubles.
8% of 350 kilometers.
120% from 10 liters.
15% of 60 degrees.
4% of excellent students out of 25 students.
10% of poor students out of 20 people.
Answers (in complete disorder): 9, 10, 2, 1, 28, 12.
These numbers are the number of rubles, degrees, students, etc. I didn’t write how much of what, so that it would be more interesting to decide...
What if we need to write down X% from some number, for example, from 50? Yes, everything is the same. One percent of 50 – how much? That's right, 50/100 = 0.5. And we have this percentage - X. Well, let's multiply 0.5 by X! We get that X% from 50 this is – 0.5x.
I hope so percentages in mathematics you got it. And you can easily find any percentage of any number. It's simple. You can now handle approximately 60% of all percentage problems! Already more than half. Well, let's finish off the rest? Okay, whatever you say!
In problems involving percentages, the opposite situation often occurs. They give us quantities (any kind), but we need to find interest . Let's master this simple process.
3 people out of 120 – what percentage? Do not know? Well then, let it be X percent.
Let's calculate X% from 120 people. In people. This is what we can do. Divide 120 by 100 (calculate 1%) and multiply by X(we calculate X%). We get 1.2 X.
Let's understand the result.
X percent from 120 people, this is 1.2 X Human . And we have three such people. It remains to equate:

We remember that for X we took the number of percents. This means 3 people out of 120 people is 2.5%.
That's all.
It can be done differently. You can do it with simple ingenuity, without any equations. Let's think , how many times 3 people less than 120? Divide 120 by 3 and get 40. This means that 3 is 40 times less than 120.
The required number of people in percentage will be the same amount of times less than 100%. After all, 120 people is 100%. Divide 100 by 40, 100/40 = 2.5
That's all. We received 2.5%.
There is also a method of proportions, but this is essentially the same thing in an abbreviated version. All these methods are correct. Whatever is more convenient, familiar, and understandable to you – consider it that way.
We're training again.
Calculate the percentage:
3 people out of 12.
10 rubles from 800.
4 textbooks out of 160 books.
24 correct answers to 32 questions.
2 guessed answers to 32 questions.
9 hits out of 10 shots.
Answers (in order): 75%, 25%, 90%, 1.25%, 2.5%, 6.25%.
In the process of calculations, you may well encounter fractions. Including inconvenient ones, like 1.333333... Who told you to use a calculator? Yourself? No need. Count without a calculator , as written in the topic “Fractions”. There are all sorts of percentages...
So we have mastered the transition from quantities to percentages and back. You can take on tasks.
Problems involving percentages.
Problems involving percentages are very popular in the Unified State Examination. From the simplest to the most complex. In this section we work with simple tasks. In simple problems, as a rule, you need to move from percentages to the quantities discussed in the problem. To rubles, kilograms, seconds, meters, and so on. Or vice versa. We already know how to do this. After this, the problem becomes clear and easy to solve. Don't believe me? See for yourself.
Let us have such a problem.
“A bus ride costs 14 rubles. During school holidays, a 25% discount was introduced for students. How much does it cost to travel by bus during school holidays?
How to decide? If we find out how much 25% in rubles– then there’s nothing to decide. Let's subtract the discount from the original price - and that's it!
But we already know how to recognize this! How much will one percent from 14 rubles? One hundredth part. That is, 14/100 = 0.14 rubles. And we have 25 such percentages. So let’s multiply 0.14 rubles by 25. We get 3.5 rubles. That's all. We have established the discount amount in rubles, all that remains is to find out the new fare:
14 – 3,5 = 10,5.
Ten and a half rubles. This is the answer.
As soon as we switched from interest to rubles, everything became simple and clear. This is a general approach to solving percentage problems.
It is clear that not all tasks are equally elementary. There are more complicated ones. Just think! We will solve them now too. The difficulty is that it's the other way around. We are given some quantities, but we need to find the percentages. For example, this task:
“Previously, Vasya solved two problems out of twenty correctly. After studying the topic on one useful website, Vasya began to solve 16 out of 20 problems correctly. By what percentage did Vasya become wiser? We consider 20 solved problems to be 100% smart.”
Since the question is about percentages (and not rubles, kilograms, seconds, etc.), then we move on to percentages. Let's find out what percentage Vasya solved before understanding, what percentage after – and it’s in the bag!
We count. Two problems out of 20 – what percentage? 2 is 10 times less than 20, right? This means the number of problems in percentages will be 10 times less than 100%. That is, 100/10 = 10.
10%. Yes, Vasya decided a little... There is nothing to do at the Unified State Exam. But now he has become wiser, and solves 16 problems out of 20. Let’s calculate what percentage this will be? How many times is 16 less than 20? You can’t tell offhand... You’ll have to divide it.
5/4 times. Well, now we divide 100 by 5/4:

Here. 80% is already solid. And most importantly – the sky’s the limit!
But this is not the answer yet! We read the problem again so as not to make a mistake out of the blue. Yes, they ask us for how long Has Vasya become a percent wiser? Well, it's simple. 80% - 10% = 70%. By 70%.
70% is the correct answer.
As you can see, in simple problems it is enough to convert given values into percentages, or given percentages into values, and everything becomes clearer. It is clear that the problem may well contain additional bells and whistles. Which, often, have nothing to do with percentages at all. Here, the main thing is to read the condition carefully and, step by step, slowly, unfold the problem. We will talk about this in the next topic.
But there is one serious ambush in problems involving percentages! Many people fall into it, yes... This ambush looks quite innocent. For example, here’s a problem.
“A beautiful notebook cost 40 rubles in the summer. Before the start of the school year, the seller raised the price by 25%. However, notebooks began to sell so poorly that he reduced the price by 10%. They still don't take it! He had to reduce the price by another 15%. This is where the trade started! What was the final price of the notebook?”
Well, how? Elementary?
If you quickly and joyfully answered “40 rubles!”, then you were ambushed...
The trick is that interest is always calculated from something .
So we count. How long rubles did the seller inflate the price? 25% from 40 rubles - that's 10 rubles. That is, the notebook, which has become more expensive, now costs 50 rubles. This is understandable, right?
And now we need to reduce the price by 10% from 50 rubles. From 50, not 40! 10% of 50 rubles is 5 rubles. Consequently, after the first reduction in price, the notebook began to cost 45 rubles.
We consider the second reduction in price. 15% from 45 rubles ( from 45, not 40, or 50! ) is 6.75 rubles. Therefore, the final price of the notebook is:
45 – 6.75 = 38.25 rubles.
As you can see, the catch is that the interest is calculated each time from the new price. From the last one. This happens almost always. If in the problem of sequential increase-decrease of a value it is not stated in plain text, from what To count percentages, you need to count them from the last value. And that's true. How does the seller know how many times this notebook has gone up and down in price before him and how much it cost at the very beginning...
By the way, now you may be thinking, why is the last phrase written in the problem about smart Vasya? This one: " Do we consider 20 solved problems to be 100% smart? It seems that everything is clear... Uh-uh... How to say. If this phrase is not there, Vasya may well count his initial successes as 100%. That is, two solved problems. And 16 tasks are eight times more. Those. 800%! Vasya will be able to justifiably talk about his own wisdom by as much as 700%!
You can also take 16 tasks for 100%. And get a new answer. Also correct...
Hence the conclusion: The most important thing in problems involving percentages is to clearly determine from what one or another percentage should be calculated.
By the way, this is necessary in life too. Where percentages are used. In stores, banks, at all sorts of promotions. Otherwise you expect a 70% discount, but you get 7%. And not discounts, but increases in prices... And everything is fair, I miscalculated myself.
Well, you got the idea of percentages in mathematics. Let's note the most important thing.
Practical tips:
1. In problems involving percentages, we move from percentages to specific quantities. Or, if necessary, from specific values to percentages. Read the task carefully!
2. We study very carefully, from what interest must be calculated. If this is not stated directly, it is necessarily implied. When changing a value sequentially, percentages are assumed from the last value. Read the task carefully!
3. Having finished solving the problem, read it again. It is quite possible that you have found an intermediate answer, not a final one. Read the task carefully!
Solve several problems involving percentages. To consolidate, so to speak. In these puzzles I tried to collect all the main difficulties that await the solvers. Those rake that are most often stepped on. Here they are:
1. Elementary logic in the analysis of simple problems.
2. Correct choice of value from which to calculate percentages. How many people have stumbled on this! But there is a very simple rule...
3. Interest on interest. It's a small thing, but it's really annoying...
4. And another pitchfork. Relationship between percentages and fractions and parts. Translating them into each other.
“50 people took part in the mathematics Olympiad. 68% of students solved few problems. 75% of the remaining solved moderate problems, and the rest solved many problems. How many people have solved many problems?
Clue. If you get fractional students, this is wrong. Read the problem carefully, there is one important word there... Another problem:
“Vasya (yes, the same one!) really loves donuts with jam. Which are baked in a bakery, one stop from home. Donuts cost 15 rubles apiece. Having 43 rubles available, Vasya went to the bakery by bus for 13 rubles. And in the bakery there was a promotion “Discount on everything - 30%!!!”. Question: how many additional donuts was Vasya unable to buy because of his laziness (he could have gone for a walk, right?)”
Short problems.
What percent is 4 less than 5?
What percentage is 5 greater than 4?
Long task...
Kolya got a simple job involving calculating interest. During the interview, the boss with a sly smile offered Kolya two options for remuneration. According to the first option, Kolya was immediately assigned a rate of 15,000 rubles per month. According to the second Kolya, if he agrees, for the first 2 months he will pay a salary reduced by 50%. Kind of like a newbie. But then they will increase his reduced salary by as much as 80%!
Kolya visited a useful site on the Internet... Therefore, after thinking for six seconds, he chose the first option with a slight smile. The boss smiled back and set Kolya a permanent salary of 17,000 rubles.
Question: How much money per year (in thousands of rubles) did Kolya win at this interview? Compared to the worst option? And one more thing: why were they smiling all the time!?)
Another short problem.
Find 20% of 50%.
And again long.)
Fast train No. 205 "Krasnoyarsk - Anapa" made a stop at the "Syzran-Gorod" station. Vasily and Kirill went to the station store to get ice cream for Lena and a hamburger for themselves. When they bought everything they needed, the store cleaner said that their train had already left... Vasily and Kirill quickly ran and managed to jump into the carriage. Question: would the world champion runner have time to jump into the carriage under these conditions?
We believe that under normal conditions the world champion runs 30% faster than Vasily and Kirill. However, the desire to catch up with the carriage (it was the last one), treat Lena to ice cream and eat a hamburger, increased their speed by 20%. And ice cream with a hamburger in the hands of a champion and flip-flops on his feet would reduce his speed by 10%...
But here’s a problem without percentages... I wonder why it’s here?)
Determine how much 3/4 of an apple weighs if the entire apple weighs 200 grams?
And the last one.
On the fast train No. 205 "Krasnoyarsk - Anapa", fellow travelers were solving a crossword puzzle. Lena guessed 2/5 of all the words, and Vasily guessed one third of the remaining ones. Then Kirill joined in and solved 30% of the entire crossword puzzle! Seryozha guessed the last 5 words. How many words were there in the scanword? Is it true that Lena guessed the most words?
The answers are in the traditional disorder and without unit names. Where are the donuts, where are the students, where are the rubles with interest - that’s you...
10; 50; Yes; 4; 20; No; 54; 2; 25; 150.
So how is it? If everything comes together - congratulations! Interest is not your problem. You can safely go to work in a bank.)
Is there something wrong? Does not work? Don't know how to quickly calculate percentages of a number? Don’t know very simple and clear rules? From what to calculate interest, for example? Or, how to convert fractions to percentages?
If you like this site...
By the way, I have a couple more interesting sites for you.)
You can practice solving examples and find out your level. Testing with instant verification. Let's learn - with interest!)
You can get acquainted with functions and derivatives.
Perhaps math wasn't your favorite subject in school, and numbers were scary and boring. But in adult life there is no escape from them. Without calculations, you can’t fill out a receipt for paying for electricity, you can’t draw up a business project, you can’t help your child with his homework. Often in these and other cases it is necessary to calculate the percentage of the amount. How to do this if you have vague memories of what percentage is from your school days? Let's strain our memory and figure it out.
Method one: percentage of the amount by determining the value of one percent
A percentage is one hundredth of a number and is denoted by the % sign. If you divide the amount by 100, you get just one percent. And then everything is simple. We multiply the resulting number by the required percentage. In this way it is easy to calculate the profit on a bank deposit.
For example, you deposited an amount of 30,000 at 9% per annum. What will be the profit? We divide the amount of 30,000 by 100. We get the value of one percent - 300. Multiply 300 by 9 and get 2,700 rubles - an increase to the original amount. If the contribution is for two or three years, then this figure doubles or triples. There are deposits for which interest payments are made monthly. Then you need to divide 2700 by 12 months. 225 rubles will be a monthly profit. If interest is capitalized (added to the total account), then the deposit amount will increase every month. This means that the percentage will be calculated not from the down payment, but from the new indicator. Therefore, at the end of the year you will receive a profit of not 2,700 rubles, but more. How many? Try to count.
Method two: convert percentages to decimals
As you remember, a percentage is a hundredth of a number. As a decimal it is 0.01 (zero point one hundredth). Therefore, 17% is 0.17 (zero point, seventeen hundredths), 45% is 0.45 (zero point, forty-five hundredths), etc. We multiply the resulting decimal fraction by the amount of which we calculate the percentage. And we find the answer we are looking for.
For example, let's calculate the amount of income tax from a salary of 35,000 rubles. The tax is 13%. As a decimal it would be 0.13 (zero point one, thirteen hundredths). Let's multiply the amount of 35,000 by 0.13. It will turn out to be 4,550. This means that after deducting income tax, you will receive a salary of 35,000 - 4,550 = 30,050. Sometimes this amount, already without tax, is called “salary in hand” or “net.” In contrast, the amount together with tax is “dirty salary”. It is the “dirty salary” that is indicated in company vacancy announcements and in the employment contract. Less is given to your hands. How many? Now you can easily count.

Method three: count on a calculator
If you doubt your mathematical abilities, use a calculator. With its help, it is calculated faster and more accurately, especially when it comes to large amounts. It is easier to work with a calculator that has a button with a percentage sign. Multiply the amount by the percentage and press the % button. The required answer will be displayed on the screen.
For example, you want to calculate what your child care benefit will be for up to 1.5 years. It is 40% of average earnings for the last two closed calendar years. Let’s say the average salary is 30,000 rubles. On the calculator, multiply 30,000 by 40 and press the % button. Key = no need to touch. The answer 12,000 will be displayed on the screen. This will be the amount of the benefit.
As you can see, everything is very simple. Moreover, the “Calculator” application is now available on every cell phone. If the device does not have a special % button, then use one of the two methods described above. And perform multiplication and division on a calculator, which will facilitate and speed up your calculations.
Don't forget: there are online calculators to make calculations easier. They operate in the same way as regular ones, but are always at hand when you work on the computer.

Method four: making a proportion
You can calculate the percentage of the amount using a proportion. This is another scary word from a school mathematics course. Proportion is equality between two ratios of four quantities. For clarity, it is better to immediately understand it with a specific example. You want to buy boots for 8,000 rubles. The price tag indicates that they are sold at a 25% discount. How much is this in rubles? Of the 4 values, we know 3. There is a sum of 8,000, which is equal to 100%, and 25% that needs to be calculated. In mathematics, an unknown quantity is usually called X. The proportion we get is:
For ease of calculation, we convert percentages to decimal fractions. We get:
The proportion is solved as follows: X = 8,000 * 0.25: 1X = 2,000
2,000 rubles – discount on boots. We subtract this amount from the old price. 8,000 – 2,000= 6,000 rubles (new discounted price). This is such a nice proportion.

This method can also be used to determine the value of 100%, if you know the numerical indicator - say, 70%. At a company-wide meeting, the boss announced that 46,900 units of goods had been sold during the year, while the plan was only 70% fulfilled. How much did you need to sell to fully fulfill the plan? Let's make a proportion:
Converting percentages to decimal fractions, it turns out:
Let’s solve the proportion: X = 46,900 * 1: 0.7X = 67,000. These were the results of the work that the bosses expected.
As you may have guessed, the proportion method can be used to calculate what percentage a numerical indicator is of the amount. For example, while taking a test, you answered 132 out of 150 questions correctly. What percent of the task was completed?
There is no need to convert this proportion into decimal fractions; you can solve it right away.
X = 100 * 132: 150. As a result, X = 88%
As you can see, it's not all that scary. A little patience and attention, and now you have mastered the calculation of percentages.