Detaljno se razmatraju primjeri rješenja integrala po dijelovima čiji je integrand umnožak polinoma s eksponencijalom (e na x potenciju) ili sinusom (sin x) ili kosinusom (cos x).
SadržajVidi također: Metoda integracije po dijelovima
Tablica neodređenih integrala
Metode izračunavanja neodređenih integrala
Osnovne elementarne funkcije i njihova svojstva
Formula za integraciju po dijelovima
Pri rješavanju primjera u ovom odjeljku koristi se formula integracije po dijelovima:
;
.
Primjeri integrala koji sadrže umnožak polinoma i sin x, cos x ili e x
Evo primjera takvih integrala:
, , .
Za integraciju takvih integrala, polinom se označava s u, a preostali dio s v dx. Zatim primijenite formulu integracije po dijelovima.
Ispod je detaljno rješenje ovih primjera.
Primjeri rješavanja integrala
Primjer s eksponentom, e na potenciju x
Odredite integral:
.
Uvedimo eksponent ispod predznaka diferencijala:
e - x dx = - e - x d(-x) = - d(e - x).
Integrirajmo po dijelovima.
Ovdje
.
Preostali integral također integriramo po dijelovima.
.
.
.
Konačno imamo:
.
Primjer definiranja integrala sa sinusom
Izračunajte integral:
.
Uvedimo sinus ispod diferencijalnog znaka:
Integrirajmo po dijelovima.
ovdje je u = x 2 , v = cos(2 x+3), du = (
x 2 )′
dx
Preostali integral također integriramo po dijelovima. Da biste to učinili, uvedite kosinus ispod diferencijalnog znaka.
ovdje u = x, v = grijeh(2 x+3), du = dx
Konačno imamo:
Primjer umnoška polinoma i kosinusa
Izračunajte integral:
.
Uvedimo kosinus ispod diferencijalnog predznaka:
Integrirajmo po dijelovima.
ovdje je u = x 2 + 3 x + 5, v = grijeh 2 x, du = (
x 2 + 3 x + 5 )′
dx
Kompleksni integrali
Ovaj članak zaključuje temu neodređenih integrala i uključuje integrale koje smatram prilično složenima. Lekcija je nastala na višestruke zahtjeve posjetitelja koji su izrazili želju da se teži primjeri analiziraju na stranici.
Pretpostavlja se da je čitatelj ovog teksta dobro pripremljen i da zna primijeniti osnovne tehnike integracije. Lutke i ljudi koji nisu baš sigurni u integrale neka pogledaju već prvu lekciju - Neodređeni integral. Primjeri rješenja, gdje možete svladati temu gotovo od nule. Iskusniji studenti mogu se upoznati s tehnikama i metodama integracije koje do sada nisu susrele u mojim člancima.
Koji će se integrali razmatrati?
Prvo ćemo razmotriti integrale s korijenima, za čije rješavanje sukcesivno koristimo zamjena varijable I integracija po dijelovima. To jest, u jednom primjeru dvije tehnike se kombiniraju odjednom. I još više.
Zatim ćemo se upoznati sa zanimljivim i originalnim metoda svođenja integrala na sebe. Dosta integrala se rješava na ovaj način.
Treće izdanje programa bit će integrali složenih razlomaka, koji su prošli pored blagajne u prethodnim člancima.
Četvrto, analizirat će se dodatni integrali iz trigonometrijskih funkcija. Konkretno, postoje metode koje izbjegavaju dugotrajnu univerzalnu trigonometrijsku zamjenu.
(2) U funkciji integranda dijelimo brojnik s nazivnikom član po član.
(3) Koristimo svojstvo linearnosti neodređenog integrala. U posljednjem integralu odmah staviti funkciju pod predznak diferencijala.
(4) Uzimamo preostale integrale. Imajte na umu da u logaritmu možete koristiti zagrade umjesto modula, jer .
(5) Vršimo obrnutu zamjenu, izražavajući "te" iz izravne zamjene:
Mazohistički studenti mogu diferencirati odgovor i dobiti izvorni integrand, kao što sam ja upravo učinio. Ne, ne, provjerio sam u pravom smislu =)
Kao što možete vidjeti, tijekom rješavanja smo morali koristiti čak i više od dvije metode rješavanja, tako da su vam za rad s takvim integralima potrebne pouzdane vještine integracije i prilično malo iskustva.
U praksi je, naravno, kvadratni korijen češći, evo tri primjera za samostalno rješavanje:
Primjer 2
Nađi neodređeni integral
Primjer 3
Nađi neodređeni integral
Primjer 4
Nađi neodređeni integral
Ovi primjeri su iste vrste, tako da će kompletno rješenje na kraju članka biti samo za primjer 2; primjeri 3-4 imaju iste odgovore. Koju zamjenu koristiti na početku odluka, mislim da je očito. Zašto sam odabrao primjere iste vrste? Često se nalaze u njihovoj ulozi. Češće, možda, samo nešto slično ![]() .
.
Ali ne uvijek, kada ispod arktangensa, sinusa, kosinusa, eksponencijala i drugih funkcija postoji korijen linearne funkcije, morate koristiti nekoliko metoda odjednom. U nizu slučajeva moguće je "lako se riješiti", odnosno odmah nakon zamjene dobije se jednostavan integral koji se lako može uzeti. Najlakši od gore predloženih zadataka je primjer 4, u kojem se nakon zamjene dobiva relativno jednostavan integral.
Svođenjem integrala na sebe
Duhovita i lijepa metoda. Pogledajmo klasike žanra:
Primjer 5
Nađi neodređeni integral
Pod korijenom je kvadratni binom, a pokušaj integracije ovog primjera može čajniku zadati glavobolju satima. Takav se integral uzima u dijelovima i svodi na sebe. U principu, nije teško. Ako znate kako.
Označimo integral koji razmatramo latiničnim slovom i započnemo rješenje: ![]()
Integrirajmo po dijelovima: 

(1) Pripremite funkciju integranda za dijeljenje član po član.
(2) Funkciju integranda dijelimo član po član. Možda neće svima biti jasno, ali opisat ću to detaljnije:
(3) Koristimo svojstvo linearnosti neodređenog integrala.
(4) Uzmite posljednji integral (“dugi” logaritam).
Sada pogledajmo sam početak rješenja: 
I na kraju: 
Što se dogodilo? Kao rezultat naših manipulacija, integral je reduciran na sebe!
Izjednačimo početak i kraj: ![]()
Pomaknite se na lijevu stranu s promjenom predznaka: ![]()
I pomaknemo dva na desnu stranu. Kao rezultat: ![]()
Konstantu je, strogo govoreći, trebalo dodati ranije, ali ja sam je dodao na kraju. Toplo preporučujem da pročitate o čemu se radi ovdje:
Bilješka:
Strože, završna faza rješenja izgleda ovako:
Tako:
Konstanta se može ponovno označiti s . Zašto se može prenamijeniti? Jer on to još uvijek prihvaća bilo koji vrijednosti, te u tom smislu nema razlike između konstanti i.
Kao rezultat:
Sličan trik sa stalnim renotacijama naširoko se koristi u diferencijalne jednadžbe. I tu ću biti strog. I ovdje dopuštam takvu slobodu samo kako vas ne bi zbunio nepotrebnim stvarima i kako bih pozornost usmjerio upravo na sam način integracije.
Primjer 6
Nađi neodređeni integral
Još jedan tipičan integral za neovisno rješenje. Potpuno rješenje i odgovor na kraju lekcije. Bit će razlika s odgovorom u prethodnom primjeru!
Ako se ispod kvadratnog korijena nalazi kvadratni trinom, tada se rješenje u svakom slučaju svodi na dva analizirana primjera.
Na primjer, razmotrite integral ![]() . Sve što trebate učiniti je prvo odaberite cijeli kvadrat:
. Sve što trebate učiniti je prvo odaberite cijeli kvadrat:
.
Zatim se provodi linearna zamjena, koja radi "bez ikakvih posljedica":
, što rezultira integralom . Nešto poznato, zar ne?
Ili ovaj primjer, s kvadratnim binomom:
Odaberite cijeli kvadrat:
I, nakon linearne zamjene, dobivamo integral, koji se također rješava pomoću algoritma o kojem smo već govorili.
Pogledajmo još dva tipična primjera redukcije integrala na sebe:
– integral eksponencijala pomnoženog sa sinusom;
– integral eksponencijala pomnoženog s kosinusom.
U navedene integrale po dijelovima morat ćete integrirati dva puta:
Primjer 7
Nađi neodređeni integral
Integrand je eksponencijal pomnožen sa sinusom.
Dvaput integriramo po dijelovima i reduciramo integral na sebe: ![]()



Kao rezultat dvostruke integracije po dijelovima, integral se reducirao na sebe. Izjednačavamo početak i kraj rješenja:
Pomaknemo ga na lijevu stranu s promjenom predznaka i izrazimo svoj integral: 
Spreman. Istodobno, preporučljivo je češljati desnu stranu, tj. izvadite eksponent iz zagrada, a sinus i kosinus stavite u zagrade "lijepim" redom.
Vratimo se sad na početak primjera, točnije na integraciju po dijelovima: ![]()
Eksponent smo označili kao. Postavlja se pitanje: treba li eksponent uvijek označavati s ? Nije potrebno. Zapravo, u razmatranom integralu temeljno nema veze, što mislimo pod , mogli smo ići drugim putem: 
Zašto je to moguće? Budući da se eksponencijal pretvara u sebe (i tijekom diferencijacije i integracije), sinus i kosinus se međusobno pretvaraju (opet, i tijekom diferencijacije i integracije).
Odnosno, možemo također označiti trigonometrijsku funkciju. Ali u razmatranom primjeru to je manje racionalno, jer će se pojaviti razlomci. Ako želite, možete pokušati riješiti ovaj primjer koristeći drugu metodu; odgovori se moraju podudarati.
Primjer 8
Nađi neodređeni integral
Ovo je primjer koji trebate sami riješiti. Prije nego se odlučite, razmislite što je u ovom slučaju korisnije označiti kao , eksponencijalnu ili trigonometrijsku funkciju? Potpuno rješenje i odgovor na kraju lekcije.
I, naravno, ne zaboravite da je većinu odgovora u ovoj lekciji prilično lako provjeriti diferencijacijom!
Razmotreni primjeri nisu bili najsloženiji. U praksi su češći integrali gdje je konstanta i u eksponentu iu argumentu trigonometrijske funkcije, na primjer: . Mnogi će se zbuniti u takvom integralu, a i sam se često zbunim. Činjenica je da postoji velika vjerojatnost da će se razlomci pojaviti u otopini, a vrlo je lako izgubiti nešto nepažnjom. Osim toga, postoji velika vjerojatnost pogreške u predznacima; imajte na umu da eksponent ima predznak minus, a to predstavlja dodatnu poteškoću.
U završnoj fazi rezultat je često ovako:
Čak i na kraju rješenja, trebali biste biti izuzetno oprezni i ispravno razumjeti razlomke: 
Integriranje složenih razlomaka
Polako se približavamo ekvatoru lekcije i počinjemo razmatrati integrale razlomaka. Opet, nisu svi supersloženi, samo su iz ovog ili onog razloga primjeri malo "izvan teme" u drugim člancima.
Nastavljajući temu korijena
Primjer 9
Nađi neodređeni integral
U nazivniku ispod korijena nalazi se kvadratni trinom plus "pridatak" u obliku "X" izvan korijena. Integral ovog tipa može se riješiti standardnom zamjenom.
Mi odlučujemo: ![]()
Zamjena je ovdje jednostavna: ![]()
Pogledajmo život nakon zamjene: 
(1) Nakon supstitucije članove pod korijenom svodimo na zajednički nazivnik.
(2) Vadimo ga ispod korijena.
(3) Brojnik i nazivnik smanjeni su za . U isto vrijeme, ispod korijena, preuredio sam pojmove u prikladnom redoslijedu. Uz određeno iskustvo, korake (1), (2) možete preskočiti izvođenjem komentiranih radnji usmeno.
(4) Rezultirajući integral, kao što se sjećate iz lekcije Integriranje nekih razlomaka, odlučuje se metoda potpune kvadratne ekstrakcije. Odaberite cijeli kvadrat.
(5) Integracijom dobivamo obični “dugi” logaritam.
(6) Vršimo obrnutu zamjenu. Ako u početku , zatim natrag: .
(7) Završna radnja je usmjerena na izravnavanje rezultata: ispod korijena ponovo dovodimo pojmove na zajednički nazivnik i vadimo ih ispod korijena.
Primjer 10
Nađi neodređeni integral ![]()
Ovo je primjer koji trebate sami riješiti. Ovdje se samom "X" dodaje konstanta, a zamjena je gotovo ista: ![]()
Jedino što dodatno trebate učiniti je izraziti “x” iz zamjene koja se provodi: ![]()
Potpuno rješenje i odgovor na kraju lekcije.
Ponekad u takvom integralu ispod korijena može biti kvadratni binom, to ne mijenja metodu rješenja, bit će još jednostavnija. Osjeti razliku:
Primjer 11
Nađi neodređeni integral
Primjer 12
Nađi neodređeni integral
Kratka rješenja i odgovori na kraju lekcije. Treba napomenuti da je primjer 11 upravo binomni integral, o čijoj se metodi rješavanja raspravljalo u razredu Integrali iracionalnih funkcija.
Integral nerastavljivog polinoma 2. stupnja na potenciju
(polinom u nazivniku)
Rjeđi tip integrala, ali se ipak susreće u praktičnim primjerima.
Primjer 13
Nađi neodređeni integral
Ali vratimo se primjeru sa sretnim brojem 13 (iskreno, nisam dobro pogodio). Ovaj integral je također jedan od onih koji mogu biti prilično frustrirajući ako ne znate kako riješiti.
Rješenje počinje umjetnom transformacijom: 
Mislim da je svima već jasno kako podijeliti brojnik nazivnikom pojam po pojam.
Rezultirajući integral uzima se u dijelovima: 

Za integral oblika ( – prirodni broj) izvodimo ponavljajući formula redukcije:
, Gdje ![]() – integral stupnja niže.
– integral stupnja niže.
Provjerimo valjanost ove formule za riješeni integral.
U ovom slučaju: , , koristimo formulu: 
Kao što vidite, odgovori su isti.
Primjer 14
Nađi neodređeni integral
Ovo je primjer koji trebate sami riješiti. Otopina uzorka koristi gornju formulu dva puta zaredom.
Ako je ispod stupnja nedjeljiv kvadratni trinom, tada se rješenje reducira na binom izdvajanjem savršenog kvadrata, na primjer:
Što ako postoji dodatni polinom u brojniku? U ovom slučaju koristi se metoda neodređenih koeficijenata, a funkcija integranda se proširuje u zbroj razlomaka. Ali u mojoj praksi postoji takav primjer nikad upoznao, pa sam propustio ovaj slučaj u članku Integrali razlomačko-racionalnih funkcija, sad ću to preskočiti. Ako još uvijek naiđete na takav integral, pogledajte udžbenik - tamo je sve jednostavno. Mislim da nije preporučljivo uključiti materijal (čak ni jednostavan), čija je vjerojatnost susreta ravna nuli.
Integriranje složenih trigonometrijskih funkcija
Pridjev "složen" za većinu je primjera opet uglavnom uvjetan. Počnimo s tangensima i kotangensima u velikim potencijama. Sa stajališta korištenih metoda rješavanja, tangens i kotangens su gotovo iste stvari, pa ću više govoriti o tangensu, implicirajući da demonstrirana metoda za rješavanje integrala vrijedi i za kotangens.
U gornjoj lekciji koju smo pogledali univerzalna trigonometrijska supstitucija za rješavanje određene vrste integrala trigonometrijskih funkcija. Nedostatak univerzalne trigonometrijske supstitucije je ta što njezina uporaba često rezultira glomaznim integralima s teškim izračunima. A u nekim slučajevima, univerzalna trigonometrijska zamjena se može izbjeći!
Razmotrimo još jedan kanonski primjer, integral jednog podijeljenog sa sinusom:
Primjer 17
Nađi neodređeni integral
Ovdje možete upotrijebiti univerzalnu trigonometrijsku zamjenu i dobiti odgovor, ali postoji racionalniji način. Dat ću cjelovito rješenje s komentarima za svaki korak:

(1) Koristimo trigonometrijsku formulu za sinus dvostrukog kuta.
(2) Izvodimo umjetnu transformaciju: Podijelimo nazivnik i pomnožimo s .
(3) Koristeći poznatu formulu u nazivniku, transformiramo razlomak u tangentu.
(4) Funkciju dovodimo pod predznak diferencijala.
(5) Uzmite integral.
Nekoliko jednostavnih primjera koje možete riješiti sami:
Primjer 18
Nađi neodređeni integral
Napomena: Prvi korak trebao bi biti korištenje formule redukcije ![]() i pažljivo izvršite radnje slične prethodnom primjeru.
i pažljivo izvršite radnje slične prethodnom primjeru.
Primjer 19
Nađi neodređeni integral
Pa, ovo je vrlo jednostavan primjer.
Potpuna rješenja i odgovori na kraju lekcije.
Mislim da sada nitko neće imati problema s integralima: ![]() i tako dalje.
i tako dalje.
Koja je ideja metode? Ideja je koristiti transformacije i trigonometrijske formule za organiziranje samo tangenti i derivacije tangensa u integrand. Odnosno, govorimo o zamjeni: ![]() . U primjerima 17-19 zapravo smo koristili ovu zamjenu, ali integrali su bili toliko jednostavni da smo prošli s ekvivalentnom radnjom - podvođenjem funkcije pod diferencijalni predznak.
. U primjerima 17-19 zapravo smo koristili ovu zamjenu, ali integrali su bili toliko jednostavni da smo prošli s ekvivalentnom radnjom - podvođenjem funkcije pod diferencijalni predznak.
Slično razmišljanje, kao što sam već spomenuo, može se izvesti za kotangens.
Postoji i formalni preduvjet za primjenu gore navedene zamjene:
Zbroj potencija kosinusa i sinusa je negativan cijeli PARNI broj, Na primjer:
za integral – negativan cijeli PARNI broj.
! Bilješka : ako integrand sadrži SAMO sinus ili SAMO kosinus, onda se i integral uzima za negativan neparni stupanj (najjednostavniji slučajevi su u primjerima br. 17, 18).
Pogledajmo nekoliko smislenijih zadataka temeljenih na ovom pravilu:
Primjer 20
Nađi neodređeni integral
Zbroj potencija sinusa i kosinusa: 2 – 6 = –4 je negativan cijeli PARNI broj, što znači da se integral može svesti na tangente i njegovu derivaciju: 
(1) Transformirajmo nazivnik.
(2) Korištenjem poznate formule dobivamo .
(3) Transformirajmo nazivnik.
(4) Koristimo formulu ![]() .
.
(5) Funkciju dovodimo pod predznak diferencijala.
(6) Vršimo zamjenu. Iskusniji učenici možda neće izvršiti zamjenu, ali ipak je bolje zamijeniti tangentu jednim slovom - manji je rizik od zabune.
Primjer 21
Nađi neodređeni integral
Ovo je primjer koji trebate sami riješiti.
Držite se, prvenstvene runde uskoro počinju =)
Često integrand sadrži "mešanicu":
Primjer 22
Nađi neodređeni integral ![]()
Ovaj integral u početku sadrži tangentu, što odmah dovodi do već poznate misli:

Umjetnu transformaciju ostavit ću na samom početku i preostale korake bez komentara, jer je sve već raspravljeno gore.
Nekoliko kreativnih primjera za vlastito rješenje:
Primjer 23
Nađi neodređeni integral ![]()
Primjer 24
Nađi neodređeni integral ![]()
Da, u njima, naravno, možete smanjiti ovlasti sinusa i kosinusa i koristiti univerzalnu trigonometrijsku zamjenu, ali rješenje će biti puno učinkovitije i kraće ako se provodi kroz tangente. Potpuno rješenje i odgovori na kraju lekcije
U praksi je često potrebno izračunati integrale transcendentnih funkcija koje sadrže trigonometrijske funkcije. Kao dio ovog materijala, opisat ćemo glavne vrste funkcija integranda i pokazati koje se metode mogu koristiti za njihovu integraciju.
Integriranje sinusa, kosinusa, tangensa i kotangensa
Počnimo s metodama integriranja osnovnih trigonometrijskih funkcija - sin, cos, t g, c t g. Koristeći tablicu antiderivacija odmah pišemo da je ∫ sin x d x = - cos x + C, a ∫ cos x d x = sin x + C.
Za izračun neodređenih integrala funkcija t g i c t g, možete koristiti predznak diferencijala:
∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C
Kako smo dobili formule ∫ d x sin x = ln 1 - cos x sin x + C i ∫ d x cos x = ln 1 + sin x cos x + C, preuzete iz tablice antiderivacija? Objasnimo samo jedan slučaj, jer će drugi biti jasan analogijom.
Metodom supstitucije pišemo:
∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2
Ovdje trebamo integrirati iracionalnu funkciju. Koristimo istu metodu zamjene:
∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = ∫ d z z 2 - 1 = ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C
Sada vršimo obrnutu zamjenu z = 1 - t 2 i t = sin x:
∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C
Posebno ćemo analizirati slučajeve s integralima koji sadrže potencije trigonometrijskih funkcija, kao što su ∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x.
O tome kako ih ispravno izračunati možete pročitati u članku o integraciji pomoću formula ponavljanja. Ako znate kako su te formule izvedene, lako možete uzeti integrale poput ∫ sin n x · cos m x d x s prirodnim m i n.
Ako imamo kombinaciju trigonometrijskih funkcija s polinomima ili eksponencijalnim funkcijama, tada će se one morati integrirati po dijelovima. Preporučujemo čitanje članka posvećenog metodama za pronalaženje integrala ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a · x · cos (a x) d x .
Najteži su zadaci u kojima integrand uključuje trigonometrijske funkcije s različitim argumentima. Da biste to učinili, morate koristiti osnovne trigonometrijske formule, pa ih je poželjno zapamtiti ili imati pri ruci bilješku.
Primjer 1
Nađite skup antiderivacija funkcije y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) .
Riješenje
Iskoristimo formule za smanjenje stupnja i zapišimo da je cos 2 x 2 = 1 + cos x 2, a cos 2 2 x = 1 + cos 4 x 2. Sredstva,
y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)
U nazivniku imamo formulu za sinus zbroja. Onda to možete napisati ovako:
y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)
Dobili smo zbroj 3 integrala.
∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C
U nekim slučajevima, trigonometrijske funkcije ispod integrala mogu se svesti na frakcijske racionalne izraze korištenjem standardne metode supstitucije. Prvo, uzmimo formule koje izražavaju sin, cos i t g kroz tangens pola argumenta:
sin x = 2 t g x 2 1 + t g 2 x 2, sin x = 1 - t g 2 x 2 1 + t g 2 x 2, t g x = 2 t g x 2 1 - t g 2 x 2
Također ćemo morati izraziti diferencijal d x u smislu tangensa polukuta:
Budući da je d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2, tada
d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2
Dakle, sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 pri z = t g x 2.
Primjer 2
Nađite neodređeni integral ∫ d x 2 sin x + cos x + 2 .
Riješenje
Koristimo standardnu trigonometrijsku metodu zamjene.
2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3
Dobivamo da je ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .
Sada možemo proširiti integrand na jednostavne razlomke i dobiti zbroj dvaju integrala:
∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = ln z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C
∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C
Odgovor: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C
Važno je primijetiti da one formule koje izražavaju funkcije kroz tangentu pola argumenta nisu identiteti, stoga je rezultirajući izraz ln t g x 2 + 1 t g x 2 + 3 + C skup antiderivacija funkcije y = 1 2; sin x + cos x + 2 samo na domeni definicije.
Za rješavanje drugih vrsta problema možete koristiti osnovne metode integracije.
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter
Za integraciju racionalnih funkcija oblika R(sin x, cos x) koristi se supstitucija, koja se naziva univerzalna trigonometrijska supstitucija. Zatim . Univerzalna trigonometrijska supstitucija često rezultira velikim izračunima. Stoga, kad god je moguće, koristite sljedeće zamjene. ![]()
Integracija funkcija racionalno ovisnih o trigonometrijskim funkcijama
1. Integrali oblika ∫ sin n xdx , ∫ cos n xdx , n>0a) Ako je n neparan, tada jednu potenciju sinx (ili cosx) treba unijeti pod predznak diferencijala, a s preostale parne potence prijeći na suprotnu funkciju.
b) Ako je n paran, tada koristimo formule za smanjenje stupnja
2. Integrali oblika ∫ tg n xdx , ∫ ctg n xdx , gdje je n cijeli broj.
Moraju se koristiti formule
3. Integrali oblika ∫ sin n x cos m x dx
a) Neka su m i n različitih pariteta. Koristimo zamjenu t=sin x ako je n neparan ili t=cos x ako je m neparan.
b) Ako su m i n parni, tada koristimo formule za smanjenje stupnja
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integrali oblika
Ako su brojevi m i n iste parnosti, tada koristimo zamjenu t=tg x. Često je prikladno koristiti tehniku trigonometrijske jedinice.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx
Upotrijebimo formule za pretvaranje umnoška trigonometrijskih funkcija u njihov zbroj:
- sin α cos β = ½(sin(α+β)+sin(α-β))
- cos α cos β = ½(cos(α+β)+cos(α-β))
- sin α sin β = ½(cos(α-β)-cos(α+β))
Primjeri
1. Izračunajte integral ∫ cos 4 x·sin 3 xdx .
Napravimo zamjenu cos(x)=t. Tada je ∫ cos 4 x sin 3 xdx = ![]()
![]()
2. Izračunajte integral.
Izvršivši zamjenu sin x=t , dobivamo
![]()
3. Nađi integral.
Vršimo zamjenu tg(x)=t . Zamjenom, dobivamo
![]()
Integriranje izraza oblika R(sinx, cosx)
Primjer br. 1. Izračunaj integrale: 
Riješenje.
a) Integracija izraza oblika R(sinx, cosx), gdje je R racionalna funkcija sin x i cos x, pretvara se u integrale racionalnih funkcija univerzalnom trigonometrijskom zamjenom tg(x/2) = t.
Onda imamo
Univerzalna trigonometrijska zamjena omogućuje prijelaz s integrala oblika ∫ R(sinx, cosx) dx na integral frakcijske racionalne funkcije, ali često takva zamjena dovodi do glomaznih izraza. Pod određenim uvjetima učinkovite su jednostavnije zamjene:
- Ako je zadovoljena jednakost R(-sin x, cos x) = -R(sin x, cos x)dx, tada se primjenjuje zamjena cos x = t.
- Ako vrijedi jednakost R(sin x, -cos x) = -R(sin x, cos x)dx, tada je supstitucija sin x = t.
- Ako vrijedi jednakost R(-sin x, -cos x) = R(sin x, cos x)dx, tada vrijedi zamjena tgx = t ili ctg x = t.

primijenimo univerzalnu trigonometrijsku zamjenu tg(x/2) = t.
Onda odgovori:
Bit će tu i problema koje ćete sami riješiti, a na koje možete vidjeti odgovore.
Integrand se može pretvoriti iz umnoška trigonometrijskih funkcija u zbroj
Razmotrimo integrale u kojima je integrand umnožak sinusa i kosinusa prvog stupnja od x pomnoženih različitim faktorima, to jest integrale oblika
Korištenje poznatih trigonometrijskih formula
(2)
(3)
(4)
može se svaki od umnožaka u integralima oblika (31) transformirati u algebarski zbroj i integrirati prema formulama
![]() (5)
(5)
![]() (6)
(6)
Primjer 1. Pronaći
![]()
Riješenje. Prema formuli (2) na



Primjer 2. Pronaći integral trigonometrijske funkcije
![]()
Riješenje. Prema formuli (3) na ![]()


![]()
Primjer 3. Pronaći integral trigonometrijske funkcije
![]()
Riješenje. Prema formuli (4) na ![]() dobivamo sljedeću transformaciju integranda:
dobivamo sljedeću transformaciju integranda:

Primjenom formule (6) dobivamo
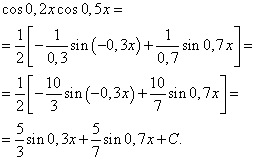
Integral umnoška potencija sinusa i kosinusa istog argumenta
Razmotrimo sada integrale funkcija koje su produkt potencija sinusa i kosinusa istog argumenta, tj.
![]() (7)
(7)
U posebnim slučajevima, jedan od indikatora ( m ili n) može biti nula.
Pri integriranju takvih funkcija koristi se da se parna potencija kosinusa može izraziti kroz sinus, a diferencijal sinusa jednak je cos x dx(ili se čak sinusna potencija može izraziti preko kosinusa, a diferencijal kosinusa je jednak - sin x dx ) .
Treba razlikovati dva slučaja: 1) barem jedan od pokazatelja m I n neparan; 2) oba indikatora su parna.
Neka se dogodi prvi slučaj, naime indikator n = 2k+ 1 - neparno. Zatim, s obzirom na to
![]()
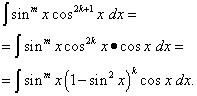
Integrand je prikazan na način da je jedan njegov dio funkcija samo sinusa, a drugi je diferencijal sinusa. Sada koristimo zamjenu varijable t= grijeh x rješenje se svodi na integriranje polinoma s obzirom na t. Kad bi samo diploma mčudan, onda čine isto, izolirajući faktor sin x, izražavajući ostatak integranda u smislu cos x i vjerujući t=cos x. Ova tehnika se također može koristiti kada integrirajući kvocijent potencije sinusa i kosinusa , Kada barem jedan od pokazatelja je neparan . Cijela poanta je u tome kvocijent potencija sinusa i kosinusa poseban je slučaj njihovog umnoška : Kada je trigonometrijska funkcija u nazivniku integranda, njezin je stupanj negativan. Ali postoje i slučajevi parcijalnih trigonometrijskih funkcija, kada su njihove potencije samo parne. O njima - u sljedećem odlomku.
Ako oba pokazatelja m I n– čak i pomoću trigonometrijskih formula

smanjiti eksponente sinusa i kosinusa, nakon čega se dobije integral istog tipa kao gore. Stoga integraciju treba nastaviti prema istoj shemi. Ako je jedan od parnih eksponenata negativan, odnosno uzme se u obzir kvocijent parnih potencija sinusa i kosinusa, tada ova shema nije prikladna . Zatim se koristi promjena varijable ovisno o tome kako se integrand može transformirati. Takav slučaj ćemo razmotriti u sljedećem odlomku.
Primjer 4. Pronaći integral trigonometrijske funkcije
![]()
Riješenje. Eksponent kosinusa je neparan. Stoga, zamislimo se
t= grijeh x(Zatim dt=cos x dx ). Onda dobivamo

Vraćajući se na staru varijablu, konačno nalazimo
![]()
Primjer 5. Pronaći integral trigonometrijske funkcije
![]() .
.
Riješenje. Eksponent kosinusa je, kao iu prethodnom primjeru, neparan, ali veći. Zamislimo se
![]()
i napraviti promjenu varijable t= grijeh x(Zatim dt=cos x dx ). Onda dobivamo
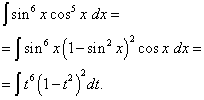
Otvorimo zagrade
![]() i dobivamo
i dobivamo
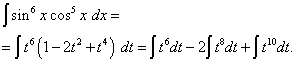
Vraćajući se na staru varijablu, dobivamo rješenje
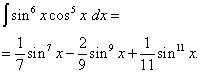
Primjer 6. Pronaći integral trigonometrijske funkcije
![]()
Riješenje. Eksponenti sinusa i kosinusa su parni. Stoga transformiramo funkciju integranda na sljedeći način:

Onda dobivamo
U drugom integralu vršimo promjenu varijable, postavke t= grijeh2 x. Zatim (1/2)dt= cos2 x dx . Stoga,


Napokon dobivamo
![]()
Korištenje metode zamjene varijabli
Metoda zamjene varijabli pri integriranju trigonometrijskih funkcija može se koristiti u slučajevima kada integrand sadrži samo sinus ili samo kosinus, umnožak sinusa i kosinusa, u kojem je sinus ili kosinus na prvom stupnju, tangens ili kotangens, kao i kvocijent parni potencije sinusa i kosinusa jednog te istog argumenta. U ovom slučaju, moguće je izvršiti permutacije ne samo grijeh x = t i grijeh x = t, ali i tg x = t i ctg x = t .
Primjer 8. Pronaći integral trigonometrijske funkcije
![]() .
.
Riješenje. Promijenimo varijablu: , zatim . Rezultirajući integrand može se lako integrirati pomoću tablice integrala:
![]() .
.
![]()
Primjer 9. Pronaći integral trigonometrijske funkcije
Riješenje. Pretvorimo tangens u omjer sinusa i kosinusa:
Promijenimo varijablu: , zatim . Rezultirajući integrand je stolni integral sa znakom minus:
![]() .
.
Vraćajući se na izvornu varijablu, konačno dobivamo:
![]() .
.
Primjer 10. Pronaći integral trigonometrijske funkcije
Riješenje. Promijenimo varijablu: , zatim .
Transformirajmo integrand da primijenimo trigonometrijski identitet ![]() :
:
Mijenjamo varijablu, ne zaboravljajući staviti znak minus ispred integrala (vidi gore, što je jednako dt). Zatim faktoriziramo integrand i integriramo prema tablici:
Vraćajući se na izvornu varijablu, konačno dobivamo:
![]() .
.
Nađite sami integral trigonometrijske funkcije, a zatim pogledajte rješenje
Univerzalna trigonometrijska supstitucija
Univerzalna trigonometrijska supstitucija može se koristiti u slučajevima kada integrand ne spada u slučajeve razmotrene u prethodnim paragrafima. U osnovi, kada je sinus ili kosinus (ili oboje) u nazivniku razlomka. Dokazano je da se sinus i kosinus mogu zamijeniti drugim izrazom koji sadrži tangens polovice izvornog kuta kako slijedi:
Ali imajte na umu da univerzalna trigonometrijska supstitucija često uključuje prilično složene algebarske transformacije, pa je najbolje koristiti kada nijedna druga metoda ne funkcionira. Pogledajmo primjere gdje se uz univerzalnu trigonometrijsku zamjenu koristi zamjena pod diferencijalnim predznakom i metoda neodređenih koeficijenata.
Primjer 12. Pronaći integral trigonometrijske funkcije
![]() .
.
Riješenje. Riješenje. Iskoristimo univerzalna trigonometrijska supstitucija. Zatim  .
.
Razlomke u brojniku i nazivniku pomnožimo s , a dva izbacimo i stavimo ispred znaka integrala. Zatim




