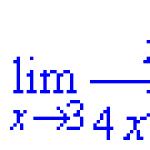Teoria limitelor- una dintre secțiunile analizei matematice pe care unii o pot stăpâni, în timp ce alții au dificultăți în calcularea limitelor. Întrebarea găsirii limitelor este destul de generală, deoarece există zeci de tehnici limite de soluție tipuri variate. Aceleași limite pot fi găsite atât folosind regula lui L'Hopital, cât și fără ea. Se întâmplă ca programarea unei serii de funcții infinitezimale vă permite să obțineți rapid rezultatul dorit. Există un set de tehnici și trucuri care vă permit să găsiți limita unei funcții de orice complexitate. În acest articol vom încerca să înțelegem principalele tipuri de limite care sunt cel mai des întâlnite în practică. Nu vom da aici teoria și definiția limitei; există multe resurse pe Internet unde se discută acest lucru. Prin urmare, să trecem la calcule practice, aici este locul în care „Nu știu! Nu pot! Nu am fost învățați!”

Calcularea limitelor folosind metoda substituției

Exemplul 1. Găsiți limita unei funcții
Lim((x^2-3*x)/(2*x+5),x=3).
Rezolvare: Exemple de acest fel pot fi calculate teoretic folosind substituția obișnuită

Limita este 18/11.
Nu este nimic complicat sau înțelept în legătură cu astfel de limite - am înlocuit valoarea, am calculat-o și am notat limita ca răspuns. Cu toate acestea, pe baza unor astfel de limite, toată lumea este învățată că, în primul rând, trebuie să înlocuiască valoarea în funcție. În plus, limitele devin mai complicate, introducând conceptul de infinit, incertitudine și altele asemenea.

O limită cu incertitudine ca infinitul împărțit la infinit. Tehnici de dezvăluire a incertitudinii

Exemplul 2. Găsiți limita unei funcții
Lim((x^2+2x)/(4x^2+3x-4),x=infinit).
Rezolvare: este dată o limită a formei polinom împărțită la un polinom, iar variabila tinde spre infinit

Pur și simplu înlocuirea valorii la care ar trebui găsită variabila pentru a găsi limitele nu va ajuta, obținem o incertitudine de forma infinit împărțită la infinit.
Conform teoriei limitelor, algoritmul de calcul al limitei este de a găsi cea mai mare putere a lui „x” în numărător sau numitor. În continuare, numărătorul și numitorul sunt simplificați la acesta și se găsește limita funcției

Deoarece valoarea tinde spre zero atunci când variabila se apropie de infinit, acestea sunt neglijate sau sunt scrise în expresia finală sub formă de zerouri.

Imediat din practică, puteți obține două concluzii care sunt un indiciu în calcule. Dacă o variabilă tinde spre infinit și gradul numărătorului este mai mare decât gradul numitorului, atunci limita este egală cu infinitul. În caz contrar, dacă polinomul din numitor este de ordin mai mare decât în numărător, limita este zero.
Limita poate fi scrisă în formule ca aceasta:

Dacă avem o funcție de forma unui câmp obișnuit fără fracții, atunci limita sa este egală cu infinitul

Următorul tip de limite se referă la comportamentul funcțiilor aproape de zero.

Exemplul 3. Găsiți limita unei funcții
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Soluție: Nu este nevoie să eliminați aici factorul conducător al polinomului. Exact invers, trebuie să găsiți cea mai mică putere a numărătorului și numitorului și să calculați limita

Valoarea x^2; x tinde spre zero atunci când variabila tinde spre zero. Prin urmare, ele sunt neglijate, așa că obținem

că limita este 2,5.

Acum știi cum să găsiți limita unei funcții din formă, împărțiți un polinom la un polinom dacă variabila tinde spre infinit sau 0. Dar aceasta este doar o mică și ușoară parte a exemplelor. Din următorul material veți învăța cum să descoperiți incertitudinile în limitele unei funcții.

Limită cu incertitudine de tip 0/0 și metode de calcul a acesteia

Toată lumea își amintește imediat regula că nu poți împărți la zero. Totuși, teoria limitelor în acest context implică funcții infinitezimale.
Să ne uităm la câteva exemple pentru claritate.

Exemplul 4. Găsiți limita unei funcții
Lim((3x^2+10x+7)/(x+1), x=-1).
Rezolvare: Când înlocuim valoarea variabilei x = -1 în numitor, obținem zero și obținem același lucru la numărător. Deci avem incertitudinea formei 0/0.
Abordarea unei astfel de incertitudini este simplă: trebuie să factorizați polinomul sau, mai degrabă, să selectați factorul care transformă funcția în zero.

După extindere, limita funcției poate fi scrisă ca

Aceasta este întreaga metodă de calcul a limitei unei funcții. Facem același lucru dacă există o limită a formei polinom împărțit la un polinom.

Exemplul 5. Găsiți limita unei funcții
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Soluție: Substituirea directă arată
2*4-7*2+6=0;
3*4-2-10=0
ce avem incertitudine de tip 0/0.
Să împărțim polinoamele la factorul care introduce singularitatea

Există profesori care învață că polinoamele de ordinul 2, adică de tipul „ecuații pătratice”, trebuie rezolvate prin discriminant. Dar practica reală arată că acest lucru este mai lung și mai confuz, așa că scăpați de caracteristicile în limitele algoritmului specificat. Astfel, scriem funcția sub formă de factori simpli și o calculăm în limită

După cum puteți vedea, nu este nimic complicat în calcularea unor astfel de limite. Până când studiezi limitele, știi să împarți polinoamele, cel puțin conform programului pe care ar fi trebuit să-l fi trecut deja.
Printre sarcinile pe incertitudine de tip 0/0 Există unele în care trebuie să utilizați formule de înmulțire abreviate. Dar dacă nu le cunoașteți, atunci împărțind un polinom la un monom puteți obține formula dorită.

Exemplul 6. Găsiți limita unei funcții
Lim((x^2-9)/(x-3), x=3).
Rezolvare: Avem o incertitudine de tip 0/0. La numărător folosim formula de înmulțire prescurtată

și calculați limita necesară

Metodă de dezvăluire a incertitudinii prin înmulțirea cu conjugatul său

Metoda se aplică la limitele în care incertitudinea este generată de funcțiile iraționale. Numătorul sau numitorul se transformă în zero în punctul de calcul și nu se știe cum să se găsească granița.

Exemplul 7. Găsiți limita unei funcții
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Soluţie: Să reprezentăm variabila în formula limită

La substituire, obținem o incertitudine de tip 0/0.
Conform teoriei limitelor, modalitatea de a ocoli această caracteristică este de a multiplica expresia irațională cu conjugatul ei. Pentru a vă asigura că expresia nu se schimbă, numitorul trebuie împărțit la aceeași valoare

Folosind regula diferenței de pătrate, simplificăm numărătorul și calculăm limita funcției

Simplificam termenii care creeaza singularitatea in limita si efectuam substitutia

Exemplul 8. Găsiți limita unei funcții
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Rezolvare: Substituția directă arată că limita are o singularitate de forma 0/0.

Pentru a extinde, înmulțim și împărțim la conjugatul numărătorului

Notăm diferența de pătrate

Simplificam termenii care introduc singularitatea si gasim limita functiei

Exemplul 9. Găsiți limita unei funcții
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Soluție: Înlocuiți doi în formulă

Primim incertitudine 0/0.
Numitorul trebuie înmulțit cu expresia conjugată, iar la numărător trebuie rezolvată sau factorizată ecuația pătratică, ținând cont de singularitate. Deoarece se știe că 2 este o rădăcină, găsim a doua rădăcină folosind teorema lui Vieta

Astfel, scriem numeratorul sub forma

și înlocuiți-l în limită

Prin reducerea diferenței de pătrate, scăpăm de singularitățile din numărător și numitor

În acest fel, puteți scăpa de singularități în multe exemple, iar aplicația trebuie remarcată oriunde o anumită diferență de rădăcini se transformă în zero în timpul înlocuirii. Alte tipuri de limite se referă la funcții exponențiale, funcții infinitezimale, logaritmi, limite speciale și alte tehnici. Dar puteți citi despre acest lucru în articolele enumerate mai jos despre limite.

Funcții elementare și grafice ale acestora.

Principalele funcții elementare sunt: funcția de putere, funcția exponențială, funcția logaritmică, funcțiile trigonometrice și funcțiile trigonometrice inverse, precum și o funcție polinom și o funcție rațională, care este raportul a două polinoame.

Funcțiile elementare includ și acele funcții care se obțin din cele elementare prin aplicarea celor patru operații aritmetice de bază și formarea unei funcții complexe.

Grafice ale funcțiilor elementare

	Linie dreapta- graficul unei funcţii liniare y = ax + b. Funcția y crește monoton pentru a > 0 și scade pentru a< 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)
	Parabolă- graficul funcţiei trinomiale pătratice y = ax 2 + bx + c. Are o axă de simetrie verticală. Dacă a > 0, are un minim dacă a< 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax 2 + bx +c =0
	Hiperbolă- graficul funcției. Când a > O este situat în sferturile I și III, când a< 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а >0) sau y - - x(a< 0).
	Functie exponentiala. Expozant(funcție exponențială la baza e) y = e x. (O altă ortografie y = exp(x)). Asimptota este axa absciselor.
	Funcția logaritmică y = log a x(a > 0)
	y = sinx. Undă sinusoidală- functie periodica cu perioada T = 2π

Limita functiei.

Funcția y=f(x) are un număr A ca limită, deoarece x tinde spre a, dacă pentru orice număr ε › 0 există un număr δ › 0 astfel încât | y – A | ‹ ε dacă |x - a| ‹ δ,

sau lim y = A

Continuitatea funcției.

Funcția y=f(x) este continuă în punctul x = a dacă lim f(x) = f(a), adică.

limita unei funcții într-un punct x = a este egală cu valoarea funcției într-un punct dat.

Găsirea limitelor funcțiilor.

Teoreme de bază privind limitele funcțiilor.

1. Limita unei valori constante este egală cu această valoare constantă:

2. Limita unei sume algebrice este egală cu suma algebrică a limitelor acestor funcții:

lim (f + g - h) = lim f + lim g - lim h

3. Limita produsului mai multor funcții este egală cu produsul limitelor acestor funcții:

lim (f * g* h) = lim f * lim g * lim h

4. Limita câtului a două funcții este egală cu câtul limitelor acestor funcții dacă limita numitorului nu este egală cu 0:

lim------- = ----------

Prima limită remarcabilă: lim --------- = 1

A doua limită remarcabilă: lim (1 + 1/x) x = e (e = 2, 718281..)

Exemple de găsire a limitelor funcțiilor.

5.1. Exemplu:

Orice limită constă din trei părți:

1) Cunoscuta pictogramă limită.

2) Intrări sub pictograma limită. Intrarea scrie „X tinde spre unu”. Cel mai adesea este x, deși în loc de „x” poate exista orice altă variabilă. În locul unu poate fi absolut orice număr, precum și infinitul 0 sau .

3) Funcții sub semnul limită, în acest caz .

Înregistrarea în sine se citește astfel: „limita unei funcții ca x tinde spre unitate”.

O întrebare foarte importantă - ce înseamnă expresia „x”? se straduieste catre unul"? expresia „x” se straduieste la unu” ar trebui înțeles astfel: „x” preia constant valorile care se apropie de unitatea infinit apropiată și practic coincid cu ea.

Cum se rezolvă exemplul de mai sus? Pe baza celor de mai sus, trebuie doar să înlocuiți unul în funcție de sub semnul limită:

Deci prima regulă : Când vi se oferă o limită, mai întâi conectați pur și simplu numărul în funcție.

5.2. Exemplu cu infinit:

Să ne dăm seama ce este? Acesta este cazul când crește fără limită.

Astfel, dacă , apoi funcția tinde spre minus infinit:

Conform primei noastre reguli, în loc de „X” înlocuim în funcție infinit și obținem răspunsul.

5.3. Un alt exemplu cu infinit:

Din nou începem să creștem la infinit și să ne uităm la comportamentul funcției.
Concluzie: funcția crește nelimitat

5.4. O serie de exemple:

Încercați să analizați mental următoarele exemple și să rezolvați cele mai simple tipuri de limite:

, , , , , , , , ,

Ce trebuie să rețineți și să înțelegeți din cele de mai sus?

Când se oferă o limită, mai întâi conectați pur și simplu numărul în funcție. În același timp, trebuie să înțelegeți și să rezolvați imediat cele mai simple limite, cum ar fi , , etc.

6. Limite cu incertitudine de tip și o metodă de rezolvare a acestora.

Acum vom lua în considerare grupul de limite când , iar funcția este o fracție al cărei numărător și numitor conțin polinoame.

6.1. Exemplu:

Calculați limita

Conform regulii noastre, încercăm să substituim infinitul în funcție. Ce obținem în vârf? Infinit. Și ce se întâmplă mai jos? De asemenea, infinitul. Astfel, avem ceea ce se numește incertitudinea speciei. S-ar putea crede că = 1, iar răspunsul este gata, dar în cazul general nu este deloc cazul și trebuie să aplicați o tehnică de soluție, pe care o vom lua în considerare acum.

Cum se rezolvă limitele de acest tip?

Mai întâi ne uităm la numărător și găsim cea mai mare putere:

Puterea principală în numărător este două.

Acum ne uităm la numitor și îl găsim și la cea mai mare putere:

Cel mai înalt grad al numitorului este doi.

Apoi alegem cea mai mare putere a numărătorului și numitorului: în acest exemplu, acestea sunt aceleași și egale cu doi.

Deci, metoda de rezolvare este următoarea: pentru a dezvălui incertitudinea trebuie să împărțiți numărătorul și numitorul cu în gradul superior.

Astfel, răspunsul nu este 1.

Exemplu

Găsiți limita

Din nou la numărător și numitor găsim în cel mai înalt grad:

Gradul maxim la numărător: 3

Gradul maxim la numitor: 4

Alege cel mai mare valoare, în acest caz patru.
Conform algoritmului nostru, pentru a dezvălui incertitudinea, împărțim numărătorul și numitorul la .

Exemplu

Găsiți limita

Gradul maxim de „X” la numărător: 2

Gradul maxim de „X” la numitor: 1 (se poate scrie ca)
Pentru a dezvălui incertitudinea, este necesar să împărțiți numărătorul și numitorul la . Soluția finală ar putea arăta astfel:

Împărțiți numărătorul și numitorul la

Soluţie limitele funcției online. Găsiți valoarea limită a unei funcții sau a secvenței funcționale într-un punct, calculați final valoarea funcției la infinit. determinarea convergenței unei serii de numere și multe altele se poate face datorită serviciului nostru online -. Vă permitem să găsiți limitele funcțiilor online rapid și precis. Dumneavoastră introduceți variabila funcție și limita la care tinde aceasta, iar serviciul nostru efectuează toate calculele pentru dvs., oferind un răspuns precis și simplu. Si pentru găsirea limitei online puteți introduce atât serii numerice, cât și funcții analitice care conțin constante în expresie literală. În acest caz, limita găsită a funcției va conține aceste constante ca argumente constante în expresie. Serviciul nostru rezolvă orice probleme complexe de găsire limite online, este suficient să indicați funcția și punctul în care este necesar să se calculeze valoarea limită a funcției. De calculat limitele online, puteți folosi diverse metode și reguli de rezolvare a acestora, verificând în același timp rezultatul obținut cu rezolvarea limitelor online pe www.site-ul, ceea ce va duce la îndeplinirea cu succes a sarcinii - veți evita propriile greșeli și erori de scris. Sau puteți avea încredere completă în noi și folosiți rezultatul nostru în munca dvs., fără a cheltui efort și timp suplimentar pentru a calcula în mod independent limita funcției. Permitem introducerea de valori limită, cum ar fi infinitul. Este necesar să introduceți un membru comun al unei secvențe de numere și www.site va calcula valoarea limita online la plus sau minus infinit.

Unul dintre conceptele de bază ale analizei matematice este limita functieiȘi limită de secvență la un punct și la infinit, este important să poți rezolva corect limite. Cu serviciul nostru acest lucru nu va fi dificil. Se ia o decizie limite onlineîn câteva secunde, răspunsul este corect și complet. Studiul analizei matematice începe cu trecerea la limită, limite sunt folosite în aproape toate domeniile matematicii superioare, așa că este util să aveți un server la îndemână pentru soluții limită online, care este site-ul.

Ne-am dat seama de funcțiile elementare de bază.

Când trecem la funcții de tip mai complex, cu siguranță vom întâlni apariția unor expresii al căror sens nu este definit. Astfel de expresii sunt numite incertitudini.

Să enumerăm totul principalele tipuri de incertitudini: zero împărțit la zero (0 cu 0), infinit împărțit la infinit, zero înmulțit cu infinit, infinit minus infinit, unu la puterea infinitului, zero la puterea lui zero, infinitul la puterea zero.

TOATE CELALALTE EXPRIMI ALE INCERTITUDINEI NU SUNT ȘI IAU O VALOARE FINITĂ SAU INFINITĂ COMPLET SPECIFĂ.

Descoperiți incertitudinea permite:

simplificarea tipului de funcție (transformarea expresiilor folosind formule de înmulțire prescurtate, formule trigonometrice, înmulțire prin expresii conjugate urmate de reducere etc.);
utilizarea unor limite remarcabile;
aplicarea regulii lui L'Hopital;
folosind înlocuirea unei expresii infinitezimale cu echivalentul acesteia (folosind un tabel de infinitezimale echivalente).

Să grupăm incertitudinile în tabelul de incertitudine. Pentru fiecare tip de incertitudine asociem o metodă de dezvăluire a acesteia (metoda de găsire a limitei).

Acest tabel, împreună cu tabelul limitelor funcțiilor elementare de bază, vor fi instrumentele principale în găsirea oricăror limite.

Să dăm câteva exemple când totul funcționează imediat după înlocuirea valorii și nu apare incertitudinea.

Exemplu.

Calculați limita

Soluţie.

Înlocuiți valoarea:

Și am primit imediat un răspuns.

Răspuns:

Exemplu.

Calculați limita

Soluţie.

Inlocuim valoarea x=0 in baza functiei noastre de putere exponentiala:

Adică limita poate fi rescrisă ca

Acum să aruncăm o privire la indicator. Aceasta este o funcție de putere. Să ne întoarcem la tabelul de limite pentru funcțiile de putere cu exponent negativ. De acolo avem Și , prin urmare, putem scrie .

Pe baza acestui fapt, limita noastră va fi scrisă astfel:

Ne întoarcem din nou la tabelul limitelor, dar pentru funcții exponențiale cu o bază mai mare decât unu, din care avem:

Răspuns:

Să ne uităm la exemple cu soluții detaliate Descoperirea incertitudinilor prin transformarea expresiilor.

Foarte des, expresia de sub semnul limită trebuie să fie ușor transformată pentru a scăpa de incertitudini.

Exemplu.

Calculați limita

Soluţie.

Înlocuiți valoarea:

Am ajuns la incertitudine. Ne uităm la tabelul de incertitudine pentru a selecta o metodă de soluție. Să încercăm să simplificăm expresia.

Răspuns:

Exemplu.

Calculați limita

Soluţie.

Înlocuiți valoarea:

Am ajuns la incertitudine (0 la 0). Ne uităm la tabelul de incertitudine pentru a alege o metodă de soluție și pentru a încerca să simplificăm expresia. Să înmulțim atât numărătorul, cât și numitorul cu expresia conjugată la numitor.

Pentru numitor expresia conjugată va fi

Am înmulțit numitorul astfel încât să putem aplica formula de înmulțire prescurtată - diferență de pătrate și apoi să reducem expresia rezultată.

După o serie de transformări, incertitudinea a dispărut.

Răspuns:

COMETARIU: Pentru limite de acest tip, metoda de înmulțire prin expresii conjugate este tipică, așa că nu ezitați să o folosiți.

Exemplu.

Calculați limita

Soluţie.

Înlocuiți valoarea:

Am ajuns la incertitudine. Ne uităm la tabelul de incertitudine pentru a alege o metodă de soluție și pentru a încerca să simplificăm expresia. Deoarece atât numărătorul, cât și numitorul dispar la x = 1, atunci dacă aceste expresii pot fi reduse (x-1) și incertitudinea va dispărea.

Să factorizăm numărătorul:

Să factorizăm numitorul:

Limita noastră va lua forma:

După transformare, incertitudinea a fost dezvăluită.

Răspuns:

Să luăm în considerare limitele la infinit din expresiile puterii. Dacă exponenții expresiei puterii sunt pozitivi, atunci limita la infinit este infinită. În plus, cel mai mare grad este de importanță primordială, restul poate fi aruncat.

Exemplu.

Dacă expresia de sub semnul limită este o fracție și atât numărătorul, cât și numitorul sunt expresii de putere (m este puterea numărătorului și n este puterea numitorului), atunci când o incertitudine de forma infinit la infinit apare, în acest caz se dezvăluie incertitudineaîmpărțind atât numărătorul cât și numitorul la

Exemplu.

Calculați limita

Prima limită remarcabilă este următoarea egalitate:

\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)

Deoarece pentru $\alpha\to(0)$ avem $\sin\alpha\to(0)$, se spune că prima limită remarcabilă dezvăluie o incertitudine de forma $\frac(0)(0)$. În general, în formula (1), în locul variabilei $\alpha$, orice expresie poate fi plasată sub semnul sinus și la numitor, atâta timp cât sunt îndeplinite două condiții:

Expresiile de sub semnul sinus și din numitor tind simultan spre zero, adică. există incertitudinea formei $\frac(0)(0)$.
Expresiile de sub semnul sinus și la numitor sunt aceleași.

Corolarele din prima limită remarcabilă sunt, de asemenea, adesea folosite:

\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(ecuație)

Unsprezece exemple sunt rezolvate pe această pagină. Exemplul nr. 1 este dedicat demonstrarii formulelor (2)-(4). Exemplele nr. 2, nr. 3, nr. 4 și nr. 5 conțin soluții cu comentarii detaliate. Exemplele nr. 6-10 conțin soluții practic fără comentarii, deoarece explicațiile detaliate au fost date în exemplele anterioare. Soluția folosește câteva formule trigonometrice care pot fi găsite.

Permiteți-mi să observ că prezența funcțiilor trigonometrice cuplate cu incertitudinea $\frac (0) (0)$ nu înseamnă neapărat aplicarea primei limite remarcabile. Uneori sunt suficiente transformări trigonometrice simple - de exemplu, vezi.

Exemplul nr. 1

Demonstrați că $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

a) Deoarece $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, atunci:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

Deoarece $\lim_(\alpha\to(0))\cos(0)=1$ și $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, Acea:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

b) Să facem schimbarea $\alpha=\sin(y)$. Deoarece $\sin(0)=0$, atunci din condiția $\alpha\to(0)$ avem $y\to(0)$. În plus, există o vecinătate de zero în care $\arcsin\alpha=\arcsin(\sin(y))=y$, deci:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

Egalitatea $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ a fost dovedită.

c) Să facem înlocuirea $\alpha=\tg(y)$. Deoarece $\tg(0)=0$, atunci condițiile $\alpha\to(0)$ și $y\to(0)$ sunt echivalente. În plus, există o vecinătate de zero în care $\arctg\alpha=\arctg\tg(y))=y$, prin urmare, pe baza rezultatelor punctului a), vom avea:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\la(0))\frac(y)(\tg(y)) =\lim_(y\la(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

Egalitatea $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ a fost dovedită.

Egalitățile a), b), c) sunt adesea folosite împreună cu prima limită remarcabilă.

Exemplul nr. 2

Calculați limita $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) ( x+7))$.

Deoarece $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ și $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. si atat numaratorul cat si numitorul fractiei tind simultan spre zero, atunci aici avem de-a face cu o incertitudine de forma $\frac(0)(0)$, i.e. Terminat. În plus, este clar că expresiile de sub semnul sinus și din numitor coincid (adică și este satisfăcut):

Deci, ambele condiții enumerate la începutul paginii sunt îndeplinite. De aici rezultă că formula este aplicabilă, i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.

Răspuns: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.

Exemplul nr. 3

Găsiți $\lim_(x\to(0))\frac(\sin(9x))(x)$.

Deoarece $\lim_(x\to(0))\sin(9x)=0$ și $\lim_(x\to(0))x=0$, atunci avem de-a face cu o incertitudine de forma $\frac (0 )(0)$, adică Terminat. Cu toate acestea, expresiile de sub semnul sinus și din numitor nu coincid. Aici trebuie să ajustați expresia din numitor la forma dorită. Avem nevoie ca expresia $9x$ să fie la numitor, atunci va deveni adevărată. În esență, ne lipsește un factor de 9 USD în numitor, care nu este atât de greu de introdus - doar înmulțiți expresia din numitor cu 9 USD. Desigur, pentru a compensa înmulțirea cu $9$, va trebui să împărțiți imediat la $9$:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$

Acum, expresiile de la numitor și de sub semnul sinus coincid. Ambele condiții pentru limita $\lim_(x\to(0))\frac(\sin(9x))(9x)$ sunt îndeplinite. Prin urmare, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. Și asta înseamnă că:

$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

Răspuns: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

Exemplul nr. 4

Găsiți $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.

Deoarece $\lim_(x\to(0))\sin(5x)=0$ și $\lim_(x\to(0))\tg(8x)=0$, aici avem de-a face cu incertitudinea formei $\frac(0)(0)$. Cu toate acestea, forma primei limite remarcabile este încălcată. Un numărător care conține $\sin(5x)$ necesită un numitor de $5x$. În această situație, cel mai simplu mod este să împărțiți numărătorul cu $5x$ și să înmulțiți imediat cu $5x$. În plus, vom efectua o operație similară cu numitorul, înmulțind și împărțind $\tg(8x)$ la $8x$:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

Reducând cu $x$ și luând constanta $\frac(5)(8)$ în afara semnului limită, obținem:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

Rețineți că $\lim_(x\to(0))\frac(\sin(5x))(5x)$ îndeplinește pe deplin cerințele pentru prima limită remarcabilă. Pentru a găsi $\lim_(x\to(0))\frac(\tg(8x))(8x)$ se aplică următoarea formulă:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$

Răspuns: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.

Exemplul nr. 5

Găsiți $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.

Deoarece $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (rețineți că $\cos(0)=1$) și $\ lim_(x\to(0))x^2=0$, atunci avem de-a face cu incertitudinea de forma $\frac(0)(0)$. Totuși, pentru a aplica prima limită remarcabilă, ar trebui să scăpați de cosinusul din numărător, trecând la sinusuri (pentru a aplica apoi formula) sau tangente (pentru a aplica apoi formula). Acest lucru se poate face cu următoarea transformare:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$

Să revenim la limită:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$

Fracția $\frac(\sin^2(5x))(x^2)$ este deja apropiată de forma necesară pentru prima limită remarcabilă. Să lucrăm puțin cu fracția $\frac(\sin^2(5x))(x^2)$, ajustând-o la prima limită remarcabilă (rețineți că expresiile din numărător și sub sinus trebuie să se potrivească):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$

Să revenim la limita în cauză:

$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$

Răspuns: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

Exemplul nr. 6

Găsiți limita $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.

Deoarece $\lim_(x\to(0))(1-\cos(6x))=0$ și $\lim_(x\to(0))(1-\cos(2x))=0$, atunci avem de-a face cu incertitudinea $\frac(0)(0)$. Să o dezvăluim cu ajutorul primei limite remarcabile. Pentru a face acest lucru, să trecem de la cosinus la sinusuri. Deoarece $1-\cos(2\alpha)=2\sin^2(\alpha)$, atunci:

$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

Trecând la sinusuri în limita dată, vom avea:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) = 9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$

Răspuns: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

Exemplul nr. 7

Calculați limita $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ sub rezerva $\alpha\neq \ beta$.

Explicații detaliate au fost date mai devreme, dar aici pur și simplu observăm că din nou există incertitudine $\frac(0)(0)$. Să trecem de la cosinus la sinus folosind formula

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

Folosind această formulă, obținem:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\dreapta| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta) )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$

Răspuns: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.

Exemplul nr. 8

Găsiți limita $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.

Deoarece $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (rețineți că $\sin(0)=\tg(0)=0$) și $\ lim_(x\to(0))x^3=0$, atunci aici avem de-a face cu incertitudinea de forma $\frac(0)(0)$. Să-l defalcăm după cum urmează:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1) ) =\frac(1)(2). $$

Răspuns: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.

Exemplul nr. 9

Găsiți limita $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.

Deoarece $\lim_(x\to(3))(1-\cos(x-3))=0$ și $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, atunci există incertitudinea formei $\frac(0)(0)$. Înainte de a trece la extinderea acesteia, este convenabil să faceți o schimbare de variabilă în așa fel încât noua variabilă să tinde spre zero (rețineți că în formule variabila $\alpha \to 0$). Cel mai simplu mod este introducerea variabilei $t=x-3$. Cu toate acestea, pentru comoditatea transformărilor ulterioare (acest beneficiu poate fi văzut în cursul soluției de mai jos), merită să faceți următoarea înlocuire: $t=\frac(x-3)(2)$. Remarc că ambele înlocuiri sunt aplicabile în acest caz, doar că a doua înlocuire vă va permite să lucrați mai puțin cu fracții. Din moment ce $x\la(3)$, atunci $t\la(0)$.

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\dreapta| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

Răspuns: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.

Exemplul nr. 10

Găsiți limita $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2)$.

Încă o dată avem de-a face cu incertitudinea $\frac(0)(0)$. Înainte de a trece la extinderea acesteia, este convenabil să faceți o schimbare de variabilă în așa fel încât noua variabilă să tindă spre zero (rețineți că în formule variabila este $\alpha\to(0)$). Cel mai simplu mod este să introduceți variabila $t=\frac(\pi)(2)-x$. Deoarece $x\la\frac(\pi)(2)$, atunci $t\la(0)$:

$$ \lim_(x\la\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\stânga|\frac(0)(0)\dreapta| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$

Răspuns: $\lim_(x\la\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.

Exemplul nr. 11

Găsiți limitele $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

În acest caz nu trebuie să folosim prima limită minunată. Vă rugăm să rețineți că atât prima cât și a doua limită conțin numai funcții și numere trigonometrice. Adesea în exemple de acest fel este posibilă simplificarea expresiei situate sub semnul limită. Mai mult, după simplificarea și reducerea menționată mai sus a unor factori, incertitudinea dispare. Am dat acest exemplu doar cu un singur scop: să arăt că prezența funcțiilor trigonometrice sub semnul limită nu înseamnă neapărat utilizarea primei limite remarcabile.

Deoarece $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (rețineți că $\sin\frac(\pi)(2)=1$ ) și $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (permiteți-mi să vă reamintesc că $\cos\frac(\pi)(2)=0$), atunci avem care se ocupă de incertitudinea formei $\frac(0)(0)$. Totuși, asta nu înseamnă că va trebui să folosim prima limită minunată. Pentru a dezvălui incertitudinea, este suficient să luăm în considerare faptul că $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\la\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$

Există o soluție similară în cartea de soluții a lui Demidovich (nr. 475). În ceea ce privește a doua limită, ca și în exemplele anterioare din această secțiune, avem o incertitudine de forma $\frac(0)(0)$. De ce apare? Apare deoarece $\tg\frac(2\pi)(3)=-\sqrt(3)$ și $2\cos\frac(2\pi)(3)=-1$. Folosim aceste valori pentru a transforma expresiile în numărător și numitor. Scopul acțiunilor noastre este de a nota suma în numărător și numitor ca produs. Apropo, adesea în cadrul unui tip similar este convenabil să se schimbe o variabilă, făcută în așa fel încât noua variabilă să tinde spre zero (vezi, de exemplu, exemplele nr. 9 sau nr. 10 de pe această pagină). Totuși, în acest exemplu nu are rost să înlocuiești, deși, dacă se dorește, înlocuirea variabilei $t=x-\frac(2\pi)(3)$ nu este dificil de implementat.

$$ \lim_(x\la\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ la\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\la\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$

După cum puteți vedea, nu a trebuit să aplicăm prima limită minunată. Desigur, puteți face acest lucru dacă doriți (vezi nota de mai jos), dar nu este necesar.

Care este soluția folosind prima limită remarcabilă? arată ascunde

Folosind prima limită remarcabilă obținem:

$$ \lim_(x\la\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ dreapta))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3)) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$

Răspuns: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\la\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.