Fie ca punctele M 1, M 2, M 3 să nu se afle pe aceeași dreaptă. După cum se știe, trei astfel de puncte definesc unic un anumit plan p (Fig. 199).
Să derivăm ecuația planului R. Fie M un punct arbitrar în spațiu. Evident, punctul M aparține planului R dacă şi numai dacă vectorii
\(\overrightarrow(M_(1)M)\), \(\overrightarrow(M_(1)M_2)\), \(\overrightarrow(M_(1)M_3)\) sunt coplanare. O condiție necesară și suficientă pentru coplanaritatea a trei vectori este ca produsul lor mixt să fie egal cu zero (§ 23*, Teorema 2). Prin urmare, ecuația unui plan care trece prin trei puncte care nu se află pe aceeași dreaptă poate fi scrisă după cum urmează:
(\(\overrightarrow(M_(1)M)\), \(\overrightarrow(M_(1)M_2)\), \(\overrightarrow(M_(1)M_3)\)) = 0. (1)
Dacă punctele M 1 , M 2 și M 3 sunt date coordonate într-un sistem de coordonate carteziene dreptunghiulare, atunci ecuația (1) poate fi scrisă în coordonate.
Fie M 1 ( X 1 ; y 1 ; z 1), M 2 ( X 2 ; la 2 ; z 2), M 3 ( X 3 ; la 3 ; z 3) - date punct. Să notăm coordonatele unui punct arbitrar M din planul p cu X yȘi z. Să găsim coordonatele vectorilor incluși în ecuația (1):
\(\overrightarrow(M_(1)M)\) = ( x - x 1 ; y - y 1 ; Z Z 1),
\(\overrightarrow(M_(1)M_2)\) = ( X 2 - X 1 ; y 2 -y 1 ; z 2 -z 1),
\(\overrightarrow(M_(1)M_3)\) = ( X 3 - X 1 ; la 3 -y 1 ; z 3 -z 1).
Produsul mixt a trei vectori este egal cu determinantul de ordinul trei, ale cărui linii conțin coordonatele vectorilor. Prin urmare, ecuația (1) în coordonate are forma
$$ \begin(vmatrix) x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \end(vmatrix)= 0 \;\; (2)$$
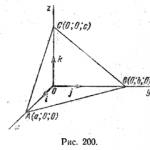
Să găsim ecuația unui plan care trece prin trei puncte A ( A; 0; 0), B(0; b; 0), C(0; 0; Cu), care A =/= 0, b =/= 0, c=/= 0. Aceste puncte se află pe axele de coordonate (Fig. 200).

Presupunând în ecuația (2) X 1 = A, la 1 = 0, z 1 = 0, X 2 = 0, la 2 = b, z 2 = 0, X 3 = 0, la 3 = 0, z 3 = Cu, primim
$$ \begin(vmatrix) x-a & y & z \\ -a & b & 0 \\ -a & 0 & c \end(vmatrix)=0 $$
Expandând determinantul în elementele primului rând, obținem ecuația
bc(x - a) + acy + abz = 0
bcx + asu + abz = abc,
X / A + y / b + z / c = 1. (3)
Ecuația (3) se numește ecuația planului în segmente, din moment ce numerele a, bȘi Cu indicați ce segmente le decupează planul pe axele de coordonate.
Sarcină. Scrieți ecuația planului care trece prin punctele M 1 (-1; 4; -1), M 2 (-13; 2; -10), M 3 (6; 0; 12). Simplificați ecuația rezultată. Obține ecuația unui plan dat în segmente.
Ecuația (2) în acest caz se scrie după cum urmează:
$$ \begin(vmatrix) x+1 & y-4 & z+1 \\ -12 & -2 & -9 \\ 7 & -4 & 13 \end(vmatrix)=0 $$
Aceasta este ecuația acestui plan. Extinderea determinantului de-a lungul primului rând, obținem
62(X+ 1) +93(y- 4)+ 62 (z + 1) = 0,
2X + 3y + 2z - 12 = 0.
Împărțind termen cu termen la 12 și mutând termenul liber al ecuației în partea dreaptă, obținem ecuația acestui plan în segmente
$$ \frac(x)(-6)+\frac(y)(4)+\frac(z)(6)=1 $$
Din ecuație este clar că acest plan decupează segmente de pe axele de coordonate ale căror lungimi sunt egale cu 6, 4 și, respectiv, 6. Oh intersectează planul într-un punct cu o abscisă negativă, axa OU- într-un punct cu ordonată pozitivă, axă Oz- într-un punct cu aplicație pozitivă.
În această lecție ne vom uita la cum să folosim determinantul pentru a crea ecuația plană. Dacă nu știți ce este un determinant, mergeți la prima parte a lecției - „Matrici și determinanți”. Altfel, riști să nu înțelegi nimic din materialul de astăzi.
Ecuația unui plan folosind trei puncte
De ce avem nevoie de o ecuație plană? Este simplu: știind asta, putem calcula cu ușurință unghiuri, distanțe și alte prostii în problema C2. În general, nu te poți descurca fără această ecuație. Prin urmare, formulăm problema:
Sarcină. În spațiu sunt date trei puncte care nu se află pe aceeași linie. Coordonatele lor:
M = (x 1, y 1, z 1);
N = (x 2, y 2, z 2);
K = (x 3, y 3, z 3);Trebuie să creați o ecuație pentru avionul care trece prin aceste trei puncte. În plus, ecuația ar trebui să arate astfel:
Ax + By + Cz + D = 0
unde numerele A, B, C și D sunt coeficienții care, de fapt, trebuie găsiți.
Ei bine, cum să obțineți ecuația unui plan dacă sunt cunoscute doar coordonatele punctelor? Cel mai simplu mod este să înlocuiți coordonatele în ecuația Ax + By + Cz + D = 0. Obțineți un sistem de trei ecuații care pot fi rezolvate cu ușurință.
Mulți studenți consideră această soluție extrem de obositoare și nesigură. Examenul de stat unificat de matematică de anul trecut a arătat că probabilitatea de a face o eroare de calcul este foarte mare.
Prin urmare, cei mai avansați profesori au început să caute soluții mai simple și mai elegante. Și l-au găsit! Adevărat, tehnica obținută se referă mai degrabă la matematica superioară. Personal, a trebuit să răsfoiesc întreaga Listă Federală de Manuale pentru a mă asigura că avem dreptul de a folosi această tehnică fără nicio justificare sau dovezi.
Ecuația unui plan printr-un determinant
Destul de versuri, să trecem la treabă. Pentru început, o teoremă despre modul în care determinantul unei matrice și ecuația planului sunt legate.
Teorema. Fie date coordonatele a trei puncte prin care trebuie trasat planul: M = (x 1, y 1, z 1); N = (x 2, y 2, z 2); K = (x 3, y 3, z 3). Atunci ecuația acestui plan poate fi scrisă prin determinantul:
Ca exemplu, să încercăm să găsim o pereche de avioane care apar de fapt în problemele C2. Uite cât de repede se calculează totul:
A 1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Compunem un determinant și îl echivalăm cu zero:

Extindem determinantul:
a = 1 1 (z − 1) + 0 0 x + (−1) 1 y = z − 1 − y;
b = (−1) 1 x + 0 1 (z − 1) + 1 0 y = −x;
d = a − b = z − 1 − y − (−x ) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
După cum puteți vedea, când am calculat numărul d, am „pieptănat” puțin ecuația, astfel încât variabilele x, y și z să fie în ordinea corectă. Asta e tot! Ecuația plană este gata!
Sarcină. Scrieți o ecuație pentru un plan care trece prin punctele:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Inlocuim imediat coordonatele punctelor in determinant:
Extindem din nou determinantul:
a = 1 1 z + 0 1 x + 1 0 y = z;
b = 1 1 x + 0 0 z + 1 1 y = x + y;
d = a − b = z − (x + y ) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Deci, se obține din nou ecuația planului! Din nou, la ultimul pas a trebuit să schimbăm semnele din el pentru a obține o formulă mai „frumoasă”. Nu este deloc necesar să faceți acest lucru în această soluție, dar este totuși recomandat - pentru a simplifica soluția ulterioară a problemei.
După cum puteți vedea, alcătuirea ecuației unui plan este acum mult mai ușoară. Înlocuim punctele în matrice, calculăm determinantul - și gata, ecuația este gata.
Acest lucru ar putea pune capăt lecției. Cu toate acestea, mulți studenți uită constant ce este în interiorul determinantului. De exemplu, care linie conține x 2 sau x 3 și care linie conține doar x. Pentru a elimina cu adevărat acest lucru, să vedem de unde provine fiecare număr.
De unde vine formula cu determinantul?
Deci, să ne dăm seama de unde vine o ecuație atât de dură cu un determinant. Acest lucru vă va ajuta să vă amintiți și să îl aplicați cu succes.
Toate planurile care apar în problema C2 sunt definite de trei puncte. Aceste puncte sunt întotdeauna marcate pe desen sau chiar indicate direct în textul problemei. În orice caz, pentru a crea o ecuație, va trebui să le notăm coordonatele:
M = (x 1, y 1, z 1);
N = (x 2, y 2, z 2);
K = (x 3, y 3, z 3).
Să luăm în considerare un alt punct din planul nostru cu coordonate arbitrare:
T = (x, y, z)
Luați orice punct din primele trei (de exemplu, punctul M) și trageți vectori din acesta către fiecare dintre cele trei puncte rămase. Obținem trei vectori:
MN = (x 2 − x 1 , y 2 − y 1 , z 2 − z 1 );
MK = (x 3 − x 1 , y 3 − y 1 , z 3 − z 1 );
MT = (x − x 1 , y − y 1 , z − z 1 ).
Acum să compunem o matrice pătrată din acești vectori și să echivalăm determinantul acesteia cu zero. Coordonatele vectorilor vor deveni rânduri ale matricei - și vom obține chiar determinantul care este indicat în teoremă:
Această formulă înseamnă că volumul unui paralelipiped construit pe vectorii MN, MK și MT este egal cu zero. Prin urmare, toți cei trei vectori se află în același plan. În special, un punct arbitrar T = (x, y, z) este exact ceea ce căutam.
Înlocuirea punctelor și dreptelor unui determinant
Determinanții au câteva proprietăți grozave care o fac și mai ușoară rezolvarea problemei C2. De exemplu, nu contează pentru noi din ce punct desenăm vectorii. Prin urmare, următorii determinanți dau aceeași ecuație plană ca cea de mai sus:
De asemenea, puteți schimba liniile determinantului. Ecuația va rămâne neschimbată. De exemplu, multor oameni le place să scrie o linie cu coordonatele punctului T = (x; y; z) în partea de sus. Vă rog, dacă vă este convenabil:
Unii oameni sunt confuzi de faptul că una dintre linii conține variabile x, y și z, care nu dispar la înlocuirea punctelor. Dar nu ar trebui să dispară! Înlocuind numerele în determinant, ar trebui să obțineți această construcție:

Apoi determinantul este extins conform diagramei date la începutul lecției și se obține ecuația standard a planului:
Ax + By + Cz + D = 0
Aruncă o privire la un exemplu. Este ultimul din lecția de astăzi. Voi schimba în mod deliberat liniile pentru a mă asigura că răspunsul va da aceeași ecuație a planului.
Sarcină. Scrieți o ecuație pentru un plan care trece prin punctele:
B1 = (1, 0, 1);
C = (1, 1, 0);
D 1 = (0, 1, 1).
Deci, luăm în considerare 4 puncte:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Mai întâi, să creăm un determinant standard și să-l echivalăm cu zero:
Extindem determinantul:
a = 0 1 (z − 1) + 1 0 (x − 1) + (−1) (−1) y = 0 + 0 + y;
b = (−1) 1 (x − 1) + 1 (−1) (z − 1) + 0 0 y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z ) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;
Asta e, avem răspunsul: x + y + z − 2 = 0.
Acum să rearanjam câteva rânduri în determinant și să vedem ce se întâmplă. De exemplu, să scriem o linie cu variabilele x, y, z nu în partea de jos, ci în partea de sus:
Extindem din nou determinantul rezultat:
a = (x − 1) 1 (−1) + (z − 1) (−1) 1 + y 0 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) 1 0 + y (−1) (−1) + (x − 1) 1 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Avem exact aceeași ecuație plană: x + y + z − 2 = 0. Aceasta înseamnă că într-adevăr nu depinde de ordinea rândurilor. Rămâne doar să scrieți răspunsul.
Deci, suntem convinși că ecuația planului nu depinde de succesiunea de drepte. Putem efectua calcule similare și dovedim că ecuația planului nu depinde de punctul ale cărui coordonate le scadem din alte puncte.
În problema considerată mai sus, am folosit punctul B 1 = (1, 0, 1), dar a fost foarte posibil să luăm C = (1, 1, 0) sau D 1 = (0, 1, 1). În general, orice punct cu coordonate cunoscute se află pe planul dorit.
Poate fi specificat în diferite moduri (un punct și un vector, două puncte și un vector, trei puncte etc.). Având în vedere acest lucru, ecuația plană poate avea forme diferite. De asemenea, în anumite condiții, planurile pot fi paralele, perpendiculare, intersectate etc. Vom vorbi despre asta în acest articol. Vom învăța cum să creăm o ecuație generală a unui plan și nu numai.
Forma normală a ecuației
Să presupunem că există un spațiu R 3 care are un sistem de coordonate XYZ dreptunghiular. Să definim vectorul α, care va fi eliberat din punctul inițial O. Prin capătul vectorului α desenăm un plan P, care va fi perpendicular pe acesta.
Să notăm un punct arbitrar pe P ca Q = (x, y, z). Să semnăm vectorul rază al punctului Q cu litera p. În acest caz, lungimea vectorului α este egală cu р=IαI și Ʋ=(cosα,cosβ,cosγ).
Acesta este un vector unitar care este direcționat în lateral, ca vectorul α. α, β și γ sunt unghiurile care se formează între vectorul Ʋ și direcțiile pozitive ale axelor spațiale x, y, z, respectiv. Proiecția oricărui punct QϵП pe vectorul Ʋ este o valoare constantă care este egală cu p: (p,Ʋ) = p(p≥0).
Ecuația de mai sus are sens când p=0. Singurul lucru este că planul P în acest caz va intersecta punctul O (α=0), care este originea coordonatelor, iar vectorul unitar Ʋ eliberat din punctul O va fi perpendicular pe P, în ciuda direcției sale, care înseamnă că vectorul Ʋ este determinat cu exactitate la semn. Ecuația anterioară este ecuația planului nostru P, exprimată sub formă vectorială. Dar în coordonate va arăta astfel:
P aici este mai mare sau egal cu 0. Am găsit ecuația planului în spațiu în formă normală.
Ecuația generală
Dacă înmulțim ecuația în coordonate cu orice număr care nu este egal cu zero, obținem o ecuație echivalentă cu aceasta, definind chiar acel plan. Va arata asa:

Aici A, B, C sunt numere care sunt simultan diferite de zero. Această ecuație se numește ecuația planului general.
Ecuații de planuri. Cazuri speciale
Ecuația în formă generală poate fi modificată în prezența unor condiții suplimentare. Să ne uităm la unele dintre ele.
Să presupunem că coeficientul A este 0. Aceasta înseamnă că acest plan este paralel cu axa Ox dată. În acest caz, forma ecuației se va schimba: Ву+Cz+D=0.
În mod similar, forma ecuației se va schimba în următoarele condiții:
- În primul rând, dacă B = 0, atunci ecuația se va schimba în Ax + Cz + D = 0, ceea ce va indica paralelismul cu axa Oy.
- În al doilea rând, dacă C=0, atunci ecuația va fi transformată în Ax+By+D=0, ceea ce va indica paralelismul cu axa Oz dată.
- În al treilea rând, dacă D=0, ecuația va arăta ca Ax+By+Cz=0, ceea ce va însemna că planul intersectează O (originea).
- În al patrulea rând, dacă A=B=0, atunci ecuația se va schimba în Cz+D=0, ceea ce se va dovedi paralel cu Oxy.
- În al cincilea rând, dacă B=C=0, atunci ecuația devine Ax+D=0, ceea ce înseamnă că planul către Oyz este paralel.
- În al șaselea rând, dacă A=C=0, atunci ecuația va lua forma Ву+D=0, adică va raporta paralelismul la Oxz.
Tip de ecuație în segmente
În cazul în care numerele A, B, C, D sunt diferite de zero, forma ecuației (0) poate fi după cum urmează:
x/a + y/b + z/c = 1,
în care a = -D/A, b = -D/B, c = -D/C.
Ca rezultat, este de remarcat faptul că acest plan va intersecta axa Ox într-un punct cu coordonatele (a,0,0), Oy - (0,b,0) și Oz - (0,0,c). ).

Ținând cont de ecuația x/a + y/b + z/c = 1, nu este dificil să ne imaginăm vizual plasarea planului în raport cu un sistem de coordonate dat.
Coordonate vectoriale normale
Vectorul normal n la planul P are coordonate care sunt coeficienți ai ecuației generale a acestui plan, adică n (A, B, C).

Pentru a determina coordonatele normalei n, este suficient să cunoaștem ecuația generală a unui plan dat.
Când folosiți o ecuație în segmente, care are forma x/a + y/b + z/c = 1, ca și atunci când utilizați o ecuație generală, puteți scrie coordonatele oricărui vector normal al unui plan dat: (1/a + 1/b + 1/ Cu).
Este de remarcat faptul că vectorul normal ajută la rezolvarea unei varietăți de probleme. Cele mai frecvente includ probleme care presupun demonstrarea perpendicularității sau paralelismului planelor, probleme de găsire a unghiurilor între plane sau unghiurilor dintre plane și drepte.
Tip de ecuație plană în funcție de coordonatele punctului și ale vectorului normal
Un vector diferit de zero n perpendicular pe un plan dat este numit normal pentru un plan dat.
Să presupunem că în spațiul de coordonate (sistem de coordonate dreptunghiulare) Oxyz sunt date:
- punctul Mₒ cu coordonatele (xₒ,yₒ,zₒ);
- vector zero n=A*i+B*j+C*k.

Este necesar să se creeze o ecuație pentru un plan care va trece prin punctul Mₒ perpendicular pe normala n.
Alegem orice punct arbitrar din spațiu și îl notăm M (x y, z). Fie vectorul rază al oricărui punct M (x,y,z) r=x*i+y*j+z*k, iar vectorul rază al punctului Mₒ (xₒ,yₒ,zₒ) - rₒ=xₒ* i+yₒ *j+zₒ*k. Punctul M va aparține unui plan dat dacă vectorul MₒM este perpendicular pe vectorul n. Să scriem condiția de ortogonalitate folosind produsul scalar:
[MₒM, n] = 0.
Deoarece MₒM = r-rₒ, ecuația vectorială a planului va arăta astfel:
Această ecuație poate avea altă formă. Pentru a face acest lucru, se folosesc proprietățile produsului scalar, iar partea stângă a ecuației este transformată. = - . Dacă îl notăm c, obținem următoarea ecuație: - c = 0 sau = c, care exprimă constanța proiecțiilor pe vectorul normal al vectorilor cu rază ai punctelor date care aparțin planului.
Acum putem obține forma de coordonate de scriere a ecuației vectoriale a planului nostru = 0. Deoarece r-rₒ = (x-xₒ)*i + (y-yₒ)*j + (z-zₒ)*k și n = A*i+B *j+С*k, avem:
Rezultă că avem o ecuație pentru un plan care trece printr-un punct perpendicular pe normala n:
A*(x-xₒ)+B*(y-yₒ)C*(z-zₒ)=0.
Tip de ecuație plană în funcție de coordonatele a două puncte și un vector coliniar cu planul
Să specificăm două puncte arbitrare M′ (x′,y′,z′) și M″ (x″,y″,z″), precum și un vector a (a′,a″,a‴).
Acum putem crea o ecuație pentru un plan dat care va trece prin punctele existente M′ și M″, precum și orice punct M cu coordonatele (x, y, z) paralele cu vectorul dat a.
În acest caz, vectorii M′M=(x-x′;y-y′;z-z′) și M″M=(x″-x′;y″-y′;z″-z′) trebuie să fie coplanari cu vectorul a=(a′,a″,a‴), ceea ce înseamnă că (M′M, M″M, a)=0.
Deci, ecuația noastră plană din spațiu va arăta astfel:

Tip de ecuație a unui plan care intersectează trei puncte
Să presupunem că avem trei puncte: (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴), care nu aparțin aceleiași drepte. Este necesar să scrieți ecuația unui plan care trece prin trei puncte date. Teoria geometriei susține că acest tip de plan există cu adevărat, dar este singurul și unic. Deoarece acest plan intersectează punctul (x′,y′,z′), forma ecuației sale va fi după cum urmează:
Aici A, B, C sunt diferite de zero în același timp. De asemenea, planul dat intersectează încă două puncte: (x″,y″,z″) și (x‴,y‴,z‴). În acest sens, trebuie îndeplinite următoarele condiții:

Acum putem crea un sistem omogen cu necunoscute u, v, w:

În cazul nostru, x, y sau z este un punct arbitrar care satisface ecuația (1). Având în vedere ecuația (1) și sistemul de ecuații (2) și (3), sistemul de ecuații indicat în figura de mai sus este satisfăcut de vectorul N (A,B,C), care este netrivial. De aceea determinantul acestui sistem este egal cu zero.

Ecuația (1) pe care am obținut-o este ecuația planului. Trece prin 3 puncte exact, iar acest lucru este ușor de verificat. Pentru a face acest lucru, trebuie să ne extindem determinantul în elementele din primul rând. Din proprietățile existente ale determinantului rezultă că planul nostru intersectează simultan trei puncte date inițial (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴) . Adică am rezolvat sarcina care ne-a fost atribuită.
Unghiul diedric dintre plane
Un unghi diedru este o figură geometrică spațială formată din două semiplane care emană dintr-o linie dreaptă. Cu alte cuvinte, aceasta este partea din spațiu care este limitată de aceste semiplanuri.
Să presupunem că avem două plane cu următoarele ecuații:

Știm că vectorii N=(A,B,C) și N¹=(A¹,B¹,C¹) sunt perpendiculari conform planurilor date. În acest sens, unghiul φ dintre vectorii N și N¹ este egal cu unghiul (diedrul) care se află între aceste plane. Produsul punctual are forma:
NN¹=|N||N¹|cos φ,
tocmai pentru că
cosφ= NN¹/|N||N¹|=(AA¹+BB¹+CC¹)/((√(A²+B²+C²))*(√(A¹)²+(B¹)²+(C¹)²)).

Este suficient să ținem cont că 0≤φ≤π.
De fapt, două plane care se intersectează formează două unghiuri (diedre): φ 1 și φ 2. Suma lor este egală cu π (φ 1 + φ 2 = π). În ceea ce privește cosinusurile lor, valorile lor absolute sunt egale, dar diferă în semn, adică cos φ 1 = -cos φ 2. Dacă în ecuația (0) înlocuim A, B și C cu numerele -A, -B și respectiv -C, atunci ecuația pe care o obținem va determina același plan, singurul, unghiul φ din ecuația cos φ= NN 1 /| N||N 1 | va fi înlocuit cu π-φ.
Ecuația unui plan perpendicular
Planurile între care unghiul este de 90 de grade se numesc perpendiculare. Folosind materialul prezentat mai sus, putem găsi ecuația unui plan perpendicular pe altul. Să presupunem că avem două plane: Ax+By+Cz+D=0 și A¹x+B¹y+C¹z+D=0. Putem spune că vor fi perpendiculare dacă cosφ=0. Aceasta înseamnă că NN¹=AA¹+BB¹+CC¹=0.
Ecuația planului paralel
Două plane care nu conțin puncte comune se numesc paralele.
Condiția (ecuațiile lor sunt aceleași ca în paragraful anterior) este ca vectorii N și N¹, care sunt perpendiculari pe ei, să fie coliniari. Aceasta înseamnă că sunt îndeplinite următoarele condiții de proporționalitate:
A/A¹=B/B¹=C/C1.
Dacă condițiile de proporționalitate sunt extinse - A/A¹=B/B¹=C/C¹=DD¹,
aceasta indică faptul că aceste planuri coincid. Aceasta înseamnă că ecuațiile Ax+By+Cz+D=0 și A¹x+B¹y+C¹z+D¹=0 descriu un plan.
Distanța până la avion de la punct
Să presupunem că avem un plan P, care este dat de ecuația (0). Este necesar să găsiți distanța până la acesta de la un punct cu coordonatele (xₒ,yₒ,zₒ)=Qₒ. Pentru a face acest lucru, trebuie să aduceți ecuația planului P în formă normală:
(ρ,v)=р (р≥0).
În acest caz, ρ (x,y,z) este vectorul rază a punctului nostru Q situat pe P, p este lungimea perpendicularei P care a fost eliberată din punctul zero, v este vectorul unitar, care este situat în direcția a.
Diferența ρ-ρº vector de rază a unui punct Q = (x, y, z), aparținând lui P, precum și vectorul de rază a unui punct dat Q 0 = (xₒ, уₒ, zₒ) este un astfel de vector, valoarea absolută a proiecției căreia pe v este egală cu distanța d care trebuie găsită de la Q 0 = (xₒ,уₒ,zₒ) la P:
D=|(ρ-ρ 0 ,v)|, dar
(ρ-ρ 0 ,v)= (ρ,v)-(ρ 0 ,v) =р-(ρ 0 ,v).
Deci se dovedește
d=|(ρ 0 ,v)-р|.
Astfel, vom găsi valoarea absolută a expresiei rezultate, adică d dorită.
Folosind limbajul parametrilor, obținem ceea ce este evident:
d=|Ахₒ+Вуₒ+Czₒ|/√(А²+В²+С²).
Dacă un punct dat Q 0 este de cealaltă parte a planului P, ca originea coordonatelor, atunci între vectorul ρ-ρ 0 și v există deci:
d=-(ρ-ρ 0 ,v)=(ρ 0 ,v)-р>0.
În cazul în care punctul Q 0, împreună cu originea coordonatelor, este situat pe aceeași parte a lui P, atunci unghiul creat este ascuțit, adică:
d=(ρ-ρ 0 ,v)=р - (ρ 0 , v)>0.
Ca urmare, rezultă că în primul caz (ρ 0 ,v)>р, în al doilea (ρ 0 ,v)<р.
Planul tangent și ecuația acestuia
Planul tangent la suprafață în punctul de contact Mº este un plan care conține toate tangentele posibile la curbele trasate prin acest punct de pe suprafață.
Cu acest tip de ecuație de suprafață F(x,y,z)=0, ecuația planului tangent la punctul tangent Mº(xº,yº,zº) va arăta astfel:
F x (xº,yº,zº)(x- xº)+ F x (xº, yº, zº)(y- yº)+ F x (xº, yº,zº)(z-zº)=0.
Dacă specificați suprafața în formă explicită z=f (x,y), atunci planul tangent va fi descris de ecuația:
z-zº =f(xº, yº)(x- xº)+f(xº, yº)(y- yº).
Intersecția a două planuri
În sistemul de coordonate (dreptunghiular) se află Oxyz, sunt date două plane П′ și П″, care se intersectează și nu coincid. Deoarece orice plan situat într-un sistem de coordonate dreptunghiular este determinat de o ecuație generală, vom presupune că P′ și P″ sunt date de ecuațiile A′x+B′y+C′z+D′=0 și A″x +B″y+ С″z+D″=0. În acest caz, avem normala n′ (A′,B′,C′) a planului P′ și normala n″ (A″,B″,C″) a planului P″. Deoarece planurile noastre nu sunt paralele și nu coincid, acești vectori nu sunt coliniari. Folosind limbajul matematicii, putem scrie această condiție astfel: n′≠ n″ ↔ (A′,B′,C′) ≠ (λ*A″,λ*B″,λ*C″), λϵR. Fie ca linia dreaptă care se află la intersecția dintre P′ și P″ se notează cu litera a, în acest caz a = P′ ∩ P″.
a este o linie dreaptă constând din mulțimea tuturor punctelor planurilor (comune) P′ și P″. Aceasta înseamnă că coordonatele oricărui punct aparținând dreptei a trebuie să satisfacă simultan ecuațiile A′x+B′y+C′z+D′=0 și A″x+B″y+C″z+D″=0 . Aceasta înseamnă că coordonatele punctului vor fi o soluție parțială a următorului sistem de ecuații:

Ca urmare, se dovedește că soluția (generală) a acestui sistem de ecuații va determina coordonatele fiecăruia dintre punctele dreptei, care va acționa ca punct de intersecție al lui P′ și P″, și va determina linia dreaptă a în sistemul de coordonate Oxyz (dreptunghiular) în spațiu.
Pentru a obține ecuația generală a unui plan, să analizăm planul care trece printr-un punct dat.
Să existe trei axe de coordonate deja cunoscute de noi în spațiu - Bou, OiȘi Oz. Țineți foaia de hârtie astfel încât să rămână plată. Avionul va fi foaia în sine și continuarea ei în toate direcțiile.
Lăsa P plan arbitrar în spațiu. Fiecare vector perpendicular pe acesta se numește vector normal la acest avion. Desigur, vorbim despre un vector diferit de zero.
Dacă se cunoaşte vreun punct al avionului Pși un vector normal al acestuia, atunci prin aceste două condiții planul în spațiu este complet definit(printr-un punct dat puteți desena un singur plan perpendicular pe vectorul dat). Ecuația generală a planului va fi:
![]()
Deci, condițiile care definesc ecuația planului sunt. Pentru a te obține ecuația plană, având forma de mai sus, ia în avion P arbitrar punct M cu coordonate variabile X, y, z. Acest punct aparține planului numai dacă vector perpendicular pe vector(Fig. 1). Pentru aceasta, conform condiției de perpendicularitate a vectorilor, este necesar și suficient ca produsul scalar al acestor vectori să fie egal cu zero, adică
Vectorul este specificat de condiție. Găsim coordonatele vectorului folosind formula ![]() :
:
![]() .
.
Acum, folosind formula produsului scalar al vectorilor ![]() , exprimăm produsul scalar sub formă de coordonate:
, exprimăm produsul scalar sub formă de coordonate:
De la punctul M(x; y; z) este aleasă arbitrar pe plan, apoi ultima ecuație este satisfăcută de coordonatele oricărui punct situat pe plan P. Pentru un punct N, neîntins într-un anumit plan, adică egalitatea (1) este încălcată.
Exemplul 1. Scrieți o ecuație pentru un plan care trece printr-un punct și perpendicular pe vector.
Soluţie. Să folosim formula (1) și să ne uităm din nou:
În această formulă numerele A , BȘi C coordonate vectoriale și numere X0 , y0 Și z0 - coordonatele punctului.
Calculele sunt foarte simple: înlocuim aceste numere în formulă și obținem
Înmulțim tot ce trebuie înmulțit și adunăm doar numere (care nu au litere). Rezultat:
![]() .
.
Ecuația necesară a planului din acest exemplu s-a dovedit a fi exprimată printr-o ecuație generală de gradul întâi în raport cu coordonatele variabile x, y, z punct arbitrar al planului.
Deci, o ecuație a formei
numit ecuația planului general .
Exemplul 2. Construiți într-un sistem de coordonate carteziene dreptunghiulare un plan dat de ecuație ![]() .
.
Soluţie. Pentru a construi un plan, este necesar și suficient să cunoașteți oricare trei dintre punctele sale care nu se află pe aceeași linie dreaptă, de exemplu, punctele de intersecție ale planului cu axele de coordonate.
Cum să găsești aceste puncte? Pentru a găsi punctul de intersecție cu axa Oz, trebuie să înlocuiți zerourile pentru X și Y în ecuația dată în enunțul problemei: X = y= 0 . Prin urmare primim z= 6. Astfel, planul dat intersectează axa Oz la punct A(0; 0; 6) .
În același mod găsim punctul de intersecție al planului cu axa Oi. La X = z= 0 obținem y= −3, adică punctul B(0; −3; 0) .
Și, în sfârșit, găsim punctul de intersecție al planului nostru cu axa Bou. La y = z= 0 obținem X= 2, adică un punct C(2; 0; 0). Pe baza celor trei puncte obținute în soluția noastră A(0; 0; 6) , B(0; −3; 0) și C(2; 0; 0) construiți planul dat.
Să luăm în considerare acum cazuri speciale ale ecuaţiei planului general. Acestea sunt cazurile în care anumiți coeficienți ai ecuației (2) devin zero.
1. Când D= 0 ecuație ![]() definește un plan care trece prin origine, deoarece coordonatele punctului 0
(0; 0; 0) satisface această ecuație.
definește un plan care trece prin origine, deoarece coordonatele punctului 0
(0; 0; 0) satisface această ecuație.
2. Când A= 0 ecuație ![]() definește un plan paralel cu axa Bou, deoarece vectorul normal al acestui plan este perpendicular pe axa Bou(proiecția sa pe axă Bou egal cu zero). La fel, când B= 0 avion
definește un plan paralel cu axa Bou, deoarece vectorul normal al acestui plan este perpendicular pe axa Bou(proiecția sa pe axă Bou egal cu zero). La fel, când B= 0 avion ![]() paralel cu axa Oi, și atunci când C= 0 avion
paralel cu axa Oi, și atunci când C= 0 avion ![]() paralel cu axa Oz.
paralel cu axa Oz.
3. Când A=D= Ecuația 0 definește un plan care trece prin axă Bou, deoarece este paralelă cu axa Bou (A=D= 0). În mod similar, planul trece prin axă Oi, iar planul prin axă Oz.
4. Când A=B= Ecuația 0 definește un plan paralel cu planul de coordonate xOy, deoarece este paralel cu axele Bou (A= 0) și Oi (B= 0). În mod similar, planul este paralel cu planul yOz, iar avionul este avionul xOz.
5. Când A=B=D= 0 ecuație (sau z = 0) definește planul de coordonate xOy, deoarece este paralel cu planul xOy (A=B= 0) și trece prin origine ( D= 0). La fel, Eq. y = 0 în spațiu definește planul de coordonate xOz, și ecuația x = 0 - plan de coordonate yOz.
Exemplul 3. Creați o ecuație a planului P, trecând prin axă Oiși punct.
Soluţie. Deci planul trece prin axă Oi. Prin urmare, în ecuația ei y= 0 și această ecuație are forma . Pentru a determina coeficienții AȘi C să profităm de faptul că punctul aparține planului P .
Prin urmare, printre coordonatele sale se numără cele care pot fi substituite în ecuația plană pe care am derivat-o deja (). Să ne uităm din nou la coordonatele punctului:
M0 (2; −4; 3) .
Printre ei X = 2 , z= 3 . Le substituim în ecuația generală și obținem ecuația pentru cazul nostru particular:
2A + 3C = 0 .
Lasă 2 Aîn partea stângă a ecuației, mutați 3 Cîn partea dreaptă și ajungem
A = −1,5C .
Înlocuirea valorii găsite Aîn ecuație, obținem
![]() sau .
sau .
Aceasta este ecuația necesară în condiția exemplu.
Rezolvați singur problema ecuației plane și apoi uitați-vă la soluție
Exemplul 4. Definiți un plan (sau planuri, dacă mai multe) în raport cu axele de coordonate sau planurile de coordonate dacă planul (planurile) este dat de ecuație.
Soluțiile la problemele tipice care apar în timpul testelor sunt în manualul „Probleme pe un plan: paralelism, perpendicularitate, intersecția a trei plane într-un punct”.
Ecuația unui plan care trece prin trei puncte
După cum sa menționat deja, o condiție necesară și suficientă pentru construirea unui plan, pe lângă un punct și vectorul normal, sunt și trei puncte care nu se află pe aceeași dreaptă.
Să fie date trei puncte diferite , și , care nu se află pe aceeași linie. Deoarece cele trei puncte indicate nu se află pe aceeași dreaptă, vectorii nu sunt coliniari și, prin urmare, orice punct din plan se află în același plan cu punctele și dacă și numai dacă vectorii și ![]() coplanare, adică atunci și numai când produsul mixt al acestor vectori este egal cu zero.
coplanare, adică atunci și numai când produsul mixt al acestor vectori este egal cu zero.
Folosind expresia produsului mixt în coordonate, obținem ecuația planului
 (3)
(3)
După dezvăluirea determinantului, această ecuație devine o ecuație de forma (2), adică. ecuația generală a planului.
Exemplul 5. Scrieți o ecuație pentru un plan care trece prin trei puncte date care nu se află pe aceeași dreaptă:
și determinați un caz special al ecuației generale a unei drepte, dacă există.
Soluţie. Conform formulei (3) avem:

Ecuație plană normală. Distanța de la punct la plan
Ecuația normală a unui plan este ecuația acestuia, scrisă sub forma