Opera de artă vectorială este un pseudovector perpendicular pe un plan construit din doi factori, care este rezultatul operației binare „înmulțire vectorială” peste vectori din spațiul euclidian tridimensional. Produsul vectorial nu are proprietățile comutativității și asociativității (este anticomutativ) și, spre deosebire de produsul scalar al vectorilor, este un vector. Utilizat pe scară largă în multe aplicații de inginerie și fizică. De exemplu, momentul unghiular și forța Lorentz sunt scrise matematic ca produs vectorial. Produsul încrucișat este util pentru „măsurarea” perpendicularității vectorilor - modulul produsului încrucișat a doi vectori este egal cu produsul modulelor lor dacă aceștia sunt perpendiculari și scade la zero dacă vectorii sunt paraleli sau antiparaleli.
Produsul vectorial poate fi definit în diferite moduri și, teoretic, într-un spațiu de orice dimensiune n, se poate calcula produsul n-1 vectori, obținând astfel un singur vector perpendicular pe toți. Dar dacă produsul este limitat la produse binare non-triviale cu rezultate vectoriale, atunci produsul vectorial tradițional este definit doar în spații tridimensionale și șapte-dimensionale. Rezultatul unui produs vectorial, ca un produs scalar, depinde de metrica spațiului euclidian.
Spre deosebire de formula pentru calcularea vectorilor de produs scalar din coordonatele unui sistem de coordonate dreptunghiular tridimensional, formula produsului încrucișat depinde de orientarea sistemului de coordonate dreptunghiulare sau, cu alte cuvinte, de „chiralitatea” acestuia.
Definiție:
Produsul vectorial al vectorului a și al vectorului b în spațiul R3 este un vector c care îndeplinește următoarele cerințe:
lungimea vectorului c este egală cu produsul dintre lungimile vectorilor a și b și sinusul unghiului φ dintre ei:
|c|=|a||b|sin φ;
vectorul c este ortogonal cu fiecare dintre vectorii a și b;
vectorul c este direcționat astfel încât triplul vectorilor abc să fie dreptaci;
în cazul spaţiului R7 se cere asociativitatea triplului vectorilor a, b, c.
Desemnare:
c===a × b
Orez. 1. Aria unui paralelogram este egală cu modulul produsului vectorial
Proprietățile geometrice ale unui produs încrucișat:
O condiție necesară și suficientă pentru coliniaritatea a doi vectori nenuli este ca produsul lor vectorial să fie egal cu zero.
Modul încrucișat de produse egal cu suprafata S paralelogram construit pe vectori reduși la o origine comună AȘi b(vezi fig. 1).
Dacă e- vector unitar ortogonal cu vectorii AȘi bşi ales astfel încât trei a fi- corect, și S este aria paralelogramului construit pe ele (redusă la o origine comună), atunci formula pentru produsul vectorial este valabilă:
=S e
Fig.2. Volumul unui paralelipiped folosind vectorul și produsul scalar al vectorilor; liniile punctate arată proiecțiile vectorului c pe a × b și ale vectorului a pe b × c, primul pas este găsirea produselor scalare
Dacă c- un vector, π
- orice plan care conține acest vector, e- vector unitar situat în plan π
și ortogonală la c,g- vector unitar ortogonal cu planul π
şi direcţionată astfel încât triplul vectorilor ecg este corect, atunci pentru orice culcat în avion π
vector A formula este corecta:
=Pr e a |c|g
unde Pr e a este proiecția vectorului e pe a
|c|-modul vectorului c
Când utilizați produse vectoriale și scalare, puteți calcula volumul unui paralelipiped construit pe vectori reduși la o origine comună a, bȘi c. Un astfel de produs de trei vectori se numește mixt.
V=|a (b×c)|
Figura arată că acest volum poate fi găsit în două moduri: rezultatul geometric este păstrat chiar și atunci când produsele „scalare” și „vectorale” sunt schimbate:
V=a×b c=a b×c
Mărimea produsului încrucișat depinde de sinusul unghiului dintre vectorii originali, astfel încât produsul încrucișat poate fi perceput ca gradul de „perpendicularitate” al vectorilor, la fel cum produsul scalar poate fi văzut ca gradul de „paralelism”. ”. Produsul vectorial al doi vectori unitari este egal cu 1 (vector unitar) daca vectorii originali sunt perpendiculari si egal cu 0 (vector zero) daca vectorii sunt paraleli sau antiparaleli.
Exprimarea produsului încrucișat în coordonate carteziene
Dacă doi vectori AȘi b definite prin coordonatele lor carteziene dreptunghiulare sau, mai precis, reprezentate pe o bază ortonormală
a=(a x ,a y ,a z)
b=(b x ,b y ,b z)
iar sistemul de coordonate este dreptaci, atunci produsul lor vectorial are forma
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Pentru a reține această formulă:
i =∑ε ijk a j b k
Unde ε ijk- simbolul lui Levi-Civita.
Unghiul dintre vectori
Pentru a introduce conceptul de produs vectorial al doi vectori, trebuie mai întâi să înțelegem un astfel de concept ca unghiul dintre acești vectori.
Să ne dăm doi vectori $\overline(α)$ și $\overline(β)$. Să luăm un punct $O$ din spațiu și să trasăm vectorii $\overline(α)=\overline(OA)$ și $\overline(β)=\overline(OB)$ din acesta, apoi unghiul $AOB$ se va numi unghiul dintre acești vectori (Fig. 1).
Notație: $∠(\overline(α),\overline(β))$
Conceptul de produs vectorial al vectorilor și formula de găsire
Definiția 1
Produsul vectorial al doi vectori este un vector perpendicular pe ambii vectori dați, iar lungimea lui va fi egală cu produsul lungimilor acestor vectori cu sinusul unghiului dintre acești vectori și, de asemenea, acest vector cu doi inițiali are aceeași orientare ca și sistemul de coordonate carteziene.
Notație: $\overline(α)х\overline(β)$.
Matematic arata cam asa:
- $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin∠(\overline(α),\overline(β))$
- $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
- $(\overline(α)х\overline(β),\overline(α),\overline(β))$ și $(\overline(i),\overline(j),\overline(k))$ sunt aceeași orientată (Fig. 2)
Evident, produsul exterior al vectorilor va fi egal cu vectorul zero în două cazuri:
- Dacă lungimea unuia sau a ambilor vectori este zero.
- Dacă unghiul dintre acești vectori este egal cu $180^\circ$ sau $0^\circ$ (deoarece în acest caz sinusul este zero).
Pentru a vedea clar cum se găsește produsul vectorial al vectorilor, luați în considerare următoarele exemple de soluții.
Exemplul 1
Aflați lungimea vectorului $\overline(δ)$, care va fi rezultatul produsului vectorial al vectorilor, cu coordonatele $\overline(α)=(0,4,0)$ și $\overline(β) =(3,0,0 )$.
Soluţie.
Să descriem acești vectori în spațiul de coordonate carteziene (Fig. 3):
Figura 3. Vectorii în spațiul de coordonate carteziene. Autor24 - schimb online de lucrări ale studenților
Vedem că acești vectori se află pe axele $Ox$ și, respectiv, $Oy$. Prin urmare, unghiul dintre ele va fi $90^\circ$. Să aflăm lungimile acestor vectori:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
Apoi, prin Definiția 1, obținem modulul $|\overline(δ)|$
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
Răspuns: $12$.
Calcularea produsului încrucișat din coordonatele vectoriale
Definiția 1 implică imediat o metodă pentru găsirea produsului vectorial pentru doi vectori. Deoarece un vector, pe lângă valoarea sa, are și o direcție, este imposibil să-l găsim doar folosind o mărime scalară. Dar, pe lângă aceasta, există și o modalitate de a găsi vectorii pe care ni le-au dat folosind coordonatele.
Să ni se dea vectorii $\overline(α)$ și $\overline(β)$, care vor avea coordonatele $(α_1,α_2,α_3)$ și, respectiv, $(β_1,β_2,β_3)$. Apoi vectorul produsului încrucișat (și anume coordonatele sale) poate fi găsit folosind următoarea formulă:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
În caz contrar, extinzând determinantul, obținem următoarele coordonate
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Exemplul 2
Găsiți vectorul produsului vectorial al vectorilor coliniari $\overline(α)$ și $\overline(β)$ cu coordonatele $(0,3,3)$ și $(-1,2,6)$.
Soluţie.
Să folosim formula dată mai sus. Primim
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$
Răspuns: $(12,-3,3)$.
Proprietăți ale produsului vectorial al vectorilor
Pentru trei vectori amestecați arbitrar $\overline(α)$, $\overline(β)$ și $\overline(γ)$, precum și $r∈R$, sunt valabile următoarele proprietăți:
Exemplul 3
Găsiți aria unui paralelogram ale cărui vârfuri au coordonatele $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ și $(3,8,0) $.
Soluţie.
Mai întâi, să descriem acest paralelogram în spațiul de coordonate (Fig. 5):
Figura 5. Paralelogram în spațiul de coordonate. Autor24 - schimb online de lucrări ale studenților
Vedem că cele două laturi ale acestui paralelogram sunt construite folosind vectori coliniari cu coordonatele $\overline(α)=(3,0,0)$ și $\overline(β)=(0,8,0)$. Folosind a patra proprietate, obținem:
$S=|\overline(α)х\overline(β)|$
Să găsim vectorul $\overline(α)х\overline(β)$:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
Prin urmare
$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$
Evident, în cazul unui produs vectorial, contează, în plus, ordinea în care sunt luați vectorii,
De asemenea, direct din definiție rezultă că pentru orice factor scalar k (număr) este adevărat:
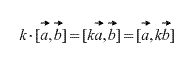
Produsul încrucișat al vectorilor coliniari este egal cu vectorul zero. Mai mult, produsul încrucișat al doi vectori este zero dacă și numai dacă aceștia sunt coliniari. (În cazul în care unul dintre ele este un vector zero, este necesar să ne amintim că un vector zero este coliniar cu orice vector prin definiție).
Produsul vectorial are proprietate distributivă, acesta este
Exprimarea produsului vectorial prin coordonatele vectorilor.
Să fie dați doi vectori
(cum să găsiți coordonatele unui vector din coordonatele începutului și sfârșitului său - consultați articolul Produsul punctual al vectorilor, articolul Definiția alternativă a produsului scalar sau calcularea produsului scalar a doi vectori specificati de coordonatele lor.)
De ce aveți nevoie de un produs vectorial?
Există multe modalități de a utiliza produsul încrucișat, de exemplu, așa cum este scris mai sus, calculând produsul încrucișat a doi vectori, puteți afla dacă aceștia sunt coliniari.
Sau poate fi folosit ca o modalitate de a calcula aria unui paralelogram construit din acești vectori. Pe baza definiției, lungimea vectorului rezultat este aria paralelogramului dat.
Există, de asemenea, un număr mare de aplicații în electricitate și magnetism.Calculator de produse vectoriale online.
Pentru a găsi produsul scalar a doi vectori folosind acest calculator, trebuie să introduceți coordonatele primului vector pe prima linie în ordine, iar al doilea pe a doua linie. Coordonatele vectorilor pot fi calculate din coordonatele începutului și sfârșitului lor (vezi articolul Produsul scalar al vectorilor, element O definiție alternativă a produsului scalar sau calcularea produsului scalar al doi vectori dat de coordonatele lor.)
În această lecție ne vom uita la alte două operații cu vectori: produs vectorial al vectorilorȘi produs mixt al vectorilor (link imediat pentru cei care au nevoie). Este în regulă, uneori se întâmplă că pentru fericire deplină, în plus produsul scalar al vectorilor, sunt necesare din ce în ce mai multe. Aceasta este dependența de vectori. Poate părea că intrăm în jungla geometriei analitice. Este gresit. În această secțiune a matematicii superioare există în general puțin lemn, cu excepția poate suficient pentru Pinocchio. De fapt, materialul este foarte comun și simplu - cu greu mai complicat decât același produs scalar, vor fi chiar mai puține sarcini tipice. Principalul lucru în geometria analitică, așa cum mulți vor fi convinși sau s-au lăsat deja convinși, este A NU FACE GREȘELI LA CALCULE. Repetă ca o vrajă și vei fi fericit =)
Dacă vectorii strălucesc undeva departe, ca fulgerul la orizont, nu contează, începe cu lecția Vectori pentru manechine pentru a restabili sau redobândi cunoștințe de bază despre vectori. Cititorii mai pregătiți se pot familiariza cu informațiile selectiv; am încercat să colectez cea mai completă colecție de exemple care se găsesc adesea în lucrările practice
Ce te va face fericit imediat? Când eram mică, puteam jongla cu două sau chiar trei bile. A mers bine. Acum nu va trebui să jonglați deloc, pentru că vom lua în considerare numai vectori spațiali, iar vectorii plati cu două coordonate vor fi lăsați afară. De ce? Așa s-au născut aceste acțiuni - vectorul și produsul mixt al vectorilor sunt definite și funcționează în spațiul tridimensional. Deja este mai ușor!
Această operație, la fel ca și produsul scalar, implică doi vectori. Să fie acestea litere nepieritoare.
Acțiunea în sine notat cuîn felul următor: . Există și alte opțiuni, dar sunt obișnuit să notez produsul vectorial al vectorilor în acest fel, între paranteze pătrate cu o cruce.
Și imediat întrebare: dacă în produsul scalar al vectorilor sunt implicați doi vectori și aici se înmulțesc și doi vectori, atunci Care este diferența? Diferența evidentă este, în primul rând, în REZULTAT:
Rezultatul produsului scalar al vectorilor este NUMĂR:
Rezultatul produsului încrucișat al vectorilor este VECTOR: , adică înmulțim vectorii și obținem din nou un vector. Club închis. De fapt, de aici provine numele operațiunii. În diferite literaturi educaționale, desemnările pot varia și ele; voi folosi litera.
Definiţia cross product
Mai întâi va fi o definiție cu o imagine, apoi comentarii.
Definiție: produs vectorial necoliniare vectori, luate în această ordine, numit VECTOR, lungime care este numeric egală cu aria paralelogramului, construit pe acești vectori; vector ortogonală la vectori, și este îndreptată astfel încât baza să aibă o orientare corectă: 
Să dezvăluim definiția, sunt o mulțime de lucruri interesante aici!
Astfel, se pot evidenția următoarele puncte semnificative:
1) Vectorii originali, indicați prin săgeți roșii, prin definiție nu coliniare. Va fi potrivit să luăm în considerare cazul vectorilor coliniari puțin mai târziu.
2) Se iau vectori într-o ordine strict definită: – „a” se înmulțește cu „fi”, nu „fi” cu „a”. Rezultatul înmulțirii vectoriale este VECTOR, care este indicat cu albastru. Dacă vectorii sunt înmulțiți în ordine inversă, obținem un vector egal ca lungime și opus ca direcție (culoarea zmeurului). Adică, egalitatea este adevărată 
.
3) Acum să ne familiarizăm cu semnificația geometrică a produsului vectorial. Acesta este un punct foarte important! LUNGIMEA vectorului albastru (și, prin urmare, a vectorului purpuriu) este numeric egală cu AREA paralelogramului construit pe vectori. În figură, acest paralelogram este umbrit în negru.
Notă : desenul este schematic și, desigur, lungimea nominală a produsului vectorial nu este egală cu aria paralelogramului.
Să ne amintim una dintre formulele geometrice: Aria unui paralelogram este egală cu produsul laturilor adiacente și sinusul unghiului dintre ele. Prin urmare, pe baza celor de mai sus, formula de calcul a LUNGIMEI unui produs vectorial este valabilă:
Subliniez că formula este despre LUNGIMEA vectorului și nu despre vectorul în sine. Care este sensul practic? Și semnificația este că în problemele de geometrie analitică, aria unui paralelogram este adesea găsită prin conceptul de produs vectorial:
Să obținem a doua formulă importantă. Diagonala unui paralelogram (linie punctată roșie) îl împarte în două triunghiuri egale. Prin urmare, aria unui triunghi construit pe vectori (umbrire roșie) poate fi găsită folosind formula:
4) Un fapt la fel de important este că vectorul este ortogonal cu vectorii, adică 
. Desigur, vectorul direcționat opus (săgeata zmeură) este, de asemenea, ortogonal cu vectorii originali.
5) Vectorul este îndreptat astfel încât bază Are dreapta orientare. În lecția despre trecerea la o nouă bază Am vorbit suficient de detaliat despre orientarea planului, iar acum ne vom da seama ce este orientarea în spațiu. Îți voi explica pe degete mana dreapta. Combinați mental degetul arătător cu vector şi degetul mijlociu cu vector. Degetul inelar și degetul mic apăsați-l în palmă. Ca urmare deget mare– produsul vectorial va căuta în sus. Aceasta este o bază orientată spre dreapta (este cea din figură). Acum schimbați vectorii ( degetele arătător și mijlociu) în unele locuri, ca rezultat, degetul mare se va întoarce, iar produsul vectorial va privi deja în jos. Aceasta este, de asemenea, o bază orientată spre dreapta. S-ar putea să aveți o întrebare: ce bază a lăsat orientarea? „Atribuiți” acelorași degete mâna stângă vectori și obțineți baza stângă și orientarea la stânga a spațiului (în acest caz, degetul mare va fi situat în direcția vectorului inferior). Figurat vorbind, aceste baze „întorc” sau orientează spațiul în direcții diferite. Și acest concept nu ar trebui considerat ceva exagerat sau abstract - de exemplu, orientarea spațiului este schimbată de cea mai obișnuită oglindă, iar dacă „trageți obiectul reflectat din oglindă”, atunci în cazul general nu va fi posibil să-l combinați cu „originalul”. Apropo, ține trei degete de oglindă și analizează reflexia ;-)
...ce bine e despre care știi acum orientat spre dreapta și spre stânga baze, deoarece afirmațiile unor lectori despre o schimbare de orientare sunt înfricoșătoare =)
Produsul încrucișat al vectorilor coliniari
Definiția a fost discutată în detaliu, rămâne să aflăm ce se întâmplă când vectorii sunt coliniari. Dacă vectorii sunt coliniari, atunci ei pot fi plasați pe o linie dreaptă și paralelogramul nostru se „pliază” într-o singură linie dreaptă. Zona de astfel de, așa cum spun matematicienii, degenerat paralelogramul este egal cu zero. Același lucru rezultă din formula - sinusul lui zero sau 180 de grade este egal cu zero, ceea ce înseamnă că aria este zero
Astfel, dacă , atunci 
Și 
. Vă rugăm să rețineți că produsul vectorial în sine este egal cu vectorul zero, dar în practică acest lucru este adesea neglijat și se scrie că este, de asemenea, egal cu zero.
Un caz special este produsul încrucișat al unui vector cu el însuși:
Folosind produsul vectorial, puteți verifica coliniaritatea vectorilor tridimensionali și vom analiza și această problemă, printre altele.
Pentru a rezolva exemple practice este posibil să aveți nevoie tabel trigonometric pentru a găsi valorile sinusurilor din ea.
Ei bine, hai să aprindem focul:
Exemplul 1
a) Aflați lungimea produsului vectorial al vectorilor dacă 
b) Aflați aria unui paralelogram construit pe vectori dacă 
Soluţie: Nu, aceasta nu este o greșeală de tipar, am făcut în mod deliberat datele inițiale din clauze la fel. Pentru că designul soluțiilor va fi diferit!
a) În funcție de condiție, trebuie să găsiți lungime vector (produs încrucișat). Conform formulei corespunzătoare:
Răspuns:
Dacă ați fost întrebat despre lungime, atunci în răspuns indicăm dimensiunea - unități.
b) În funcție de condiție, trebuie să găsiți pătrat paralelogram construit pe vectori. Aria acestui paralelogram este numeric egală cu lungimea produsului vectorial:
Răspuns:
Vă rugăm să rețineți că răspunsul nu vorbește deloc despre produsul vectorial; am fost întrebați despre zona figurii, în consecință, dimensiunea este unități pătrate.
Ne uităm mereu la CE trebuie să găsim în funcție de condiție și, pe baza acesteia, formulăm clar Răspuns. Poate părea literalism, dar există o mulțime de literaliști printre profesori, iar misiunea are șanse mari să fie returnată pentru revizuire. Deși aceasta nu este o dispută deosebit de exagerată - dacă răspunsul este incorect, atunci se are impresia că persoana nu înțelege lucruri simple și/sau nu a înțeles esența sarcinii. Acest punct trebuie ținut întotdeauna sub control atunci când rezolvăm orice problemă la matematică superioară, dar și la alte materii.
Unde a ajuns litera mare „en”? În principiu, ar fi putut fi atașat suplimentar la soluție, dar pentru a scurta intrarea, nu am făcut asta. Sper că toată lumea înțelege asta și este o desemnare pentru același lucru.
Un exemplu popular pentru o soluție de bricolaj:
Exemplul 2
Găsiți aria unui triunghi construit pe vectori dacă 
Formula pentru găsirea ariei unui triunghi prin produsul vectorial este dată în comentariile la definiție. Soluția și răspunsul sunt la sfârșitul lecției.
În practică, sarcina este într-adevăr foarte comună; triunghiurile te pot chinui în general.
Pentru a rezolva alte probleme vom avea nevoie de:
Proprietăți ale produsului vectorial al vectorilor
Am luat în considerare deja unele proprietăți ale produsului vectorial, totuși, le voi include în această listă.
Pentru vectorii arbitrari și un număr arbitrar, următoarele proprietăți sunt adevărate:
1) În alte surse de informații, acest articol nu este de obicei evidențiat în proprietăți, dar este foarte important din punct de vedere practic. Asa ca lasa sa fie.
2) 
– mai sus se discută și proprietatea, uneori se numește anticomutativitatea. Cu alte cuvinte, ordinea vectorilor contează.
3) – asociativ sau asociativ legile produselor vectoriale. Constantele pot fi mutate cu ușurință în afara produsului vectorial. Serios, ce ar trebui să facă acolo?
4) – distribuție sau distributiv legile produselor vectoriale. Nici cu deschiderea consolelor nu sunt probleme.
Pentru a demonstra, să ne uităm la un exemplu scurt:
Exemplul 3
Găsiți dacă 
Soluţie: Condiția necesită din nou găsirea lungimii produsului vectorial. Să ne pictăm miniatura: 
(1) Conform legilor asociative, luăm constantele în afara domeniului produsului vectorial.
(2) Luăm constanta în afara modulului, iar modulul „mâncă” semnul minus. Lungimea nu poate fi negativă.
(3) Restul este clar.
Răspuns: 
Este timpul să adăugați mai multă lemne la foc:
Exemplul 4
Calculați aria unui triunghi construit pe vectori dacă 
Soluţie: Găsiți aria triunghiului folosind formula 
. Problema este că vectorii „tse” și „de” sunt ei înșiși prezentați ca sume de vectori. Algoritmul de aici este standard și amintește oarecum de exemplele nr. 3 și 4 ale lecției Produsul punctual al vectorilor. Pentru claritate, vom împărți soluția în trei etape:
1) La primul pas, exprimăm produsul vectorial prin produsul vectorial, de fapt, să exprimăm un vector în termeni de vector. Încă nu se vorbește despre lungimi!
(1) Înlocuiți expresiile vectorilor.
(2) Folosind legi distributive, deschidem parantezele după regula înmulțirii polinoamelor.
(3) Folosind legile asociative, mutăm toate constantele dincolo de produsele vectoriale. Cu puțină experiență, pașii 2 și 3 pot fi executați simultan.
(4) Primul și ultimul termen sunt egali cu zero (vector zero) datorită proprietății frumoase. În al doilea termen folosim proprietatea de anticomutativitate a unui produs vectorial:
(5) Prezentăm termeni similari.
Ca rezultat, vectorul sa dovedit a fi exprimat printr-un vector, care este ceea ce trebuia să fie realizat: 
2) În a doua etapă, găsim lungimea produsului vectorial de care avem nevoie. Această acțiune este similară cu Exemplul 3: 
3) Găsiți aria triunghiului necesar: 
Etapele 2-3 ale soluției ar fi putut fi scrise într-un singur rând.
Răspuns:
Problema luată în considerare este destul de comună în teste, iată un exemplu pentru a o rezolva singur:
Exemplul 5
Găsiți dacă
O scurtă soluție și răspuns la sfârșitul lecției. Să vedem cât de atent ai fost când ai studiat exemplele anterioare ;-)
Produsul încrucișat al vectorilor în coordonate
, specificat pe o bază ortonormală, exprimat prin formula:
Formula este foarte simplă: în linia de sus a determinantului scriem vectorii de coordonate, în a doua și a treia linie „punem” coordonatele vectorilor și punem în ordine strictă– mai întâi coordonatele vectorului „ve”, apoi coordonatele vectorului „dublu-ve”. Dacă vectorii trebuie înmulțiți într-o ordine diferită, atunci rândurile ar trebui schimbate: 
Exemplul 10
Verificați dacă următorii vectori spațiali sunt coliniari:
A)
b) 
Soluţie: Verificarea se bazează pe una dintre afirmațiile din această lecție: dacă vectorii sunt coliniari, atunci produsul lor vectorial este egal cu zero (vector zero): 
.
a) Găsiți produsul vectorial: 
Astfel, vectorii nu sunt coliniari.
b) Găsiți produsul vectorial: 
Răspuns: a) nu este coliniar, b)
Iată, probabil, toate informațiile de bază despre produsul vectorial al vectorilor.
Această secțiune nu va fi foarte mare, deoarece există puține probleme în care se utilizează produsul mixt al vectorilor. De fapt, totul va depinde de definiție, semnificația geometrică și câteva formule de lucru.
Un produs mixt de vectori este produsul a trei vectori:
Așa că s-au aliniat ca un tren și abia așteaptă să fie identificați.
Mai întâi, din nou, o definiție și o imagine:
Definiție: Lucru mixt necoplanare vectori, luate în această ordine, numit volum paralelipiped, construit pe acești vectori, echipat cu un semn „+” dacă baza este dreapta și un semn „–” dacă baza este stângă.
Hai să facem desenul. Liniile invizibile pentru noi sunt desenate cu linii punctate: 
Să ne aprofundăm în definiție:
2) Se iau vectori într-o anumită ordine, adică rearanjarea vectorilor în produs, după cum ați putea ghici, nu are loc fără consecințe.
3) Înainte de a comenta semnificația geometrică, voi observa un fapt evident: produsul mixt al vectorilor este un NUMĂR: . În literatura educațională, designul poate fi ușor diferit; sunt obișnuit să desemnez un produs mixt cu , iar rezultatul calculelor cu litera „pe”.
A-prioriu produsul amestecat este volumul paralelipipedului, construit pe vectori (figura este desenată cu vectori roșii și linii negre). Adică, numărul este egal cu volumul unui paralelipiped dat.
Notă : Desenul este schematic.
4) Să nu ne îngrijorăm din nou cu privire la conceptul de orientare a bazei și a spațiului. Semnificația părții finale este că se poate adăuga un semn minus la volum. Cu cuvinte simple, un produs mixt poate fi negativ: .
Direct din definiție urmează formula de calcul a volumului unui paralelipiped construit pe vectori.
