Ministerul Educației Generale și Profesionale al Federației Ruse

Instituție de învățământ municipală

Gimnaziul nr 12

compoziţie

pe tema: Ecuaţii şi metode de rezolvare a acestora

Completat de: elev clasa a 10-a „A”

Krutko Evgheni

Verificat de: profesor de matematică Iskhakova Gulsum Akramovna

Tyumen 2001

Plan................................................. .................................................. ...... ................................ 1

Introducere................................................. ....... ................................................. ............. ................................ 2

Parte principală................................................ .................................................. ...... ............... 3

Concluzie................................................. .................................................. ...... ............... 25

Aplicație............................................................. .................................................. ...... ................ 26

Lista literaturii utilizate.................................................. ........... ................................. 29

Plan.

Introducere.

Referință istorică.

Ecuații. Ecuații algebrice.

a) Definiții de bază.

b) Ecuația liniară și metoda de rezolvare a acesteia.

c) Ecuaţii pătratice şi metode de rezolvare a acestora.

d) Ecuații binomiale și modul de rezolvare a acestora.

e) Ecuaţii cubice şi metode de rezolvare a acestora.

f) Ecuația biquadratică și metoda de rezolvare a acesteia.

g) Ecuații de gradul IV și metode de rezolvare a acestora.

g) Ecuaţii de grade înalte şi metode de rezolvare a acestora.

h) Ecuația algebrică rațională și metoda ei

i) Ecuaţii iraţionale şi metode de rezolvare a acestora.

j) Ecuații care conțin o necunoscută sub semn.

valoarea absolută și metoda de rezolvare a acesteia.

Ecuații transcendentale.

a) Ecuații exponențiale și modul de rezolvare a acestora.

b) Ecuaţii logaritmice şi metode de rezolvare a acestora.

Introducere

Educația matematică primită într-o școală cuprinzătoare este o componentă esențială a educației generale și a culturii generale a omului modern. Aproape tot ceea ce înconjoară omul modern este într-un fel legat de matematică. Iar progresele recente în fizică, inginerie și tehnologia informației nu lasă nicio îndoială că în viitor starea de lucruri va rămâne aceeași. Prin urmare, rezolvarea multor probleme practice se rezumă la rezolvarea diferitelor tipuri de ecuații pe care trebuie să înveți cum să le rezolvi.

Această lucrare este o încercare de a rezuma și sistematiza materialul studiat pe tema de mai sus. Am aranjat materialul în ordinea dificultății, începând cu cel mai simplu. Include atât tipurile de ecuații cunoscute nouă de la cursul școlar de algebră, cât și material suplimentar. În același timp, am încercat să arăt tipurile de ecuații care nu sunt studiate în cursul școlar, dar cunoașterea cărora poate fi necesară la intrarea într-o instituție de învățământ superior. În munca mea, la rezolvarea ecuațiilor, nu m-am limitat doar la soluția reală, ci am indicat și cea complexă, deoarece cred că altfel ecuația este pur și simplu nerezolvată. La urma urmei, dacă o ecuație nu are rădăcini reale, asta nu înseamnă că nu are soluții. Din păcate, din lipsă de timp, nu am putut să prezint tot materialul pe care îl am, dar chiar și cu materialul prezentat aici pot apărea multe întrebări. Sper că cunoștințele mele sunt suficiente pentru a răspunde la majoritatea întrebărilor. Așadar, încep să prezint materialul.

Matematica... dezvăluie ordinea,

simetrie și certitudine,

iar acestea sunt cele mai importante tipuri de frumusețe.

Aristotel.

Referință istorică

În acele vremuri îndepărtate, când înțelepții au început să se gândească la egalități care conțineau cantități necunoscute, probabil că nu existau monede sau portofele. Au existat însă grămezi, precum și oale și coșuri, care erau perfecte pentru rolul cache-urilor de depozitare care puteau ține un număr necunoscut de articole. „Căutăm o grămadă care, împreună cu două treimi, jumătate și o șapte, să facă 37...”, a învățat scribul egiptean Ahmes în mileniul II î.Hr. În vechile probleme de matematică din Mesopotamia, India, China, Grecia, cantitățile necunoscute exprimau numărul de păuni din grădină, numărul de tauri din turmă și totalitatea lucrurilor luate în considerare la împărțirea proprietății. Cărturarii, funcționarii și preoții inițiați în cunoștințele secrete, bine pregătiți în știința conturilor, au făcut față cu succes unor astfel de sarcini.

Surse care au ajuns la noi indică faptul că oamenii de știință antici aveau câteva tehnici generale pentru rezolvarea problemelor cu cantități necunoscute. Cu toate acestea, nici o tabletă de papirus sau lut nu conține o descriere a acestor tehnici. Autorii și-au furnizat doar ocazional calculele numerice cu comentarii sumbre, cum ar fi: „Uite!”, „Fă asta!”, „Ai găsit-o pe cea potrivită”. În acest sens, excepția este „Aritmetica” a matematicianului grec Diophantus din Alexandria (secolul al III-lea) - o colecție de probleme pentru alcătuirea ecuațiilor cu o prezentare sistematică a soluțiilor acestora.

Cu toate acestea, primul manual pentru rezolvarea problemelor care a devenit cunoscut pe scară largă a fost lucrarea savantului de la Bagdad din secolul al IX-lea. Muhammad bin Musa al-Khwarizmi. Cuvântul „al-jabr” din denumirea arabă a acestui tratat - „Kitab al-jaber wal-mukabala” („Cartea restaurării și a opoziției”) - s-a transformat de-a lungul timpului în binecunoscutul cuvânt „algebră”, iar al- Lucrarea lui Khwarizmi în sine a servit punctul de plecare în dezvoltarea științei rezolvării ecuațiilor.

ecuații Ecuații algebrice

Definiții de bază

În algebră, sunt luate în considerare două tipuri de egalități - identități și ecuații.

Identitate este o egalitate care este valabilă pentru toate valorile (admisibile) ale literelor incluse în ea). Pentru a înregistra identitatea, împreună cu semnul, se folosește și semnul.

Ecuația este o egalitate care este valabilă doar pentru anumite valori ale literelor incluse în ea. Literele incluse în ecuație, în funcție de condițiile problemei, pot fi inegale: unele își pot lua toate valorile permise (se numesc parametrii sau coeficienți ecuații și sunt de obicei notate cu primele litere ale alfabetului latin:, , ... - sau aceleași litere prevăzute cu indici: , , ... sau , , ...); se numesc altele ale căror valori trebuie găsite necunoscut(de obicei sunt desemnate prin ultimele litere ale alfabetului latin: , , , ... - sau aceleași litere prevăzute cu indici: , , ... sau , , ...).

În general, ecuația poate fi scrisă după cum urmează:

În funcție de numărul de necunoscute, ecuația se numește ecuație cu una, două necunoscute etc.

Valoarea necunoscutelor care transformă ecuația într-o identitate, numite soluții ecuații

Rezolvarea unei ecuații înseamnă a găsi multe dintre soluțiile acesteia sau a demonstra că nu există soluții. În funcție de tipul de ecuație, mulțimea de soluții ale ecuației poate fi infinită, finită sau goală.

Dacă toate soluțiile ecuației sunt soluții ale ecuației, atunci ei spun că ecuația este o consecință a ecuației și scrieți

Două ecuații

numit echivalent, dacă fiecare dintre ele este o consecință a celuilalt, și scrieți

Astfel, două ecuații sunt considerate echivalente dacă mulțimea soluțiilor acestor ecuații coincide.

O ecuație este considerată echivalentă cu două (sau mai multe) ecuații , dacă mulțimea soluțiilor ecuației coincide cu unirea mulțimilor de soluții a ecuațiilor , .

CATEVA ECUATII ECHIVALENTE:

Ecuația este echivalentă cu ecuația luată în considerare pe setul de valori admisibile ale ecuației inițiale.

Echivalent cu două ecuații și .

Ecuația este echivalentă cu ecuația.

Ecuația pentru n impar este echivalentă cu ecuația, iar pentru n par este echivalentă cu două ecuații și.

Ecuație algebrică numită ecuație a formei

unde este un polinom de grad al n-lea într-una sau mai multe variabile.

Ecuație algebrică cu o necunoscută se numeste ecuatie care se reduce la o ecuatie de forma

unde n este un număr întreg nenegativ; coeficienții polinomului , , , ..., , se numesc coeficienți(sau parametrii) ecuații și sunt considerate date; x este numit necunoscutși este ceea ce căutăm. Se numește numărul n grad ecuații

Se numesc valorile necunoscutului x care transformă ecuația algebrică într-o identitate rădăcini(mai rar decizii) ecuație algebrică.

Există mai multe tipuri de ecuații care pot fi rezolvate folosind formule gata făcute. Acestea sunt ecuații liniare și pătratice, precum și ecuații de forma F(x), unde F este una dintre funcțiile standard (funcție putere sau exponențială, logaritm, sinus, cosinus, tangentă sau cotangentă). Astfel de ecuații sunt considerate cele mai simple. Există și formule pentru ecuația cubică, dar nu este considerată cea mai simplă.

Deci, sarcina principală atunci când rezolvați orice ecuație este de a o reduce la cea mai simplă.

Toate ecuațiile enumerate mai jos au și propria lor soluție grafică, care constă în prezentarea părților stânga și dreaptă ale ecuației ca două funcții identice ale necunoscutului. Apoi se construiește un grafic, mai întâi al unei funcții, apoi al celeilalte, iar punctul (punctele) de intersecție a celor două grafice va da soluția (soluțiile) ecuației inițiale. În anexă sunt date exemple de soluții grafice ale tuturor ecuațiilor.

Ecuație liniară

Ecuație liniară se numește ecuație de gradul întâi.

unde a și b sunt numere reale.

O ecuație liniară are întotdeauna o singură rădăcină, care se găsește după cum urmează.

Adunând numărul la ambele părți ale ecuației (1), obținem ecuația

echivalent cu ecuația (1). Împărțind ambele părți ale ecuației (2) la valoarea , obținem rădăcina ecuației (1):

Ecuație cuadratică

Ecuația algebrică de gradul doi.

, (3)

unde , , sunt niște numere reale, numite ecuație pătratică. Dacă , atunci se numește ecuația pătratică (3). dat .

Rădăcinile unei ecuații pătratice sunt calculate folosind formula

Expresia se numește discriminant ecuație pătratică.

în care:

dacă , atunci ecuația are două rădăcini reale diferite;

dacă , atunci ecuația are o rădăcină reală a multiplicității 2;

dacă , atunci ecuația nu are rădăcini reale, dar are două rădăcini conjugate complexe:

, ,

Tipuri particulare de ecuație pătratică (3) sunt:

1) Ecuația pătratică redusă (dacă ), care se scrie de obicei sub forma

Rădăcinile ecuației pătratice date sunt calculate folosind formula

. (4)

Această formulă se numește formula lui Vieta, numită după matematicianul francez de la sfârșitul secolului al XVI-lea, care a adus o contribuție semnificativă la dezvoltarea simbolismului algebric.

2) O ecuație pătratică cu un al doilea coeficient par, care se scrie de obicei ca

(- întreg).

Este convenabil să calculați rădăcinile acestei ecuații pătratice folosind formula

. (5)

Formulele (4) și (5) sunt tipuri speciale de formule pentru calcularea rădăcinilor unei ecuații pătratice complete.

Rădăcinile ecuației pătratice reduse

sunt legate de coeficienții săi prin formulele Vieta

Dacă ecuația pătratică dată are rădăcini reale, formulele lui Vieta permit să se judece atât semnele, cât și mărimea relativă a rădăcinilor ecuației pătratice, și anume:

dacă , atunci ambele rădăcini sunt negative;

dacă , atunci ambele rădăcini sunt pozitive;

dacă , , atunci ecuația are rădăcini de semne diferite, iar rădăcina negativă este mai mare în valoare absolută decât cea pozitivă;

dacă , , ecuația are rădăcini de semne diferite, iar rădăcina negativă este mai mică decât rădăcina pozitivă în valoare absolută.

Să rescriem din nou ecuația pătratică

(6)

și vom arăta o altă modalitate de a deriva rădăcinile ecuației pătratice (6) prin coeficienții și termenul liber. Dacă

apoi rădăcinile ecuației pătratice se calculează folosind formula

, .

care poate fi obținută ca urmare a următoarelor transformări ale ecuației inițiale, precum și luând în considerare formula (7).

Rețineți că, prin urmare

dar, din formula (7) deci în final

Dacă punem acel +, atunci

Rețineți că, prin urmare

dar deci în cele din urmă

Ecuații binomiale

Ecuații de gradul al n-lea al formei

numit ecuație binomială. Cu și înlocuire)

unde este valoarea aritmetică a rădăcinii, ecuația (8) se reduce la ecuația

O ecuație binomială pentru n impar are o rădăcină reală. În mulțimea numerelor complexe, această ecuație are n rădăcini (dintre care una este reală și complexă):

( 0, 1, 2, ..., ). (9)

O ecuație binomială pentru n par din mulțimea numerelor reale are două rădăcini , iar în mulțimea numerelor complexe există n rădăcini, calculate prin formula (9).

O ecuație binomială pentru n par are o rădăcină reală, iar în mulțimea de numere complexe de rădăcini, calculată prin formula

( 0, 1, 2, ..., ). (10)

O ecuație binomială pentru n chiar nu are rădăcini reale. În setul de numere complexe, ecuația are rădăcini calculate folosind formula (10).

Să dăm un scurt rezumat al mulțimilor de rădăcini ale unei ecuații binomiale pentru unele valori specifice ale lui n.

Ecuația are două rădăcini reale.

Ecuația are două rădăcini reale și două rădăcini complexe.

Ecuația nu are rădăcini reale. Rădăcini complexe: .

Ecuația are o rădăcină reală și două rădăcini complexe

Ecuația nu are rădăcini reale. Rădăcini complexe:

, .

Ecuații cubice

Dacă matematicienii Babiloniei și Indiei antice au fost capabili să rezolve ecuații pătratice, atunci cele cubice, adică. ecuații ale formei

s-a dovedit a fi o nucă greu de spart. La sfârşitul secolului al XV-lea. Profesor de Matematică la Universitățile din Roma și Milano, Luca Pacioli, în celebrul său manual „Suma de cunoștințe despre aritmetică, geometrie, relații și proporționalitate” a pus problema găsirii unei metode generale de rezolvare a ecuațiilor cubice la egalitate cu problema pătratului. cercul. Și totuși, prin eforturile algebriștilor italieni, o astfel de metodă a fost găsită curând.

Să începem cu simplificarea

Dacă o ecuaţie cubică de formă generală

împărțit la , atunci coeficientul la devine egal cu 1. Prin urmare, în viitor vom merge din ecuație

La fel cum soluția unei ecuații pătratice se bazează pe formula pentru pătratul sumei, soluția unei ecuații cubice se bazează pe formula pentru cubul sumei:

Pentru a nu ne confunda în coeficienți, să înlocuim aici și să rearanjam termenii:

Vedem că alegând corect , și anume luând , ne putem asigura că partea dreaptă a acestei formule diferă de partea stângă a ecuației (11) doar în coeficientul at și termenul liber. Să adunăm ecuațiile (11) și (12) și să dăm unele similare:

Dacă facem o substituție aici, obținem o ecuație cubică față de fără termenul c:

Deci, am arătat că în ecuația cubică (11), folosind o substituție adecvată, putem scăpa de termenul care conține pătratul necunoscutului. Prin urmare, vom rezolva acum o ecuație de forma

. (13)

Formula Cardano

Să ne uităm din nou la formula cubului sumei, dar scrieți-o diferit:

Comparați această intrare cu ecuația (13) și încercați să stabiliți o legătură între ele. Chiar și cu un indiciu nu este ușor. Trebuie să aducem un omagiu matematicienilor Renașterii care au rezolvat ecuația cubică fără a cunoaște simbolismul alfabetic. Să înlocuim în formula noastră:

Acum este clar: pentru a găsi rădăcina ecuației (13), este suficient să rezolvi sistemul de ecuații

și luați ca sumă și . Prin înlocuirea , acest sistem se reduce la o formă foarte simplă:

Apoi puteți acționa în moduri diferite, dar toate „drumurile” vor duce la aceeași ecuație pătratică. De exemplu, conform teoremei lui Vieta, suma rădăcinilor ecuației pătratice reduse este egală cu coeficientul cu semnul minus, iar produsul este egal cu termenul liber. Rezultă că și sunt rădăcinile ecuației

Să scriem aceste rădăcini:

Variabilele și sunt egale cu rădăcinile cubice ale lui și , iar soluția dorită a ecuației cubice (13) este suma acestor rădăcini:

Această formulă este cunoscută ca Formula Cardano .

Soluție trigonometrică

, , . (14)

Rădăcinile , , ale ecuației cubice „incomplete” (14) sunt egale

, ,

Fie valabilă ecuația cubică „incompletă” (14).

a) Dacă (cazul „ireductibil”), atunci

(b) Dacă , , atunci

, ,

, .

, ,

, .

În toate cazurile, se ia valoarea reală a rădăcinii cubice.

Ecuație biquadratică

Ecuația algebrică de gradul al patrulea.

unde a, b, c sunt numere reale, numite ecuație biquadratică. Prin substituție, ecuația este redusă la o ecuație pătratică urmată de rezolvarea a două ecuații binomiale și ( și sunt rădăcinile ecuației patratice corespunzătoare).

Dacă și , atunci ecuația biquadratică are patru rădăcini reale:

, .

Dacă , ), atunci ecuația biquadratică are două rădăcini reale și rădăcini conjugate imaginare:

Dacă și , atunci ecuația biquadratică are patru rădăcini conjugate în perechi pur imaginare:

, .

Ecuații de gradul patru

O metodă de rezolvare a ecuațiilor de gradul al patrulea a fost găsită în secolul al XVI-lea. Ludovico Ferrari, elevul lui Gerolamo Cardano. Așa se numește - metoda. Ferrari .

Ca și în rezolvarea ecuațiilor cubice și pătratice, într-o ecuație de gradul al patrulea

poti scapa de termen prin substitutie. Prin urmare, vom presupune că coeficientul cubului necunoscutului este zero:

Ideea lui Ferrari a fost de a reprezenta ecuația sub forma , unde partea stângă este pătratul expresiei , iar partea dreaptă este pătratul unei ecuații liniare a , ai cărei coeficienți depind de . După aceasta, rămâne de rezolvat două ecuații pătratice: și . Desigur, o astfel de reprezentare este posibilă numai cu o alegere specială a parametrului. Este convenabil să o luați sub forma , apoi ecuația va fi rescrisă după cum urmează:

. (15)

Partea dreaptă a acestei ecuații este trinomul pătratic al lui . Va fi un pătrat complet atunci când discriminantul său este egal cu zero, adică.

, sau

Această ecuație se numește rezolutiv(adică „permisiv”). Este relativ cubic, iar formula lui Cardano ne permite să găsim unele dintre rădăcinile sale. Când partea dreaptă a ecuației (15) ia forma

iar ecuația în sine este redusă la două pătratice:

Rădăcinile lor dau toate soluțiile ecuației inițiale.

De exemplu, să rezolvăm ecuația

Aici va fi mai convenabil să folosiți nu formule gata făcute, ci însăși ideea soluției. Să rescriem ecuația sub forma

și adăugați expresia pe ambele părți, astfel încât să se formeze un pătrat complet pe partea stângă:

Acum să echivalăm discriminantul din partea dreaptă a ecuației cu zero:

sau, după simplificare,

Una dintre rădăcinile ecuației rezultate poate fi ghicită prin sortarea divizorilor termenului liber: . După înlocuirea acestei valori obținem ecuația

Unde . Rădăcinile ecuațiilor pătratice rezultate sunt Și . Desigur, în cazul general se pot obține și rădăcini complexe.

Soluția Descartes-Euler

prin substituire se reduce la o formă „incompletă”.

. (16)

Rădăcinile , , , ale ecuației de gradul al patrulea „incompletă” (16) sunt egale cu una dintre expresii

în care se aleg combinaţii de semne astfel încât condiţia să fie îndeplinită

unde , și sunt rădăcinile ecuației cubice

Ecuații de grad înalt

Solvabilitatea în radicali

Formula pentru rădăcinile unei ecuații pătratice este cunoscută din timpuri imemoriale și în secolul al XVI-lea. Algebriștii italieni au rezolvat ecuații de gradul al treilea și al patrulea în radicali. Astfel, s-a stabilit că rădăcinile oricărei ecuații care nu depășește gradul al patrulea sunt exprimate prin coeficienții ecuației printr-o formulă care utilizează doar patru operații aritmetice (adunare, scădere, înmulțire, împărțire) și extragerea rădăcinilor unui grad. nedepăşind gradul ecuaţiei. Mai mult, toate ecuațiile de un anumit grad () pot fi „servite” de o singură formulă generală. Prin înlocuirea coeficienților ecuației în ea, obținem toate rădăcinile - atât reale, cât și complexe.

După aceasta, a apărut firesc întrebarea: există formule generale similare pentru rezolvarea ecuațiilor de gradul al cincilea și mai sus? Răspunsul la aceasta a fost găsit de matematicianul norvegian Niels Henrik Abel la începutul secolului al XIX-lea. Puțin mai devreme, acest rezultat a fost indicat, dar nu suficient de fundamentat, de italianul Paolo Ruffini. Teorema Abel-Ruffini este astfel:

Ecuația generală a puterii la este de nerezolvat în radicali.

Astfel, nu există o formulă generală aplicabilă tuturor ecuațiilor de un anumit grad. Cu toate acestea, acest lucru nu înseamnă că este imposibil să se rezolve anumite tipuri particulare de ecuații de grade ridicate în radicali. Abel însuși a găsit o astfel de soluție pentru o clasă largă de ecuații de grad arbitrar ridicat - așa-numitele ecuații abeliene. Teorema Abel-Ruffini nici măcar nu exclude faptul că rădăcinile fiecărei ecuații algebrice specifice pot fi scrise prin coeficienții ei folosind semnele operațiilor aritmetice și radicalii, în special, că orice număr algebric, i.e. rădăcina unei ecuații de formă

cu coeficienți întregi, poate fi exprimat în radicali prin numere raționale. De fapt, o astfel de expresie nu există întotdeauna. Aceasta rezultă din teorema de solvabilitate pentru ecuațiile algebrice, construită de remarcabilul matematician francez Evariste Galois în „Memoria sa privind condițiile de solvabilitate a ecuațiilor în radicali” (1832; publicat în 1846).

Subliniem că în problemele aplicate ne interesează doar valorile aproximative ale rădăcinilor ecuației. Prin urmare, solvabilitatea sa în radicali nu joacă de obicei un rol aici. Există metode de calcul speciale care vă permit să găsiți rădăcinile oricărei ecuații cu orice precizie predeterminată, nu mai puțin decât cea oferită de calcule folosind formule gata făcute.

Ecuații care pot fi rezolvate

Deși ecuațiile de grade superioare sunt în general de nerezolvat în radicali, formulele lui Cardano și Ferrari pentru ecuațiile de gradul al treilea și al patrulea nu funcționează la școală în manualele de algebră și la examenele de admitere la facultate există uneori probleme în care trebuie să rezolvi ecuații mai mari decât cele; gradul doi. De obicei, acestea sunt special selectate, astfel încât rădăcinile ecuațiilor să poată fi găsite folosind unele tehnici elementare.

Una dintre aceste tehnici se bazează pe teorema despre rădăcinile raționale ale unui polinom:

Dacă o fracție ireductibilă este rădăcina unui polinom cu coeficienți întregi, atunci numărătorul ei este divizorul termenului liber, iar numitorul este divizorul coeficientului principal.

Pentru a dovedi, înlocuiți-o în ecuație și înmulțiți ecuația cu . Primim

Toți termenii din partea stângă, cu excepția ultimului, sunt divizibili cu , prin urmare este divizibil cu , și deoarece și sunt numere prime relativ, este un divizor al lui . Dovada pentru este similară.

Folosind această teoremă, puteți găsi toate rădăcinile raționale ale unei ecuații cu coeficienți întregi testând un număr finit de „candidați”. De exemplu, pentru ecuație

al cărui coeficient de conducere este 1, „candidații” vor fi divizori ai numărului –2. Sunt doar patru dintre ele: 1, -1, 2 și –2. Verificarea arată că doar unul dintre aceste numere este rădăcina: .

Dacă se găsește o rădăcină, puteți reduce gradul ecuației. Conform teoremei lui Bezout,

restul împărțirii unui polinom la un binom este egal cu , i.e.

Rezultă direct din teoremă că

Dacă este rădăcina unui polinom, atunci polinomul este împărțit la, adică unde este un polinom de gradul 1 mai mic decât.

Continuând exemplul nostru, să luăm din polinom

factor . Pentru a găsi coeficientul, puteți efectua împărțirea cu un colț:

Dar există o cale mai ușoară. Va deveni clar din exemplu:

Acum nu mai rămâne decât să rezolvăm ecuația pătratică . Rădăcinile sale:

Metoda coeficientului incert

Dacă un polinom cu coeficienți întregi nu are rădăcini raționale, puteți încerca să-l descompuneți în factori de grad inferior cu coeficienți întregi. Luați în considerare, de exemplu, ecuația

Să ne imaginăm partea stângă ca un produs a două trinoame pătrate cu coeficienți necunoscuți (nedefiniti):

Să deschidem parantezele din partea dreaptă și să dăm altele similare:

Acum, egalând coeficienții la aceleași puteri în ambele părți, obținem un sistem de ecuații

O încercare de a rezolva acest sistem într-o formă generală ne-ar duce înapoi la rezolvarea ecuației inițiale. Dar rădăcini întregi, dacă există, nu sunt greu de găsit prin selecție. Fără pierderea generalității, putem presupune că , atunci ultima ecuație arată că trebuie luate în considerare doar două opțiuni: , și . Înlocuind aceste perechi de valori în ecuațiile rămase, suntem convinși că prima dintre ele dă expansiunea dorită: . Această soluție se numește metoda coeficienților nedeterminați .

Dacă ecuația are forma , unde și sunt polinoame, atunci înlocuirea își reduce soluția la soluția a două ecuații de grade inferioare: și .

Ecuații reciproce

O ecuație algebrică reciprocă este o ecuație de grad par a formei

în care coeficienții, distanțați egal de capete, sunt egali cu: , etc. O astfel de ecuație se reduce la o ecuație de jumătate de grad prin împărțirea la și apoi înlocuirea .

Luați în considerare, de exemplu, ecuația

Împărțind-o la (ceea ce este legal, deoarece nu este o rădăcină), obținem

observa asta

Prin urmare, cantitatea satisface ecuația pătratică

rezolvare care poate fi găsită din ecuație .

Când rezolvă ecuații reciproce de grade superioare, de obicei folosesc faptul că expresia pentru oricare poate fi reprezentată ca un polinom de grad în .

Ecuații algebrice raționale

Raţional o ecuație algebrică este o ecuație de forma

Setul de valori admisibile ale ecuației algebrice raționale (17)

este dat de condiția, adică , , ..., unde , , ..., sunt rădăcinile polinomului.

Metoda de rezolvare a ecuației (17) este următoarea. Rezolvarea ecuației

ale căror rădăcini le notăm prin

Comparăm mulțimile de rădăcini ale polinoamelor și . Dacă nicio rădăcină a unui polinom nu este o rădăcină a unui polinom, atunci toate rădăcinile polinomului sunt rădăcini ale ecuației (17). Dacă orice rădăcină a unui polinom este rădăcina unui polinom, atunci este necesar să se compare din multiplicitate: dacă multiplicitatea rădăcinii polinomului este mai mare decât multiplicitatea rădăcinii polinomului, atunci această rădăcină este o rădăcină. (17) cu o multiplicitate egală cu diferența dintre multiplicitățile rădăcinilor dividendului și divizorului; în caz contrar, rădăcina polinomului nu este rădăcina ecuației raționale (17).

EXEMPLU Să găsim rădăcinile reale ale ecuației

Unde , .

Polinomul are două rădăcini reale (ambele simple):

Un polinom are o rădăcină simplă. Prin urmare, ecuația are o rădăcină reală.

Rezolvând aceeași ecuație în mulțimea numerelor complexe, constatăm că ecuația are, pe lângă rădăcina reală indicată, două rădăcini conjugate complexe:

Ecuații iraționale

O ecuație care conține o necunoscută (sau o expresie algebrică rațională pentru o necunoscută) sub semnul radical se numește ecuație irațională. În matematica elementară, soluțiile ecuațiilor iraționale se găsesc în mulțimea numerelor reale.

Orice ecuație irațională poate fi redusă la o ecuație algebrică rațională folosind operații algebrice elementare (înmulțire, împărțire, ridicarea ambelor părți ale ecuației la o putere întreagă). Trebuie avut în vedere faptul că ecuația algebrică rațională rezultată se poate dovedi a fi neechivalentă cu ecuația irațională originală, și anume, poate conține rădăcini „extra” care nu vor fi rădăcini ale ecuației iraționale originale. Prin urmare, după ce s-au găsit rădăcinile ecuației algebrice raționale rezultate, este necesar să se verifice dacă toate rădăcinile ecuației raționale vor fi rădăcinile ecuației iraționale.

În cazul general, este dificil de indicat vreo metodă universală de rezolvare a oricărei ecuații iraționale, deoarece este de dorit ca, ca urmare a transformărilor ecuației iraționale originale, rezultatul să nu fie doar o ecuație algebrică rațională, printre rădăcinile lui care vor fi rădăcinile ecuației iraționale date, ci o ecuație algebrică rațională formată din polinoame de cel mai mic grad posibil. Dorința de a obține acea ecuație algebrică rațională formată din polinoame de un grad cât mai mic este destul de firească, deoarece găsirea tuturor rădăcinilor unei ecuații algebrice raționale în sine se poate dovedi a fi o sarcină destul de dificilă, pe care o putem rezolva complet doar într-un număr foarte limitat de cazuri.

Să prezentăm câteva metode standard, cele mai frecvent utilizate pentru rezolvarea ecuațiilor algebrice iraționale.

1) Una dintre cele mai simple metode de rezolvare a ecuațiilor iraționale este metoda eliminării radicalilor prin ridicarea succesivă a ambelor părți ale ecuației la puterea naturală corespunzătoare. Trebuie avut în vedere că atunci când ambele părți ale ecuației sunt ridicate la o putere impară, ecuația rezultată este echivalentă cu cea inițială, iar când ambele părți ale ecuației sunt ridicate la o putere pară, ecuația rezultată va, în general vorbind, să nu fie echivalent cu ecuația originală. Acest lucru poate fi ușor verificat prin ridicarea ambelor părți ale ecuației

în orice grad. Rezultatul acestei operații este ecuația

a cărui mulțime de soluții este o uniune de mulțimi de soluții:

ȘI .

Cu toate acestea, în ciuda acestui dezavantaj, procedura de ridicare a ambelor părți ale ecuației la o putere (deseori chiar) este cea mai comună procedură pentru reducerea unei ecuații iraționale la o ecuație rațională.

unde , , sunt unele polinoame.

Datorită definiției operației de extragere a unei rădăcini în mulțimea numerelor reale, valorile admisibile ale necunoscutului sunt determinate de condițiile

Punând la pătrat ambele părți ale ecuației (18), obținem ecuația

După pătrat din nou, ecuația devine o ecuație algebrică

Deoarece ambele părți ale ecuației (18) au fost pătrate, se poate dovedi că nu toate rădăcinile ecuației (19) vor fi soluții ale ecuației inițiale este necesară verificarea rădăcinilor.

2) Un alt exemplu de rezolvare a ecuațiilor iraționale este metoda introducerii de noi necunoscute, în raport cu care se obține fie o ecuație irațională mai simplă, fie o ecuație rațională.

Exemplul 2. Rezolvați o ecuație irațională

Setul de valori valide pentru această ecuație este:

Punând , după înlocuire obținem ecuația

sau o ecuație echivalentă

care poate fi considerată ca o ecuaţie pătratică în raport cu . Rezolvând această ecuație, obținem

Prin urmare, setul de soluții al ecuației iraționale inițiale este uniunea mulțimilor de soluții ale următoarelor două ecuații:

, .

Ridicând ambele părți ale fiecăreia dintre aceste ecuații la un cub, obținem două ecuații algebrice raționale:

, .

Rezolvând aceste ecuații, aflăm că această ecuație irațională are o singură rădăcină.

În concluzie, observăm că atunci când rezolvăm ecuații iraționale, nu ar trebui să începem rezolvarea ecuației prin ridicarea ambelor părți ale ecuației la o putere naturală, încercând să reducem soluția ecuației iraționale la soluția unei ecuații algebrice raționale. Mai întâi trebuie să vedem dacă este posibil să facem o transformare identică a ecuației care poate simplifica semnificativ soluția acesteia.

. (20)

Setul de valori acceptabile pentru această ecuație este: . Să facem următoarele transformări ale acestei ecuații:

ecuația nu va avea soluții;

când ecuația poate fi scrisă ca

Când această ecuație nu are soluții, deoarece pentru orice , aparținând mulțimii de valori admisibile ale ecuației, expresia din partea stângă a ecuației este pozitivă.

Când ecuația are o soluție

Tinand cont ca multimea solutiilor admisibile ale ecuatiei este determinata de conditia , obtinem in final:

La rezolvarea ecuației iraționale (20) va exista

Pentru toate celelalte valori, ecuația nu are soluții, adică mulțimea soluțiilor sale este o mulțime goală.

Ecuații care conțin o necunoscută sub semnul valorii absolute

Ecuațiile care conțin o necunoscută cu semn de valoare absolută pot fi reduse la ecuații fără semn de valoare absolută folosind definiția modulului. Deci, de exemplu, rezolvarea ecuației

(21)

reduce la rezolvarea a două ecuații cu condiții suplimentare.

1) Dacă , atunci ecuația (21) se reduce la forma

. (22)

Soluții la această ecuație: , . Condiția este îndeplinită de a doua rădăcină a ecuației pătratice (22), iar numărul 3 este rădăcina ecuației (21).

2) Dacă , ecuația (21) se reduce la forma

Rădăcinile acestei ecuații sunt numerele Și . Prima rădăcină nu îndeplinește condiția și, prin urmare, nu este o soluție a acestei ecuații (21).

Astfel, soluțiile ecuației (21) vor fi numerele 3 și .

Rețineți că coeficienții unei ecuații care conține o necunoscută sub semnul valorii absolute pot fi selectați în așa fel încât soluțiile ecuației să fie toate valorile necunoscutului aparținând unui anumit interval al axei numerice. De exemplu, să rezolvăm ecuația

. (23)

Să ne uităm la axa numerică Ox și să marchem punctele 0 și 3 pe ea (zerouri de funcții sub semnul valorii absolute). Aceste puncte vor împărți linia numerică în trei intervale (Fig. 1):

1) Când ecuația (23) se reduce la forma

În interval, ultima ecuație nu are soluții.

În mod similar, atunci când ecuația (23) este redusă la forma

iar in interval nu are solutii.

2) Când ecuația (23) se reduce la forma

adică se transformă în identitate. Prin urmare, orice valoare este o soluție a ecuației (23).

Ecuații transcendentale

Se numește o ecuație care nu poate fi redusă la o ecuație algebrică folosind transformări algebrice ecuație transcendentală ).

Cele mai simple ecuații transcendentale sunt ecuațiile exponențiale, logaritmice și trigonometrice.

Ecuații exponențiale

Ecuație exponențială este o ecuație în care necunoscuta este inclusă numai în exponenții unor baze constante.

Cea mai simplă ecuație exponențială, a cărei soluție se reduce la soluția unei ecuații algebrice, este o ecuație de forma

unde și sunt câteva numere pozitive. Ecuația exponențială (24) este echivalentă cu ecuația algebrică

În cel mai simplu caz, când , ecuația exponențială (24) are soluție

Mulțimea soluțiilor unei ecuații exponențiale de forma

unde este un polinom, găsit după cum urmează.

Se introduce o nouă variabilă, iar ecuația (25) este rezolvată ca algebrică în raport cu necunoscutul. După aceasta, rezolvarea ecuației inițiale (25) se reduce la rezolvarea celor mai simple ecuații exponențiale de forma (24).

Exemplul 1. Rezolvați ecuația

Scrierea ecuației sub formă

și introducând o nouă variabilă, obținem o ecuație cubică în raport cu variabila:

Este ușor de verificat că această ecuație cubică are o singură rădăcină rațională și două rădăcini iraționale: și .

Astfel, rezolvarea ecuației inițiale se reduce la rezolvarea celor mai simple ecuații exponențiale:

Ultimul listat nu are ecuații de soluție. Setul de soluții la prima și a doua ecuație:

Unele dintre cele mai simple ecuații ale indicatorului:

1) Ecuația formei

2) Ecuația formei

înlocuirea se reduce la o ecuație pătratică

3) Ecuația formei

înlocuirea se reduce la o ecuație pătratică

Ecuații logaritmice

Logaritmic O ecuație este o ecuație în care necunoscutul apare ca argument pentru o funcție logaritmică.

Cea mai simplă ecuație logaritmică este o ecuație de formă

, (26)

unde este un număr pozitiv diferit de unul, este orice număr real. Ecuația logaritmică (26) este echivalentă cu ecuația algebrică

În cel mai simplu caz, când , ecuația logaritmică (26) are o soluție

Mulțimea soluțiilor unei ecuații logaritmice de forma , unde este un polinom al necunoscutului specificat, se găsește după cum urmează.

Se introduce o nouă variabilă, iar ecuația (25) este rezolvată ca o ecuație algebrică pentru . După aceasta se rezolvă cele mai simple ecuații logaritmice de forma (25).

Exemplul 1. Rezolvați ecuația

Raportat la necunoscut, această ecuație este pătratică:

Rădăcinile acestei ecuații sunt: , .

Rezolvarea ecuațiilor logaritmice

obţinem soluţii la ecuaţia logaritmică (27): , .

În unele cazuri, pentru a reduce soluția unei ecuații logaritmice la soluția secvențială a ecuațiilor algebrice și logaritmice simple, este necesar să se facă mai întâi transformări adecvate ale logaritmilor incluși în ecuație. Astfel de transformări pot fi transformarea sumei logaritmilor a două mărimi în logaritmul produsului acestor mărimi, trecerea de la un logaritm cu o bază la un logaritm cu altă bază etc.

Exemplul 2. Rezolvați ecuația

Pentru a reduce soluția acestei ecuații la o soluție secvențială de ecuații algebrice și logaritmice simple, este necesar în primul rând reducerea tuturor logaritmilor la o singură bază (aici, de exemplu, la baza 2). Pentru a face acest lucru, folosim formula

în virtutea căreia . Înlocuind o valoare egală în ecuația (28), obținem ecuația

Înlocuire această ecuație se reduce la o ecuație pătratică pentru necunoscutul:

Rădăcinile acestei ecuații pătratice sunt: , . Rezolvăm ecuații și :

Exemplul 3. Rezolvați ecuația

Conversia diferenței dintre logaritmii a două mărimi în logaritmul coeficientului acestor mărimi:

reducem această ecuație la cea mai simplă ecuație logaritmică

Concluzie

Matematica, ca orice altă știință, nu stă pe loc odată cu dezvoltarea societății, opiniile oamenilor se schimbă, apar noi gânduri și idei. Iar secolul XX nu a făcut excepție în acest sens. Apariția computerelor a făcut ajustări la metodele de rezolvare a ecuațiilor și le-a făcut mult mai ușoare. Dar un computer poate să nu fie întotdeauna la îndemână (examen, test), așa că este necesară cunoașterea cel puțin a celor mai importante modalități de rezolvare a ecuațiilor. Utilizarea ecuațiilor în viața de zi cu zi este rară. Și-au găsit aplicația în multe sectoare ale economiei și în aproape toate cele mai noi tehnologii.

În această lucrare nu au fost prezentate toate metodele de rezolvare a ecuațiilor și nici măcar toate tipurile acestora, ci doar cele mai elementare. Sper că eseul meu poate servi ca un bun material de referință atunci când rezolv anumite ecuații. În concluzie, aș dori să remarc că atunci când am scris acest eseu, nu mi-am propus scopul de a arăta toate tipurile de ecuații, ci am prezentat doar materialul pe care îl aveam.

Lista literaturii folosite

Cap. ed. M. D. Aksenova. Enciclopedie pentru copii. Volumul 11. Matematică. – M.: Avanta+, 1998. – 688 p.

Tsypkin A.G. Ed. S. A. Stepanova. Manual de matematică pentru liceu. – M.: Nauka, 1980.- 400 p.

G. Korn şi T. Korn. Manual de matematică pentru oameni de știință și ingineri. – M.: Nauka, 1970.- 720 p.

) Sub acceptabil Se înțeleg acele valori numerice ale literelor pentru care toate operațiunile efectuate asupra literelor incluse în egalitate sunt fezabile. De exemplu, valorile valide ale literelor incluse în egalitate

vor fi următoarele; Pentru ; pentru, pentru

) Dacă a și b au semne diferite, atunci .

) Cazul este similar cu cel discutat.

) Sub transformări algebrice ecuații

Înțelegeți următoarele transformări:

1) adăugarea aceleiași expresii algebrice la ambele părți ale ecuației;

2) înmulțirea ambelor părți ale ecuației cu aceeași expresie algebrică;

3) ridicarea ambelor părți ale ecuației la o putere rațională.

Ministerul Educației Generale și Profesionale al Federației Ruse

Instituție de învățământ municipală

Gimnaziul nr 12

compoziţie

pe tema: Ecuaţii şi metode de rezolvare a acestora

Completat de: elev clasa a 10-a „A”

Krutko Evgheni

Verificat de: profesor de matematică Iskhakova Gulsum Akramovna

Tyumen 2001

Plan................................................. .................................................. ...... ................................ 1

Introducere................................................. ....... ................................................. ............. ................................ 2

Parte principală................................................ .................................................. ...... ............... 3

Concluzie................................................. .................................................. ...... ............... 25

Aplicație............................................................. .................................................. ...... ................ 26

Lista literaturii utilizate.................................................. ........... ................................. 29

Plan.

Introducere.

Referință istorică.

Ecuații. Ecuații algebrice.

a) Definiții de bază.

b) Ecuația liniară și metoda de rezolvare a acesteia.

c) Ecuaţii pătratice şi metode de rezolvare a acestora.

d) Ecuații binomiale și modul de rezolvare a acestora.

e) Ecuaţii cubice şi metode de rezolvare a acestora.

f) Ecuația biquadratică și metoda de rezolvare a acesteia.

g) Ecuații de gradul IV și metode de rezolvare a acestora.

g) Ecuaţii de grade înalte şi metode de rezolvare a acestora.

h) Ecuația algebrică rațională și metoda ei

i) Ecuaţii iraţionale şi metode de rezolvare a acestora.

j) Ecuații care conțin o necunoscută sub semn.

valoarea absolută și metoda de rezolvare a acesteia.

Ecuații transcendentale.

a) Ecuații exponențiale și modul de rezolvare a acestora.

b) Ecuaţii logaritmice şi metode de rezolvare a acestora.

Introducere

Matematica... dezvăluie ordinea,

simetrie și certitudine,

iar acestea sunt cele mai importante tipuri de frumusețe.

Aristotel.

Referință istorică

ecuații Ecuații algebrice

Definiții de bază

În algebră, sunt luate în considerare două tipuri de egalități - identități și ecuații.

Identitate este o egalitate care este valabilă pentru toate valorile (admisibile) ale literelor incluse în ea). Pentru a înregistra o identitate împreună cu un semn

se foloseste si semnul.

, , ... - sau aceleași litere prevăzute cu indici: , , ... sau , , ...); se numesc altele ale căror valori trebuie găsite necunoscut(de obicei sunt desemnate prin ultimele litere ale alfabetului latin: , , , ... - sau aceleași litere prevăzute cu indici: , , ... sau , , ...).

În general, ecuația poate fi scrisă după cum urmează:

( , , ..., ) .

În funcție de numărul de necunoscute, ecuația se numește ecuație cu una, două necunoscute etc.

Valoarea necunoscutelor care transformă ecuația într-o identitate, numite soluții ecuații

Dacă toate soluțiile ecuației

sunt soluții ale ecuației

Tipuri de ecuații algebrice și metode de rezolvare a acestora

Pentru studenții interesați de matematică, la rezolvarea ecuațiilor algebrice de grade superioare, o metodă eficientă de găsire rapidă a rădăcinilor, împărțind cu rest la binomul x -  sau la ax + b, este schema Horner.

Luați în considerare schema lui Horner.

Să notăm câtul incomplet la împărțirea P(x) la x –  prin

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, iar restul este b n.

Deoarece P(x) = Q (x)(x–) + b n, atunci egalitatea este valabilă

un 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х– ) + b n

Să deschidem parantezele din partea dreaptă și să comparăm coeficienții pentru aceleași puteri ale lui x din stânga și din dreapta. Obţinem că a 0 = b 0 şi pentru 1  k  n sunt valabile relaţiile a k = b k -  b k -1. Rezultă că b 0 = a 0 și b k = a k +  b k -1, 1  k  n.

Scriem calculul coeficienților polinomului Q (x) și restul b n sub forma unui tabel:

un 0

a 1

a 2

A n-1

A n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Exemplul 1. Împărțiți polinomul 2x 4 – 7x 3 – 3x 2 + 5x – 1 la x + 1.

Soluţie. Folosim schema lui Horner.

Când împărțim 2x 4 – 7x 3 – 3x 2 + 5x – 1 la x + 1 obținem 2x 3 – 9x 2 + 6x – 1

Raspuns: 2 x 3 – 9x 2 + 6x – 1

Exemplul 2. Calculați P(3), unde P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Soluţie. Folosind teorema lui Bezout și schema lui Horner, obținem:

Răspuns: P(3) = 535

Exercițiu

Folosind diagrama lui Horner, împărțiți polinomul

4x 3 – x 5 + 132 – 8x 2 pe x + 2;

2) Împărțiți polinomul

2x 2 – 3x 3 – x + x 5 + 1 pe x + 1;

3) Aflați valoarea polinomului P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 pentru x = 7.

1.1. Găsirea rădăcinilor raționale ale ecuațiilor cu coeficienți întregi

Metoda de găsire a rădăcinilor raționale ale unei ecuații algebrice cu coeficienți întregi este dată de următoarea teoremă.

Teorema: Dacă o ecuație cu coeficienți întregi are rădăcini raționale, atunci ele sunt câtul împărțirii divizorului termenului liber la divizorul coeficientului principal.

Dovada: a 0 x n + a 1 x n -1 + … + a n = 0

Fie x = p/ q este o rădăcină rațională, q, p sunt coprime.

Înlocuind fracția p/q în ecuație și eliberându-ne de numitor, obținem

a 0 r n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

Să rescriem (1) în două moduri:

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

a 0 r n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

Din egalitatea (2) rezultă că a n q n este divizibil cu p, iar din moment ce q n și p sunt între prime, atunci a n este divizibil cu p. În mod similar, din egalitatea (3) rezultă că a 0 este divizibil cu q. Teorema a fost demonstrată.

Exemplul 1. Rezolvați ecuația 2x 3 – 7x 2 + 5x – 1 = 0.

Soluţie. Ecuația nu are rădăcini întregi găsim rădăcinile raționale ale ecuației. Fie fracția ireductibilă p /q rădăcina ecuației, atunci p se găsește printre divizorii termenului liber, adică. dintre numerele  1, și q dintre divizorii pozitivi ai coeficientului principal: 1; 2.

Acestea. rădăcinile raționale ale ecuației trebuie căutate printre numerele  1,  1/2, notează P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1)  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 este rădăcina ecuației.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

Primim: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1)(x 2 – 3x + 1) = 0.

Echivalând al doilea factor cu zero și rezolvând ecuația, obținem

Răspuns:
,

Exerciții

Rezolvarea ecuațiilor:

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Ecuații reciproce și metode de rezolvare

Definiție. O ecuație cu puteri întregi în raport cu o necunoscută se numește recurentă dacă coeficienții ei, echidistanți de capetele părții stângi, sunt egali între ei, adică. ecuația formei

A x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Ecuație reciprocă de grad impar

A x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

are întotdeauna o rădăcină x = – 1. Prin urmare, este echivalent cu combinarea ecuației x + 1 = 0 și  x 2 n +  x 2 n -1 + … +  x +  = 0. Ultima ecuație este a ecuație reciprocă de grad par. Astfel, rezolvarea ecuațiilor reciproce de orice grad se reduce la rezolvarea unei ecuații reciproce de grad par.

Cum să o rezolv? Să fie dată o ecuație reciprocă de grad par

A x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

Rețineți că x = 0 nu este o rădăcină a ecuației. Apoi împărțim ecuația la x n, obținem

A x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + ax -n = 0

Grupăm termenii din partea stângă în perechi

A( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1 ) + e = 0

Facem înlocuirea x + x -1 = y. După înlocuirea expresiilor x 2 + x -2 = y 2 – 2;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 în ecuație obținem ecuația pentru laАу n + Prin n -1 +Cy n -2 + … + Ey + D = 0.

Pentru a rezolva această ecuație, trebuie să rezolvați mai multe ecuații pătratice de forma x + x -1 = y k, unde k = 1, 2, ... n. Astfel, obținem rădăcinile ecuației inițiale.

Exemplul 1. Rezolvați ecuația x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0.

Soluţie. x = – 1 este rădăcina ecuației. Să aplicăm schema lui Horner.

Ecuația noastră va lua forma:

(x + 1)(x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Grupând, obținem: .

Să introducem un înlocuitor:
;
;
.

Primim relativ la ecuația: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) – 9 (y + 1) = 0; (y + 1)(y 2 – 9); y 1 = -1, y 2,3 =  3.

Rezolvarea ecuațiilor
,
,
,

obținem rădăcinile:
,
,
,

Raspuns: x 1 = -1,
,

Exerciții

Rezolvați ecuații.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Metoda de înlocuire a variabilelor pentru rezolvarea ecuațiilor

Metoda înlocuirii variabilelor este cea mai comună metodă. Arta de a face o schimbare variabilă este de a vedea care schimbare are cel mai mult sens și va duce la succes mai repede.

Dacă se dă ecuația

F(f(x)) = 0, (1)

apoi prin înlocuirea necunoscutei y = f (x) se reduce mai întâi la ecuație

F(y) = 0, (2)

și apoi după găsirea tuturor soluțiilor ecuației (2) y 1, y 2, ..., y n, ... se reduce la rezolvarea mulțimii de ecuații f (x) = y 1, f (x) = y 2 ,..., f (x) = y 2,...

Principalele moduri de implementare a metodei de înlocuire a variabilelor sunt:

folosind proprietatea de bază a unei fracții;

evidentierea patratului binomului;

trecerea la un sistem de ecuații;

paranteze de deschidere în perechi;

deschiderea parantezelor în perechi și împărțirea ambelor părți ale ecuației;

scăderea gradului ecuației;

înlocuire dublă.

1.3.1. Reducerea puterii unei ecuații

Rezolvați ecuația (x 2 + x + 2)(x 2 + x + 3) = 6 (3)

Soluţie. Să notăm x 2 + x + 2 = y, apoi să luăm y (y + 1) = 6, rezolvând pe acesta din urmă, obținem y 1 = 2, y 2 = -3. Această ecuație (3) este echivalentă cu setul de ecuații x 2 + x + 2 = 2

x 2 + x + 2 = -3

Rezolvând primul, obținem x 1 = 0, x 2 = -1. Rezolvând a doua, obținem
,

Răspuns: x 1 = 0, x 2 = -1,

1.3.2. Ecuația de gradul al patrulea de forma (x + a)(x +b )(X + c )(X + d ) = m , unde a + b = c + d sau a + c = b + d sau a + d = b + c.

Exemplu. Rezolvați ecuația (x - 1)(x - 7)(x -4)(x + 2) = 40

Soluţie. – 1- 4 = - 7 + 2, - 5 = - 5, înmulțind aceste perechi de paranteze, obținem ecuația (x 2 - 5x - 14)(x 2 - 5x + 4) = 40

Să introducem înlocuirea: x 2 - 5x – 14 = y, obținem ecuația y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0. y 1 = -20, y 2 = 2. Revenind la variabila inițială, rezolvăm un set de ecuații:

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3,4 =

Răspuns: x 1 = 2; x 2 = 3 x 3,4 =

1.3.3. O ecuație de forma (x + a)(x + b)(x + c)(x + d) = Ex 2,

Unde ab = cd, sau ac =bd, sau ad = bc. Deschideți parantezele în perechi și împărțiți ambele părți la x 2  0.

Exemplu. (x - 1)(x - 2)(x - 8)(x - 4) = 4x 2

Soluţie. Produsul numerelor din primul și al treilea și din al doilea și al patrulea parantez este egal, adică. – 8 (- 1) = (- 2)(- 4). Să înmulțim perechile indicate de paranteze și să scriem ecuația (x 2 - 9x + 8)(x 2 - 6x + 8) = 4x 2.

Deoarece x = 0 nu este o rădăcină a ecuației, împărțim ambele părți ale ecuației la x 2  0, obținem:
, înlocuire:
, ecuația inițială va lua forma:t(t+3) =4, t 2 + 3 t=4, t 2 + 3 t – 4=0, t 1 =1, t 2 = - 4.

Să revenim la variabila inițială:

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

Rezolvăm prima ecuație, obținem x 1,2 = 5 

A doua ecuație nu are rădăcini.

Răspuns: x 1,2 = 5 

1.3.4. Ecuația celui de-al patrulea tip (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Ecuația (ax 2 + b 1 x+ c)(A x 2 + b 2 X + c) = A x 2, unde c  0, A  2
, care după înlocuirea necunoscutului
poate fi rescris ca un pătrat și poate fi rezolvat cu ușurință.

Exemplu. (x 2 + x+ 2)(x 2 + 2x + 2) = 2x 2

Soluţie. Este ușor de observat că x = 0 nu este o rădăcină a acestei ecuații împărțind această ecuație la x 2 , obținem ecuația

înlocuire
, obținem ecuația (y+1)(y+2) = 2, rezolvând-o, avem rădăcini y 1 = 0; la 2 = - 3, prin urmare ecuația originală este echivalentă cu setul de ecuații

rezolvând, obținem x 1 = -1; x 2 = -2.

Răspuns: x 1 = -1; x 2 = -2

1.3.5. Ecuația de forma: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

Ecuația A(cx 2 + p 1 X + q) 2 + b(cx 2 + p 2 X + q) 2 = Topor 2 unde A, b, c, q, A sunt astfel încât q 0, A 0, c 0, A 0, b 0 nu are rădăcină x = 0, deci împărțind ecuația la x 2 , obținem o ecuație echivalentă
, care după înlocuire
poate fi rescrisă ca o ecuație pătratică care poate fi rezolvată cu ușurință. + 1)( x 2 – 14x + 15 = 0

X 2 – 7 X + 15 = 0

Răspuns:

Ecuație liniară este o ecuație algebrică. În această ecuație, gradul total al polinoamelor sale constitutive este egal cu unu.

Ecuațiile liniare sunt prezentate după cum urmează:

În formă generală: A 1 X 1 + A 2 X 2 + … + un n x n + b = 0

În formă canonică: a 1 x 1 + a 2 x 2 + … + a n x n = b.

Ecuație liniară cu o variabilă.

O ecuație liniară cu 1 variabilă se reduce la forma:

topor+ b=0.

De exemplu:

2x + 7 = 0. Unde a=2, b=7;

0,1x - 2,3 = 0. Unde a=0,1, b=-2,3;

12x + 1/2 = 0. Unde a=12, b=1/2.

Numărul de rădăcini depinde de AȘi b:

Când A= b=0 , ceea ce înseamnă că ecuația are un număr nelimitat de soluții, deoarece .

Când A=0 , b≠ 0 , ceea ce înseamnă că ecuația nu are rădăcini, deoarece .

Când A ≠ 0 , ceea ce înseamnă că ecuația are o singură rădăcină.

Ecuație liniară cu două variabile.

Ecuația cu variabila X este o egalitate de tip A(x)=B(x), Unde Topor)Și B(x)- expresii din X. La înlocuirea setului T valorile Xîn ecuație obținem o egalitate numerică adevărată, care se numește set de adevăr această ecuaţie sau rezolvarea unei ecuații date, și toate aceste valori ale variabilei sunt rădăcinile ecuației.

Ecuațiile liniare a 2 variabile sunt prezentate în următoarea formă:

În formă generală: ax + by + c = 0,

În formă canonică: ax + by = -c,

În formă de funcție liniară: y = kx + m, Unde .

Soluția sau rădăcinile acestei ecuații sunt următoarea pereche de valori variabile (X y), care o transformă într-o identitate. O ecuație liniară cu 2 variabile are un număr nelimitat de aceste soluții (rădăcini). Modelul geometric (graficul) al acestei ecuații este o linie dreaptă y=kx+m.

Dacă o ecuație conține x pătrat, atunci ecuația se numește

Matematică. Algebră. Geometrie. Trigonometrie

ALGEBRA: Ecuații și sisteme de ecuații

4.2. Tipuri de ecuații și metode de rezolvare a acestora

În cazul în care este necesar să găsim valorile unei variabile care satisfac ambele ecuații date, spunem că este dată, sistem de ecuații. O acoladă este folosită pentru a indica un sistem:

Mai multe ecuații cu o formă variabilă set de ecuații, dacă sarcina este de a găsi toate aceste valori ale unei variabile, fiecare dintre acestea fiind rădăcina a cel puțin uneia dintre aceste ecuații. O paranteză pătrată este folosită pentru a indica o populație:

Ecuații care conțin o variabilă sub semnul modulului.

Valoarea absolută a unui număr A este definită după cum urmează:

Exemplu: Rezolvați ecuația

Soluție: Dacă

, Acea

. O poti scrie asa:

Din Eq.

găsim X= -9. Cu toate acestea, cu această valoare a variabilei, inegalitatea nu este valabilă, ceea ce înseamnă că valoarea găsită nu este rădăcina acestei ecuații., Acea

iar această ecuație va lua forma. O poti scrie asa:

Din Eq.

găsim . Inegalitatea este adevărată, ceea ce înseamnă - rădăcina acestei ecuații.. Ecuații cu o variabilă la numitor.

Luați în considerare ecuații de formă

. (1)

Rezolvarea unei ecuații de tip (1) se bazează pe următoarea afirmație: o fracție este egală cu 0 dacă și numai dacă numărătorul ei este egal cu 0 și numitorul ei este diferit de zero.

În conformitate cu cele de mai sus, soluția ecuației

se desfășoară în două etape: mai întâi trebuie să rezolvați ecuațiași apoi aflați dacă, cu valorile găsite ale variabilei, X numitor la 0. Dacă q(x) ¹ 0 , apoi rădăcina găsită a ecuațieieste, de asemenea, rădăcina ecuației (1); Dacăq(x) = 0, apoi rădăcina rezultată a ecuațieieste, de asemenea, rădăcina ecuației (1). Sistemul rezultat este: Domeniul ecuației
f(x) = g(x) numiți mulțimea tuturor acelor valori ale unei variabile X, pentru care expresiaf(x), și expresia g(x)are sens.

Dacă în procesul de transformare a unei ecuații domeniul său de definiție s-a extins, atunci pot apărea rădăcini străine. Prin urmare, toate valorile găsite ale variabilei trebuie verificate prin înlocuire în ecuația originală sau folosind domeniul de definire al ecuației originale.

Ecuații raționale.

Ecuația

f(x) = g(x) numit raţional, Dacă f(x) și g(x)-expresii raţionale. Mai mult, dacă f(x) și g(x)- expresii întregi, atunci se numește ecuația întreg ;dacă măcar una dintre expresiif(x), g(x)este fracționară, apoi ecuația raționalăf(x) = g(x) numit fracționat .

Pentru a rezolva o ecuație rațională, aveți nevoie de:

găsiți numitorul comun al tuturor fracțiilor disponibile;
înlocuiți această ecuație cu una întreagă, înmulțind ambele părți cu un numitor comun;
Rezolvați întreaga ecuație rezultată;
Eliminați din rădăcini pe cele care fac să dispară numitorul comun.

Rezolvarea ecuației
p(x) = 0 metoda factorizării. p(x) poate fi factorizat: , apoi ecuația ia forma

. Dacă A- rădăcina ecuației, Acea

, deci cel puțin unul dintre numere

este egal cu 0.

Este adevărat și contrariul: dacă X

= A- rădăcina a cel puțin uneia dintre ecuații , , , Acea A- rădăcina ecuației. Acesta este Rezolvarea ecuațiilor
prin introducerea unei noi variabile.

Să explicăm esența metodei cu un exemplu.

Exemplu: Rezolvați ecuația

Soluție

, obținem ecuația

, unde găsim

. Problema se rezumă la rezolvarea unui set de ecuații

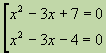
Prima ecuație pătratică nu are rădăcini reale, deci discriminantul ei este negativ. Din a doua găsim

. Acestea sunt rădăcinile ecuației date.

O ecuație de formă se numește biquadratică

, Unde A ¹ 0. Ecuația biquadratică se rezolvă prin introducerea unei noi variabile: punând , ajungem la ecuația pătratică

. Ecuații iraționale.
Iraţional
este o ecuație în care variabila este conținută sub semnul rădăcinii sau sub semnul ridicării la o putere fracțională. O metodă de rezolvare a unor astfel de ecuații este metoda de ridicare a ambelor părți ale ecuației la aceeași putere:

A) transforma ecuația irațională dată în forma:

;

B) ridicăm ambele părți ale ecuației rezultate la

n- gradul:

;

B) având în vedere că

, obținem ecuația

f(x) = g(x);

)Rezolvăm ecuația și facem o verificare, deoarece ridicarea ambelor părți ale ecuației la o putere uniformă poate duce la apariția rădăcinilor străine. Această verificare se efectuează prin înlocuirea valorilor găsite ale variabilei în ecuația originală.

Utilizarea materialelor site-ului este posibilă sub rezerva unui link activ.