Gama de valori acceptabile (APV) ale logaritmului
Acum să vorbim despre restricții (ODZ - intervalul de valori admisibile ale variabilelor).
Ne amintim că, de exemplu, rădăcină pătrată nu poate fi extras din numere negative; sau dacă avem o fracție, atunci numitorul nu poate fi egal cu zero. Logaritmii au limitări similare:
Adică, atât argumentul, cât și baza trebuie să fie mai mari decât zero, dar baza nu poate fi încă egală.
De ce este așa?
Să începem cu un lucru simplu: să spunem asta. Atunci, de exemplu, numărul nu există, deoarece indiferent de puterea la care ridicăm, se dovedește întotdeauna. Mai mult, nu există pentru nimeni. Dar, în același timp, poate fi egal cu orice (din același motiv - este egal cu orice grad). Prin urmare, obiectul nu prezintă interes și a fost pur și simplu aruncat din matematică.
Avem o problemă similară în acest caz: la orice putere pozitivă este, dar nu poate fi ridicată deloc la o putere negativă, deoarece aceasta va duce la împărțirea cu zero (permiteți-mi să vă reamintesc asta).
Când ne confruntăm cu problema ridicării la o putere fracțională (care este reprezentată ca rădăcină: . De exemplu, (adică), dar nu există.
Prin urmare, este mai ușor să arunci motivele negative decât să le schimbi.
Ei bine, deoarece baza noastră a poate fi doar pozitivă, atunci indiferent de puterea la care o ridicăm, vom obține întotdeauna un număr strict pozitiv. Deci argumentul trebuie să fie pozitiv. De exemplu, nu există, deoarece nu va fi un număr negativ în nici un grad (sau chiar zero, prin urmare nici nu există).
În problemele cu logaritmii, primul lucru pe care trebuie să-l faceți este să scrieți ODZ. Hai sa-ti dau un exemplu:
Să rezolvăm ecuația.
Să ne amintim definiția: un logaritm este puterea la care trebuie ridicată baza pentru a obține un argument. Și după condiție, acest grad este egal cu: .
Primim cele obișnuite ecuație pătratică: . Să o rezolvăm folosind teorema lui Vieta: suma rădăcinilor este egală, iar produsul. Ușor de ridicat, acestea sunt numere și.
Dar dacă luați și scrieți imediat ambele numere în răspuns, puteți obține 0 puncte pentru problemă. De ce? Să ne gândim ce se întâmplă dacă înlocuim aceste rădăcini în ecuația inițială?
Acest lucru este în mod clar incorect, deoarece baza nu poate fi negativă, adică rădăcina este „terț”.
Pentru a evita astfel de capcane neplăcute, trebuie să notați ODZ chiar înainte de a începe să rezolvați ecuația:
Apoi, după ce am primit rădăcinile și, aruncăm imediat rădăcina și scriem răspunsul corect.
Exemplul 1(incearca sa rezolvi singur) :
Găsiți rădăcina ecuației. Dacă există mai multe rădăcini, indicați-l pe cea mai mică dintre ele în răspunsul dvs.
Soluţie:
În primul rând, să scriem ODZ:
Acum să ne amintim ce este un logaritm: la ce putere aveți nevoie pentru a ridica baza pentru a obține argumentul? La al doilea. Adică:
S-ar părea că rădăcina mai mică este egală. Dar nu este așa: conform ODZ, rădăcina este terță parte, adică nu este deloc o rădăcină ecuația dată. Astfel, ecuația are o singură rădăcină: .
Răspuns: .
Identitatea logaritmică de bază
Să ne amintim definiția logaritmului în formă generală:
Să înlocuim logaritmul în a doua egalitate:
Această egalitate se numește identitate logaritmică de bază. Deși, în esență, aceasta este egalitate - doar scrisă diferit definiția logaritmului:
Aceasta este puterea la care trebuie să o ridici pentru a ajunge.
De exemplu:
Rezolvați următoarele exemple:
Exemplul 2.
Găsiți sensul expresiei.
Soluţie:
Să ne amintim de regula din secțiune:, adică la ridicarea unei puteri la o putere, exponenții sunt înmulțiți. Să-l aplicăm:
Exemplul 3.
Demonstrează asta.
Soluţie:
Proprietățile logaritmilor
Din păcate, sarcinile nu sunt întotdeauna atât de simple - adesea trebuie mai întâi să simplificați expresia, să o aduceți la forma ei obișnuită și numai atunci va fi posibil să calculați valoarea. Acest lucru este cel mai ușor de făcut dacă știi proprietățile logaritmilor. Deci, să învățăm proprietățile de bază ale logaritmilor. Voi dovedi fiecare dintre ele, pentru că orice regulă este mai ușor de reținut dacă știi de unde vine.
Toate aceste proprietăți trebuie reținute fără ele, majoritatea problemelor cu logaritmii nu pot fi rezolvate.
Și acum despre toate proprietățile logaritmilor în detaliu.
Proprietatea 1:
Dovada:
Să fie atunci.
Avem: , etc.
Proprietatea 2: Suma logaritmilor
Suma logaritmilor cu aceleași baze este egală cu logaritmul produsului: .
Dovada:
Să fie atunci. Să fie atunci.
Exemplu: Găsiți sensul expresiei: .
Soluție: .
Formula pe care tocmai ai învățat-o ajută la simplificarea sumei logaritmilor, nu a diferenței, astfel încât acești logaritmi nu pot fi combinați imediat. Dar puteți face opusul - „împărțiți” primul logaritm în două: Și iată simplificarea promisă:
.
De ce este necesar acest lucru? Ei bine, de exemplu: cu ce este egal?
Acum este evident că.
Acum simplificați-l singur:
Sarcini:
Raspunsuri:
Proprietatea 3: Diferența de logaritmi:
Dovada:
Totul este exact la fel ca la punctul 2:
Să fie atunci.
Să fie atunci. Avem:
Exemplul din paragraful anterior devine acum și mai simplu:
Un exemplu mai complicat: . Îți poți da seama cum să o rezolvi singur?
Aici trebuie remarcat faptul că nu avem o singură formulă despre logaritmi la pătrat. Aceasta este ceva asemănător cu o expresie - nu poate fi simplificată imediat.
Prin urmare, să luăm o pauză de la formulele despre logaritmi și să ne gândim la ce fel de formule folosim cel mai des în matematică? Din clasa a VII-a!
Aceasta - . Trebuie să te obișnuiești cu faptul că sunt peste tot! Ele apar în probleme exponențiale, trigonometrice și iraționale. Prin urmare, ele trebuie amintite.
Dacă te uiți cu atenție la primii doi termeni, devine clar că acest lucru diferența de pătrate:
Răspuns pentru a verifica:
Simplificați-l singur.
Exemple
Răspunsuri.
Proprietatea 4: Scoaterea exponentului din argumentul logaritmului:
Dovada:Și aici folosim și definiția logaritmului: let, then. Avem: , etc.
Această regulă poate fi înțeleasă astfel:
Adică, gradul argumentului este mutat înaintea logaritmului ca coeficient.
Exemplu: Găsiți sensul expresiei.
Soluţie: .
Decideți singuri:
Exemple:
Raspunsuri:
Proprietatea 5: Luând exponentul de la baza logaritmului:
Dovada: Să fie atunci.
Avem: , etc.
Amintiți-vă: de la temeiuri gradul este exprimat ca opusul număr, spre deosebire de cazul precedent!
Proprietatea 6: Eliminarea exponentului din baza și argumentul logaritmului:
Sau dacă gradele sunt aceleași: .
Proprietatea 7: Tranziția la o nouă bază:
Dovada: Să fie atunci.
Avem: , etc.
Proprietatea 8: Schimbați baza și argumentul logaritmului:
Dovada: Acest caz special formulele 7: dacă înlocuim, obținem: , etc.
Să ne uităm la câteva exemple suplimentare.
Exemplul 4.
Găsiți sensul expresiei.
Folosim proprietatea logaritmilor nr. 2 - suma logaritmilor cu aceeași bază este egală cu logaritmul produsului:
Exemplul 5.
Găsiți sensul expresiei.
Soluţie:
Folosim proprietatea logaritmilor nr. 3 și nr. 4:
Exemplul 6.
Găsiți sensul expresiei.
Soluţie:
Să folosim proprietatea nr. 7 - treceți la baza 2:
Exemplul 7.
Găsiți sensul expresiei.
Soluţie:
Cum îți place articolul?
Dacă citiți aceste rânduri, atunci ați citit întreg articolul.
Și asta e tare!
Acum spune-ne cum ți se pare articolul?
Ai învățat cum să rezolvi logaritmii? Dacă nu, care este problema?
Scrie-ne în comentariile de mai jos.
Și, da, mult succes la examene.
Despre examenul unificat de stat și examenul unificat de stat și în viață în general
Logaritm număr pozitiv N la bază(b> 0, b 1 ) numit exponent x , la care trebuie să construiți b pentru a obține N .
Notație logaritmică:
Această intrare este echivalentă cu următoarele:b x = N .
EXEMPLE: jurnalul 3 81 = 4, deoarece 3 4 = 81;
Jurnal 1/3 27 = – 3, deoarece (1/3) - 3 = 3 3 = 27.
Definiția de mai sus a logaritmului poate fi scrisă ca o identitate:
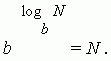
Proprietățile de bază ale logaritmilor.
1) jurnal b= 1 , deoarece b 1 = b.
b
2) jurnal 1 = 0 , deoarece b 0 = 1 .
b
3) Logaritmul produsului egal cu suma logaritmii factorilor:
jurnal( ab) = jurnal o+ jurnal b.
4) Logaritmul coeficientului este egal cu diferența dintre logaritmii dividendului și divizorului:
jurnal( o/b) = jurnal o– jurnal b.
5) Logaritmul unei puteri este egal cu produsul dintre exponent și logaritmul bazei sale:
jurnal (b k ) = k jurnal b.
Consecința acestei proprietăți este următoarea:logaritmul rădăcinii egal cu logaritmul numărului radical împărțit la puterea rădăcinii:

6) Dacă baza logaritmului este un grad, atunci valoarea inversul exponentului, poate fi scos din semnul log rima:

Ultimele două proprietăți pot fi combinate într-una singură:

7) Formula modulului de tranziție (de ex. e .trecerea de la o bază

logaritm la o altă bază): În cazul special când N=a

avem: Logaritm zecimal numit logaritm de bază 10. Este desemnat lg, adică jurnalul 10 = N lg, adică jurnalul 10lg. Logaritmii numerelor 10, 100, 1000, ... pnumerele sunt 1, 2, 3, ..., respectiv
aceste. au atât de multe pozitive unități, câte zerouri sunt într-un număr logaritmic după unu. Logaritmii numerelor 0,1, 0,01, 0,001, ... p –2, avna respectiv –1, –3, …, adică au atâtea negative câte zerouri sunt înaintea unu în numărul logaritmic ( numărare și zero numere întregi ). Logaritmi alte numere au o parte fracționară numită mantisa. Întregul o parte a logaritmului se numește caracteristică. Pentru utilizare practică
Logaritmii zecimali sunt cele mai convenabile.
Logaritm zecimal numit
Logaritmul naturale. Este desemnatlg, adică jurnalul 10
=
ln, adică jurnal lg, adică jurnalul 10 e ln.Număr e este irațional, asta(1 + 1
/
valoare aproximativă 2,718281828.)
valoare aproximativă 2,718281828. Eaeste limita la care tinde număruln cu spor nelimitat ).
n(cm.Logaritmul naturalprima limită minunată
Oricât de ciudat ar părea, logaritmii naturali s-au dovedit a fi foarte convenabil atunci când se efectuează diferite tipuri de operații legate de analiza funcțiilor.
Calcularea logaritmilor la bază
realizat mult mai rapid decât din orice alt motiv.
Deci, avem puteri de doi. Dacă luați numărul din linia de jos, puteți găsi cu ușurință puterea la care va trebui să ridicați doi pentru a obține acest număr. De exemplu, pentru a obține 16, trebuie să ridici doi la a patra putere. Și pentru a obține 64, trebuie să ridici doi la a șasea putere. Acest lucru se vede din tabel.
Și acum, de fapt, definiția logaritmului:
Operația de găsire a logaritmului unui număr la o bază dată se numește logaritmizare. Deci, să adăugăm o nouă linie la tabelul nostru:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
Din păcate, nu toți logaritmii se calculează atât de ușor. De exemplu, încercați să găsiți log 2 5. Numărul 5 nu este în tabel, dar logica dictează că logaritmul va fi undeva pe interval. Pentru că 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Astfel de numere se numesc iraționale: numerele de după virgulă pot fi scrise la infinit și nu se repetă niciodată. Dacă logaritmul se dovedește a fi irațional, este mai bine să îl lăsați așa: log 2 5, log 3 8, log 5 100.
Este important să înțelegem că un logaritm este o expresie cu două variabile (baza și argumentul). Mulți oameni confundă la început unde este baza și unde este argumentul. Pentru a evita neînțelegerile enervante, priviți imaginea:
În fața noastră nu este nimic altceva decât definiția unui logaritm. Amintiți-vă: logaritmul este o putere, în care trebuie construită baza pentru a obține un argument. Este baza care este ridicată la o putere - este evidențiată cu roșu în imagine. Se dovedește că baza este întotdeauna în jos! Le spun studenților mei această regulă minunată chiar de la prima lecție - și nu apare nicio confuzie.
Ne-am dat seama de definiție - tot ce mai rămâne este să înveți cum să numărăm logaritmii, de exemplu. scapă de semnul „bușten”. Pentru început, observăm că din definiție rezultă două fapte importante:
- Argumentul și baza trebuie să fie întotdeauna mai mari decât zero. Aceasta rezultă din definiția gradului indicator rațional, la care se reduce definiția unui logaritm.
- Baza trebuie să fie diferită de unul, deoarece unul în orice grad rămâne unul. Din această cauză, întrebarea „la ce putere trebuie ridicat cineva pentru a obține doi” este lipsită de sens. Nu există o astfel de diplomă!
Se numesc astfel de restricții intervalul de valori acceptabile(ODZ). Rezultă că ODZ a logaritmului arată astfel: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Rețineți că nu există restricții privind numărul b (valoarea logaritmului). De exemplu, logaritmul poate fi foarte negativ: log 2 0.5 = −1, deoarece 0,5 = 2 −1.
Totuși, acum luăm în considerare doar expresii numerice în care nu este necesar să cunoaștem VA logaritmului. Toate restricțiile au fost deja luate în considerare de către autorii sarcinilor. Dar când pleacă ecuații logaritmiceși inegalitățile, cerințele DHS vor deveni obligatorii. La urma urmei, baza și argumentul pot conține construcții foarte puternice care nu corespund neapărat restricțiilor de mai sus.
Acum să ne uităm la schema generală de calcul a logaritmilor. Acesta constă din trei etape:
- Exprimați baza a și argumentul x ca o putere cu baza minimă posibilă mai mare decât unu. Pe parcurs, este mai bine să scapi de zecimale;
- Rezolvați ecuația pentru variabila b: x = a b ;
- Numărul rezultat b va fi răspunsul.
Asta este! Dacă logaritmul se dovedește a fi irațional, acesta va fi vizibil deja în primul pas. Cerința ca baza să fie mai mare decât unu este foarte importantă: aceasta reduce probabilitatea de eroare și simplifică foarte mult calculele. La fel cu zecimale: dacă le convertiți imediat în cele obișnuite, vor fi mult mai puține erori.
Să vedem cum funcționează această schemă folosind exemple specifice:
Sarcină. Calculați logaritmul: log 5 25
- Să ne imaginăm baza și argumentul ca o putere a lui cinci: 5 = 5 1 ; 25 = 5 2 ;
- Să creăm și să rezolvăm ecuația:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - Am primit răspunsul: 2.
Sarcină. Calculați logaritmul:
Sarcină. Calculați logaritmul: log 4 64
- Să ne imaginăm baza și argumentul ca o putere a doi: 4 = 2 2 ; 64 = 2 6 ;
- Să creăm și să rezolvăm ecuația:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3; - Am primit răspunsul: 3.
Sarcină. Calculați logaritmul: log 16 1
- Să ne imaginăm baza și argumentul ca o putere a doi: 16 = 2 4 ; 1 = 2 0 ;
- Să creăm și să rezolvăm ecuația:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0; - Am primit raspunsul: 0.
Sarcină. Calculați logaritmul: log 7 14
- Să ne imaginăm baza și argumentul ca o putere a lui șapte: 7 = 7 1 ; 14 nu poate fi reprezentat ca o putere a șapte, deoarece 7 1< 14 < 7 2 ;
- Din paragraful anterior rezultă că logaritmul nu contează;
- Răspunsul este fără schimbare: log 7 14.
O mică notă despre ultimul exemplu. Cum poți fi sigur că un număr nu este o putere exactă a altui număr? Este foarte simplu - doar descompuneți-l în factori primi. Și dacă astfel de factori nu pot fi adunați în puteri cu aceiași exponenți, atunci numărul inițial nu este o putere exactă.
Sarcină. Aflați dacă numerele sunt puteri exacte: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 - grad exact, deoarece există un singur multiplicator;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nu este o putere exactă, întrucât există doi factori: 3 și 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - grad exact;
35 = 7 · 5 - din nou nu este o putere exactă;
14 = 7 · 2 - din nou nu este un grad exact;
Să remarcăm, de asemenea, că noi înșine numere prime sunt întotdeauna grade exacte ale lor.
Logaritm zecimal
Unii logaritmi sunt atât de comune încât au un nume și un simbol special.
Logaritmul zecimal al lui x este logaritmul la baza 10, adică. Puterea la care trebuie ridicat numărul 10 pentru a obține numărul x. Denumire: lg x.
De exemplu, log 10 = 1; lg 100 = 2; lg 1000 = 3 - etc.
De acum înainte, când o expresie precum „Găsiți lg 0.01” apare într-un manual, știți: aceasta nu este o greșeală de tipar. Acesta este un logaritm zecimal. Cu toate acestea, dacă nu sunteți familiarizat cu această notație, o puteți rescrie oricând:
log x = log 10 x
Tot ceea ce este adevărat pentru logaritmii obișnuiți este valabil și pentru logaritmii zecimali.
Logaritmul natural
Există un alt logaritm care are propria sa denumire. În unele privințe, este chiar mai important decât zecimală. Este vorba despre despre logaritmul natural.
Logaritmul natural al argumentului x este logaritmul la baza e, i.e. puterea la care trebuie ridicat numărul e pentru a obține numărul x. Denumire: ln x .
Mulți se vor întreba: care este numărul e? Acest număr irațional, valoarea sa exactă este imposibil de găsit și de notat. Voi da doar primele cifre:
e = 2,718281828459...
Nu vom intra în detaliu despre ce este acest număr și de ce este necesar. Nu uitați doar că e este baza logaritmului natural:
ln x = log e x
Astfel ln e = 1; ln e 2 = 2; ln e 16 = 16 - etc. Pe de altă parte, ln 2 este un număr irațional. În general, logaritmul natural al oricărui număr rațional este irațional. Cu excepția, desigur, pentru unitate: ln 1 = 0.
Pentru logaritmii naturali, toate regulile care sunt adevărate pentru logaritmii obișnuiți sunt valabile.
Proprietățile de bază ale logaritmului natural, grafic, domeniu de definiție, set de valori, formule de bază, derivată, integrală, expansiune în serie de putereşi reprezentarea funcţiei ln x folosind numere complexe.
ConţinutFuncția inversă
Inversa logaritmului natural este exponent.
Dacă, atunci
Dacă, atunci.
Derivată ln x
Derivată a logaritmului natural:
.
Derivată a logaritmului natural al modulului x:
.
Derivată de ordin al n-lea:
.
Derivarea formulelor > > >
Integral
Se calculează integrala integrare pe părți :
.
Aşa,
Expresii folosind numere complexe
Luați în considerare funcția variabilei complexe z:
.
Să exprimăm variabila complexă z prin modul rși argument φ
:
.
Folosind proprietățile logaritmului, avem:
.
Sau
.
Argumentul φ nu este definit în mod unic. Daca pui
, unde n este un număr întreg,
va fi același număr pentru n diferit.
Prin urmare, logaritmul natural, în funcție de o variabilă complexă, nu este o funcție cu o singură valoare.
Extinderea seriei de putere
Când are loc extinderea:
Literatura folosita:
ÎN. Bronstein, K.A. Semendyaev, Manual de matematică pentru ingineri și studenți, „Lan”, 2009.