При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.
- Виды проявления количественных связей между признаками
- функциональная связь
- корреляционная связь
- Определения функциональной и корреляционной связи
Функциональная связь - такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь - такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
- Практическое значение установления корреляционной связи
. Выявление причинно-следственной между факторными и
результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием
здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
- Величина, характеризующая направление и силу связи между признаками . Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1
- Способы представления корреляционной связи
- график (диаграмма рассеяния)
- коэффициент корреляции
- Направление корреляционной связи
- прямая
- oбратная
- Сила корреляционной связи
- сильная: ±0,7 до ±1
- средняя: ±0,3 до ±0,699
- слабая: 0 до ±0,299
- Методы определения коэффициента корреляции и формулы
- метод квадратов (метод Пирсона)
- ранговый метод (метод Спирмена)
- Методические требования к использованию коэффициента корреляции
- измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
- расчет может производиться с использованием абсолютных или производных величин
- для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
- число наблюдений не менее 30
- Рекомендации по применению метода ранговой корреляции (метод Спирмена)
- когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных
- когда признаки представлены не только количественными, но и атрибутивными значениями
- когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)
- Рекомендации к применению метода квадратов (метод Пирсона)
- когда требуется точное установление силы связи между признаками
- когда признаки имеют только количественное выражение
- Методика и порядок вычисления коэффициента корреляции
1) Метод квадратов
2) Ранговый метод
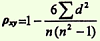
- Схема оценки корреляционной связи по коэффициенту корреляции
- Вычисление ошибки коэффициента корреляции

- Оценка достоверности коэффициента корреляции,полученного методом ранговой корреляции и методом квадратов
Способ 1
Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n - 2), где n - число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.
Способ 2
Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n - 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.
Задание: вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.
Таблица 1
Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.
Решение
.
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых
признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).
| Жесткость воды (в градусах) |
Количество кальция в воде (в мг/л) |
d х | d у | d х х d у | d x 2 | d y 2 |
| 4 8 11 27 34 37 |
28 56 77 191 241 262 |
-16 -12 -9 +7 +14 +16 |
-114 -86 -66 +48 +98 +120 |
1824 1032 594 336 1372 1920 |
256 144 81 49 196 256 |
12996 7396 4356 2304 9604 14400 |
| М х =Σ х / n | М у =Σ у / n | Σ d х x d у =7078 | Σ d х 2 =982 | Σ d y 2 =51056 | ||
| М х =120/6=20 | М y =852/6=142 | |||||
- Определить средние величины M x ряду вариант "х" и М у в ряду вариант "у" по формулам:
М х = Σх/n (графа 1) и
М у = Σу/n (графа 2) - Найти отклонение (d х и d у) каждой варианты от величины вычисленной средней в ряду "x" и в ряду "у"
d х = х - М х (графа 3) и d y = у - М у (графа4). - Найти произведение отклонений d x х d y и суммировать их: Σ d х х d у (графа 5)
- Каждое отклонение d x и d у возвести в квадрат и суммировать их значения по ряду "х" и по ряду "у": Σ d x 2 = 982 (графа 6) и Σ d y 2 = 51056 (графа 7).
- Определить произведение Σ d x 2 х Σ d y 2 и из этого произведения извлечь квадратный корень
- Полученные величины Σ (d x x d y) и √(Σd x 2 x Σd y 2) подставляем в формулу расчета коэффициента корреляции:
- Определить достоверность коэффициента корреляции:
1-й способ. Найти ошибку коэффициента корреляции (mr xy) и критерий t по формулам:
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.
2-й способ. Достоверность коэффициента корреляции оценивается по таблице "Стандартные коэффициенты корреляции" (см. приложение 1). При числе степеней свободы (n - 2)=6 - 2=4, наш расчетный коэффициент корреляции r xу = + 0,99 больше табличного (r табл = + 0,917 при р = 99%).
Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная : r ху = + 0,99, р > 99,9%).
на применение рангового методаЗадание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:
Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака "стаж работы в годах" имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод - метод квадратов.
Решение . Последовательность расчетов изложена в тексте, результаты представлены в табл. 2.
Таблица 2
Стаж работы в годах Число травм Порядковые номера (ранги) Разность рангов Квадрат разности рангов X Y d(х-у) d 2 До 1 года 24 1 5 -4 16 1-2 16 2 4 -2 4 3-4 12 3 2,5 +0,5 0,25 5-6 12 4 2,5 +1,5 2,25 7 и более 6 5 1 +4 16 Σ d 2 = 38,5 
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)
Число степеней свободы - 2 Уровень вероятности р (%) 95% 98% 99% 1 0,997 0,999 0,999 2 0,950 0,980 0,990 3 0,878 0,934 0,959 4 0,811 0,882 0,917 5 0,754 0,833 0,874 6 0,707 0,789 0,834 7 0,666 0,750 0,798 8 0,632 0,716 0,765 9 0,602 0,885 0,735 10 0,576 0,858 0,708 11 0,553 0,634 0,684 12 0,532 0,612 0,661 13 0,514 0,592 0,641 14 0,497 0,574 0,623 15 0,482 0,558 0,606 16 0,468 0,542 0,590 17 0,456 0,528 0,575 18 0,444 0,516 0,561 19 0,433 0,503 0,549 20 0,423 0,492 0,537 25 0,381 0,445 0,487 30 0,349 0,409 0,449 - Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464 с.
- Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. - М.: ГЭОТАР-МЕД, 2007. - 512 с.
- Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.
- Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). - СПб, 1998. -528 с.
- Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) - Москва, 2000. - 432 с.
- С. Гланц. Медико-биологическая статистика. Пер с англ. - М., Практика, 1998. - 459 с.
При изучении различных социально-экономических явлений выделяют функциональную связь и стохастическую зависимость. Функциональная связь - это такой вид связи, при которой некоторому взятому значению факторного показателя соответствует лишь одно значение результативного показателя. Функциональная связь проявляется во всех случаях исследования и для каждой определенной единицы анализируемой совокупности.
Размещено на www.сайт
В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:
Шкала Чеддока количественной оценки степени тесноты связи
Величина показателя тесноты связи
Характер связи
Практически отсутствует
Умеренная
При интерпретации значения коэффициента линейной корреляции по направлению связи выделяют прямую и обратную. В случае наличия прямой связи с повышением или снижением величины факторного признака происходит повышение или снижение показателей результативного признака, т.е. изменение фактора и результата происходит в одном направлении. Например, повышение величины прибыли способствует росту показателей рентабельности. При наличии обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с динамикой факторного признака. Например, с повышением производительности труда уменьшается себестоимость единицы выпускаемой продукции и т.п.
Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до –1. В случае полной положительной корреляции этот коэффициент равен плюс 1 (говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной), а при полной отрицательной – минус 1 (свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются).

 Пр1.:
Пр1.:
График зависимости застенчивости и дипресивности. Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны.

 Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)
Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)

 В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.
Используется две системы классификации корреляционных связей по их силе: общая и частная.
Общая классификация корреляционных связей:1) сильная, или тесная при коэффициенте корреляции r>0,70;2) средняя при 0,500,70, а не просто корреляция высокого уровня значимости.В следующей таблице написаны названия коэффициентов корреляции для различных типов шкал.
| Дихотомическая шкала (1/0) | Ранговая (порядковая) шкала | ||
| Дихотомическая шкала (1/0) | Коэфициент ассоциации Пирсона, коэффициент четырехклеточной сопряженности Пирсона. | Бисериальная корреляция | |
| Ранговая (порядковая) шкала | Рангово-бисериальная корреляция. | Ранговый коэффициент корреляции Спирмена или Кендалла. | |
| Интервальная и абсолютная шкала | Бисериальная корреляция | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент | Коэффициент корреляции Пирсона (коэффициент линейной корреляции) |
При r =0 линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общими средними, а линии регрессии параллельны осям координат.
Равенство r =0 говорит лишь об отсутствии линейной корреляционной зависимости (некоррелированности переменных), но не вообще об отсутствии корреляционной, а тем более, статистической зависимости.
Иногда вывод об отсутствии корреляции важнее наличия сильной корреляции. Нулевая корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует, при условии, что мы доверяем результатам измерений.
В SPSS: 11.3.2 Коэффициенты корреляции
До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения - большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.
В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена, а для переменных, принадлежащих к интервальной шкале - коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую.
Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav. При этом мы учтем, что дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:
· Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
· Перенесите переменную sex в список строк, а переменную psyche - в список столбцов.
· Щелкните на кнопке Statistics... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.
· В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.
Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:
/ СПСС 10
Задание № 10 Корреляционный анализ
Понятие корреляции
Корреляция или коэффициент корреляции – это статистический показательвероятностной связи между двумя переменными, измеренными по количественным шкалам. В отличие от функциональной связи, при которой каждому значению одной переменной соответствуетстрого определенное значение другой переменной,вероятностная связь характеризуется тем, что каждому значению одной переменной соответствуетмножество значений другой переменной, Примером вероятностной связи является связь между ростом и весом людей. Ясно, что один и тот же рост может быть у людей разного веса и наоборот.
Корреляция представляет собой величину, заключенную в пределах от -1 до + 1, и обозначается буквой r. Причем, если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой. Значение корреляции менее 0,2 рассматривается как слабая корреляция, свыше 0,5 – высокая. Если коэффициент корреляции отрицательный, это означает наличие обратной связи: чем выше значение одной переменной, тем ниже значение другой.
В зависимости от принимаемых значений коэффициента rможно выделить различные виды корреляции:
Строгая положительная корреляция определяется значениемr=1. Термин «строгая» означает, что значение одной переменной однозначно определяются значениями другой переменной, а термин «положительная» - что с возрастанием значений одной переменной значения другой переменной также возрастают.
Строгая корреляция является математической абстракцией и практически не встречается в реальных исследованиях.
Положительная корреляция соответствует значениям 0
Отсутствие корреляции определяется значениемr=0. Нулевой коэффициент корреляции говорит о том, что значения переменных никак не связаны между собой.
Отсутствие корреляции H o : 0 r xy =0 формулируется как отражениенулевой гипотезы в корреляционном анализе.
Отрицательная корреляция : -1
Строгая отрицательная корреляция определяется значениемr= -1. Она также, как и строгая положительная корреляция, является абстракцией и не находит выражение в практических исследованиях.
Таблица 1
Виды корреляции и их определения
Метод вычисления коэффициента корреляции зависит от вида шкалы, по которой измерены значения переменной.
Коэффициент корреляции r Пирсона является основным и может использоваться для переменных с номинальной и частично упорядоченными, интервальными шкалами, распределение значений по которым соответствует нормальному (корреляция моментов произведения). Коэффициент корреляции Пирсона дает достаточно точные результаты и в случаях анормальных распределений.
Для распределений, не являющихся нормальными, предпочтительнее пользоваться коэффициентами ранговой корреляции Спирмена и Кендалла. Ранговыми они являются потому, что программа предварительно ранжирует коррелируемые переменные.
Корреляцию rСпирмена программаSPSSвычисляет следующим образом: сначала переменные переводятся в ранги, а затем к рангам применяется формулаrПирсона.
В основе корреляции, предложенной М. Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между собой испытуемых. Если у пары испытываемых изменение по Х совпадают по направлению с изменением по Yсовпадает, то это свидетельствует о положительной связи. Если не совпадает – то об отрицательной связи. Данный коэффициент применяется преимущественно психологами, работающими с малыми выборками. Так как социологи работают с большими массивами данных, то перебор пар, выявление разности относительных частот и инверсий всех пар испытуемых в выборке затруднителен. Наиболее распространенным является коэф. Пирсона.
Поскольку коэффициент корреляции rПирсона является основным и может использоваться (с некоторой погрешностью в зависимости от типа шкалы и уровня анормальности в распределении) для всех переменных, измеренных по количественным шкалам, рассмотрим примеры его использования и сравним полученные результаты с результатами измерений по другим коэффициентам корреляции.
Формула вычисления коэффициента r - Пирсона:
r xy = ∑ (Xi-Xср)∙(Yi-Yср) / (N-1)∙σ x ∙σ y ∙
Где: Xi, Yi- Значения двух переменных;
Xср, Yср- средние значения двух переменных;
σ x , σ y – стандартные отклонения,
N- количество наблюдений.
Парные корреляции
Например, мы хотели бы выяснить, как соотносятся ответы между различными видами традиционных ценностей в представлениях студентов об идеальном месте работы (переменные: а9.1, а9.3, а9.5, а9.7), а затем о соотношении либеральных ценностях (а9.2, а9.4. а9.6, а9.8) . Данные переменные измерены по 5 – членным упорядоченным шкалам.
Используем процедуру: «Анализ», «Корреляции»,«Парные». По умолчанию коэф. Пирсона установлен в диалоговом окне. Используем коэф. Пирсона
В окно отбора переносятся тестируемые переменные: а9.1, а9.3, а9.5, а9.7
Путем нажатия ОК получаем расчет:
Корреляции
|
а9.1.т. Насколько важно иметь достаточно времени для семьи и личной жизни? |
Корреляция Пирсона |
||||
|
Знч.(2-сторон) |
|||||
|
а9.3.т. Насколько важно не бояться потерять свою работу? |
Корреляция Пирсона |
||||
|
Знч.(2-сторон) |
|||||
|
а9.5.т. Насколько важно иметь такого начальника, который будет советоваться с Вами, принимая то или иное решение? |
Корреляция Пирсона |
||||
|
Знч.(2-сторон) |
|||||
|
а9.7.т. Насколько важно работать в слаженном коллективе, ощущать себя его частью? |
Корреляция Пирсона |
||||
|
Знч.(2-сторон) |
|||||
** Корреляция значима на уровне 0.01 (2-сторон.).
Таблица количественных значений построенной корреляционной матрицы
Частные корреляции:
Для начала построим парную корреляцию между указанными двумя переменными:
|
Корреляции |
|||
|
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
Корреляция Пирсона |
||
|
Знч.(2-сторон) |
|||
|
с12. Ощущают близость со своей семьей |
Корреляция Пирсона |
||
|
Знч.(2-сторон) |
|||
|
**. Корреляция значима на уровне 0.01 (2-сторон.). |
|||
Затем используем процедуру построения частной корреляции: «Анализ», «Корреляции»,«Частные».
Предположим, что ценность «Важно самостоятельно определять и изменять порядок своей работы» во взаимосвязи с указанными переменными окажется тем решающим фактором, под влияние которого ранее выявленная связь исчезнет, либо окажется малозначимой.
|
Корреляции |
||||
|
Исключенные переменные |
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
с12. Ощущают близость со своей семьей |
||
|
с16. Ощущают близость с людьми, котрые имеют тот же достаток, что и вы |
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
Корреляция |
||
|
Значимость (2-сторон.) |
||||
|
с12. Ощущают близость со своей семьей |
Корреляция |
|||
|
Значимость (2-сторон.) |
||||
Как видно из таблицы под влиянием контрольной переменной связь несколько снизилась: с 0, 120 до 0, 102. Однако, это незначительно снижение не позволяет утверждать, что ране выявленная связь является отражением ложной корреляции, т.к. она остается достаточно высокой и позволяет с нулевой погрешностью опровергать нулевую гипотезу.
Коэффициент корреляции
Наиболее точный способ определения тесноты и характера корреляционной связи - нахождение коэффициента корреляции. Коэффициент корреляции есть число определяемое по формуле:


где r ху - коэффициент корреляции;
x i -значения первого признака;
у i -значения второго признака;
Средняя арифметическая значений первого признака
Средняя арифметическая значений второго признака
Для пользования формулой (32) построим таблицу, которая обеспечит необходимую последовательность в подготовке чисел для нахождения числителя и знаменателя коэффициента корреляции.
Как видно из формулы (32), последовательность действий такая: находим средние арифметические обоих признаков х и у, находим разность между значениями признака и его средней (х і - ) и у і - ), затем находим их произведение (х і - ) (у і - ) – суммa пocлeдних дает числитель коэффициента корреляции. Для нахождения его знаменателя следует разности (x i - )и (у і - ) возвести в квадрат, найти их суммы и извлечь корень квадратный из их произведения.
Так для примера 31 нахождение коэффициента корреляции в соответствии с формулой (32) можно представить следующим образом (табл. 50).
Полученное число коэффициента корреляции дает возможность установить наличие, тесноту и характер связи.
1. Если коэффициент корреляции равен нулю, связь между признаками отсутствует.
2. Если коэффициент корреляции равен единице, связь между признаками столь велика, что превращается в функциональную.
3. Абсолютная величина коэффициента корреляции не выходит за пределы интервала от нуля до единицы:
Это дает возможность ориентироваться на тесноту связи: чем величина коэффициента ближе к нулю, тем связь слабее, а чем ближе к единице, тем связь теснее.
4. Знак коэффициента корреляции «плюс» означает прямую корреляцию, знак «минус»-обратную.
Таблица50
| х і | у і | (х і - ) | (у і - ) | (х і - )(у і - ) | (х і - )2 | (у і - )2 |
| 14,00 | 12,10 | -1,70 | -2,30 | +3,91 | 2,89 | 5,29 |
| 14,20 | 13,80 | -1,50 | -0,60 | +0,90 | 2,25 | 0,36 |
| 14,90 | 14,20 | -0,80 | -0,20 | +0,16 | 0,64 | 0,04 |
| 15,40 | 13,00 | -0,30 | -1,40 | +0,42 | 0,09 | 1,96 |
| 16,00 | 14,60 | +0,30 | +0,20 | +0,06 | 0,09 | 0,04 |
| 17,20 | 15,90 | +1,50 | +2,25 | 2,25 | ||
| 18,10 | 17,40 | +2,40 | +2,00 | +4,80 | 5,76 | 4,00 |
| 109,80 | 101,00 | 12,50 | 13,97 | 13,94 |


Таким образом, вычисленный в примере 31 коэффициент корреляции r xy = +0,9. позволяет сделать такие выводы: существует корреляционная связь между величиной мышечной силы правой и левой кистей у исследуемых школьников (коэффициент r xy =+0,9 отличен от нуля), связь очень тесная (коэффициент r xy =+0,9 близок к единице), корреляция прямая (коэффициент r xy = +0,9 положителен), т. е. с увеличением мышечной силы одной из кистей увеличивается сила другой кисти.
При вычислении коэффициента корреляции и пользовании его свойствами следует учесть, что выводы дают корректные результаты в том случае, когда признаки распределены нормально и когда рассматривается взаимосвязь между большим количеством значений обоих признаков.
В рассмотренном примере 31 анализированы только 7 значений обоих признаков, что, конечно, недостаточно для подобных исследований. Напоминаем здесь еще раз, что примеры, в данной книге вообще и в этой главе в частности, носят характер иллюстрации методов, а не подробного изложения каких-либо научных экспериментов. Вследствие этого рассмотрено небольшое число значений признаков, измерения округлены - все это делается для того, чтобы громоздкими вычислениями не затемнять идею метода.
Особое внимание следует обратить на существо рассматриваемой взаимосвязи. Коэффициент корреляции не может привести к верным результатам исследования, если анализ взаимосвязи между признаками проводится формально. Возвратимся еще раз к примеру 31. Оба рассмотренных признака представляли собой значения мышечной силы правой и левой кистей. Представим себе, что под признаком x i в примере 31 (14,0; 14,2; 14,9... ...18,1) мы понимает длину случайно пойманных рыб в сантиметрах, а под признаком у і (12,1; 13,8; 14,2... ...17,4) -вес приборов в лаборатории в килограммах. Формально воспользовавшись аппаратом вычислений для нахождения коэффициента корреляции и получив в этом случае также r xy =+0>9, мы должны были заключить, что между длиной рыб и весом приборов существует тесная связь прямого характера. Бессмысленность такого вывода очевидна.
Чтобы избежать формального подхода к пользованию коэффициентом корреляции, следует любым другим методом - математическим, логическим, экспериментальным, теоретическим - выявить возможность существования корреляционной связи между признаками, то есть обнаружить органическое единство признаков. Только после этого можно приступать к пользованию корреляционным анализом и устанавливать величину и характер взаимосвязи.
В математической статистике существует еще понятие множественной корреляции - взаимосвязи между тремя и более признаками. В этих случаях пользуются коэффициентом множественной корреляции, состоящим из парных коэффициентов корреляции, описанных выше.
Например, коэффициент корреляции трех признаков-х і , у і , z і - есть:
где R xyz -коэффициент множественной корреляции, выражающий, как признак х i зависит от признаков у і и z i ;
r xy -коэффициент корреляции между признаками x i и y i ;
r xz -коэффициент корреляции между признаками Xi и Zi;
r yz - коэффициент корреляции между признаками y i , z i
Корреляционный анализ это:
Корреляционный анализКорреля́ция - статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи - например, для независимых случайных величин). Отрицательная корреляция - корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция - корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция - статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса - со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом .
Коэффициент корреляции
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике - это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X ,Y - две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

 ,
,
где cov обозначает ковариацию, а D - дисперсию, или, что то же самое,
,где символ обозначает математическое ожидание.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
- Неравенство Коши - Буняковского:
Корреляционный анализ
Корреляционный анализ - метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции ) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа - обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют . В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная , если одна переменная растёт, а вторая уменьшается, корреляция отрицательная .
Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = s i n (x ) и B = c o s (x ), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону s i n 2(x ) + c o s 2(x ) = 1.
Ограничения корреляционного анализа

 Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
- Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.
- Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных . Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
- Автокорреляционная функция
- Взаимнокорреляционная функция
- Ковариация
- Коэффициент детерминации
- Регрессионный анализ
Wikimedia Foundation. 2010.
Этап 3. Нахождение взаимосвязи между данными
Линейная корреляция
Последний этап задачи изучения связей между явлениями – оценка тесноты связи по показателям корреляционной связи. Этот этап очень важен для выявления зависимостей между факторными и результативными признаками, а следовательно, для возможности осуществления диагноза и прогноза изучаемого явления.
Диагноз (от греч. diagnosis распознавание) – определение существа и особенностей состояния какого-либо объекта или явления на основе его всестороннего исследования.
Прогноз (от греч. prognosis предвидение, предсказание) – всякое конкретное предсказание, суждение о состоянии какого-либо явления в будущем (прогноз погоды, исхода выборов и т.п.). Прогноз – это научно обоснованная гипотеза о вероятном будущем состоянии изучаемой системы, объекта или явления и характеризующие это состояние показатели. Прогнозирование – разработка прогноза, специальные научные исследования конкретных перспектив развития какого-либо явления.
Вспомним определение корреляции:
Корреляция – зависимость между случайными величинами, выражающаяся в том, что распределение одной величины зависит от значения другой величины.
Корреляционная связь наблюдается не только между количественными, но и качественными признаками. Существуют различные способы и показатели оценки тесноты связей. Мы остановимся лишь на линейном коэффициенте парной корреляции , который используется при наличии линейной связи между случайными величинами. На практике часто возникает необходимость определить уровень связи между случайными величинами неодинаковой размерности, поэтому желательно располагать какой-то безразмерной характеристикой этой связи. Такой характеристикой (мерой связи) является коэффициент линейной корреляции r xy , который определяется по формуле
где  ,
,  .
.
Обозначив и , можно получить следующее выражение для расчета коэффициента корреляции
 .
.
Если ввести понятие нормированного отклонения , которое выражает отклонение коррелируемых значений от среднего в долях среднего квадратического отклонения:
то выражение для коэффициента корреляции примет вид
![]() .
.
Если производить расчет коэффициента корреляции по итоговым значениям исходных случайных величин из расчетной таблицы, то коэффициент корреляции можно вычислить по формуле
 .
.
Свойства коэффициента линейной корреляции:
1). Коэффициент корреляции – безразмерная величина.
2). |r | £ 1 или .
3). , a,b = const, – величина коэффициента корреляции не изменится, если все значения случайных величин X и Y умножить (или разделить) на константу.
4). , a,b = const, – величина коэффициента корреляции не изменится, если все значения случайных величин X и Y увеличить (или уменьшить) на константу.
5). Между коэффициентом корреляции и коэффициентом регрессии существует связь:
Интерпретировать значения коэффициентов корреляции можно следующим образом:
Количественные критерии оценки тесноты связи:
В прогностических целях обычно используют величины с |r| > 0.7.
Коэффициент корреляции позволяет сделать вывод о существовании линейной зависимости между двумя случайными величинами, но не указывает, какая из величин обуславливает изменение другой. В действительности связь между двумя случайными величинами может существовать и без причинно-следственной связи между самими величинами, т.к. изменение обеих случайных величин может быть вызвано изменением (влиянием) третьей.
Коэффициент корреляции r xy является симметричным по отношению к рассматриваемым случайным величинам X и Y . Это означает, что для определения коэффициента корреляции совершенно безразлично, какая из величин является независимой, а какая – зависимой.
Значимость коэффициента корреляции
Даже для независимых величин коэффициент корреляции может оказаться отличным от нуля вследствие случайного рассеяния результатов измерений или вследствие небольшой выборки случайных величин. Поэтому следует проверять значимость коэффициента корреляции.
Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента :
 .
.
Если t > t кр (P, n -2), то линейный коэффициент корреляции значим, а следовательно, значима и статистическая связь X и Y .
 .
.
Для удобства вычислений созданы таблицы значений доверительных границ коэффициентов корреляции для различного числа степеней свободы f = n –2 (двусторонний критерий) и различных уровней значимости a = 0,1; 0,05; 0,01 и 0,001. Считается, что корреляция значима, если рассчитанный коэффициент корреляции превосходит значение доверительной границы коэффициента корреляции для заданных f и a .
Для больших n и a = 0,01 значение доверительной границы коэффициента корреляции можно вычислить по приближенной формуле
![]() .
.
При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.
Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.
До сих пор при анализе результатов нашего опыта по изучению действия марихуаны мы сознательно игнорировали такой показатель, как время реакции. Между тем было бы интересно проверить, существует ли связь между эффективностью реакций и их быстротой. Это позволило бы, например, утверждать, что чем человек медлительнее, тем точнее и эффективнее будут его действия и наоборот.
С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве - Пирсона (r) и вычисление коэффициента корреляции рангов Спирмена (r s ), который применяется к порядковым данным, т. е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции.
Коэффициент корреляции
Коэффициент корреляции - это величина, которая может варьировать в пределах от -1 до 1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:
Переменная

В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:

В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n -2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных ( = п - 2 = 6) при вычислении r (табл. В.4) и 7 пар данных ( = п - 2 = 5) при вычислении r s (табл. 5 в дополнении Б. 5).
Коэффициент Браве – Пирсона
Для вычисления этого коэффициента применяют следующую формулу (у разных авторов она может выглядеть по-разному):

где XY - сумма произведений данных из каждой пары;
n - число пар;
- средняя для данных переменной X ;
Средняя для данных переменной Y ;
S Х - x ;
s Y - стандартное отклонение для распределения у.
Теперь мы можем использовать этот коэффициент для того, чтобы установить, существует ли связь между временем реакции испытуемых и эффективностью их действий. Возьмем, например, фоновый уровень контрольной группы.

n = 15 15,8 13,4 = 3175,8;
(n – 1)S x S y = 14 3,07 2,29 = 98,42;
r
=

Отрицательное значение коэффициента корреляции может означать, что чем больше время реакции, тем ниже эффективность. Однако величина его слишком мала для того, чтобы можно было говорить о достоверной связи между этим двумя переменными.
nXY= ………
(n - 1)S X S Y = ……
Какой вывод можно сделать из этих результатов? Если вы считаете, что между переменными есть связь, то какова она - прямая или обратная? Достоверна ли она [см. табл. 4 (в дополнении Б. 5) с критическими значениями r ]?
Коэффициент корреляции рангов Спирмена r s
Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании r. Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами.
Дело в том, что при использовании коэффициента корреляции рангов Спирмена (r s ) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» студенты при прохождении ими как психологии, так и математики, или даже при двух разных преподавателях психологии?). Если коэффициент близок к + 1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к - 1, можно говорить о полной обратной зависимости.
Коэффициент r s вычисляют по формуле

где d- разность между рангами сопряженных значений признаков (независимо от ее знака), а n -число пар.
Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент r (в этих случаях бывает необходимо превратить количественные данные в порядковые).
Поскольку именно так обстоит дело с распределением значений эффективности и времени реакции в экспериментальной группе после воздействия, можно повторить расчеты, которые вы уже проделали для этой группы, только теперь не для коэффициента r , а для показателя r s . Это позволит посмотреть, насколько различаются эти два показателя*.

* Следует помнить, что
1) для числа попаданий 1-й ранг соответствует самой высокой, а 15-й-самой низкой результативности, тогда как для времени реакции 1-й ранг соответствует самому короткому времени, а 15-й-самому долгому;
2) данным ex aequo придается средний ранг.

Таким образом, как и в случае коэффициента r, получен положительный, хотя и недостоверный, результат. Какой же из двух результатов правдоподобнее: r = -0,48 или r s = +0,24? Такой вопрос может встать лишь в том случае, если результаты достоверны.
Хотелось бы еще раз подчеркнуть, что сущность этих двух коэффициентов несколько различна. Отрицательный коэффициент r указывает на то, что эффективность чаще всего тем выше, чем время реакции меньше, тогда как при вычислении коэффициента r s требовалось проверить, всегда ли более быстрые испытуемые реагируют более точно, а более медленные - менее точно.
Поскольку в экспериментальной группе после воздействия был получен коэффициент r s , равный 0,24, подобная тенденция здесь, очевидно, не прослеживается. Попробуйте самостоятельно разобраться в данных для контрольной группы после воздействия, зная, что d 2 = 122,5:
; достоверно ли?
Каков ваш вывод?………………………………… ……………………………………………………………
…………………………………………………………………………………………………………………….
Итак, мы рассмотрели различные параметрические и непараметрические статистические методы, используемые в психологии. Наш обзор был весьма поверхностным, и главная задача его заключалась в том, чтобы читатель понял, что статистика не так страшна, как кажется, и требует в основном здравого смысла. Напоминаем, что данные «опыта», с которыми мы здесь имели дело, - вымышленные и не могут служить основанием для каких-либо выводов. Впрочем, подобный эксперимент стоило бы действительно провести. Поскольку для этого опыта была выбрана сугубо классическая методика, такой же статистический анализ можно было бы использовать во множестве различных экспериментов. В любом случае нам кажется, что мы наметили какие-то главные направления, которые могут оказаться полезны тем, кто не знает, с чего начать статистический анализ полученных результатов.
Существуют три главных раздела статистики: описательная статистика, индуктивная статистика и корреляционный анализ.




