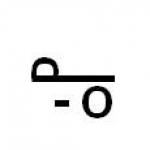GRAPHIC WORK
Subject:COMPLEX DRAWING OF A GROUP OF GEOMETRIC BODIES
Goals: acquire practical skills in performing a complex drawing of a group geometric bodies, learn to competently and accurately execute drawings, develop spatial concepts.
EXERCISE: build a group of geometric bodies on A3 format in three projections, mutual arrangement which are presented in horizontal projection and isometric projection (according to options).
Each object, from the point of view of spatial form, is either a geometric body or a combination of various geometric bodies limited by curved or flat surfaces. To correctly draw a drawing of an object, you must be able to draw drawings of individual geometric bodies.
To develop spatial imagination, it is useful to make complex drawings of a group of geometric bodies and simple models from nature. A visual representation of a group of geometric bodies is shown in Fig. 1.
The construction of a complex drawing of this group of geometric bodies should begin with a horizontal projection, since the bases of the cylinder, cone and hexagonal pyramid are projected onto the horizontal projection plane without distortion. Using vertical communication lines we build a frontal projection. We build a profile projection using vertical and horizontal communication lines.
Rice. 1
Execution Sequence graphic work
We begin the construction of geometric bodies from a top view, the relative position of which is presented in a horizontal projection and an isometric projection (in the version shown in the drawing above). Then, using vertical communication lines, we obtain a frontal projection, and construct a profile projection using vertical and horizontal communication lines. Next, in the remaining space we build an axonometry of these geometric bodies.
Projection of cylinders. The simplest is to construct orthogonal projections of a right circular cylinder with a vertical axis.
Side surface The cylinder is formed by the movement of generatrix AB around its axis along the guide circle of its base. In Fig. 1a it is given visual image this cylinder. Figure 2b shows the sequence of constructing its three projections - horizontal, frontal, profile. To simplify the construction of the base of the cylinder, it is assumed to be located on the horizontal projection plane - H.
a) b)
Rice. 2
The construction begins with an image of the base of the cylinder, i.e. two projections of a circle (Fig.2b ). Since the circle is located on the H plane, its horizontal projection will be identical to the circle itself; the frontal and profile projection of this circle is a segment of a horizontal straight line of length. Equal to diameter base circumference. After constructing the base, we will draw two contour (outline) generatrices on the front and profile and plot the height of the cylinder on them. Next, we will draw a segment of the horizontal straight line, which is the frontal projection and the profile projection of the upper base of the cylinder. The horizontal projections of the upper and lower bases of the cylinder coincide (merge).
Projection of cones. Visual representation of direct circular cone shown in Fig. 3a. The lateral surface of this cone is formed by the movement of the generatrixS.B.near the axis of the cone along the guide - the circumference of the base.
a) b)
Rice. 3
The construction begins with an image of the base of the cone (Fig. 3b). Since the circle is located on the H plane, its horizontal projection will be identical to the circle itself; the frontal and profile projection of this circle is a segment of a horizontal straight line of length. Equal to the diameter of the base circle. After constructing the base on the frontal projection and the profile from the middle, we set aside the height of the cone (Fig. 3b). We connect the resulting vertex of the cone with straight lines to the ends of the frontal projection of the base and the profile projection of the base.
Projection of the pyramids. The construction of three projections of a hexagonal pyramid (Fig. 4a) resembles the construction of the previous figures.
a) b)
Rice. 4
We begin the construction from the base of the pyramid - regular hexagonal (Fig. 4b). It can be constructed using a compass by dividing the circle into six equal parts. Then, using vertical communication lines, we obtain the frontal and profile projections of the base and from their middle we restore the perpendicular and plot the height of the pyramid on it. We get the top. We connect the vertex by straight lines, which are the frontal projections of the ribs, with the vertices of the corners of the hexagon (the profile projections of the three rear ribs coincide).
Projection of a straight pentagonal prism. The construction of three projections of a straight pentagonal prism (Fig. 5a) also resembles the construction of the previous figures.
a) b)
Rice. 5
We begin the construction from the base of the prism - a regular pentagon (Fig. 5b). It can be constructed using a compass by dividing the circle into five equal parts. Then, using vertical communication lines, we obtain a frontal projection, where we depict five edges, two of which are invisible, and a profile projection, where three vertical edges are depicted. We get the top. As with the projections of a cylinder, the horizontal projections of the upper and lower bases coincide.
Options for tasks.
Summarizing, Homework
Literature:
Brodsky A.M. Engineering graphics (metalworking): textbook for secondary vocational education - M. "Academy", 2008
Brodsky A.M. Workshop on engineering graphics: tutorial for secondary vocational education - M. "Academy", 2008
Kuprikov M.Yu. Engineering graphics: Textbook for secondary vocational education – M. “Drofa”, 2010
Bogolyubov S.N. Assignments for the drawing course. – M., Higher. school, 2008
– State Public Scientific and Technical Library of Russia.
Subject:“Construction of an isometric projection of a group of geometric bodies according to description.”
Let's look at an example.
Construct an isometric projection of a group of geometric bodies: cuboid(with dimensions length 90 mm, width 50 mm and height 30 mm) is located on its larger edge. A straight circular cone is installed in the center of the second larger face (base diameter 70 mm, height 80 mm). On the side of the smaller face there is a regular triangular prism (the trigon is inscribed in a circle with a diameter of 40 mm, the height of the prism is 30 mm).
Algorithm for completing the task.
Before proceeding with an isometric projection, it is necessary to imagine possible options for the location of a group of bodies in order to correctly layout the drawing.
First, let's imagine each body separately:
So, a rectangular parallelepiped and possible options for its location:
rice. 2
rice. 3
Which option is right for us, based on the conditions of the problem?
In our case, based on the conditions of the task, the preferred option for the arrangement of the parallelepiped, made on rice. 1a. But it must be taken into account that Fig.1a the length of the parallelepiped is parallel to the X axis, but it can also be parallel to the Y axis (Fig. 1b).
Now let’s imagine a straight circular cone; according to the conditions of the problem, it can only be located vertically ( rice. 4), because installed on the second large face of the parallelepiped ( Fig.4), which is located in the XY plane. A regular triangular prism is installed on the smaller face of the parallelepiped.
Which of the presented options corresponds to the conditions of the problem?
Projection of regular triangular and hexagonal prisms. The bases of the prisms, parallel to the horizontal projection plane, are depicted on it in full size, and on the frontal and profile planes - as straight segments. The side faces are depicted without distortion on those projection planes to which they are parallel, and in the form of straight segments on those to which they are perpendicular (Fig. 78). Edges. inclined to the projection planes are depicted distorted on them. Fig 78. Prisms: a. g - projection; b, d - drawings in a system of rectangular projections: c, c - isometric projections The dimensions of the prisms are determined by their height and the dimensions of the base figure. The dash-dot lines in the drawing indicate the axes of symmetry. The construction of isometric projections of the prism begins from the base. Then perpendiculars are drawn from each vertex of the base, on which segments are laid, equal to height, and straight lines parallel to the edges of the base are drawn through the obtained points. A drawing in a system of rectangular projections also begins with a horizontal projection. Projection of a regular quadrangular pyramid. The square base of the pyramid is projected onto the horizontal plane H in full size. On it, diagonals depict the lateral ribs running from the tops of the base to the top of the pyramid (Fig. 79).Let's look carefully at Fig.1a. The smaller face of the parallelepiped is located in the ZY plane ( Fig.1a), therefore, the base of a regular triangular prism should also be located in the ZY plane. Thus, the prism must be positioned in accordance with rice. 5 B.
Which of the presented options is preferable? Why?
Case on rice. 6b preferable. The axes in isometry must be placed closer to the right edge of the sheet. Taking into account the dimensions of the rectangular parallelepiped, to locate the center of the coordinate axes, it is necessary to move 60 mm from the right edge of the sheet to the left, and 100 mm upward from the bottom edge of the sheet.
Step-by-step construction of a group of geometric bodies
When determining the center of a face, it is advisable not to draw diagonals completely, so as not to load the drawing with unnecessary construction lines; in subsequent drawings, the center of the face will be marked only by strokes from the diagonals, and we will also remove the auxiliary lines for constructing the axes.
In order not to overload the drawing, to indicate the center of the face, we will leave only two strokes from the diagonals. Let's construct a drawing of a trigon (regular triangle) according to the conditions of the problem and introduce the ZY axis, since the base of the prism is located on the smaller face, which in turn is parallel to the ZY plane.
Do not erase the construction lines!
Homework
Construct an isometric projection of a group of geometric bodies: a rectangular parallelepiped (with dimensions length 70 mm, width 50 mm and height 20 mm) is located on its middle face. A straight circular cylinder (base diameter 50 mm, height 65 mm) is installed in the center of the larger face. On the side of the other middle face there is a regular hexagonal pyramid. A hexagon (regular hexagon) is inscribed in a circle with a diameter of 50 mm, the height of the pyramid is 65 mm.
Rice. 79. Pyramid: projection: b drawing in a system of rectangular projections; in isometric projection Frontal and profile projections of the pyramid are isosceles triangles. The dimensions of the pyramid are determined by the length b of the two sides of its base and the height h. The isometric projection of the pyramid begins to be built from the base. A perpendicular is drawn from the center of the resulting figure, the height of the pyramid is plotted on it and the resulting point is connected to the vertices of the base. Projection of a cylinder and a cone. If the circles lying at the bases of the cylinder and cone are located parallel to the horizontal plane H, their projections onto this plane will also be circles (Fig. 80, b and d). 
Rice. 80. Cylinder and cone: a, d - projection; b, d drawings in a system of rectangular projections; V. e - isometric projections The frontal and profile projections of the cylinder in this case are rectangles, and the cones are isosceles triangles. Please note that on all projections the axes of symmetry should be drawn, with which the drawings of the cylinder and cone begin. The frontal and profile projections of the cylinder are the same. The same can be said about cone projections. Therefore, in this case, profile projections in the drawing are unnecessary. In addition, thanks to the “diameter” icon, you can imagine the shape of a cylinder from one projection (Fig. 81). It follows that in such cases there is no need for three projections. 
Rice. 81. Image of a cylinder in one view The dimensions of the cylinder and cone are determined by their height h and base diameter d. The methods for constructing an isometric projection of a cylinder and a cone are the same. To do this, draw the x and y axes, on which a rhombus is built. Its sides are equal to the diameter of the base of the cylinder or cone. An oval is inscribed in the rhombus (see Fig. 66). Projections of a group of geometric bodies. Figure 83 shows the projections of a group of geometric bodies. Can you tell how many geometric bodies are included in this group? What kind of bodies are these? 
Rice. 83. Drawing of a group of geometric bodies Having examined the images, it can be established that it contains a cone, a cylinder and a rectangular parallelepiped. They are located differently relative to the projection planes and each other. How exactly? The axis of the cone is perpendicular to the horizontal plane of projections, and the axis of the cylinder is perpendicular to the profile plane of projections. Two faces of the parallelepiped are parallel to the horizontal projection plane. On a profile projection, the image of a cylinder is to the right of the image of a parallelepiped, and on a horizontal projection it is below. This means that the cylinder is located in front of the parallelepiped, therefore part of the parallelepiped in the front projection is shown by a dashed line. From horizontal and profile projections it can be established that the cylinder touches the parallelepiped. The frontal projection of the cone touches the projection of the parallelepiped. However, judging by the horizontal projection, the parallelepiped does not touch the cone. The cone is located to the left of the cylinder and parallelepiped. In profile projection, it partially covers them. Therefore, invisible sections of the cylinder and parallelepiped are shown with dashed lines. How will the profile projection in Figure 83 change if a cone is removed from the group of geometric bodies? Entertaining tasks
1. There are checkers on the table, as shown in Figure 84, a. Based on the drawing, count how many checkers are in the first columns closest to you. How many checkers are there on the table? If you find it difficult to count them according to the drawing, try first stacking the checkers in columns using the drawing. Now try to answer the questions correctly. 
Rice. 84. Exercises 2. Checkers are arranged in four columns on the table. In the drawing they are shown in two projections (Fig. 84, b). How many checkers are on the table if there are equal numbers of black and white? To solve this problem, you need not only to know the rules of projection, but also to be able to reason logically. Geometric bodies can be depicted in a system of three mutually perpendicular projection planes and on one plane (axonometric projection).
The contours of geometric bodies in any images are specified by the projections of their vertices, edges, generators, faces and bases. Thus, the construction of projections of geometric bodies is reduced to the construction of projections of points, lines and flat figures.
For various constructions on geometric bodies, it is convenient to use a rectangular coordinate system associated directly with the body. Typically, the coordinate planes of such a system are combined with the planes of symmetry of the body and the coordinate axes are indicated on the projections (Fig. 90).
When constructing a point or line on the surface of a geometric body, it is first set on one projection and it is assumed that it is visible (for example, in Fig. 90 the point A specified on a horizontal projection). Then, on all projections, an image of the surface on which the point (line) is located is found, and its missing projections are constructed.
To construct axonometric projections of points located on the surface of the body, in a system of three projection planes, the coordinates of the point are determined relative to the selected coordinate system and sequentially plotted on the axonometric axes or parallel to them.
To construct an axonometric projection of a point belonging to the level plane, it is enough to determine its coordinates in this plane.
For example, an isometric projection of a point A(Fig. 91), located on the profile plane (the front base of the prism), is built according to its coordinates - at A And z A .
Axonometric projections of points lying on the faces of the projecting or general position are constructed using auxiliary lines that are drawn on the faces through given points. The auxiliary line gives the image of a point greater clarity, since it clearly establishes that it belongs to a specific face.
In Fig. 91 constructed isometric projection of a point IN, located on the profile projecting plane (side face of the prism). First, they are laid out along the axis Y from point O coordinate at B and through its end draw a straight line parallel to the Z axis. At the intersection of this straight line with the edge of the base of the prism, a point is obtained whose height is equal to the coordinate z V. Through this point a straight line parallel to the axis is drawn in the plane of the side face X, and the coordinate is plotted on it x V.
An example of a point lying on a face occupying general position, serves as a point A(Fig. 92). It is constructed in dimetric projection on the auxiliary line SB, drawn through the indicated point on the edge of the pyramid.
To construct a dimetric projection of a straight line S.B. along the axis X set aside the coordinate x B and through its end draw a straight line parallel to the axis Y. At its intersection with the edge of the base, a point is obtained IN and conduct a direct SB. Next, by connecting points B and O, a dimetric projection is obtained right triangle SOB, and start constructing a point A. To do this, the coordinate is plotted along the Z axis z A and through this end a straight line parallel to the leg is drawn OB, and continue it until it intersects with the hypotenuse S.B. at the point A.
Axonometric projections of points located on a cylindrical surface are constructed using the generators of the cylinder.
Through a given point, for example A, draw a generatrix (Fig. 93) and construct its dimetric projection according to the coordinates x A And at A. Then, from the base of the cylinder on this generatrix, the coordinate is plotted z A and get the point A.
To construct axonometric projections of points lying on the surface of a cone, its generators are also used.
For example, to construct an isometric projection of a point A(Fig. 94) the generatrix is used SB. The sequence of constructing an isometric projection of a point A is similar to constructing a dimetric projection of the point of the same name in Fig. 92.
To transfer points or lines from projections to a development, it is necessary to mark edges (for polyhedra) or generators (for bodies of rotation) in both images in order to correctly place the given points (segments) on the development.
In Fig. 95 shows the transfer of a broken line 1 - 2 - 3 - 4, located on the side surface of a hexagonal pyramid, from projections onto the scan. Points 1, 4 And 2 lie on the edges of the pyramid, which are projected without distortion onto the plane H(ribs A.F. And Sun) or V(edge SA). Therefore, segments are measured on a horizontal projection L 1 =a1 And L 4 = c4, and on the front - a segment L 2 = s"2" and transfer them to the corresponding development edges. Dot 3 lies on the edge SB, occupying a general position. To determine the length of a segment L 3 edge S.B. along with the dot 3 rotated around the height of the pyramid to a position parallel to the plane V, that is, until it aligns with the edge SD(or SA). Then the segment is measured on the frontal projection L 3 = s"3 1 and transfer it to the scanner.
If the point is located on the face of a polyhedron or on the lateral surface of a body of rotation, then it is constructed on the development using the auxiliary line that was used to construct the projections of the point.
For example, dot A(Fig. 96), belonging to the conical surface, is depicted on the generatrix on the projection and development SB. First, a generatrix is built on the development S.B. using a chord L B. Then turn the point A around the axis of the cone until it is aligned on the frontal projection with the contour line of the cone. Next, measure the length of the segment L A= s"a 1 and, putting it aside on the generatrix SB, get an image of a point A on the scan.
When training to read the projections of a geometric body, i.e., to represent its shape as a whole by projections and the ability to see its individual elements on any projection: points, lines (straight lines,
arcs, pattern curves), flat figures, it is recommended to highlight the required elements of geometric bodies with colored pencils. In this case it should
distinguish between projections of visible and invisible elements. The designation of projections of invisible points is enclosed in brackets, and invisible
lines are shown as dashed lines.
 | Rice. 98 |
 | Rice. 99 |
Task 20. Geometric bodies. Construct two given geometric bodies in a system of three projection planes and in an isometric projection, as well as their development, and determine the projections on all images given points and lines.
In order to imagine the shape of a part when making drawings, it is convenient to mentally dissect the part into geometric bodies. Geometric bodies bounded by flat figures - polygons - are called polyhedra (Fig. 13). Their flat figures are called faces, and the lines of their intersection are called edges. An angle formed by faces converging at one point - a vertex - will be a polyhedral angle. For example. Prism and pyramid are polyhedra. Bodies of revolution are limited by surfaces that are obtained as a result of rotation about the axis of some line AB, called the generatrix.
Rice. 13. Polyhedral bodies and bodies of revolution
Prism projections
Constructing a projection of a regular straight hexagonal prism (Fig. 14) begins with making its horizontal projection - a regular hexagon. From the vertices of this hexagon, vertical communication lines are drawn and a frontal projection of the lower base of the prism is constructed. This projection is represented by a horizontal line segment. From this straight line upward, the height of the prism is plotted and a frontal projection of the upper base is constructed. Then the frontal projections of the ribs are drawn - segments of vertical straight lines equal to the height of the prism. The frontal projections of the anterior and posterior ribs coincide. Horizontal projections of the side faces are depicted as straight segments.
Rice. 14. Projection of a hexagonal prism
Pyramid projections
The construction of projections of a trihedral pyramid begins with the construction of a base, the horizontal projection of which represents the actual appearance of the triangle (Fig. 15). The frontal projection of the base is depicted by a horizontal straight line segment. From the horizontal projection s of the vertex of the pyramid, the frontal projection s’ of the vertex is obtained. By connecting point s’ with points 1’, 2’ and 3’, frontal projections of the edges of the pyramid are obtained.
Horizontal projections of the ribs are obtained by connecting the horizontal projection s of the top of the pyramid with the horizontal projections of the 1st, 2nd and 3rd vertices of the base.
Rice. 15. Pyramid projections
Cylinder projections
The lateral surface of a right circular cylinder is formed by the movement of a segment AB around a vertical axis along a guide circle. In Fig. 16, and a visual image of the cylinder is given. The construction of horizontal and frontal projections of the cylinder is shown in Fig. 16, b and 16, c.
Rice. 16. Projections of a cylinder
The construction begins with an image of the base of the cylinder, i.e. two projections of a circle. Because If the circle is located on the H plane, then it is projected onto this plane without distortion. The frontal projection of a circle is a segment of a horizontal straight line equal to the diameter of the base circle.
After constructing the base, two outline (extreme) generators are drawn on the frontal projection and the height of the cylinder is plotted on them. Draw a segment of a horizontal straight line, which is the frontal projection of the upper base of the cylinder.
Projections of cones.
A visual representation of a right circular cone is shown in Fig. 17, a. The lateral surface of the cone is formed by rotation of the generatrix BS about the axis of the cone along a guide - the circle of the base. The sequence of constructing two projections of a cone is shown in Fig. 17, b and c. Two projections of the base are preliminarily constructed. The horizontal projection of the base is a circle. If we assume that the base of the cone lies on the H plane, then the frontal projection will be a straight segment equal to the diameter of this circle. On the frontal projection, a perpendicular is restored from the middle of the base and the height of the cone is plotted on it. The resulting frontal projection of the top of the cone is connected by straight lines to the ends of the frontal projection of the base and a frontal projection of the cone is obtained.
Rice. 17. Projections of a cone
