ম্যাট্রিক্স র‍্যাঙ্ক 2x2। একটি ম্যাট্রিক্সের র্যাঙ্ক খোঁজা। একটি ম্যাট্রিক্সের র্যাঙ্ক নির্ধারণ করা

r সংখ্যাটিকে ম্যাট্রিক্স A এর র্যাঙ্ক বলা হয় যদি:
1) ম্যাট্রিক্স A-তে r অর্ডারের একটি অ-শূন্য মাইনর রয়েছে;
2) অর্ডারের সমস্ত অপ্রাপ্তবয়স্ক (r + 1) এবং উচ্চতর, যদি তারা বিদ্যমান থাকে, তাহলে শূন্যের সমান।
অন্যথায়, একটি ম্যাট্রিক্সের র্যাঙ্ক হল একটি অ-শূন্য নাবালকের সর্বোচ্চ ক্রম।
পদবি: রংএ, আর এ বা আর।
এটি সংজ্ঞা থেকে অনুসরণ করে যে r একটি ধনাত্মক পূর্ণসংখ্যা। একটি নাল ম্যাট্রিক্সের জন্য, র্যাঙ্কটি শূন্য বলে বিবেচিত হয়।

সার্ভিস অ্যাসাইনমেন্ট. অনলাইন ক্যালকুলেটরটি খুঁজে বের করার জন্য ডিজাইন করা হয়েছে ম্যাট্রিক্স র‌্যাঙ্ক. সমাধানটি ওয়ার্ড এবং এক্সেল ফরম্যাটে সংরক্ষণ করা হয়েছে। সমাধান উদাহরণ দেখুন।

নির্দেশ. ম্যাট্রিক্সের মাত্রা নির্বাচন করুন, পরবর্তী ক্লিক করুন।

সংজ্ঞা। র্যাঙ্কের একটি ম্যাট্রিক্স দেওয়া যাক। শূন্য এবং ক্রম r ছাড়া অন্য যেকোন ম্যাট্রিক্স মাইনরকে মৌলিক বলা হয় এবং এর উপাদানগুলির সারি এবং কলামগুলিকে মৌলিক সারি এবং কলাম বলা হয়।
এই সংজ্ঞা অনুসারে, ম্যাট্রিক্স A-তে বেশ কয়েকটি ভিত্তি নাবালক থাকতে পারে।

পরিচয় ম্যাট্রিক্স E এর র্যাঙ্ক হল n (সারির সংখ্যা)।

উদাহরণ 1। দুটি ম্যাট্রিক্স দেওয়া, এবং তাদের নাবালক , . এদের মধ্যে কোনটিকে ভিত্তি হিসেবে নেওয়া যায়?
সমাধান. অপ্রধান M 1 =0, তাই এটি যেকোনও ম্যাট্রিক্সের ভিত্তি হতে পারে না। মাইনর M 2 =-9≠0 এবং এর ক্রম 2 আছে, তাই এটিকে A বা / এবং B এর ভিত্তি ম্যাট্রিক্স হিসাবে নেওয়া যেতে পারে, তবে শর্ত থাকে যে তাদের র্যাঙ্ক 2 এর সমান থাকে। যেহেতু detB=0 (দুটি আনুপাতিক কলাম সহ একটি নির্ধারক হিসাবে), তাহলে rangB=2 এবং M 2 ম্যাট্রিক্স B-এর ভিত্তি মাইনর হিসাবে নেওয়া যেতে পারে। ম্যাট্রিক্স A-এর র্যাঙ্ক 3, কারণ detA=-27≠ 0 এবং তাই, এই ম্যাট্রিক্সের বেসিস মাইনর অবশ্যই 3 হতে হবে, অর্থাৎ M 2 ম্যাট্রিক্স A-এর ভিত্তি নয়। উল্লেখ্য যে ম্যাট্রিক্স A-এর নির্ধারক A-এর সমান একটি অনন্য ভিত্তি গৌণ রয়েছে।

উপপাদ্য (মৌলিক অপ্রাপ্তবয়স্কের উপর)। একটি ম্যাট্রিক্সের যেকোনো সারি (কলাম) তার মৌলিক সারিগুলির (কলাম) একটি রৈখিক সমন্বয়।
উপপাদ্য থেকে ফলাফল.

র্যাঙ্ক r এর ম্যাট্রিক্সের যেকোনো (r+1) কলাম (সারি) রৈখিকভাবে নির্ভরশীল।
যদি একটি ম্যাট্রিক্সের র‍্যাঙ্ক তার সারি (কলাম) সংখ্যার চেয়ে কম হয়, তবে এর সারি (কলাম) রৈখিকভাবে নির্ভরশীল। যদি rangA এর সারি (কলাম) সংখ্যার সমান হয়, তাহলে সারি (কলাম) রৈখিকভাবে স্বাধীন।
একটি ম্যাট্রিক্স A এর নির্ধারক শূন্যের সমান যদি এবং শুধুমাত্র যদি এর সারি (কলাম) রৈখিকভাবে নির্ভরশীল হয়।
যদি ম্যাট্রিক্সের একটি সারিতে (কলাম) শূন্য ব্যতীত অন্য কোন সংখ্যা দ্বারা গুণিত অন্য সারি (কলাম) যোগ করা হয়, তাহলে ম্যাট্রিক্সের র‌্যাঙ্ক পরিবর্তন হবে না।
আপনি যদি ম্যাট্রিক্সে একটি সারি (কলাম) ক্রস আউট করেন, যা অন্যান্য সারি (কলাম) এর রৈখিক সমন্বয়, তাহলে ম্যাট্রিক্সের র‌্যাঙ্ক পরিবর্তন হবে না।
একটি ম্যাট্রিক্সের র‍্যাঙ্ক তার রৈখিকভাবে স্বাধীন সারিগুলির (কলাম) সর্বাধিক সংখ্যার সমান।
রৈখিকভাবে স্বাধীন সারির সর্বাধিক সংখ্যা রৈখিকভাবে স্বাধীন কলামের সর্বাধিক সংখ্যার সমান।

উদাহরণ 2। একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন .
সমাধান। একটি ম্যাট্রিক্সের র‍্যাঙ্কের সংজ্ঞার উপর ভিত্তি করে, আমরা শূন্য থেকে ভিন্ন সর্বোচ্চ ক্রমে একটি অপ্রাপ্তবয়স্কের সন্ধান করব। প্রথমত, আমরা ম্যাট্রিক্সকে একটি সহজ আকারে রূপান্তর করি। এটি করার জন্য, ম্যাট্রিক্সের প্রথম সারিটিকে (-2) দ্বারা গুণ করুন এবং দ্বিতীয়টিতে যোগ করুন, তারপরে এটিকে (-1) দ্বারা গুণ করুন এবং তৃতীয়টিতে যোগ করুন।

এবং বিষয়টির একটি গুরুত্বপূর্ণ ব্যবহারিক প্রয়োগ বিবেচনা করুন: সামঞ্জস্যের জন্য রৈখিক সমীকরণের একটি সিস্টেমের অধ্যয়ন.

একটি ম্যাট্রিক্স র্যাঙ্ক কি?

প্রবন্ধের হাস্যরসাত্মক এপিগ্রাফে প্রচুর পরিমাণে সত্য রয়েছে। "র্যাঙ্ক" শব্দটি সাধারণত কিছু ধরণের অনুক্রমের সাথে যুক্ত থাকে, বেশিরভাগ ক্ষেত্রেই ক্যারিয়ারের সিঁড়ির সাথে। একজন ব্যক্তির যত বেশি জ্ঞান, অভিজ্ঞতা, ক্ষমতা, সংযোগ ইত্যাদি থাকে। - তার অবস্থান এবং সুযোগের পরিধি তত বেশি। তারুণ্যের পরিভাষায়, র‌্যাঙ্ক বলতে বোঝায় সামগ্রিক মাত্রার "কঠিনতা"।

এবং আমাদের গাণিতিক ভাইয়েরা একই নীতিতে বাস করে। চলুন কিছু নির্বিচারে হাঁটার জন্য নিতে শূন্য ম্যাট্রিক্স:

ম্যাট্রিক্সে যদি চিন্তা করা যাক শুধুমাত্র শূন্য, তাহলে আমরা কোন পদে কথা বলতে পারি? সবাই অনানুষ্ঠানিক অভিব্যক্তি "মোট শূন্য" এর সাথে পরিচিত। ম্যাট্রিক্স সমাজে, সবকিছু ঠিক একই রকম:

জিরো ম্যাট্রিক্স র‌্যাঙ্কযে কোনো আকার শূন্য.

বিঃদ্রঃ : শূন্য ম্যাট্রিক্স গ্রীক অক্ষর "থেটা" দ্বারা চিহ্নিত করা হয়

ম্যাট্রিক্সের র‍্যাঙ্কটি আরও ভালভাবে বোঝার জন্য, এর পরে আমি উপকরণগুলি আঁকব বিশ্লেষণাত্মক জ্যামিতি. শূন্য বিবেচনা করুন ভেক্টরআমাদের ত্রিমাত্রিক স্থান, যা একটি নির্দিষ্ট দিক নির্ধারণ করে না এবং নির্মাণের জন্য অকেজো affine ভিত্তিতে. বীজগাণিতিক দৃষ্টিকোণ থেকে, একটি প্রদত্ত ভেক্টরের স্থানাঙ্কগুলি লেখা হয় ম্যাট্রিক্স"এক দ্বারা তিন" এবং যৌক্তিক (নির্দিষ্ট জ্যামিতিক অর্থে)অনুমান করুন যে এই ম্যাট্রিক্সের র্যাঙ্ক শূন্য।

এখন এর কয়েক তাকান অ-শূন্য কলাম ভেক্টরএবং সারি ভেক্টর:

প্রতিটি উদাহরণে অন্তত একটি অ-নাল উপাদান আছে, এবং এটি কিছু!

যেকোনো নন-জিরো সারি ভেক্টরের (কলাম ভেক্টর) র্যাঙ্ক একের সমান

এবং সাধারণভাবে বলতে গেলে - ম্যাট্রিক্সে থাকলে নির্বিচারে মাপঅন্তত একটি অ-শূন্য উপাদান আছে, তারপর তার র্যাঙ্ক কম নাইউনিট.

বীজগণিতীয় সারি এবং কলাম ভেক্টর একটি নির্দিষ্ট পরিমাণে বিমূর্ত, তাই আবার জ্যামিতিক সংযোগে ফিরে আসা যাক। অশূন্য ভেক্টরমহাকাশে একটি সু-সংজ্ঞায়িত দিক নির্ধারণ করে এবং এটি নির্মাণের জন্য উপযুক্ত ভিত্তি, তাই ম্যাট্রিক্সের র‌্যাঙ্ক একের সমান বলে ধরে নেওয়া হবে।

তত্ত্বীয় পেছনভাগ : রৈখিক বীজগণিতে, একটি ভেক্টর হল একটি ভেক্টর স্থানের একটি উপাদান (8টি স্বতঃসিদ্ধের মাধ্যমে সংজ্ঞায়িত), যা, বিশেষ করে, সংজ্ঞায়িত একটি বাস্তব সংখ্যা দ্বারা যোগ এবং গুণের ক্রিয়াকলাপ সহ বাস্তব সংখ্যাগুলির একটি ক্রমযুক্ত সারি (বা কলাম) হতে পারে তাদের জন্য. ভেক্টর সম্পর্কে আরও তথ্যের জন্য, নিবন্ধটি দেখুন রৈখিক রূপান্তর.

রৈখিকভাবে নির্ভরশীল(একে অপরের মাধ্যমে প্রকাশ করা হয়)। জ্যামিতিক দৃষ্টিকোণ থেকে, দ্বিতীয় লাইনে সমরেখা ভেক্টরের স্থানাঙ্ক রয়েছে , যা বিল্ডিং বিষয়টিকে অগ্রসর করেনি ত্রিমাত্রিক ভিত্তি, এই অর্থে অপ্রয়োজনীয় হচ্ছে. সুতরাং, এই ম্যাট্রিক্সের র্যাঙ্কও একের সমান।

আমরা কলামগুলিতে ভেক্টরগুলির স্থানাঙ্কগুলি পুনরায় লিখি ( ম্যাট্রিক্স স্থানান্তর):

পদমর্যাদায় কি পরিবর্তন হয়েছে? কিছুই না। কলামগুলি সমানুপাতিক, যার মানে হল একের সমান। যাইহোক, মনে রাখবেন যে তিনটি লাইনও সমানুপাতিক। তারা স্থানাঙ্ক সঙ্গে চিহ্নিত করা যেতে পারে তিনসমতলের সমরেখা ভেক্টর, যার মধ্যে শুধু একটাএকটি "ফ্ল্যাট" ভিত্তি নির্মাণের জন্য দরকারী। এবং এটি আমাদের র্যাঙ্কের জ্যামিতিক অনুভূতির সাথে সম্পূর্ণ একমত।

উপরের উদাহরণ থেকে একটি গুরুত্বপূর্ণ বিবৃতি অনুসরণ করে:

সারি দ্বারা একটি ম্যাট্রিক্সের র্যাঙ্ক কলাম দ্বারা একটি ম্যাট্রিক্সের র্যাঙ্কের সমান. আমি ইতিমধ্যে কার্যকরী পাঠে এটিকে কিছুটা উল্লেখ করেছি নির্ধারক গণনা করার পদ্ধতি.

বিঃদ্রঃ : সারিগুলির রৈখিক নির্ভরতা কলামগুলির রৈখিক নির্ভরতার দিকে নিয়ে যায় (এবং তদ্বিপরীত)। কিন্তু সময় বাঁচানোর জন্য, এবং অভ্যাসের বাইরে, আমি প্রায় সবসময় স্ট্রিংগুলির রৈখিক নির্ভরতা সম্পর্কে কথা বলব।

আসুন আমাদের প্রিয় পোষা প্রাণীকে প্রশিক্ষণ দেওয়া চালিয়ে যাই। তৃতীয় সারির ম্যাট্রিক্সে অন্য একটি সমরেখা ভেক্টরের স্থানাঙ্ক যোগ করুন :

তিনি কি ত্রিমাত্রিক ভিত্তি তৈরিতে আমাদের সাহায্য করেছিলেন? অবশ্যই না. তিনটি ভেক্টরই একই পথ ধরে সামনে পিছনে হেঁটে যায় এবং ম্যাট্রিক্সের র‍্যাঙ্ক অস্থির। আপনি যত খুশি সমরেখার ভেক্টর নিতে পারেন, 100 বলুন, তাদের স্থানাঙ্কগুলিকে 100 বাই 3 ম্যাট্রিক্সে রাখুন, এবং এই ধরনের একটি আকাশচুম্বী স্থান এখনও এক থাকবে।

আসুন ম্যাট্রিক্সের সাথে পরিচিত হই যার সারি রৈখিকভাবে স্বাধীন. ত্রিমাত্রিক ভিত্তি নির্মাণের জন্য একজোড়া নন-কোলিনিয়ার ভেক্টর উপযুক্ত। এই ম্যাট্রিক্সের র‌্যাঙ্ক হল দুই।

ম্যাট্রিক্সের র‌্যাঙ্ক কত? লাইনগুলি সমানুপাতিক বলে মনে হচ্ছে না ... তাই, তত্ত্বে, তিনটি। তবে এই ম্যাট্রিক্সের র‍্যাঙ্কও দুইটির সমান। আমি প্রথম দুটি লাইন যোগ করেছি এবং ফলাফলটি নীচে লিখেছি, অর্থাৎ রৈখিকভাবে প্রকাশিতপ্রথম দুই মাধ্যমে তৃতীয় লাইন. জ্যামিতিকভাবে, ম্যাট্রিক্সের সারি তিনটির স্থানাঙ্কের সাথে মিলে যায় কপ্ল্যানার ভেক্টর, এবং এই ট্রিপলের মধ্যে একজোড়া নন-কলিনিয়ার কমরেড রয়েছে।

আপনি দেখতে পারেন রৈখিক নির্ভরতাবিবেচিত ম্যাট্রিক্সে স্পষ্ট নয়, এবং আজ আমরা শিখব কীভাবে এটিকে "পরিষ্কার জলে" আনতে হয়।

আমি মনে করি অনেক মানুষ একটি ম্যাট্রিক্স র্যাঙ্ক কি অনুমান!

একটি ম্যাট্রিক্স যার সারি বিবেচনা করুন রৈখিকভাবে স্বাধীন. ভেক্টর গঠন affine ভিত্তিতে, এবং এই ম্যাট্রিক্সের র‌্যাঙ্ক হল তিনটি।

আপনি জানেন যে, ত্রিমাত্রিক স্থানের যেকোনো চতুর্থ, পঞ্চম, দশম ভেক্টর ভিত্তি ভেক্টরের পরিপ্রেক্ষিতে রৈখিকভাবে প্রকাশ করা হবে। অতএব, ম্যাট্রিক্সে যেকোন সংখ্যক সারি যোগ করা হলে তার ক্রম এখনও তিন হবে.

অনুরূপ যুক্তি বড় আকারের ম্যাট্রিক্সের জন্য বাহিত হতে পারে (স্পষ্টভাবে, ইতিমধ্যে জ্যামিতিক অর্থ ছাড়াই)।

সংজ্ঞা : ম্যাট্রিক্স র‌্যাঙ্ক হল রৈখিকভাবে স্বাধীন সারিগুলির সর্বাধিক সংখ্যা. বা: একটি ম্যাট্রিক্সের র‌্যাঙ্ক হল রৈখিকভাবে স্বাধীন কলামের সর্বোচ্চ সংখ্যা. হ্যাঁ, তারা সবসময় মেলে।

উপরোক্ত থেকে একটি গুরুত্বপূর্ণ ব্যবহারিক নির্দেশিকা অনুসরণ করা হয়েছে: একটি ম্যাট্রিক্সের র্যাঙ্ক তার ন্যূনতম মাত্রা অতিক্রম করে না. উদাহরণস্বরূপ, ম্যাট্রিক্সে চারটি সারি এবং পাঁচটি কলাম। ন্যূনতম মাত্রা চার, তাই এই ম্যাট্রিক্সের র‌্যাঙ্ক অবশ্যই 4-এর বেশি হবে না।

স্বরলিপি: বিশ্ব তত্ত্ব এবং অনুশীলনে ম্যাট্রিক্সের পদমর্যাদা নির্ধারণের জন্য কোনও সাধারণভাবে গৃহীত মান নেই, সবচেয়ে সাধারণটি পাওয়া যেতে পারে: - যেমন তারা বলে, একজন ইংরেজ এক জিনিস লেখেন, একজন জার্মান অন্য। অতএব, আমেরিকান এবং রাশিয়ান নরক সম্পর্কে সুপরিচিত উপাখ্যানের উপর ভিত্তি করে, আসুন একটি নেটিভ শব্দ দিয়ে ম্যাট্রিক্সের র‌্যাঙ্ক নির্ধারণ করি। উদাহরণ স্বরূপ: . এবং যদি ম্যাট্রিক্সটি "নামহীন" হয়, যার মধ্যে অনেকগুলি থাকে, তবে আপনি কেবল লিখতে পারেন।

অপ্রাপ্তবয়স্কদের ব্যবহার করে একটি ম্যাট্রিক্সের র‌্যাঙ্ক কীভাবে খুঁজে পাবেন?

যদি আমাদের ঠাকুরমার ম্যাট্রিক্সে একটি পঞ্চম কলাম থাকে, তবে আরও একটি 4 র্থ অর্ডার মাইনর ("নীল", "রাস্পবেরি" + 5 তম কলাম) গণনা করা উচিত ছিল।

উপসংহার: একটি অ-শূন্য নাবালকের সর্বোচ্চ ক্রম তিনটি, তাই।

সম্ভবত সবাই এই বাক্যাংশটি পুরোপুরি বুঝতে পারেনি: 4র্থ ক্রম অপ্রাপ্তবয়স্কটি শূন্যের সমান, তবে 3য় ক্রম অপ্রাপ্তবয়স্কদের মধ্যে একটি অ-শূন্য ছিল - তাই, সর্বাধিক আদেশ অ-শূন্যগৌণ এবং তিন সমান।

প্রশ্ন জাগে, অবিলম্বে নির্ধারক গণনা করা হচ্ছে না কেন? ঠিক আছে, প্রথমত, বেশিরভাগ কাজে ম্যাট্রিক্স বর্গাকার হয় না, এবং দ্বিতীয়ত, এমনকি যদি আপনি একটি অ-শূন্য মান পান, তবে টাস্কটি উচ্চ সম্ভাবনার সাথে প্রত্যাখ্যান করা হবে, কারণ এটি সাধারণত একটি স্ট্যান্ডার্ড বটম-আপ সমাধান বোঝায়। এবং বিবেচিত উদাহরণে, 4 র্থ ক্রমটির শূন্য নির্ণায়ক এমনকি আমাদের দাবি করতে দেয় যে ম্যাট্রিক্সের র‌্যাঙ্কটি চারের চেয়ে কম।

আমাকে অবশ্যই স্বীকার করতে হবে যে অপ্রাপ্তবয়স্কদের সীমান্তের পদ্ধতিটি আরও ভালভাবে ব্যাখ্যা করার জন্য আমি নিজেই বিশ্লেষণকৃত সমস্যাটি নিয়ে এসেছি। বাস্তব অনুশীলনে, সবকিছু সহজ:

উদাহরণ 2

অপ্রাপ্তবয়স্কদের ফ্রিং করার পদ্ধতি দ্বারা একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন

পাঠ শেষে সমাধান এবং উত্তর।

যখন অ্যালগরিদম দ্রুততম চলমান? আসুন একই চার-বাই-চার ম্যাট্রিক্সে ফিরে যাই . স্পষ্টতই, "ভাল" এর ক্ষেত্রে সমাধানটি সবচেয়ে সংক্ষিপ্ত হবে কোণার নাবালক:

এবং, যদি, তারপর, অন্যথায় - .

চিন্তাভাবনা মোটেও অনুমানমূলক নয় - এমন অনেক উদাহরণ রয়েছে যেখানে পুরো জিনিসটি কেবল কৌণিক নাবালকের মধ্যে সীমাবদ্ধ।

যাইহোক, কিছু ক্ষেত্রে, অন্য পদ্ধতি আরও কার্যকর এবং পছন্দনীয়:

কিভাবে গাউস পদ্ধতি ব্যবহার করে একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজে বের করবেন?

এই বিভাগটি পাঠকদের জন্য যারা ইতিমধ্যে পরিচিত গাউস পদ্ধতিএবং ধীরে ধীরে এটি তাদের হাত পেতে.

প্রযুক্তিগত দৃষ্টিকোণ থেকে, পদ্ধতিটি নতুন নয়:

1) প্রাথমিক রূপান্তর ব্যবহার করে, আমরা ম্যাট্রিক্সকে একটি ধাপে নিয়ে আসি;

2) ম্যাট্রিক্সের র্যাঙ্ক সারির সংখ্যার সমান।

এটা বেশ পরিষ্কার যে গাউস পদ্ধতি ব্যবহার করে ম্যাট্রিক্সের র‌্যাঙ্ক পরিবর্তন হয় না, এবং এখানে সারমর্মটি অত্যন্ত সহজ: অ্যালগরিদম অনুসারে, প্রাথমিক রূপান্তরগুলির সময়, সমস্ত অপ্রয়োজনীয় আনুপাতিক (রৈখিকভাবে নির্ভরশীল) লাইনগুলি সনাক্ত এবং সরানো হয়, যার ফলস্বরূপ একটি "শুকনো অবশিষ্টাংশ" অবশিষ্ট থাকে - সর্বাধিক সংখ্যা রৈখিকভাবে স্বাধীন লাইন।

আসুন পুরানো পরিচিত ম্যাট্রিক্সকে তিনটি সমরেখা ভেক্টরের স্থানাঙ্কের সাথে রূপান্তর করি:

(1) প্রথম সারিটি দ্বিতীয় সারিতে যোগ করা হয়েছে, -2 দ্বারা গুণ করা হয়েছে। প্রথম লাইনটি তৃতীয় লাইনে যোগ করা হয়েছে।

(2) জিরো লাইন মুছে ফেলা হয়।

তাই একটি লাইন বাকি আছে, তাই। বলা বাহুল্য, এটি 2য় ক্রমটির নয়টি শূন্য অপ্রাপ্তবয়স্ক গণনা করার চেয়ে অনেক দ্রুত এবং শুধুমাত্র তারপর একটি উপসংহার আঁকার।

আমি আপনাকে নিজেই মনে করিয়ে দিচ্ছি বীজগণিত ম্যাট্রিক্সকিছুই পরিবর্তন করা যাবে না, এবং রূপান্তরগুলি শুধুমাত্র পদ খুঁজে বের করার উদ্দেশ্যে সঞ্চালিত হয়! যাইহোক, আসুন আবার প্রশ্নটি নিয়ে আসি, কেন নয়? উৎস ম্যাট্রিক্স 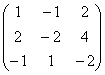ম্যাট্রিক্স এবং সারি তথ্য থেকে মৌলিকভাবে ভিন্ন তথ্য বহন করে। কিছু গাণিতিক মডেলে (অতিরিক্ততা ছাড়া), একটি সংখ্যার পার্থক্য জীবন এবং মৃত্যুর বিষয় হতে পারে। ... আমি প্রাথমিক এবং মাধ্যমিক গ্রেডের স্কুলের গণিত শিক্ষকদের মনে রেখেছিলাম, যারা অ্যালগরিদম থেকে সামান্যতম ভুল বা বিচ্যুতির জন্য নির্দয়ভাবে গ্রেডটি 1-2 পয়েন্ট দ্বারা কেটে দিয়েছিলেন। এবং এটি ভয়ানক হতাশাজনক ছিল যখন, আপাতদৃষ্টিতে গ্যারান্টিযুক্ত "পাঁচ" এর পরিবর্তে এটি "ভাল" বা আরও খারাপ পরিণত হয়েছিল। বোঝা অনেক পরে এসেছে - উপগ্রহ, পারমাণবিক ওয়ারহেড এবং পাওয়ার প্লান্টের সাথে একজন ব্যক্তিকে কীভাবে অর্পণ করা যায়? কিন্তু চিন্তা করবেন না, আমি এই এলাকায় কাজ করি না =)

আসুন আরও অর্থপূর্ণ কাজগুলিতে এগিয়ে যান, যেখানে অন্যান্য জিনিসগুলির মধ্যে, আমরা গুরুত্বপূর্ণ গণনামূলক কৌশলগুলির সাথে পরিচিত হব গাউস পদ্ধতি:

উদাহরণ 3

প্রাথমিক রূপান্তর ব্যবহার করে একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন

সমাধান: একটি চার-বাই-পাঁচ ম্যাট্রিক্স দেওয়া হয়েছে, যার অর্থ হল এটির র‍্যাঙ্ক অবশ্যই 4-এর বেশি নয়।

প্রথম কলামে, 1 বা -1 নেই, তাই কমপক্ষে একটি ইউনিট পেতে অতিরিক্ত পদক্ষেপের প্রয়োজন। সাইটের সমগ্র অস্তিত্ব জুড়ে, আমাকে বারবার প্রশ্ন করা হয়েছে: "প্রাথমিক রূপান্তরের সময় কলামগুলি পুনর্বিন্যাস করা কি সম্ভব?"। এখানে - প্রথম বা দ্বিতীয় কলাম পুনর্বিন্যাস, এবং সবকিছু ঠিক আছে! অধিকাংশ কাজে যেখানে গাউস পদ্ধতি, কলাম সত্যিই পুনর্বিন্যাস করা যেতে পারে. কিন্তু না. এবং বিন্দুটি ভেরিয়েবলের সাথে একটি সম্ভাব্য বিভ্রান্তিও নয়, বিন্দুটি হল উচ্চতর গণিত শেখানোর ক্লাসিক্যাল কোর্সে এই ক্রিয়াটি ঐতিহ্যগতভাবে বিবেচনা করা হয় না, তাই, এই জাতীয় কার্টিকে খুব বাঁকাভাবে দেখা হবে (বা এমনকি সবকিছু পুনরায় করতে বাধ্য করা হবে) .

দ্বিতীয় পয়েন্টটি সংখ্যা সম্পর্কিত। সিদ্ধান্ত নেওয়ার সময়, নিম্নলিখিত নিয়মগুলি দ্বারা পরিচালিত হওয়া দরকারী: প্রাথমিক রূপান্তর, যদি সম্ভব হয়, ম্যাট্রিক্সের সংখ্যা কমাতে হবে. সর্বোপরি, 23, 45 এবং 97 এর চেয়ে এক-দুই-তিনটির সাথে কাজ করা অনেক সহজ। এবং প্রথম ক্রিয়াটি শুধুমাত্র প্রথম কলামে একটি ইউনিট পাওয়ার লক্ষ্য নয়, বরং এটিকে নির্মূল করাও লক্ষ্য করে। সংখ্যা 7 এবং 11।

প্রথমে সম্পূর্ণ সমাধান, তারপর মন্তব্য:

(1) প্রথম সারিটি দ্বিতীয় সারিতে যোগ করা হয়েছে, -2 দ্বারা গুণ করা হয়েছে। প্রথম লাইনটি তৃতীয় লাইনে যোগ করা হয়েছে, -3 দ্বারা গুণ করা হয়েছে। এবং স্তূপে: 1ম লাইন, -1 দ্বারা গুণিত, 4র্থ লাইনে যোগ করা হয়েছে।

(2) শেষ তিনটি লাইন সমানুপাতিক। 3য় এবং 4র্থ লাইন মুছে ফেলা হয়েছে, দ্বিতীয় লাইন প্রথম স্থানে সরানো হয়েছে।

(3) প্রথম সারিটি দ্বিতীয় সারিতে যোগ করা হয়েছে, -3 দ্বারা গুণ করা হয়েছে।

একটি ধাপযুক্ত আকারে হ্রাস করা ম্যাট্রিক্সের দুটি সারি রয়েছে।

উত্তর:

এখন চার-বাই-চার ম্যাট্রিক্সে নির্যাতন করার পালা আপনার:

উদাহরণ 4

গাউসিয়ান পদ্ধতি ব্যবহার করে একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন

আমি আপনাকে মনে করিয়ে দিচ্ছি গাউস পদ্ধতিদ্ব্যর্থহীন অনমনীয়তা বোঝায় না এবং আপনার সমাধান সম্ভবত আমার সমাধান থেকে ভিন্ন হবে। পাঠের শেষে কাজের একটি সংক্ষিপ্ত নমুনা।

ম্যাট্রিক্সের র‌্যাঙ্ক বের করতে কোন পদ্ধতি ব্যবহার করবেন?

অনুশীলনে, এটি প্রায়শই বলা হয় না যে র্যাঙ্ক খুঁজে পেতে কোন পদ্ধতি ব্যবহার করা উচিত। এইরকম পরিস্থিতিতে, একজনকে শর্তটি বিশ্লেষণ করা উচিত - কিছু ম্যাট্রিক্সের জন্য এটি অপ্রাপ্তবয়স্কদের মাধ্যমে সমাধানটি পরিচালনা করা আরও যুক্তিযুক্ত, অন্যদের জন্য প্রাথমিক রূপান্তরগুলি প্রয়োগ করা অনেক বেশি লাভজনক:

উদাহরণ 5

একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন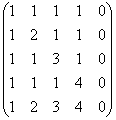

সমাধান: প্রথম উপায় একরকম অবিলম্বে অদৃশ্য হয়ে যায় =)

একটু উঁচুতে, আমি ম্যাট্রিক্সের কলামগুলিকে স্পর্শ না করার পরামর্শ দিয়েছিলাম, তবে যখন একটি শূন্য কলাম, বা সমানুপাতিক / মিলিত কলাম থাকে, তখনও এটি কেটে ফেলার উপযুক্ত:

(1) পঞ্চম কলামটি শূন্য, আমরা এটিকে ম্যাট্রিক্স থেকে সরিয়ে ফেলি। এইভাবে, ম্যাট্রিক্সের র‌্যাঙ্ক সর্বোচ্চ চারটি। প্রথম সারিটি -1 দ্বারা গুণ করা হয়। এটি গাউসিয়ান পদ্ধতির আরেকটি স্বাক্ষর বৈশিষ্ট্য, যা নিম্নলিখিত ক্রিয়াটিকে একটি আনন্দদায়ক হাঁটা করে তোলে:

(2) সমস্ত লাইনে, দ্বিতীয় দিয়ে শুরু করে, প্রথম লাইন যোগ করা হয়েছে।

(3) প্রথম সারিটি -1 দ্বারা গুন করা হয়েছিল, তৃতীয় সারিটিকে 2 দ্বারা ভাগ করা হয়েছিল, চতুর্থ সারিটিকে 3 দ্বারা ভাগ করা হয়েছিল৷ দ্বিতীয় সারিটিকে -1 দ্বারা গুণ করা হয়েছিল পঞ্চম সারিতে যোগ করা হয়েছিল৷

(4) তৃতীয় লাইনটি পঞ্চম লাইনে যোগ করা হয়েছে, -2 দ্বারা গুণ করা হয়েছে।

(5) শেষ দুটি লাইন সমানুপাতিক, আমরা পঞ্চমটি মুছে ফেলি।

ফলাফল হল 4 সারি।

উত্তর:

স্ব-অন্বেষণের জন্য স্ট্যান্ডার্ড পাঁচ-তলা বিল্ডিং:

উদাহরণ 6

একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন

পাঠ শেষে সংক্ষিপ্ত সমাধান এবং উত্তর।

এটি লক্ষ করা উচিত যে "ম্যাট্রিক্স র্যাঙ্ক" শব্দটি অনুশীলনে এত সাধারণ নয় এবং বেশিরভাগ সমস্যায় আপনি এটি ছাড়া করতে পারেন। তবে একটি কাজ রয়েছে যেখানে বিবেচনাধীন ধারণাটি প্রধান চরিত্র, এবং নিবন্ধের উপসংহারে আমরা এই ব্যবহারিক প্রয়োগটি বিবেচনা করব:

সামঞ্জস্যের জন্য রৈখিক সমীকরণের সিস্টেমটি কীভাবে তদন্ত করবেন?

প্রায়শই, সমাধান ছাড়াও রৈখিক সমীকরণের সিস্টেমশর্ত অনুসারে, প্রথমে এটিকে সামঞ্জস্যের জন্য পরীক্ষা করতে হবে, অর্থাৎ প্রমাণ করতে হবে যে কোনও সমাধান আদৌ বিদ্যমান। এই যাচাইকরণে একটি মূল ভূমিকা পালন করা হয় ক্রোনেকার-ক্যাপেলি উপপাদ্য, যা আমি প্রয়োজনীয় আকারে প্রণয়ন করব:

র‍্যাঙ্ক হলে সিস্টেম ম্যাট্রিক্সপদমর্যাদার সমান বর্ধিত ম্যাট্রিক্স সিস্টেম, তাহলে সিস্টেমটি সামঞ্জস্যপূর্ণ, এবং যদি প্রদত্ত সংখ্যাটি অজানা সংখ্যার সাথে মিলে যায়, তাহলে সমাধানটি অনন্য।

সুতরাং, সামঞ্জস্যের জন্য সিস্টেম অধ্যয়ন করার জন্য, সমতা পরীক্ষা করা প্রয়োজন , কোথায় - সিস্টেম ম্যাট্রিক্স(পাঠ থেকে পরিভাষা মনে রাখবেন গাউস পদ্ধতি), ক - বর্ধিত ম্যাট্রিক্স সিস্টেম(যেমন ভেরিয়েবলে সহগ সহ ম্যাট্রিক্স + মুক্ত পদের কলাম)।

এই নিবন্ধটি ম্যাট্রিক্সের র্যাঙ্ক এবং প্রয়োজনীয় অতিরিক্ত ধারণাগুলির মতো একটি ধারণা নিয়ে আলোচনা করবে। আমরা একটি ম্যাট্রিক্সের র‌্যাঙ্ক খুঁজে বের করার উদাহরণ এবং প্রমাণ দেব এবং আপনাকেও বলব যে ম্যাট্রিক্স মাইনর কী এবং কেন এটি এত গুরুত্বপূর্ণ।

Yandex.RTB R-A-339285-1

ম্যাট্রিক্স মাইনর

ম্যাট্রিক্সের র্যাঙ্ক কী তা বোঝার জন্য, ম্যাট্রিক্স মাইনর হিসাবে এই জাতীয় ধারণাটি বোঝা প্রয়োজন।

সংজ্ঞা 1

গৌণkতম ক্রম ম্যাট্রিক্স - k × k ক্রমের একটি বর্গ ম্যাট্রিক্সের নির্ধারক, যা ম্যাট্রিক্স A-এর উপাদানগুলির সমন্বয়ে গঠিত, ম্যাট্রিক্স A-এর উপাদানগুলির অবস্থান বজায় রেখে পূর্ব-নির্বাচিত k-সারি এবং k-কলামগুলিতে অবস্থিত।

সহজ কথায়, যদি আমরা ম্যাট্রিক্স A-তে (p-k) সারি এবং (n-k) কলামগুলি মুছে ফেলি এবং ম্যাট্রিক্স A-এর উপাদানগুলির বিন্যাস বজায় রেখে অবশিষ্ট উপাদানগুলির একটি ম্যাট্রিক্স তৈরি করি, তাহলে ফলাফল ম্যাট্রিক্সের নির্ধারক হবে ম্যাট্রিক্স A-এর ক্রম k-এর নাবালক।

এটি উদাহরণ থেকে অনুসরণ করে যে ম্যাট্রিক্স A-এর প্রথম-ক্রম অপ্রাপ্তবয়স্করা ম্যাট্রিক্স উপাদানগুলি নিজেই।

আমরা ২য় ক্রমে অপ্রাপ্তবয়স্কদের বেশ কয়েকটি উদাহরণ দিতে পারি। দুটি সারি এবং দুটি কলাম বেছে নেওয়া যাক। উদাহরণস্বরূপ, ১ম ও ২য় সারি, ৩য় ও ৪র্থ কলাম।

উপাদানগুলির এই পছন্দের সাথে, দ্বিতীয় ক্রমটির অপ্রধান হবে - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

ম্যাট্রিক্স A-এর আরেকটি 2য় ক্রম মাইনর হল 0 0 1 1 = 0

ম্যাট্রিক্স A-এর দ্বিতীয়-ক্রম নাবালকদের নির্মাণের উদাহরণ দেওয়া যাক:

ম্যাট্রিক্স A-এর তৃতীয় কলামটি মুছে দিয়ে 3য় অর্ডার মাইনর পাওয়া যায়:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

ম্যাট্রিক্স A-এর 3য় অর্ডার মাইনর কীভাবে পাওয়া যায় তার একটি চিত্র:

একটি প্রদত্ত ম্যাট্রিক্সের জন্য, 3য় ক্রম থেকে উচ্চতর কোন অপ্রাপ্তবয়স্ক নেই, কারণ

k ≤ m i n (p , n) = m i n (3 , 4) = 3

pxn অর্ডারের একটি ম্যাট্রিক্স A-এর জন্য কত k-th ক্রম নাবালক আছে?

অপ্রাপ্তবয়স্কদের সংখ্যা নিম্নলিখিত সূত্র ব্যবহার করে গণনা করা হয়:

C p k × C n k , g e C p k = p ! k! (p - k)! এবং C nk = n! k! (n - k)! - যথাক্রমে p থেকে k, n থেকে k পর্যন্ত সংমিশ্রণের সংখ্যা।

ম্যাট্রিক্স A-এর অপ্রাপ্তবয়স্করা কী তা আমরা সিদ্ধান্ত নেওয়ার পরে, আমরা ম্যাট্রিক্স A-এর র্যাঙ্ক নির্ধারণে এগিয়ে যেতে পারি।

ম্যাট্রিক্স র‌্যাঙ্ক: খোঁজার পদ্ধতি

সংজ্ঞা 2

ম্যাট্রিক্স র‌্যাঙ্ক - শূন্য ছাড়া ম্যাট্রিক্সের সর্বোচ্চ ক্রম।

পদবী ১

পদমর্যাদা (A), Rg(A), Rang(A)।

একটি ম্যাট্রিক্সের র্যাঙ্ক এবং একটি ম্যাট্রিক্সের মাইনর এর সংজ্ঞা থেকে, এটি পরিষ্কার হয়ে যায় যে একটি শূন্য ম্যাট্রিক্সের র্যাঙ্ক শূন্যের সমান এবং একটি নন-জিরো ম্যাট্রিক্সের র্যাঙ্ক শূন্য থেকে আলাদা।

সংজ্ঞা অনুসারে ম্যাট্রিক্সের র‌্যাঙ্ক খোঁজা

সংজ্ঞা 3

ক্ষুদ্র গণনা পদ্ধতি - একটি ম্যাট্রিক্সের র্যাঙ্ক নির্ধারণের উপর ভিত্তি করে একটি পদ্ধতি।

অপ্রাপ্তবয়স্কদের গণনা দ্বারা কর্মের অ্যালগরিদম :

অর্ডারের ম্যাট্রিক্স A এর র্যাঙ্ক খুঁজে বের করা প্রয়োজন পি× n. যদি কমপক্ষে একটি অ-শূন্য উপাদান থাকে, তবে ম্যাট্রিক্সের র্যাঙ্কটি কমপক্ষে একটি ( কারণ একটি 1ম ক্রম ছোট যা শূন্যের সমান নয়৷).

তারপর 2য় ক্রম অপ্রাপ্তবয়স্কদের গণনা অনুসরণ করে. যদি সমস্ত 2য় ক্রম অপ্রাপ্তবয়স্ক শূন্যের সমান হয়, তাহলে র্যাঙ্কটি একের সমান। যদি 2য় ক্রমটির কমপক্ষে একটি অ-শূন্য নাবালক থাকে, তবে 3য় ক্রমটির অপ্রাপ্তবয়স্কদের গণনায় যেতে হবে এবং এই ক্ষেত্রে ম্যাট্রিক্সের র্যাঙ্কটি কমপক্ষে দুটির সমান হবে৷

আসুন 3য় ক্রমটির র্যাঙ্কের সাথে একই কাজ করি: যদি ম্যাট্রিক্সের সমস্ত অপ্রাপ্তবয়স্ক শূন্যের সমান হয়, তাহলে র্যাঙ্কটি দুইটির সমান হবে। যদি কমপক্ষে একটি নন-জিরো থার্ড-অর্ডার মাইনর থাকে, তাহলে ম্যাট্রিক্সের র‌্যাঙ্ক কমপক্ষে তিনটি। এবং তাই, উপমা দ্বারা.

উদাহরণ 2

একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন:

A \u003d - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

যেহেতু ম্যাট্রিক্স অ-শূন্য, তাই এর র‌্যাঙ্ক অন্তত একের সমান।

২য় ক্রম অপ্রধান - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 অ-শূন্য। এটি বোঝায় যে ম্যাট্রিক্স A-এর র্যাঙ্ক কমপক্ষে দুটি।

আমরা 3য় অর্ডারের অপ্রাপ্তবয়স্কদের মাধ্যমে সাজাই: C 3 3 × C 5 3 \u003d 1 5 ! 3! (5 - 3)! = 10 টুকরা।

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0

1 1 - 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

3য় ক্রম অপ্রাপ্তবয়স্ক শূন্য, তাই ম্যাট্রিক্সের র‌্যাঙ্ক হল দুই।

উত্তর : র‍্যাঙ্ক (A) = 2।

অপ্রাপ্তবয়স্কদের ফ্রিং করার পদ্ধতি দ্বারা একটি ম্যাট্রিক্সের র‌্যাঙ্ক খোঁজা

সংজ্ঞা 3

ফ্রিংিং মাইনর পদ্ধতি - একটি পদ্ধতি যা আপনাকে কম গণনামূলক কাজের সাথে ফলাফল পেতে দেয়।

ছোট ছোট fringing - অপ্রাপ্তবয়স্ক M o k (k + 1)- ম্যাট্রিক্স A-এর তম ক্রম, যা ম্যাট্রিক্স A-এর ক্রম k-এর গৌণ M-এর সীমানা, যদি নাবালক M o k-এর সাথে মিলিত ম্যাট্রিক্সে "ধারণ" থাকে যা নাবালকের সাথে মিলে যায় এম.

সহজ কথায়, একটি সারি এবং একটি কলামের উপাদানগুলি মুছে ফেলার মাধ্যমে সীমানাযুক্ত মাইনর M-এর সাথে সম্পর্কিত ম্যাট্রিক্সটি বর্ডারিং মাইনর M o k-এর সাথে সম্পর্কিত ম্যাট্রিক্স থেকে পাওয়া যায়।

উদাহরণ 3

একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজুন:

A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

র‍্যাঙ্ক খুঁজে বের করতে, আমরা ২য় ক্রম ছোট M = 2 - 1 4 1 নিই

আমরা সমস্ত সীমান্তবর্তী নাবালকদের লিখি:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

অপ্রাপ্তবয়স্কদের সীমানা নির্ধারণের পদ্ধতিকে প্রমাণ করার জন্য, আমরা একটি উপপাদ্য উপস্থাপন করি যার প্রণয়নের জন্য প্রমাণ ভিত্তির প্রয়োজন নেই।

উপপাদ্য ঘ

যদি একটি ম্যাট্রিক্স A-এর k-th ক্রম অপ্রাপ্তবয়স্কদের সীমানাভুক্ত সমস্ত অপ্রাপ্তবয়স্করা n দ্বারা ক্রম শূন্যের সমান হয়, তাহলে ম্যাট্রিক্স A-এর সমস্ত অপ্রাপ্তবয়স্ক ক্রম (k + 1) শূন্যের সমান।

অ্যাকশন অ্যালগরিদম :

একটি ম্যাট্রিক্সের র্যাঙ্ক খুঁজে পেতে, সমস্ত অপ্রাপ্তবয়স্কদের মধ্য দিয়ে যেতে হবে না, শুধু সীমানাগুলি দেখুন।

যদি সীমান্তবর্তী অপ্রাপ্তবয়স্করা শূন্যের সমান হয়, তাহলে ম্যাট্রিক্সের র‌্যাঙ্ক শূন্য। যদি কমপক্ষে একটি নাবালক থাকে যা শূন্যের সমান নয়, তাহলে আমরা সীমানাযুক্ত নাবালকদের বিবেচনা করি।

যদি তারা সব শূন্য হয়, তাহলে র‍্যাঙ্ক(A) হল দুটি। যদি অন্তত একটি অশূন্য সীমানা নাবালক থাকে, তাহলে আমরা এর সীমানা নাবালক বিবেচনা করতে এগিয়ে যাই। এবং তাই, একটি অনুরূপ ভাবে.

উদাহরণ 4

A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

কিভাবে সিদ্ধান্ত নিতে?

যেহেতু ম্যাট্রিক্স A-এর 11 উপাদানটি শূন্যের সমান নয়, তাই আমরা 1ম ক্রমটির অপ্রাপ্তবয়স্ক নিই। শূন্য ব্যতীত অন্য একটি বর্ডারিং মাইনর খোঁজা শুরু করা যাক:

2 1 4 2 = 2 x 2 - 1 x 4 = 0 2 0 4 1 = 2 x 1 - 0 x 4 = 2

আমরা 2য় ক্রমটির একটি বর্ডারিং মাইনর পেয়েছি যা শূন্য 2 0 4 1 এর সমান নয়।

বর্ডারিং নাবালকদের গণনা করা যাক - (এখানে (4 - 2) × (5 - 2) = 6 টুকরা আছে)।

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

উত্তর : র‍্যাঙ্ক(A) = 2।

গাউস পদ্ধতি দ্বারা একটি ম্যাট্রিক্সের র্যাঙ্ক খোঁজা (প্রাথমিক রূপান্তর ব্যবহার করে)

প্রাথমিক রূপান্তরগুলি কী তা স্মরণ করুন।

প্রাথমিক রূপান্তর:

ম্যাট্রিক্সের সারি (কলাম) পুনর্বিন্যাস করে;
ম্যাট্রিক্সের যেকোনো সারির (কলাম) সমস্ত উপাদানকে একটি নির্বিচারে অ-শূন্য সংখ্যা k দ্বারা গুণ করে;

ম্যাট্রিক্সের অন্য সারি (কলাম) এর সাথে সামঞ্জস্যপূর্ণ যেকোন সারি (কলাম) উপাদানগুলির উপাদানগুলির সাথে যোগ করে, যা একটি নির্বিচারে সংখ্যা k দ্বারা গুণিত হয়৷

সংজ্ঞা 5

গাউস পদ্ধতি ব্যবহার করে ম্যাট্রিক্সের র‌্যাঙ্ক খোঁজা - ম্যাট্রিক্স সমতুলতার তত্ত্বের উপর ভিত্তি করে একটি পদ্ধতি: যদি একটি সীমিত সংখ্যক প্রাথমিক রূপান্তর ব্যবহার করে ম্যাট্রিক্স A থেকে ম্যাট্রিক্স B পাওয়া যায়, তাহলে Rank(A) = Rank(B)।

এই বিবৃতিটির বৈধতা ম্যাট্রিক্সের সংজ্ঞা থেকে অনুসরণ করে:

একটি ম্যাট্রিক্সের সারি বা কলামের স্থানান্তরের ক্ষেত্রে, এর নির্ধারক পরিবর্তন চিহ্ন। যদি এটি শূন্যের সমান হয়, তবে সারি বা কলামগুলিকে অনুমতি দেওয়ার সময় এটি শূন্যের সমান থাকে;
ম্যাট্রিক্সের যেকোনো সারির (কলাম) সমস্ত উপাদানকে একটি নির্বিচারে সংখ্যা k দ্বারা গুণ করার ক্ষেত্রে, যা শূন্যের সমান নয়, ফলাফল ম্যাট্রিক্সের নির্ধারক মূল ম্যাট্রিক্সের নির্ধারকের সমান, যা গুণিত হয় k দ্বারা;

ম্যাট্রিক্সের একটি নির্দিষ্ট সারি বা কলামের উপাদানগুলির সাথে যোগ করার ক্ষেত্রে অন্য সারি বা কলামের সংশ্লিষ্ট উপাদানগুলি, যা k সংখ্যা দ্বারা গুণিত হয়, তার নির্ধারক পরিবর্তন করে না।

প্রাথমিক রূপান্তর পদ্ধতির সারমর্ম : প্রাথমিক রূপান্তর ব্যবহার করে ম্যাট্রিক্সকে কম করুন, যার র‍্যাঙ্ক খুঁজে পাওয়া যাবে।

কি জন্য?

এই ধরনের ম্যাট্রিক্সের র‌্যাঙ্ক খুঁজে পাওয়া বেশ সহজ। এটি অন্তত একটি নন-নাল উপাদান আছে এমন সারির সংখ্যার সমান। এবং যেহেতু প্রাথমিক রূপান্তরের সময় র‌্যাঙ্ক পরিবর্তন হয় না, তাই এটি হবে ম্যাট্রিক্সের র‌্যাঙ্ক।

আসুন এই প্রক্রিয়াটি ব্যাখ্যা করি:

আয়তক্ষেত্রাকার ম্যাট্রিক্সের জন্য A এর ক্রম p দ্বারা n, যার সারির সংখ্যা কলামের সংখ্যার চেয়ে বেশি:

A ~ 1 খ 12 খ 13 ⋯ b 1 n - 1 খ 1 n 0 1 খ 23 ⋯ b 2 n - 2 খ 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 খ n - 1 0 0 01 0 0 0 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 0 0 , R a n k (A) = n

ক ~ 1 খ 12 খ 13 √ খ 1 কে খ 1 কে + 1 খ 1 এন 0 1 খ 23 ⋯ খ 2 কে খ 2 কে + 1 ⋯ বি 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 k + 0 k + 10 1 ⋯ b k n 0 0 0 0 0 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 0 0 0 , R a n k (A) = k

আয়তক্ষেত্রাকার ম্যাট্রিক্সের জন্য A এর ক্রম p দ্বারা n, যার সারির সংখ্যা কলামের সংখ্যার চেয়ে কম:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 p + 100 1 ⋯ b p n , R a n k (A) = p

ক ~ 1 খ 12 খ 13 √ খ 1 কে খ 1 কে + 1 খ 1 এন 0 1 খ 23 ⋯ খ 2 কে খ 2 কে + 1 ⋯ বি 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 k + 0 k + 10 1 ⋯ b k n 0 0 0 0 0 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 0 0 0 0

বর্গাকার ম্যাট্রিক্সের জন্য A এর ক্রম n দ্বারা n:

A ~ 1 খ 12 খ 13 ⋯ b 1 n - 1 খ 1 n 0 1 খ 23 ⋯ খ 2 n - 1 খ 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 খ n - 1 0 0 01 , R a n k (A) = n

ক ~ 1 খ 12 খ 13 √ খ 1 কে খ 1 কে + 1 খ 1 এন 0 1 খ 23 ⋯ খ 2 কে খ 2 কে + 1 ⋯ বি 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 k + 0 k + 10 1 ⋯ b k n 0 0 0 0 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 0 0 0 , R a n k (A) = k, k< n

উদাহরণ 5

প্রাথমিক রূপান্তর ব্যবহার করে ম্যাট্রিক্স A এর র্যাঙ্ক খুঁজুন:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

কিভাবে সিদ্ধান্ত নিতে?

যেহেতু একটি 11 উপাদানটি অ-শূন্য, তাই ম্যাট্রিক্স A এর প্রথম সারির উপাদানগুলিকে 1 a 11 \u003d 1 2 দ্বারা গুণ করতে হবে:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

আমরা ২য় সারির উপাদানে ১ম সারির সংশ্লিষ্ট উপাদান যোগ করি, যেগুলোকে (-৩) দ্বারা গুণ করা হয়। 3য় সারির উপাদানগুলিতে আমরা 1ম সারির উপাদানগুলি যোগ করি, যা (-1) দ্বারা গুণিত হয়:

~ A (1) \u003d 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) \u003d \u003d 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) ) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

একটি 22 (2) উপাদানটি অ-শূন্য, তাই আমরা ম্যাট্রিক্স A এর 2য় সারির উপাদানগুলিকে A (2) দ্বারা 1 a 22 (2) = - 2 3 দ্বারা গুণ করি:

A (3) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0

ফলস্বরূপ ম্যাট্রিক্সের 3য় সারির উপাদানগুলিতে, আমরা 2য় সারির সংশ্লিষ্ট উপাদানগুলি যোগ করি, যা 3 2 দ্বারা গুণিত হয়;
4র্থ সারির উপাদানগুলিতে - 2য় সারির উপাদানগুলি, যা 9 2 দ্বারা গুণিত হয়;
5 তম সারির উপাদানগুলিতে - 2য় সারির উপাদানগুলি, যা 3 2 দ্বারা গুণ করা হয়।

সমস্ত সারি উপাদান শূন্য. এইভাবে, প্রাথমিক রূপান্তরের সাহায্যে, আমরা ম্যাট্রিক্সকে একটি ট্র্যাপিজয়েডাল আকারে হ্রাস করেছি, যেখান থেকে দেখা যায় যে R a n k (A (4)) = 2। এটি অনুসরণ করে যে মূল ম্যাট্রিক্সের র্যাঙ্কও দুইটির সমান।

মন্তব্য করুন

আপনি যদি প্রাথমিক রূপান্তরগুলি সম্পাদন করেন, তাহলে আনুমানিক মান অনুমোদিত নয়!

আপনি যদি পাঠ্যটিতে একটি ভুল লক্ষ্য করেন, অনুগ্রহ করে এটি হাইলাইট করুন এবং Ctrl+Enter টিপুন

কিছু ম্যাট্রিক্স দেওয়া যাক:

এই ম্যাট্রিক্সে নির্বাচন করুন নির্বিচারে লাইন এবং নির্বিচারে কলাম
. তারপর নির্ধারক তম ক্রম, ম্যাট্রিক্স উপাদানের সমন্বয়ে গঠিত
নির্বাচিত সারি এবং কলামের সংযোগস্থলে অবস্থিত একটি মাইনর বলা হয় -ম ক্রম ম্যাট্রিক্স
.

সংজ্ঞা 1.13।ম্যাট্রিক্স র‌্যাঙ্ক
এই ম্যাট্রিক্সের অ-শূন্য মাইনর এর বৃহত্তম ক্রম।

একটি ম্যাট্রিক্সের র্যাঙ্ক গণনা করার জন্য, একজনকে তার সব ছোট ক্রম বিবেচনা করা উচিত এবং, যদি তাদের মধ্যে অন্তত একটি অশূন্য হয়, তাহলে সর্বোচ্চ ক্রমে অপ্রাপ্তবয়স্কদের বিবেচনায় এগিয়ে যান। ম্যাট্রিক্সের র‌্যাঙ্ক নির্ধারণের এই পদ্ধতিটিকে বর্ডারিং পদ্ধতি (বা বর্ডারিং নাবালক পদ্ধতি) বলা হয়।

টাস্ক 1.4।অপ্রাপ্তবয়স্কদের সীমান্তের পদ্ধতি দ্বারা, একটি ম্যাট্রিক্সের র্যাঙ্ক নির্ধারণ করুন
.

প্রথম-ক্রম বর্ডারিং বিবেচনা করুন, উদাহরণস্বরূপ,
. তারপর আমরা দ্বিতীয় ক্রম কিছু সীমানা বিবেচনা চালু.

উদাহরণ স্বরূপ,
.

পরিশেষে, আসুন তৃতীয় আদেশের সীমানা বিশ্লেষণ করি।

সুতরাং একটি অ-শূন্য মাইনর এর সর্বোচ্চ ক্রম হল 2, তাই
.

সমস্যা 1.4 সমাধান করার সময়, কেউ লক্ষ্য করতে পারে যে দ্বিতীয় ক্রমের সীমানা নাবালকের সিরিজ অশূন্য। এই বিষয়ে, নিম্নলিখিত ধারণা সঞ্চালিত হয়.

সংজ্ঞা 1.14।একটি ম্যাট্রিক্সের বেসিস মাইনর হল যেকোন নন-জিরো মাইনর যার ক্রম ম্যাট্রিক্সের র্যাঙ্কের সমান।

উপপাদ্য 1.2।(মৌলিক গৌণ উপপাদ্য)। মৌলিক সারি (বেসিক কলাম) রৈখিকভাবে স্বাধীন।

মনে রাখবেন যে একটি ম্যাট্রিক্সের সারি (কলাম) রৈখিকভাবে নির্ভরশীল যদি এবং শুধুমাত্র যদি তাদের মধ্যে অন্তত একটিকে অন্যদের একটি রৈখিক সমন্বয় হিসাবে উপস্থাপন করা যায়।

উপপাদ্য 1.3।রৈখিকভাবে স্বাধীন ম্যাট্রিক্স সারির সংখ্যা রৈখিকভাবে স্বাধীন ম্যাট্রিক্স কলামের সংখ্যার সমান এবং ম্যাট্রিক্সের র্যাঙ্কের সমান।

উপপাদ্য 1.4।(নির্ধারক শূন্যের সমান হওয়ার জন্য প্রয়োজনীয় এবং পর্যাপ্ত শর্ত)। নির্ধারক জন্য -ম আদেশ শূন্যের সমান, এটি প্রয়োজনীয় এবং যথেষ্ট যে এর সারি (কলাম) রৈখিকভাবে নির্ভরশীল।

এর সংজ্ঞার উপর ভিত্তি করে একটি ম্যাট্রিক্সের র্যাঙ্ক গণনা করা খুবই কষ্টকর। এটি হাই-অর্ডার ম্যাট্রিক্সের জন্য বিশেষভাবে গুরুত্বপূর্ণ হয়ে ওঠে। এই বিষয়ে, অনুশীলনে, একটি ম্যাট্রিক্সের র্যাঙ্ক গণনা করা হয় উপপাদ্য 10.2 - 10.4 প্রয়োগের উপর ভিত্তি করে, সেইসাথে ম্যাট্রিক্স সমতুল্যতা এবং প্রাথমিক রূপান্তরের ধারণাগুলির ব্যবহারের উপর ভিত্তি করে।

সংজ্ঞা 1.15।দুটি ম্যাট্রিক্স
এবং সমতুল্য বলা হয় যদি তাদের পদমর্যাদা সমান হয়, যেমন
.

ম্যাট্রিস হলে
এবং সমতুল্য, তারপর নোট করুন
 .

উপপাদ্য 1.5।একটি ম্যাট্রিক্সের র্যাঙ্ক প্রাথমিক রূপান্তর থেকে পরিবর্তিত হয় না।

আমরা ম্যাট্রিক্সের প্রাথমিক রূপান্তর বলব
ম্যাট্রিক্সে নিম্নলিখিত ক্রিয়াগুলির যে কোনও একটি:

সারিগুলিকে কলাম এবং কলামগুলি সংশ্লিষ্ট সারিগুলির সাথে প্রতিস্থাপন করা;

ম্যাট্রিক্স সারির স্থানান্তর;

একটি রেখা অতিক্রম করা, যার সমস্ত উপাদান শূন্যের সমান;

কোনো স্ট্রিংকে অ-শূন্য সংখ্যা দ্বারা গুণ করা;

এক সারির উপাদানে যোগ করলে অন্য সারির সংশ্লিষ্ট উপাদান একই সংখ্যা দ্বারা গুণিত হয়
.

উপপাদ্যের ফলাফল 1.5।ম্যাট্রিক্স হলে
ম্যাট্রিক্স থেকে প্রাপ্ত একটি সীমিত সংখ্যক প্রাথমিক রূপান্তর ব্যবহার করে, তারপর ম্যাট্রিক্স
এবং সমতুল্য

একটি ম্যাট্রিক্সের র্যাঙ্ক গণনা করার সময়, প্রাথমিক রূপান্তরগুলির একটি সীমিত সংখ্যক ব্যবহার করে এটি একটি ট্র্যাপিজয়েডাল আকারে হ্রাস করা উচিত।

সংজ্ঞা 1.16।আমরা ট্র্যাপিজয়েডালকে একটি ম্যাট্রিক্সের প্রতিনিধিত্বের এমন একটি রূপ বলব যখন শূন্য ছাড়া অন্য বৃহত্তম ক্রমটির সীমানাযুক্ত ক্ষুদ্র অংশে, তির্যকগুলির নীচের সমস্ত উপাদান অদৃশ্য হয়ে যায়। উদাহরণ স্বরূপ:

এখানে
, ম্যাট্রিক্স উপাদান
শূন্যে পরিণত তাহলে এই ধরনের ম্যাট্রিক্সের প্রতিনিধিত্বের ফর্ম ট্র্যাপিজয়েডাল হবে।

একটি নিয়ম হিসাবে, গাউসিয়ান অ্যালগরিদম ব্যবহার করে ম্যাট্রিক্সগুলিকে ট্র্যাপিজয়েডাল আকারে হ্রাস করা হয়। গাউসিয়ান অ্যালগরিদমের ধারণাটি হল, ম্যাট্রিক্সের প্রথম সারির উপাদানগুলিকে সংশ্লিষ্ট কারণগুলির দ্বারা গুণ করে, তারা অর্জন করে যে উপাদানটির নীচে অবস্থিত প্রথম কলামের সমস্ত উপাদান
, শূন্যে পরিণত হবে। তারপরে, সংশ্লিষ্ট গুণক দ্বারা দ্বিতীয় কলামের উপাদানগুলিকে গুণ করে, আমরা অর্জন করতে পারি যে উপাদানটির নীচে অবস্থিত দ্বিতীয় কলামের সমস্ত উপাদান
, শূন্যে পরিণত হবে। আরও একইভাবে এগিয়ে যান.