কিভাবে একটি ম্যাট্রিক্স চেক. বিপরীত ম্যাট্রিক্স এবং এর বৈশিষ্ট্য। অজানাদের গাউসিয়ান নির্মূল দ্বারা বিপরীত ম্যাট্রিক্স সন্ধান করা

ম্যাট্রিক্স বীজগণিত - বিপরীত ম্যাট্রিক্স

বিপরীত ম্যাট্রিক্স

বিপরীত ম্যাট্রিক্সএকটি ম্যাট্রিক্স বলা হয় যা, যখন একটি প্রদত্ত ম্যাট্রিক্স দ্বারা ডানে এবং বামে উভয়কে গুণ করা হয়, তখন পরিচয় ম্যাট্রিক্স দেয়।
ম্যাট্রিক্সের বিপরীত ম্যাট্রিক্সকে নির্দেশ করুন কিন্তুমাধ্যমে, তারপর সংজ্ঞা অনুযায়ী আমরা পাই:

কোথায় ইপরিচয় ম্যাট্রিক্স।
বর্গ ম্যাট্রিক্সডাকা অ বিশেষ (অধঃপতিত) যদি এর নির্ধারক শূন্যের সমান না হয়। অন্যথায়, এটি বলা হয় বিশেষ (অধঃপতন) বা একক.

একটি উপপাদ্য আছে: প্রতিটি অ-একবচন ম্যাট্রিক্স একটি বিপরীত ম্যাট্রিক্স আছে.

ইনভার্স ম্যাট্রিক্স খোঁজার অপারেশন বলা হয় আপিলম্যাট্রিক্স ম্যাট্রিক্স ইনভার্সন অ্যালগরিদম বিবেচনা করুন। একটি অ-একবচন ম্যাট্রিক্স দেওয়া যাক n-ম আদেশ:

যেখানে Δ = det ক ≠ 0.

বীজগাণিতিক উপাদান পরিপূরকম্যাট্রিক্স n-ম আদেশ কিন্তুম্যাট্রিক্সের নির্ধারক ( n-1)-ম অর্ডার ডিলিট করে প্রাপ্ত i-ম লাইন এবং j-ম্যাট্রিক্সের তম কলাম কিন্তু:

এর একটি তথাকথিত তৈরি করা যাক সংযুক্তম্যাট্রিক্স:

ম্যাট্রিক্সের সংশ্লিষ্ট উপাদানগুলির বীজগাণিতিক পরিপূরকগুলি কোথায় কিন্তু.
লক্ষ্য করুন যে ম্যাট্রিক্সের সারি উপাদানগুলির বীজগণিতিক পরিপূরক কিন্তুম্যাট্রিক্সের সংশ্লিষ্ট কলামে স্থাপন করা হয় Ã , অর্থাৎ ম্যাট্রিক্স একই সাথে স্থানান্তরিত হয়।
সমস্ত ম্যাট্রিক্স উপাদান বিভাজন Ã on Δ - ম্যাট্রিক্সের নির্ধারকের মান কিন্তু, আমরা ফলাফল হিসাবে বিপরীত ম্যাট্রিক্স পাই:

আমরা বিপরীত ম্যাট্রিক্সের বেশ কয়েকটি বিশেষ বৈশিষ্ট্য নোট করি:
1) একটি প্রদত্ত ম্যাট্রিক্সের জন্য কিন্তুএর বিপরীত ম্যাট্রিক্স একমাত্র;
2) যদি একটি বিপরীত ম্যাট্রিক্স থাকে, তাহলে ডান বিপরীতএবং বাম বিপরীতম্যাট্রিক্স এর সাথে মিলে যায়;
3) একটি বিশেষ (ক্ষয়প্রাপ্ত) বর্গ ম্যাট্রিক্সের একটি বিপরীত ম্যাট্রিক্স নেই।

বিপরীত ম্যাট্রিক্সের প্রধান বৈশিষ্ট্য:
1) বিপরীত ম্যাট্রিক্সের নির্ধারক এবং মূল ম্যাট্রিক্সের নির্ধারক পারস্পরিক;
2) বর্গাকার ম্যাট্রিক্সের গুণফলের বিপরীত ম্যাট্রিক্স বিপরীত ক্রমে নেওয়া ফ্যাক্টরের বিপরীত ম্যাট্রিক্সের গুণফলের সমান:

3) ট্রান্সপোজড ইনভার্স ম্যাট্রিক্স প্রদত্ত ট্রান্সপোজড ম্যাট্রিক্স থেকে ইনভার্স ম্যাট্রিক্সের সমান:

উদাহরণ প্রদত্ত একটির ম্যাট্রিক্স ইনভার্স গণনা করুন।

বীজগণিত সংযোজন এবং অপ্রাপ্তবয়স্ক

আসুন একটি তৃতীয় ক্রম নির্ধারক আছে: .

গৌণএই উপাদান অনুরূপ aijতৃতীয়-ক্রম নির্ণায়ককে বলা হয় দ্বিতীয়-ক্রম নির্ণায়ককে প্রদত্ত একটি থেকে প্রাপ্ত সারি এবং কলামটি মুছে ফেলার মাধ্যমে যার মধ্যে প্রদত্ত উপাদানটি দাঁড়িয়ে আছে, যেমন i-ম লাইন এবং j-ম কলাম। একটি প্রদত্ত উপাদানের সাথে সঙ্গতিপূর্ণ নাবালক aijআমরা চিহ্নিত করব M ij.

উদাহরণ স্বরূপ, গৌণ M12উপাদানের সাথে সম্পর্কিত একটি 12, একটি নির্ধারক হবে 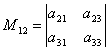, যা প্রদত্ত নির্ধারক থেকে 1ম সারি এবং 2য় কলাম মুছে ফেলার মাধ্যমে প্রাপ্ত হয়।

এইভাবে, যে সূত্রটি তৃতীয়-ক্রম নির্ধারক নির্ধারণ করে তা দেখায় যে এই নির্ধারকটি 1ম সারির উপাদান এবং তাদের সংশ্লিষ্ট অপ্রাপ্তবয়স্কদের গুণফলের সমষ্টির সমান; মৌল উপাদান অনুরূপ যখন একটি 12, "–" চিহ্ন দিয়ে নেওয়া হয়, যেমন এটা লেখা যেতে পারে

.

(1)

একইভাবে, কেউ দ্বিতীয় ক্রম এবং উচ্চতর আদেশের নির্ধারকদের জন্য অপ্রাপ্তবয়স্কদের সংজ্ঞা প্রবর্তন করতে পারে।

আরো একটি ধারণা চালু করা যাক.

বীজগণিত সংযোজনউপাদান aijনির্ধারককে এর গৌণ বলা হয় M ij(–1) i+j দ্বারা গুণিত।

বীজগাণিতিক উপাদান সংযোজন aijচিহ্নিত একটি ij.

সংজ্ঞা থেকে আমরা পাই যে একটি উপাদানের বীজগণিতীয় পরিপূরক এবং এর অপ্রধানের মধ্যে সংযোগটি সমতা দ্বারা প্রকাশ করা হয় একটি ij= (–1) i+j এম আইজি।

উদাহরণ স্বরূপ,

উদাহরণ।একটি নির্ধারক দেওয়া. অনুসন্ধান A 13, A 21, A 32.

এটি সহজে দেখা যায় যে উপাদানগুলির বীজগাণিতিক সংযোজন ব্যবহার করে, সূত্র (1) এভাবে লেখা যেতে পারে:

একইভাবে এই সূত্রে, যে কোনো সারি বা কলামের উপাদানের উপর নির্ধারকের পচন পাওয়া যায়।

উদাহরণস্বরূপ, 2য় সারির উপাদানগুলির উপর নির্ধারকের পচন নিম্নরূপ প্রাপ্ত করা যেতে পারে। নির্ধারকের সম্পত্তি 2 অনুসারে, আমাদের আছে:

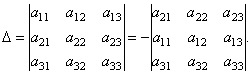
1ম সারির উপাদান দ্বারা প্রাপ্ত নির্ধারকটিকে প্রসারিত করা যাক।

.

(2)

এখান থেকে কারণ সূত্রে দ্বিতীয়-ক্রম নির্ধারক (2) উপাদানগুলির অপ্রাপ্তবয়স্ক একটি 21, একটি 22, একটি 23. এইভাবে, , i.e. আমরা 2য় সারির উপাদানগুলির দ্বারা নির্ধারকের প্রসারণ পেয়েছি।

একইভাবে, কেউ তৃতীয় সারির উপাদানগুলির উপর নির্ধারকের পচন পেতে পারে। নির্ধারকগুলির বৈশিষ্ট্য 1 ব্যবহার করে (স্থানান্তরে), কেউ দেখাতে পারে যে অনুরূপ সম্প্রসারণগুলি কলাম উপাদানগুলির পরিপ্রেক্ষিতে সম্প্রসারণের জন্যও বৈধ।

সুতরাং, নিম্নলিখিত উপপাদ্যটি সত্য।

উপপাদ্য (প্রদত্ত সারি বা কলামে নির্ধারকের সম্প্রসারণে)।নির্ধারক তার যেকোন সারি (বা কলাম) এবং তাদের বীজগণিতের পরিপূরক উপাদানগুলির গুণফলের সমষ্টির সমান।

উপরের সবগুলোই যে কোনো উচ্চতর অর্ডারের নির্ধারকদের জন্য সত্য।

উদাহরণ।

ইনভার্স ম্যাট্রিক্স

একটি বিপরীত ম্যাট্রিক্স ধারণা শুধুমাত্র জন্য প্রবর্তিত হয় বর্গ ম্যাট্রিক্স.

যদি একটি কএকটি বর্গ ম্যাট্রিক্স, তারপর বিপরীতএটির জন্য, একটি ম্যাট্রিক্স একটি ম্যাট্রিক্স নির্দেশিত ক-১এবং শর্ত সন্তুষ্ট. (এই সংজ্ঞাটি সংখ্যার গুণের সাথে সাদৃশ্য দ্বারা প্রবর্তিত হয়)

এই বিষয় ছাত্রদের মধ্যে সবচেয়ে ঘৃণ্য এক. আরও খারাপ, সম্ভবত, শুধুমাত্র নির্ধারক।

কৌশলটি হল যে বিপরীত উপাদানের ধারণাটি (এবং আমি এখন শুধু ম্যাট্রিক্সের কথা বলছি না) আমাদের গুণনের ক্রিয়াকে বোঝায়। এমনকি স্কুলের পাঠ্যক্রমে, গুণকে একটি জটিল ক্রিয়াকলাপ হিসাবে বিবেচনা করা হয়, এবং ম্যাট্রিক্স গুণন সাধারণত একটি পৃথক বিষয়, যার প্রতি আমার একটি সম্পূর্ণ অনুচ্ছেদ এবং একটি ভিডিও পাঠ রয়েছে।

আজ আমরা ম্যাট্রিক্স গণনার বিবরণে যাব না। শুধু মনে রাখবেন: ম্যাট্রিক্সগুলি কীভাবে চিহ্নিত করা হয়, কীভাবে তারা গুণিত হয় এবং এর থেকে কী অনুসরণ করা হয়।

পর্যালোচনা: ম্যাট্রিক্স গুণন

প্রথমত, আসুন স্বরলিপিতে একমত হই। একটি ম্যাট্রিক্স $A$ আকারের $\left[ m\times n \right]$ হল কেবলমাত্র $m$ সারি এবং $n$ কলাম সহ সংখ্যার একটি টেবিল:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) &... & ((a)_(1n)) \\ (( a)_(21) এবং ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(ম্যাট্রিক্স) \right])_(n)\]

ঘটনাক্রমে জায়গায় সারি এবং কলামগুলিকে বিভ্রান্ত না করার জন্য (আমাকে বিশ্বাস করুন, পরীক্ষায় আপনি একটি ইউনিটকে একটি ডিউস দিয়ে বিভ্রান্ত করতে পারেন - আমরা সেখানে কিছু লাইন সম্পর্কে কী বলতে পারি), কেবল ছবিটি দেখুন:

ম্যাট্রিক্স কোষের জন্য সূচক নির্ধারণ

কি হচ্ছে? যদি আমরা স্ট্যান্ডার্ড কোঅর্ডিনেট সিস্টেম $OXY$টিকে উপরের বাম কোণে রাখি এবং অক্ষগুলিকে নির্দেশ করি যাতে তারা পুরো ম্যাট্রিক্সকে আবৃত করে, তাহলে এই ম্যাট্রিক্সের প্রতিটি কক্ষ $\left(x;y \right) স্থানাঙ্কের সাথে অনন্যভাবে যুক্ত হতে পারে। $ - এটি হবে সারি নম্বর এবং কলাম নম্বর।

কেন স্থানাঙ্ক সিস্টেম ঠিক উপরের বাম কোণে স্থাপন করা হয়? হ্যাঁ, কারণ সেখান থেকেই আমরা যেকোনো লেখা পড়তে শুরু করি। এটা মনে রাখা খুব সহজ.

কেন $x$ অক্ষ নিচের দিকে নির্দেশ করছে এবং ডানদিকে নয়? আবার, এটা সহজ: স্ট্যান্ডার্ড কোঅর্ডিনেট সিস্টেম নিন ($x$ অক্ষ ডানদিকে যায়, $y$ অক্ষ উপরে যায়) এবং এটিকে ঘোরান যাতে এটি ম্যাট্রিক্সকে আবদ্ধ করে। এটি ঘড়ির কাঁটার দিকে 90 ডিগ্রি ঘূর্ণন - আমরা ছবিতে এর ফলাফল দেখতে পাচ্ছি।

সাধারণভাবে, আমরা ম্যাট্রিক্স উপাদানগুলির সূচকগুলি কীভাবে নির্ধারণ করতে হয় তা খুঁজে বের করেছি। এখন গুণন নিয়ে কাজ করা যাক।

সংজ্ঞা। ম্যাট্রিক্স $A=\left[ m\times n \right]$ এবং $B=\left[ n\times k \right]$, যখন প্রথম কলামের সংখ্যা দ্বিতীয় সারির সংখ্যার সাথে মেলে, সামঞ্জস্যপূর্ণ বলা হয়।

এটা সেই ক্রমে। কেউ অস্পষ্ট হতে পারে এবং বলতে পারে যে ম্যাট্রিক্স $A$ এবং $B$ একটি অর্ডারযুক্ত জোড়া গঠন করে $\left(A;B \right)$: যদি তারা এই ক্রমে সামঞ্জস্যপূর্ণ হয়, তাহলে $B এর প্রয়োজন নেই। $ এবং $A$, যারা. জোড়া $\left(B;A \right)$ও সামঞ্জস্যপূর্ণ।

শুধুমাত্র সামঞ্জস্যপূর্ণ ম্যাট্রিক্স গুণ করা যেতে পারে।

সংজ্ঞা। সামঞ্জস্যপূর্ণ ম্যাট্রিক্স $A=\left[ m\times n \right]$ এবং $B=\left[ n\times k \right]$ হল নতুন ম্যাট্রিক্স $C=\left[ m\times k \right ]$, যার উপাদান $((c)_(ij))$ সূত্র দ্বারা গণনা করা হয়:

\[(c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

অন্য কথায়: $C=A\cdot B$ ম্যাট্রিক্সের $((c)_(ij))$ উপাদান পেতে, আপনাকে প্রথম ম্যাট্রিক্সের $i$-সারি, $j$ নিতে হবে -দ্বিতীয় ম্যাট্রিক্সের তম কলাম, এবং তারপর এই সারি এবং কলাম থেকে জোড়া উপাদানে গুণ করুন। ফলাফল যোগ করুন.

হ্যাঁ, এটি একটি কঠোর সংজ্ঞা। বেশ কিছু তথ্য অবিলম্বে এটি থেকে অনুসরণ করে:

1. ম্যাট্রিক্স গুন হল, সাধারণভাবে বলতে গেলে, নন-কমিউটেটিভ: $A\cdot B\ne B\cdot A$;
2. যাইহোক, গুন হল সহযোগী: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. এবং এমনকি বিতরণকারী: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. এবং আবার বিতরণমূলক: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$।

গুণের বণ্টনকে বাম এবং ডান গুণকের যোগফলের জন্য আলাদাভাবে বর্ণনা করতে হয়েছিল শুধুমাত্র গুণের ক্রিয়াকলাপের অ-আদান-প্রদানের কারণে।

তা সত্ত্বেও, যদি দেখা যায় যে $A\cdot B=B\cdot A$, এই ধরনের ম্যাট্রিক্সগুলিকে পারমুটেবল বলা হয়।

সেখানে কিছু দ্বারা গুণ করা সমস্ত ম্যাট্রিক্সের মধ্যে বিশেষগুলি রয়েছে - যেগুলিকে, যে কোনও ম্যাট্রিক্স $A$ দ্বারা গুণ করা হলে, আবার $A$ দেয়:

সংজ্ঞা। $A\cdot E=A$ বা $E\cdot A=A$ হলে একটি ম্যাট্রিক্স $E$ কে আইডেন্টিটি বলা হয়। একটি বর্গ ম্যাট্রিক্স $A$ এর ক্ষেত্রে আমরা লিখতে পারি:

পরিচয় ম্যাট্রিক্স ম্যাট্রিক্স সমীকরণ সমাধানে একটি ঘন ঘন অতিথি। এবং সাধারণভাবে, ম্যাট্রিক্সের বিশ্বে ঘন ঘন অতিথি। :)

এবং এই $E$ এর কারণে, কেউ এমন সমস্ত গেম নিয়ে এসেছে যা পরবর্তী লেখা হবে।

একটি বিপরীত ম্যাট্রিক্স কি?

যেহেতু ম্যাট্রিক্স গুণন একটি খুব সময়সাপেক্ষ ক্রিয়াকলাপ (আপনাকে সারি এবং কলামগুলির একটি গুচ্ছ গুণ করতে হবে), একটি বিপরীত ম্যাট্রিক্সের ধারণাটিও খুব তুচ্ছ নয়। এবং এর কিছু ব্যাখ্যা প্রয়োজন।

মূল সংজ্ঞা

ঠিক আছে, সত্য জানার সময় এসেছে।

সংজ্ঞা। ম্যাট্রিক্স $B$ কে ম্যাট্রিক্স $A$ if এর বিপরীত বলা হয়

বিপরীত ম্যাট্রিক্সকে $((A)^(-1))$ (ডিগ্রির সাথে বিভ্রান্ত করা যাবে না!) দ্বারা চিহ্নিত করা হয়, তাই সংজ্ঞাটি এভাবে পুনরায় লেখা যেতে পারে:

এটা মনে হবে যে সবকিছু অত্যন্ত সহজ এবং পরিষ্কার। কিন্তু এই ধরনের সংজ্ঞা বিশ্লেষণ করার সময়, অবিলম্বে বেশ কয়েকটি প্রশ্ন উঠে আসে:

1. একটি বিপরীত ম্যাট্রিক্স সবসময় বিদ্যমান? এবং যদি সর্বদা না হয়, তবে কীভাবে নির্ধারণ করবেন: কখন এটি বিদ্যমান এবং কখন থাকে না?
2. এবং কে বলেছে যে এই জাতীয় ম্যাট্রিক্স ঠিক এক? যদি কিছু মূল ম্যাট্রিক্স $A$ এর জন্য বিপরীতের পুরো ভিড় থাকে তবে কী হবে?
3. এই সব "বিপরীত" দেখতে কেমন? এবং কিভাবে আপনি আসলে তাদের গণনা করবেন?

হিসাবের অ্যালগরিদম হিসাবে - আমরা এই সম্পর্কে একটু পরে কথা বলব। তবে আমরা এখনই বাকি প্রশ্নের উত্তর দেব। আসুন তাদের আলাদা দাবী-লেমা আকারে সাজাই।

মৌলিক বৈশিষ্ট্য

ম্যাট্রিক্স $A$ কেমন হওয়া উচিত তা দিয়ে শুরু করা যাক যাতে এটি $((A)^(-1))$ থাকে। এখন আমরা নিশ্চিত করব যে এই দুটি ম্যাট্রিক্স অবশ্যই বর্গক্ষেত্র এবং একই আকারের হতে হবে: $\left[ n\times n \right]$।

লেম্মা ঘ. একটি ম্যাট্রিক্স $A$ এবং এর বিপরীত $((A)^(-1))$ দেওয়া হয়েছে। তারপর এই উভয় ম্যাট্রিক্স বর্গাকার এবং একই ক্রম $n$।

প্রমাণ। সবকিছু সহজ. যাক ম্যাট্রিক্স $A=\left[ m\times n \right]$, $(A)^(-1))=\left[ a\times b \right]$। যেহেতু পণ্য $A\cdot ((A)^(-1))=E$ সংজ্ঞা অনুসারে বিদ্যমান, তাই ম্যাট্রিক্স $A$ এবং $((A)^(-1))$ সেই ক্রমে সামঞ্জস্যপূর্ণ:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( সারিবদ্ধ)\]

এটি ম্যাট্রিক্স গুণন অ্যালগরিদমের একটি সরাসরি পরিণতি: সহগ $n$ এবং $a$ হল "ট্রানজিট" এবং অবশ্যই সমান হতে হবে৷

একই সময়ে, বিপরীত গুণকেও সংজ্ঞায়িত করা হয়েছে: $((A)^(-1))\cdot A=E$, তাই ম্যাট্রিক্স $((A)^(-1))$ এবং $A$ হল এই ক্রমেও সামঞ্জস্যপূর্ণ:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( সারিবদ্ধ)\]

সুতরাং, সাধারণতা না হারিয়ে, আমরা ধরে নিতে পারি যে $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$। যাইহোক, $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$ এর সংজ্ঞা অনুসারে, তাই ম্যাট্রিক্সের মাত্রা ঠিক একই:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

সুতরাং দেখা যাচ্ছে যে তিনটি ম্যাট্রিক্স - $A$, $(A)^(-1))$ এবং $E$ - আকারে $\left[ n\times n \right]$। লেমা প্রমাণিত।

ওয়েল, যে ইতিমধ্যেই ভাল. আমরা দেখতে পাচ্ছি যে শুধুমাত্র বর্গ ম্যাট্রিক্সগুলি বিপরীতমুখী। এখন নিশ্চিত করা যাক যে বিপরীত ম্যাট্রিক্স সর্বদা একই।

লেমা 2। একটি ম্যাট্রিক্স $A$ এবং এর বিপরীত $((A)^(-1))$ দেওয়া হয়েছে। তাহলে এই বিপরীত ম্যাট্রিক্সটি অনন্য।

প্রমাণ। এর বিপরীত থেকে শুরু করা যাক: ম্যাট্রিক্স $A$-এর অন্তত দুটি ইনস্ট্যান্স ইনভার্স আছে — $B$ এবং $C$। তারপর, সংজ্ঞা অনুসারে, নিম্নলিখিত সমতাগুলি সত্য:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \শেষ(সারিবদ্ধ)\]

লেমা 1 থেকে আমরা উপসংহারে পৌঁছেছি যে চারটি ম্যাট্রিক্স $A$, $B$, $C$ এবং $E$ একই ক্রমে বর্গক্ষেত্র: $\left[ n\times n \right]$। অতএব, পণ্য সংজ্ঞায়িত করা হয়:

যেহেতু ম্যাট্রিক্স গুণন সহযোগী (কিন্তু কম্যুটেটিভ নয়!), আমরা লিখতে পারি:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \শেষ(সারিবদ্ধ)\]

আমরা একমাত্র সম্ভাব্য বিকল্প পেয়েছি: বিপরীত ম্যাট্রিক্সের দুটি কপি সমান। লেমা প্রমাণিত।

উপরের যুক্তিটি প্রায় মৌখিকভাবে সমস্ত বাস্তব সংখ্যা $b\ne 0$ এর বিপরীত উপাদানের স্বতন্ত্রতার প্রমাণের পুনরাবৃত্তি করে। একমাত্র উল্লেখযোগ্য সংযোজন হল ম্যাট্রিক্সের মাত্রা বিবেচনা করা।

যাইহোক, আমরা এখনও কিছু জানি না যে কোনও বর্গ ম্যাট্রিক্স ইনভার্টেবল কিনা। এখানে নির্ধারক আমাদের সাহায্যে আসে - এটি সমস্ত বর্গ ম্যাট্রিকের জন্য একটি মূল বৈশিষ্ট্য।

লেমা 3। একটি ম্যাট্রিক্স $A$ দেওয়া হয়েছে৷ যদি ম্যাট্রিক্স $((A)^(-1))$ এর বিপরীতে থাকে, তাহলে মূল ম্যাট্রিক্সের নির্ধারকটি অশূন্য:

\[\বাম| একটি \right|\ne 0\]

প্রমাণ। আমরা ইতিমধ্যেই জানি যে $A$ এবং $((A)^(-1))$ হল $\left[ n\times n \right]$ আকারের বর্গ ম্যাট্রিক্স। অতএব, তাদের প্রত্যেকের জন্য নির্ধারক গণনা করা সম্ভব: $\left| একটি \right|$ এবং $\left| ((A)^(-1)) \right|$। যাইহোক, পণ্যের নির্ধারক নির্ধারকদের গুণফলের সমান:

\[\বাম| A\cdot B \right|=\left| একটি \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| একটি \right|\cdot \left| ((A)^(-1)) \right|\]

কিন্তু $A\cdot ((A)^(-1))=E$ এর সংজ্ঞা অনুসারে, এবং $E$ এর নির্ধারক সর্বদা 1 এর সমান, তাই

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \বাম| A\cdot ((A)^(-1)) \right|=\left| E\right|; \\ & \বাম| একটি \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \শেষ(সারিবদ্ধ)\]

দুটি সংখ্যার গুণফল শুধুমাত্র একটির সমান হয় যদি এই সংখ্যাগুলির প্রতিটি শূন্য থেকে আলাদা হয়:

\[\বাম| একটি \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

সুতরাং দেখা যাচ্ছে যে $\left| একটি \right|\ne 0$। লেমা প্রমাণিত।

আসলে, এই প্রয়োজনীয়তা বেশ যৌক্তিক। এখন আমরা বিপরীত ম্যাট্রিক্স খুঁজে বের করার জন্য অ্যালগরিদম বিশ্লেষণ করব - এবং এটি সম্পূর্ণরূপে পরিষ্কার হয়ে যাবে কেন, নীতিগতভাবে, শূন্য নির্ধারক সহ কোনও বিপরীত ম্যাট্রিক্স থাকতে পারে না।

কিন্তু প্রথমে, আসুন একটি "সহায়ক" সংজ্ঞা প্রণয়ন করি:

সংজ্ঞা। ডিজেনারেট ম্যাট্রিক্স হল $\left[ n\times n \right]$ এর একটি বর্গ ম্যাট্রিক্স যার নির্ণায়ক শূন্য।

সুতরাং, আমরা দৃঢ়ভাবে বলতে পারি যে কোনো ইনভার্টেবল ম্যাট্রিক্স ননডিজেনারেট।

কিভাবে ইনভার্স ম্যাট্রিক্স খুঁজে বের করতে হয়

এখন আমরা বিপরীত ম্যাট্রিক্স খুঁজে বের করার জন্য একটি সার্বজনীন অ্যালগরিদম বিবেচনা করব। সাধারণভাবে, দুটি সাধারণভাবে গৃহীত অ্যালগরিদম রয়েছে এবং আমরা আজ দ্বিতীয়টিকেও বিবেচনা করব।

যেটিকে এখন বিবেচনা করা হবে তা $\left[ 2\times 2 \right]$ এবং - $\left[ 3\times 3 \right]$ আকারের ম্যাট্রিক্সের জন্য খুবই দক্ষ। কিন্তু $\left[ 4\times 4 \right]$ থেকে শুরু করে এটি ব্যবহার না করাই ভালো। কেন- এখন সব বুঝবে।

বীজগণিত সংযোজন

প্রস্তুত হও. এখন ব্যথা হবে। না, চিন্তা করবেন না: একটি স্কার্টে একটি সুন্দর নার্স, লেইস সহ স্টকিংস আপনার কাছে আসে না এবং আপনাকে নিতম্বে একটি ইনজেকশন দেবে না। সবকিছুই অনেক বেশি সহজবোধ্য: বীজগাণিতিক সংযোজন এবং মহারাজ "ইউনিয়ন ম্যাট্রিক্স" আপনার কাছে আসছে।

এর প্রধান এক সঙ্গে শুরু করা যাক. $A=\left[ n\times n \right]$ এর একটি বর্গ ম্যাট্রিক্স থাকুক যার উপাদানগুলির নাম $((a)_(ij))$। তারপর, এই জাতীয় প্রতিটি উপাদানের জন্য, কেউ একটি বীজগাণিতিক পরিপূরক সংজ্ঞায়িত করতে পারে:

সংজ্ঞা। $A=\left ম্যাট্রিক্সের $i$-তম সারিতে এবং $j$-th কলামে $((a)_(ij))$ মৌলের $((A)_(ij))$ এর বীজগণিতিক পরিপূরক [ n \times n \right]$ হল ফর্মের একটি নির্মাণ

\[(A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

যেখানে $M_(ij)^(*)$ হল একই $i$-th সারি এবং $j$-th কলাম মুছে দিয়ে আসল $A$ থেকে প্রাপ্ত ম্যাট্রিক্সের নির্ধারক।

আবার। স্থানাঙ্ক $\left(i;j \right)$ সহ ম্যাট্রিক্স উপাদানের বীজগাণিতিক পরিপূরক $((A)_(ij))$ হিসাবে চিহ্নিত করা হয় এবং স্কিম অনুযায়ী গণনা করা হয়:

1. প্রথমে, আমরা মূল ম্যাট্রিক্স থেকে $i$-রো এবং $j$-th কলাম মুছে ফেলি। আমরা একটি নতুন বর্গ ম্যাট্রিক্স পাই, এবং আমরা এর নির্ধারককে $M_(ij)^(*)$ হিসাবে চিহ্নিত করি।
2. তারপরে আমরা এই নির্ণায়কটিকে $((\left(-1 \right))^(i+j))$ দিয়ে গুণ করি - প্রথমে এই অভিব্যক্তিটি মনের মতো মনে হতে পারে, কিন্তু আসলে আমরা $ এর সামনের চিহ্নটি খুঁজে পাই M_(ij)^(*) $।
3. আমরা গণনা করি - আমরা একটি নির্দিষ্ট সংখ্যা পাই। সেগুলো. বীজগাণিতিক সংযোজন শুধুমাত্র একটি সংখ্যা, কিছু নতুন ম্যাট্রিক্স নয়, ইত্যাদি।

$M_(ij)^(*)$ ম্যাট্রিক্সকে নিজেই $((a)_(ij))$ মৌলের পরিপূরক মাইনর বলা হয়। এবং এই অর্থে, বীজগাণিতিক পরিপূরকের উপরোক্ত সংজ্ঞাটি আরও জটিল সংজ্ঞার একটি বিশেষ ক্ষেত্রে - যেটি আমরা নির্ধারক সম্পর্কে পাঠে বিবেচনা করেছি।

গুরুত্বপূর্ণ তথ্য. প্রকৃতপক্ষে, "প্রাপ্তবয়স্ক" গণিতে, বীজগণিত সংযোজনগুলি নিম্নরূপ সংজ্ঞায়িত করা হয়েছে:

1. আমরা একটি বর্গ ম্যাট্রিক্সে $k$ সারি এবং $k$ কলাম নিই। তাদের সংযোগস্থলে, আমরা $\left[ k\times k \right]$ আকারের একটি ম্যাট্রিক্স পাই — এর নির্ণায়ককে বলা হয় একটি মাইনর অফ অর্ডার $k$ এবং $((M)_(k))$ দ্বারা চিহ্নিত করা হয়।
2. তারপর আমরা এই "নির্বাচিত" $k$ সারি এবং $k$ কলামগুলি ক্রস আউট করি। আবার, আমরা একটি বর্গ ম্যাট্রিক্স পাই - এর নির্ধারককে পরিপূরক মাইনর বলা হয় এবং $M_(k)^(*)$ দ্বারা চিহ্নিত করা হয়।
3. $M_(k)^(*)$ কে $((\left(-1 \right))^(t))$ দিয়ে গুণ করুন, যেখানে $t$ হল (এখন মনোযোগ দিন!) সমস্ত নির্বাচিত সারির সংখ্যার যোগফল। এবং কলাম এটি বীজগণিত সংযোজন হবে।

তৃতীয় ধাপে একবার দেখুন: আসলে $2k$ পদের যোগফল আছে! আরেকটি বিষয় হল যে $k=1$ এর জন্য আমরা শুধুমাত্র 2টি পদ পাই - এইগুলি একই $i+j$ হবে - $((a)_(ij))$ উপাদানটির "স্থানাঙ্ক", যার জন্য আমরা একটি বীজগণিত পরিপূরক খুঁজছেন.

তাই আজ আমরা একটি সামান্য সরলীকৃত সংজ্ঞা ব্যবহার. কিন্তু আমরা পরে দেখব, এটি যথেষ্ট হবে। আরো অনেক গুরুত্বপূর্ণ নিম্নলিখিত:

সংজ্ঞা। ইউনিয়ন ম্যাট্রিক্স $S$ থেকে বর্গ ম্যাট্রিক্স $A=\left[ n\times n \right]$ হল $\left[ n\times n \right]$ আকারের একটি নতুন ম্যাট্রিক্স, যা $A$ থেকে প্রাপ্ত হয় বীজগণিতের পরিপূরক $((A)_(ij))$ দ্বারা $((a)_(ij))$ প্রতিস্থাপন করে:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) এবং ((A)_(12)) &... & ((A)_(1n)) \\ (( A)_(21) এবং ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \ right]\]

এই সংজ্ঞাটি উপলব্ধি করার মুহুর্তে প্রথম যে চিন্তাটি উদ্ভূত হয় তা হল "এটি আপনাকে মোট কতটা গণনা করতে হবে!" শিথিল করুন: আপনাকে গণনা করতে হবে, তবে এত বেশি নয়। :)

আচ্ছা, এই সব খুব সুন্দর, কিন্তু এটা কেন প্রয়োজন? কিন্তু কেন.

প্রধান উপপাদ্য

একটু পিছিয়ে যাই। মনে রাখবেন, লেমা 3 বলেছে যে একটি ইনভার্টেবল ম্যাট্রিক্স $A$ সর্বদা অ-একবচন (অর্থাৎ, এর নির্ধারক হল অ-শূন্য: $\left| A \right|\ne 0$)।

সুতরাং, কথোপকথনটিও সত্য: যদি ম্যাট্রিক্স $A$ ক্ষয়প্রাপ্ত না হয়, তবে এটি সর্বদা বিপরীতমুখী। এবং এমনকি একটি অনুসন্ধান স্কিম $((A)^(-1))$ আছে৷ এটা দেখ:

বিপরীত ম্যাট্রিক্স উপপাদ্য। একটি বর্গ ম্যাট্রিক্স $A=\left[ n\times n \right]$ দেওয়া যাক, এবং এর নির্ধারক হল অশূন্য: $\left| একটি \right|\ne 0$। তারপরে বিপরীত ম্যাট্রিক্স $((A)^(-1))$ বিদ্যমান এবং সূত্র দ্বারা গণনা করা হয়:

\[(A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

এবং এখন - সব একই, কিন্তু স্পষ্ট হস্তাক্ষর মধ্যে. বিপরীত ম্যাট্রিক্স খুঁজে পেতে, আপনার প্রয়োজন:

1. নির্ধারক $\left| গণনা করুন একটি \right|$ এবং নিশ্চিত করুন যে এটি অ-শূন্য।
2. ইউনিয়ন ম্যাট্রিক্স $S$ কম্পাইল করুন, যেমন 100500 বীজগণিত সংযোজন $((A)_(ij))$ গণনা করুন এবং সেগুলিকে $((a)_(ij))$ বসান।
3. এই ম্যাট্রিক্সটি $S$ স্থানান্তর করুন এবং তারপর এটিকে কিছু সংখ্যা $q=(1)/(\left| A \right|)\;$ দিয়ে গুণ করুন।

এবং এটাই! বিপরীত ম্যাট্রিক্স $((A)^(-1))$ পাওয়া যায়। আসুন উদাহরণ দেখি:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

সমাধান। এর বিপরীততা পরীক্ষা করা যাক. আসুন নির্ধারক গণনা করা যাক:

\[\বাম| একটি \right|=\left| \begin(ম্যাট্রিক্স) 3 এবং 1 \\ 5 এবং 2 \\\end(ম্যাট্রিক্স) \right|=3\cdot 2-1\cdot 5=6-5=1\]

নির্ধারক শূন্য থেকে ভিন্ন। সুতরাং ম্যাট্রিক্সটি বিপরীতমুখী। আসুন একটি ইউনিয়ন ম্যাট্রিক্স তৈরি করি:

আসুন বীজগাণিতিক সংযোজন গণনা করি:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\right|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\right|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\right|=3. \\ \শেষ(সারিবদ্ধ)\]

মনোযোগ দিন: নির্ধারক |2|, |5|, |1| এবং |3| $\left[ 1\times 1 \right]$ আকারের ম্যাট্রিক্সের নির্ধারক, মডিউল নয়। সেগুলো. যদি নির্ধারকগুলিতে নেতিবাচক সংখ্যা থাকে তবে "বিয়োগ" অপসারণের প্রয়োজন নেই।

মোট, আমাদের ইউনিয়ন ম্যাট্রিক্স এই মত দেখায়:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(অ্যারে) \right])^(T))=\left[ শুরু (অ্যারে)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(অ্যারে) \right]\]

ঠিক আছে এখন সব শেষ। সমস্যা সমাধান.

উত্তর. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \ right]$

একটি কাজ. বিপরীত ম্যাট্রিক্স খুঁজুন:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \ right] \]

সমাধান। আবার, আমরা নির্ধারক বিবেচনা করি:

\[\begin(align) & \left| \begin(অ্যারে)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matrix) ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

নির্ধারকটি শূন্য থেকে আলাদা - ম্যাট্রিক্সটি বিপরীতমুখী। কিন্তু এখন এটি সবচেয়ে ছোট হবে: আপনাকে গণনা করতে হবে 9 (নয়টি, অভিশাপ!) বীজগণিত সংযোজন। এবং তাদের প্রত্যেকটিতে $\left[ 2\times 2 \right]$ কোয়ালিফায়ার থাকবে। উড়ে গেছে:

\[\begin(ম্যাট্রিক্স) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(ম্যাট্রিক্স) 2 & -1 \\ 0 & 1 \\\end(ম্যাট্রিক্স) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(ম্যাট্রিক্স) 0 & -1 \\ 1 & 1 \\\end(ম্যাট্রিক্স) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33)) =((\left(-1 \right))^(3+3))\cdot \left| \begin(ম্যাট্রিক্স) 1 & -1 \\ 0 & 2 \\\end(ম্যাট্রিক্স) \right|=2; \\ \end(ম্যাট্রিক্স)\]

সংক্ষেপে, ইউনিয়ন ম্যাট্রিক্স এই মত দেখাবে:

অতএব, বিপরীত ম্যাট্রিক্স হবে:

\[(A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 এবং 1 এবং 2 \\\end(ম্যাট্রিক্স) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(অ্যারে) \right]\]

ভাল, যে সব. এখানে উত্তর আছে.

উত্তর. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \ right ]$

আপনি দেখতে পাচ্ছেন, প্রতিটি উদাহরণের শেষে, আমরা একটি চেক সম্পাদন করেছি। এই বিষয়ে, একটি গুরুত্বপূর্ণ নোট:

চেক করতে অলস হবেন না। আসল ম্যাট্রিক্সকে পাওয়া বিপরীত দ্বারা গুণ করুন - আপনার $E$ পাওয়া উচিত।

এই চেকটি সম্পাদন করা আরও সহজ এবং দ্রুততর গণনায় একটি ত্রুটি সন্ধান করার চেয়ে, যখন, উদাহরণস্বরূপ, আপনি একটি ম্যাট্রিক্স সমীকরণ সমাধান করেন।

বিকল্প উপায়

আমি যেমন বলেছি, ইনভার্স ম্যাট্রিক্স উপপাদ্য $\left[ 2\times 2 \right]$ এবং $\left[ 3\times 3 \right]$ (পরবর্তী ক্ষেত্রে, এটি এতটা "মহান" নয় আর)। ”), তবে বড় ম্যাট্রিক্সের জন্য, দুঃখ শুরু হয়।

কিন্তু চিন্তা করবেন না: একটি বিকল্প অ্যালগরিদম রয়েছে যা $\left[ 10\times 10 \right]$ ম্যাট্রিক্সের জন্যও শান্তভাবে বিপরীতটি খুঁজে পেতে ব্যবহার করা যেতে পারে। কিন্তু, প্রায়শই ক্ষেত্রে, এই অ্যালগরিদম বিবেচনা করার জন্য, আমাদের একটু তাত্ত্বিক পটভূমি প্রয়োজন।

প্রাথমিক রূপান্তর

ম্যাট্রিক্সের বিভিন্ন রূপান্তরগুলির মধ্যে, বেশ কয়েকটি বিশেষ রয়েছে - সেগুলিকে প্রাথমিক বলা হয়। ঠিক তিনটি রূপান্তর আছে:

1. গুণ. আপনি $i$-th সারি (কলাম) নিতে পারেন এবং এটিকে $k\ne 0$ দিয়ে গুণ করতে পারেন;
2. সংযোজন. $i$-তম সারিতে (কলাম) যোগ করুন অন্য যেকোন $j$-তম সারি (কলাম) যেকোন সংখ্যা দ্বারা গুণিত $k\ne 0$ (অবশ্যই, $k=0$ও সম্ভব, কিন্তু এর অর্থ কী যে? ?যদিও কিছুই পরিবর্তন হবে না)।
3. পারমুটেশন। $i$-th এবং $j$-th সারি (কলাম) নিন এবং তাদের অদলবদল করুন।

কেন এই রূপান্তরগুলিকে প্রাথমিক বলা হয় (বড় ম্যাট্রিসের জন্য এগুলি এত প্রাথমিক দেখায় না) এবং কেন তাদের মধ্যে কেবল তিনটি রয়েছে - এই প্রশ্নগুলি আজকের পাঠের সুযোগের বাইরে। অতএব, আমরা বিস্তারিত যেতে হবে না.

আরেকটি বিষয় গুরুত্বপূর্ণ: আমাদের সংশ্লিষ্ট ম্যাট্রিক্সে এই সমস্ত বিকৃতি সম্পাদন করতে হবে। হ্যাঁ, হ্যাঁ, আপনি ঠিক শুনেছেন। এখন আরও একটি সংজ্ঞা থাকবে - আজকের পাঠের শেষটি।

সংযুক্ত ম্যাট্রিক্স

অবশ্যই স্কুলে আপনি যোগ পদ্ধতি ব্যবহার করে সমীকরণের সিস্টেমগুলি সমাধান করেছেন। ঠিক আছে, সেখানে, একটি লাইন থেকে আরেকটি বিয়োগ করুন, কিছু লাইনকে একটি সংখ্যা দ্বারা গুণ করুন - এটিই সব।

সুতরাং: এখন সবকিছু একই হবে, তবে ইতিমধ্যে "প্রাপ্তবয়স্ক উপায়ে"। প্রস্তুত?

সংজ্ঞা। ম্যাট্রিক্স $A=\left[ n\times n \right]$ এবং আইডেন্টিটি ম্যাট্রিক্স $E$ একই আকারের $n$ দেওয়া যাক। তারপর সংশ্লিষ্ট ম্যাট্রিক্স $\left[ A\left| ই \ ডান। \right]$ হল একটি নতুন $\left[ n\times 2n \right]$ ম্যাট্রিক্স যা দেখতে এইরকম:

\[\left[ A\left| ই \ ডান। \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) এবং ((a)_(12)) &... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\(a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

সংক্ষেপে, আমরা ম্যাট্রিক্স $A$ নিই, ডানদিকে আমরা এটিকে প্রয়োজনীয় আকারের পরিচয় ম্যাট্রিক্স $E$ বরাদ্দ করি, আমরা সৌন্দর্যের জন্য একটি উল্লম্ব বার দিয়ে সেগুলিকে আলাদা করি - এখানে আপনার কাছে সংযুক্ত রয়েছে। :)

ধরা কি? এবং এখানে কি:

উপপাদ্য। ম্যাট্রিক্স $A$ ইনভার্টেবল হতে দিন। সন্নিহিত ম্যাট্রিক্স $\left[ A\left| বিবেচনা করুন ই \ ডান। \right]$। ব্যবহার করলে প্রাথমিক স্ট্রিং রূপান্তরএটিকে $\left[ E\left| ফর্মে আনুন B \ ডান। \right]$, যেমন ডানদিকে $A$ ম্যাট্রিক্স $E$ থেকে প্রাপ্ত করার জন্য সারিগুলিকে গুণ, বিয়োগ এবং পুনর্বিন্যাস করে, তারপর বাম দিকে প্রাপ্ত ম্যাট্রিক্স $B$ হল $A$-এর বিপরীত:

\[\left[ A\left| ই \ ডান। \right]\থেকে \বামে[ E\বাম | B \ ডান। \right]\Rightarrow B=((A)^(-1))\]

এটা যে সহজ! সংক্ষেপে, ইনভার্স ম্যাট্রিক্স খুঁজে বের করার জন্য অ্যালগরিদম এইরকম দেখায়:

1. সংশ্লিষ্ট ম্যাট্রিক্স লিখুন $\left[ A\left| ই \ ডান। \right]$;
2. প্রাথমিক স্ট্রিং রূপান্তরগুলি সম্পাদন করুন যতক্ষণ না $A$ এর পরিবর্তে $E$ প্রদর্শিত হয়;
3. অবশ্যই, কিছু বাম দিকেও প্রদর্শিত হবে - একটি নির্দিষ্ট ম্যাট্রিক্স $B$। এই বিপরীত হবে;
4. লাভ! :)

অবশ্যই, কাজ করার চেয়ে অনেক সহজ বলা. তাহলে আসুন কয়েকটি উদাহরণ দেখি: $\left[ 3\times 3 \right]$ এবং $\left[ 4\times 4 \right]$ মাপের জন্য।

একটি কাজ. বিপরীত ম্যাট্রিক্স খুঁজুন:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \ right]\ ]

সমাধান। আমরা সংযুক্ত ম্যাট্রিক্স রচনা করি:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 এবং 1 \\\শেষ(অ্যারে) \right]\]

যেহেতু মূল ম্যাট্রিক্সের শেষ কলামটি দিয়ে পূর্ণ, বাকি থেকে প্রথম সারিটি বিয়োগ করুন:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matrix)\to \\ & \to\left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(অ্যারে) \right] \\ \end(সারিবদ্ধ)\]

প্রথম লাইন ছাড়া আর কোন ইউনিট নেই। কিন্তু আমরা এটি স্পর্শ করি না, অন্যথায় সদ্য সরানো ইউনিটগুলি তৃতীয় কলামে "গুণ" করতে শুরু করবে।

কিন্তু আমরা শেষ লাইন থেকে দ্বিতীয় লাইনটি দুবার বিয়োগ করতে পারি - আমরা নীচের বাম কোণে একটি ইউনিট পাই:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right]\begin(matrix) \\ \downarrow \\ -2 \\\end(matrix)\to \\ & \left [ শুরু (অ্যারে)(আরআরআর & 1 \\\end(অ্যারে) \right] \\ \end(সারিবদ্ধ)\]

এখন আমরা প্রথম থেকে শেষ সারি এবং দ্বিতীয় থেকে দুবার বিয়োগ করতে পারি - এইভাবে আমরা প্রথম কলামটিকে "শূন্য" করব:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(অ্যারে) \right]\begin(matrix) -1 \\ -2 \\ \\uparrow \\\end(matrix)\to \\ & \ বাম দিকে[ শুরু করুন(অ্যারে)(আরআরআর & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

দ্বিতীয় সারিটিকে −1 দ্বারা গুণ করুন এবং তারপর প্রথম থেকে 6 বার বিয়োগ করুন এবং শেষটিতে 1 বার যোগ করুন:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(অ্যারে) \right]\begin(matrix) \\ \left| \cdot \left(-1 \right) \right. \\ \\\end(ম্যাট্রিক্স)\ থেকে \\ & \ থেকে \left[ শুরু (অ্যারে)(rrr|rrr) 0 এবং 6 এবং 1 এবং 0 এবং 2 এবং -1 \\ 0 এবং 1 এবং 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -6 \\ updownarrow \\ +1 \\\end (ম্যাট্রিক্স) \\ থেকে \\ & \ থেকে \left[ শুরু (অ্যারে)(আরআরআর \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \right] \\ \end(align)\]

এটি শুধুমাত্র লাইন 1 এবং 3 অদলবদল করতে রয়ে গেছে:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 এবং 32 এবং -13 \\\শেষ(অ্যারে) \right]\]

প্রস্তুত! ডানদিকে প্রয়োজনীয় বিপরীত ম্যাট্রিক্স রয়েছে।

উত্তর. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \ right ]$

একটি কাজ. বিপরীত ম্যাট্রিক্স খুঁজুন:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\শেষ(ম্যাট্রিক্স) \ ডান]\]

সমাধান। আবার আমরা সংযুক্ত একটি রচনা:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(অ্যারে) \right]\]

আসুন একটু ধার করি, এখন আমাদের কত গুনতে হবে তা নিয়ে চিন্তা করুন ... এবং গণনা শুরু করুন। শুরুতে, আমরা সারি 2 এবং 3 থেকে সারি 1 বিয়োগ করে প্রথম কলামটিকে "শূন্য" করি:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(অ্যারে) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

আমরা 2-4 লাইনে অনেকগুলি "মাইনাস" লক্ষ্য করি। তিনটি সারিকে −1 দ্বারা গুণ করুন, এবং তারপর বাকি থেকে সারি 3 বিয়োগ করে তৃতীয় কলামটি বার্ন করুন:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(অ্যারে) \right]\begin(ম্যাট্রিক্স) \\ \left| \cdot \left(-1 \right) \right. \\ \বাম| \cdot \left(-1 \right) \right. \\ \বাম| \cdot \left(-1 \right) \right. \\\end(ম্যাট্রিক্স)\ থেকে \\ & \ থেকে \left[ শুরু (অ্যারে)(rrrr|rrrr) 1 এবং 4 এবং 2 এবং 3 এবং 1 এবং 0 এবং 0 এবং 0 \\ 0 এবং 6 এবং 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (অ্যারে) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrix)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

এখন মূল ম্যাট্রিক্সের শেষ কলামটি "ভাজার" সময়: বাকি থেকে সারি 4 বিয়োগ করুন:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(অ্যারে) ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

চূড়ান্ত রোল: সারি 1 এবং 3 থেকে সারি 2 বিয়োগ করে দ্বিতীয় কলামটি "বার্ন আউট" করুন:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

এবং আবার, বাম দিকে পরিচয় ম্যাট্রিক্স, তাই ডানদিকে বিপরীত। :)

উত্তর. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(ম্যাট্রিক্স) \right]$

ঠিক আছে এখন সব শেষ। নিজেই পরীক্ষা করুন - আমি বাতিল হয়েছি। :)

nম ক্রমটির একটি বর্গ ম্যাট্রিক্স থাকুক

ম্যাট্রিক্স A-1 বলা হয় বিপরীত ম্যাট্রিক্সম্যাট্রিক্স A এর ক্ষেত্রে, যদি A * A -1 = E হয়, যেখানে E হল nম ক্রমটির পরিচয় ম্যাট্রিক্স।

পরিচয় ম্যাট্রিক্স- এই ধরনের একটি বর্গাকার ম্যাট্রিক্স, যাতে প্রধান তির্যক বরাবর সমস্ত উপাদান, উপরের বাম কোণ থেকে নীচের ডান কোণে চলে যায়, এবং বাকিগুলি শূন্য, উদাহরণস্বরূপ:

বিপরীত ম্যাট্রিক্সবিদ্যমান থাকতে পারে শুধুমাত্র বর্গ ম্যাট্রিক্সের জন্যসেগুলো. সারি এবং কলামের একই সংখ্যক ম্যাট্রিক্সের জন্য।

ইনভার্স ম্যাট্রিক্স এক্সিস্টেন্স কন্ডিশন থিওরেম

একটি ম্যাট্রিক্সের একটি বিপরীত ম্যাট্রিক্স থাকার জন্য, এটি ননডিজেনারেট হওয়া আবশ্যক এবং যথেষ্ট।

ম্যাট্রিক্স A = (A1, A2,...A n) বলা হয় অধঃপতিতযদি কলাম ভেক্টর রৈখিকভাবে স্বাধীন হয়। একটি ম্যাট্রিক্সের রৈখিকভাবে স্বাধীন কলাম ভেক্টরের সংখ্যাকে ম্যাট্রিক্সের র‌্যাঙ্ক বলা হয়। অতএব, আমরা বলতে পারি যে একটি বিপরীত ম্যাট্রিক্সের অস্তিত্বের জন্য, এটি প্রয়োজনীয় এবং যথেষ্ট যে ম্যাট্রিক্সের র‌্যাঙ্ক তার মাত্রার সমান, যেমন r = n.

বিপরীত ম্যাট্রিক্স খোঁজার জন্য অ্যালগরিদম

1. গাউস পদ্ধতিতে সমীকরণের সিস্টেমগুলি সমাধানের জন্য টেবিলে ম্যাট্রিক্স A লিখুন এবং ডানদিকে (সমীকরণের ডান অংশের জায়গায়) এটিতে ম্যাট্রিক্স E নির্ধারণ করুন।
2. জর্ডান রূপান্তর ব্যবহার করে, একক কলাম সমন্বিত একটি ম্যাট্রিক্স এ ম্যাট্রিক্স এ আনুন; এই ক্ষেত্রে, একই সাথে ম্যাট্রিক্স E রূপান্তর করা প্রয়োজন।
3. যদি প্রয়োজন হয়, শেষ টেবিলের সারি (সমীকরণ) পুনর্বিন্যাস করুন যাতে পরিচয় ম্যাট্রিক্স E মূল টেবিলের ম্যাট্রিক্স A-এর অধীনে পাওয়া যায়।
4. বিপরীত ম্যাট্রিক্স A -1 লিখুন, যা মূল টেবিলের ম্যাট্রিক্স E এর অধীনে শেষ টেবিলে রয়েছে।

উদাহরণ 1

ম্যাট্রিক্স A-এর জন্য, বিপরীত ম্যাট্রিক্স A -1 খুঁজুন

সমাধান: আমরা ম্যাট্রিক্স A লিখে রাখি এবং ডানদিকে আমরা পরিচয় ম্যাট্রিক্স E নির্ধারণ করি। জর্ডান রূপান্তর ব্যবহার করে, আমরা ম্যাট্রিক্স A-কে আইডেন্টিটি ম্যাট্রিক্স E-তে কমিয়ে দিই। গণনাগুলি সারণি 31.1 এ দেখানো হয়েছে।

আসল ম্যাট্রিক্স A এবং বিপরীত ম্যাট্রিক্স A -1 গুণ করে গণনার সঠিকতা পরীক্ষা করা যাক।

ম্যাট্রিক্স গুণনের ফলে, পরিচয় ম্যাট্রিক্স প্রাপ্ত হয়। অতএব, গণনা সঠিক।

উত্তর:

ম্যাট্রিক্স সমীকরণের সমাধান

ম্যাট্রিক্স সমীকরণগুলি এর মতো দেখতে পারে:

AX = B, XA = B, AXB = C,

যেখানে A, B, C ম্যাট্রিক্স দেওয়া আছে, X হল কাঙ্খিত ম্যাট্রিক্স।

ম্যাট্রিক্স সমীকরণগুলি বিপরীত ম্যাট্রিক্স দ্বারা সমীকরণকে গুণ করে সমাধান করা হয়।

উদাহরণস্বরূপ, একটি সমীকরণ থেকে ম্যাট্রিক্স খুঁজে পেতে, আপনাকে এই সমীকরণটিকে বাম দিকে দিয়ে গুণ করতে হবে।

অতএব, সমীকরণের সমাধান খুঁজতে, আপনাকে ইনভার্স ম্যাট্রিক্স খুঁজে বের করতে হবে এবং সমীকরণের ডান পাশের ম্যাট্রিক্স দিয়ে গুণ করতে হবে।

অন্যান্য সমীকরণ একইভাবে সমাধান করা হয়।

উদাহরণ 2

AX = B যদি সমীকরণটি সমাধান করুন

সমাধান: যেহেতু ম্যাট্রিক্সের বিপরীত সমান (উদাহরণ 1 দেখুন)

অর্থনৈতিক বিশ্লেষণে ম্যাট্রিক্স পদ্ধতি

অন্যদের সাথে, তারাও আবেদন খুঁজে পায় ম্যাট্রিক্স পদ্ধতি. এই পদ্ধতিগুলি রৈখিক এবং ভেক্টর-ম্যাট্রিক্স বীজগণিতের উপর ভিত্তি করে। জটিল এবং বহুমাত্রিক অর্থনৈতিক ঘটনা বিশ্লেষণের উদ্দেশ্যে এই ধরনের পদ্ধতি ব্যবহার করা হয়। প্রায়শই, এই পদ্ধতিগুলি ব্যবহার করা হয় যখন সংস্থাগুলির কার্যকারিতা এবং তাদের কাঠামোগত বিভাগগুলির তুলনা করার প্রয়োজন হয়।

বিশ্লেষণের ম্যাট্রিক্স পদ্ধতি প্রয়োগের প্রক্রিয়ায়, বিভিন্ন পর্যায়ে পার্থক্য করা যেতে পারে।

প্রথম পর্যায়েঅর্থনৈতিক সূচকগুলির একটি সিস্টেম গঠন করা হয় এবং এর ভিত্তিতে প্রাথমিক ডেটার একটি ম্যাট্রিক্স সংকলিত হয়, যা একটি টেবিল যেখানে সিস্টেম নম্বরগুলি তার পৃথক লাইনে দেখানো হয় (i = 1,2,....,n), এবং উল্লম্ব গ্রাফ বরাবর - সূচকের সংখ্যা (j = 1,2, ....,m).

দ্বিতীয় পর্যায়েপ্রতিটি উল্লম্ব কলামের জন্য, সূচকগুলির উপলব্ধ মানগুলির মধ্যে বৃহত্তমটি প্রকাশিত হয়, যা একটি ইউনিট হিসাবে নেওয়া হয়।

এর পরে, এই কলামে প্রতিফলিত সমস্ত পরিমাণকে বৃহত্তম মান দ্বারা ভাগ করা হয় এবং প্রমিত সহগগুলির একটি ম্যাট্রিক্স গঠিত হয়।

তৃতীয় পর্যায়েম্যাট্রিক্সের সমস্ত উপাদান বর্গাকার। যদি তাদের আলাদা তাত্পর্য থাকে, তবে ম্যাট্রিক্সের প্রতিটি সূচককে একটি নির্দিষ্ট ওজন সহগ বরাদ্দ করা হয় k. পরেরটির মান একজন বিশেষজ্ঞ দ্বারা নির্ধারিত হয়।

শেষের দিকে চতুর্থ পর্যায়রেটিং এর মান পাওয়া গেছে আরজেবৃদ্ধি বা হ্রাসের ক্রমে গোষ্ঠীবদ্ধ।

উপরের ম্যাট্রিক্স পদ্ধতিগুলি ব্যবহার করা উচিত, উদাহরণস্বরূপ, বিভিন্ন বিনিয়োগ প্রকল্পের তুলনামূলক বিশ্লেষণে, সেইসাথে সংস্থাগুলির অন্যান্য অর্থনৈতিক কর্মক্ষমতা সূচকের মূল্যায়নে।

বিপরীত ম্যাট্রিক্সএকটি ম্যাট্রিক্স হয় ক -1, প্রদত্ত প্রাথমিক ম্যাট্রিক্স যা দিয়ে গুণ করা হয় কপরিচয় ম্যাট্রিক্স দেয় ই:

AA −1 = A −1 A =ই.

ইনভার্স ম্যাট্রিক্স পদ্ধতি।

ইনভার্স ম্যাট্রিক্স পদ্ধতি- এটি ম্যাট্রিক্স সমাধানের জন্য সবচেয়ে সাধারণ পদ্ধতিগুলির মধ্যে একটি এবং রৈখিক বীজগণিত সমীকরণ (SLAE) এর সিস্টেমগুলি সমাধান করতে ব্যবহৃত হয় যেখানে অজানা সংখ্যা সমীকরণের সংখ্যার সাথে মিলে যায়।

একটা ব্যবস্থা থাকুক nসঙ্গে রৈখিক সমীকরণ nঅজানা:

এই ধরনের একটি সিস্টেম একটি ম্যাট্রিক্স সমীকরণ হিসাবে লেখা যেতে পারে A*X=B,

কোথায়
- সিস্টেম ম্যাট্রিক্স,

- অজানা কলাম,

- বিনামূল্যে সহগ কলাম।

প্রাপ্ত ম্যাট্রিক্স সমীকরণ থেকে, আমরা বাম দিকের ম্যাট্রিক্স সমীকরণের উভয় দিক দিয়ে গুণ করে X প্রকাশ করি ক-১, ফলে:

A -1 * A * X = A -1 * B

জানে যে A-1*A=E, তারপর E*X=A-1*Bবা X=A-1*B.

পরবর্তী ধাপ হল বিপরীত ম্যাট্রিক্স নির্ধারণ করা ক-১এবং বিনামূল্যে সদস্যদের কলাম দ্বারা গুণিত খ.

ইনভার্স ম্যাট্রিক্স থেকে ম্যাট্রিক্স কশুধুমাত্র যখন বিদ্যমান det A≠ 0 . এই বিবেচনায়, বিপরীত ম্যাট্রিক্স পদ্ধতিতে SLAE সমাধান করার সময়, প্রথম ধাপটি খুঁজে বের করা det A. যদি একটি det A≠ 0 , তারপর সিস্টেমের শুধুমাত্র একটি সমাধান আছে, যা ইনভার্স ম্যাট্রিক্স পদ্ধতি দ্বারা প্রাপ্ত করা যেতে পারে, যদি det A = 0, তারপর যেমন একটি সিস্টেম ইনভার্স ম্যাট্রিক্স পদ্ধতিসমাধান করা হয় না।

বিপরীত ম্যাট্রিক্স সমাধান।

জন্য কর্মের ক্রম ইনভার্স ম্যাট্রিক্স সমাধান:

1. ম্যাট্রিক্স নির্ধারক পান ক. নির্ধারকটি শূন্যের চেয়ে বড় হলে, আমরা বিপরীত ম্যাট্রিক্সটিকে আরও সমাধান করি, যদি এটি শূন্যের সমান হয়, তবে বিপরীত ম্যাট্রিক্সটি এখানে পাওয়া যাবে না।
2. ট্রান্সপোজড ম্যাট্রিক্স খোঁজা AT.
3. আমরা বীজগণিতের পরিপূরকগুলির সন্ধান করি, তারপরে আমরা ম্যাট্রিক্সের সমস্ত উপাদানকে তাদের বীজগণিতের পরিপূরকগুলির সাথে প্রতিস্থাপন করি।
4. আমরা বীজগণিত সংযোজন থেকে বিপরীত ম্যাট্রিক্স সংগ্রহ করি: আমরা প্রাথমিকভাবে প্রদত্ত ম্যাট্রিক্সের নির্ধারক দ্বারা ফলিত ম্যাট্রিক্সের সমস্ত উপাদানকে ভাগ করি। চূড়ান্ত ম্যাট্রিক্সটি আসলটির সাপেক্ষে কাঙ্ক্ষিত বিপরীত ম্যাট্রিক্স হবে।

নিচের অ্যালগরিদম ইনভার্স ম্যাট্রিক্স সমাধানমূলত উপরের মত একই, পার্থক্য শুধুমাত্র কয়েকটি ধাপে: প্রথমত, আমরা বীজগণিতের সংযোজন নির্ধারণ করি এবং তারপরে আমরা ইউনিয়ন ম্যাট্রিক্স গণনা করি গ.

1. প্রদত্ত ম্যাট্রিক্সটি বর্গ কিনা তা খুঁজে বের করুন। একটি নেতিবাচক উত্তরের ক্ষেত্রে, এটি স্পষ্ট হয়ে যায় যে এটির জন্য একটি বিপরীত ম্যাট্রিক্স থাকতে পারে না।
2. প্রদত্ত ম্যাট্রিক্সটি বর্গ কিনা তা খুঁজে বের করুন। একটি নেতিবাচক উত্তরের ক্ষেত্রে, এটি স্পষ্ট হয়ে যায় যে এটির জন্য একটি বিপরীত ম্যাট্রিক্স থাকতে পারে না।
3. আমরা বীজগাণিতিক সংযোজন গণনা করি।
4. আমরা জোটবদ্ধ (পারস্পরিক, সংযুক্ত) ম্যাট্রিক্স রচনা করি গ.
5. আমরা বীজগাণিতিক সংযোজন থেকে একটি বিপরীত ম্যাট্রিক্স রচনা করি: সংলগ্ন ম্যাট্রিক্সের সমস্ত উপাদান গপ্রাথমিক ম্যাট্রিক্সের নির্ধারক দ্বারা ভাগ করুন। ফলস্বরূপ ম্যাট্রিক্সটি প্রদত্ত একটির সাপেক্ষে কাঙ্ক্ষিত বিপরীত ম্যাট্রিক্স হবে।
6. আমরা কাজটি পরীক্ষা করি: আমরা প্রাথমিক এবং ফলাফলের ম্যাট্রিক্সগুলিকে গুণ করি, ফলাফলটি পরিচয় ম্যাট্রিক্স হওয়া উচিত।

এটি একটি সংযুক্ত ম্যাট্রিক্স দিয়ে করা ভাল।

উপপাদ্য: যদি আমরা ডান দিকের একটি বর্গ ম্যাট্রিক্সে একই ক্রমে একটি আইডেন্টিটি ম্যাট্রিক্স বরাদ্দ করি এবং বাম দিকের প্রারম্ভিক ম্যাট্রিক্সটিকে সারিগুলির উপর প্রাথমিক রূপান্তর ব্যবহার করে একটি ইউনিট ম্যাট্রিক্সে রূপান্তরিত করি, তাহলে ডান দিকে প্রাপ্ত একটিটি বিপরীত হবে প্রাথমিক এক

বিপরীত ম্যাট্রিক্স খোঁজার একটি উদাহরণ।

ব্যায়াম। ম্যাট্রিক্সের জন্য সংলগ্ন ম্যাট্রিক্স পদ্ধতি দ্বারা বিপরীত খুঁজুন.

সমাধান। আমরা প্রদত্ত ম্যাট্রিক্সে যোগ করি কিন্তুডানদিকে, ২য় অর্ডারের আইডেন্টিটি ম্যাট্রিক্স:

১ম লাইন থেকে ২য় বিয়োগ করুন:

দ্বিতীয় লাইন থেকে প্রথম 2 বিয়োগ করুন: