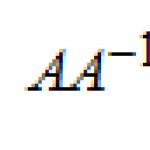লগারিদমের গ্রহণযোগ্য পরিসর (ODZ)
এখন সীমাবদ্ধতা সম্পর্কে কথা বলা যাক (ODZ - ভেরিয়েবলের গ্রহণযোগ্য মানগুলির ক্ষেত্র)।
আমরা মনে করি যে, উদাহরণস্বরূপ, বর্গমূল নেতিবাচক সংখ্যা থেকে নেওয়া যায় না; অথবা যদি আমাদের একটি ভগ্নাংশ থাকে, তাহলে হরটি শূন্যের সমান হতে পারে না। লগারিদমের জন্য অনুরূপ সীমাবদ্ধতা আছে:
অর্থাৎ, যুক্তি এবং ভিত্তি উভয়ই শূন্যের চেয়ে বড় হতে হবে এবং ভিত্তি সমান হতে পারে না।
কেন এমন হল?
চলুন সহজ শুরু করা যাক: আসুন এটি বলি। তারপরে, উদাহরণস্বরূপ, সংখ্যাটি বিদ্যমান নেই, যেহেতু আমরা যে ডিগ্রিই বাড়াই না কেন, এটি সর্বদা দেখা যায়। তদুপরি, এটি কারও জন্য বিদ্যমান নেই। তবে একই সময়ে এটি যে কোনও কিছুর সমান হতে পারে (একই কারণে - এটি যে কোনও ডিগ্রির সমান)। অতএব, বস্তুটি কোন আগ্রহের নয়, এবং এটি কেবল গণিতের বাইরে নিক্ষিপ্ত হয়েছিল।
আমাদের ক্ষেত্রেও একই সমস্যা রয়েছে: যেকোনো ইতিবাচক মাত্রায় - এটি, তবে এটিকে একেবারেই নেতিবাচক শক্তিতে উন্নীত করা যাবে না, যেহেতু শূন্য দ্বারা বিভাজনের ফলাফল হবে (আমি আপনাকে মনে করিয়ে দিচ্ছি)।
যখন আমরা একটি ভগ্নাংশ শক্তিতে উত্থাপনের সমস্যার সম্মুখীন হই (যা একটি মূল হিসাবে উপস্থাপিত হয়:। উদাহরণস্বরূপ, (যে), কিন্তু বিদ্যমান নেই।
অতএব, নেতিবাচক কারণগুলি তাদের সাথে জগাখিচুড়ি করার চেয়ে ফেলে দেওয়া সহজ।
ঠিক আছে, যেহেতু বেস a আমাদের জন্য শুধুমাত্র ইতিবাচক, তাহলে আমরা এটিকে যে ডিগ্রিই বাড়াই না কেন, আমরা সর্বদা একটি কঠোরভাবে ধনাত্মক সংখ্যা পাব। তাই যুক্তি অবশ্যই ইতিবাচক হতে হবে। উদাহরণস্বরূপ, এটি বিদ্যমান নেই, যেহেতু এটি কোনও পরিমাণে একটি ঋণাত্মক সংখ্যা হবে না (এবং এমনকি শূন্য, তাই এটিরও অস্তিত্ব নেই)।
লগারিদমের সমস্যায়, প্রথম ধাপ হল ODZ লিখতে হবে। আমি একটি উদাহরণ দেব:
আসুন সমীকরণটি সমাধান করি।
সংজ্ঞাটি স্মরণ করুন: লগারিদম হল এমন একটি শক্তি যার দিকে একটি যুক্তি পাওয়ার জন্য ভিত্তিটিকে উত্থাপন করতে হবে। এবং শর্ত দ্বারা, এই ডিগ্রী সমান: .
আমরা স্বাভাবিক দ্বিঘাত সমীকরণ পাই: আমরা ভিয়েটা উপপাদ্য ব্যবহার করে এটি সমাধান করি: শিকড়ের যোগফল সমান এবং গুণফল। বাছাই করা সহজ, এই সংখ্যা এবং.
কিন্তু আপনি যদি অবিলম্বে উত্তরে এই দুটি সংখ্যাই নিয়ে যান এবং লিখে দেন, তাহলে আপনি কাজের জন্য 0 পয়েন্ট পেতে পারেন। কেন? আসুন চিন্তা করি যদি আমরা এই মূলগুলিকে প্রাথমিক সমীকরণে প্রতিস্থাপন করি তবে কী হবে?
এটি স্পষ্টতই মিথ্যা, যেহেতু ভিত্তিটি নেতিবাচক হতে পারে না, অর্থাৎ, মূলটি "তৃতীয় পক্ষ"।
এই ধরনের অপ্রীতিকর কৌশলগুলি এড়াতে, আপনি সমীকরণটি সমাধান করা শুরু করার আগেও আপনাকে ODZ লিখতে হবে:
তারপর, শিকড়গুলি পেয়ে এবং, আমরা অবিলম্বে মূলটি বাতিল করে দিই এবং সঠিক উত্তর লিখি।
উদাহরণ 1(নিজেই সমাধান করার চেষ্টা করুন) :
সমীকরণের মূল খুঁজুন। যদি একাধিক শিকড় থাকে তবে আপনার উত্তরে ছোটটি নির্দেশ করুন।
সমাধান:
প্রথমত, ODZ লিখি:
এখন আমরা মনে করি লগারিদম কী: যুক্তি পাওয়ার জন্য আপনাকে কোন শক্তিতে ভিত্তি বাড়াতে হবে? দ্বিতীয়টিতে। এটাই:
মনে হবে যে ছোট রুট সমান। তবে এটি এমন নয়: ওডিজেড অনুসারে, মূলটি তৃতীয় পক্ষ, অর্থাৎ এটি এই সমীকরণের মূল নয়। সুতরাং, সমীকরণের শুধুমাত্র একটি মূল আছে: .
উত্তর: .
মৌলিক লগারিদমিক পরিচয়
সাধারণ পরিভাষায় লগারিদমের সংজ্ঞাটি স্মরণ করুন:
লগারিদমের পরিবর্তে দ্বিতীয় সমতায় প্রতিস্থাপন করুন:
এই সমতা বলা হয় মৌলিক লগারিদমিক পরিচয়. যদিও সারমর্মে এই সমতা শুধু ভিন্নভাবে লেখা হয় লগারিদমের সংজ্ঞা:
এটি পাওয়ার জন্য আপনাকে বাড়াতে হবে এমন শক্তি।
উদাহরণ স্বরূপ:
নিম্নলিখিত উদাহরণগুলি সমাধান করুন:
উদাহরণ 2
অভিব্যক্তির মান নির্ণয় কর।
সমাধান:
বিভাগ থেকে নিয়মটি স্মরণ করুন:, অর্থাৎ, যখন একটি শক্তিকে একটি ডিগ্রি বাড়ানো হয়, তখন সূচকগুলি গুণিত হয়। আসুন এটি প্রয়োগ করা যাক:
উদাহরণ 3
প্রমাণ কর যে.
সমাধান:
লগারিদমের বৈশিষ্ট্য
দুর্ভাগ্যক্রমে, কাজগুলি সর্বদা এত সহজ হয় না - প্রায়শই আপনাকে প্রথমে অভিব্যক্তিটি সরল করতে হবে, এটিকে স্বাভাবিক আকারে আনতে হবে এবং শুধুমাত্র তখনই মান গণনা করা সম্ভব হবে। এটা জেনে এটা করা সবচেয়ে সহজ লগারিদমের বৈশিষ্ট্য. তাহলে আসুন লগারিদমের মৌলিক বৈশিষ্ট্যগুলি শিখি। আমি তাদের প্রত্যেককে প্রমাণ করব, কারণ যে কোনও নিয়ম মনে রাখা সহজ যদি আপনি জানেন যে এটি কোথা থেকে এসেছে।
এই সমস্ত বৈশিষ্ট্যগুলি অবশ্যই মনে রাখতে হবে; এগুলি ছাড়া লগারিদমের বেশিরভাগ সমস্যার সমাধান করা যায় না।
এবং এখন লগারিদমের সমস্ত বৈশিষ্ট্য সম্পর্কে আরও বিশদে।
সম্পত্তি 1:
প্রমাণ:
যাক, তাহলে.
আমাদের আছে: , h.t.d.
বৈশিষ্ট্য 2: লগারিদমের সমষ্টি
একই বেস সহ লগারিদমের যোগফল গুণফলের লগারিদমের সমান: .
প্রমাণ:
যাক, তাহলে. যাক, তাহলে.
উদাহরণ:অভিব্যক্তির মান খুঁজুন:
সমাধান:।
আপনি এইমাত্র যে সূত্রটি শিখেছেন তা লগারিদমগুলির যোগফলকে সহজ করতে সাহায্য করে, পার্থক্য নয়, তাই এই লগারিদমগুলি এখনই একত্রিত করা যাবে না। কিন্তু আপনি বিপরীতটি করতে পারেন - প্রথম লগারিদমটিকে দুটি ভাগে "ব্রেক" করুন: এবং এখানে প্রতিশ্রুত সরলীকরণটি রয়েছে:
.
কেন এই প্রয়োজন? ভাল, উদাহরণস্বরূপ: এটা কি ব্যাপার?
এখন এটা স্পষ্ট যে.
এখন নিজের জন্য এটি সহজ করুন:
কাজ:
উত্তর:
বৈশিষ্ট্য 3: লগারিদমের পার্থক্য:
প্রমাণ:
অনুচ্ছেদ 2 এর মতো সবকিছুই ঠিক একই রকম:
যাক, তাহলে.
যাক, তাহলে. আমাদের আছে:
শেষ বিন্দু থেকে উদাহরণ এখন আরও সহজ:
আরও জটিল উদাহরণ: . নিজেকে অনুমান কিভাবে সিদ্ধান্ত?
এখানে এটি লক্ষ করা উচিত যে লগারিদম বর্গ সম্পর্কে আমাদের একটি একক সূত্র নেই। এটি একটি অভিব্যক্তির অনুরূপ কিছু - এটি এখনই সরলীকৃত করা যাবে না।
অতএব, আসুন লগারিদম সম্পর্কে সূত্রগুলি থেকে সরে আসা যাক এবং চিন্তা করি আমরা সাধারণত গণিতে কোন সূত্রগুলি ব্যবহার করি? 7ম শ্রেণী থেকে!
এটা -. আপনাকে অভ্যস্ত করতে হবে যে তারা সর্বত্র রয়েছে! এবং সূচকীয়, এবং ত্রিকোণমিতিক এবং অযৌক্তিক সমস্যাগুলিতে, তারা পাওয়া যায়। অতএব, তাদের অবশ্যই মনে রাখতে হবে।
আপনি যদি প্রথম দুটি পদ ঘনিষ্ঠভাবে তাকান তবে এটি স্পষ্ট হয়ে যায় যে এটি বর্গক্ষেত্রের পার্থক্য:
চেক করার উত্তর:
নিজেকে সরল করুন।
উদাহরণ
উত্তর।
বৈশিষ্ট্য 4: লগারিদমের যুক্তি থেকে সূচকের উৎপত্তি:
প্রমাণ:এবং এখানে আমরা লগারিদমের সংজ্ঞাটিও ব্যবহার করি: যাক, তারপর। আমাদের আছে: , h.t.d.
আপনি এই নিয়মটি এভাবে বুঝতে পারেন:
অর্থাৎ, যুক্তির ডিগ্রিকে লগারিদমের সামনে নিয়ে যাওয়া হয়, একটি সহগ হিসাবে।
উদাহরণ:অভিব্যক্তির মান নির্ণয় কর।
সমাধান: .
নিজের জন্য সিদ্ধান্ত নিন:
উদাহরণ:
উত্তর:
বৈশিষ্ট্য 5: লগারিদমের ভিত্তি থেকে সূচকের উৎপত্তি:
প্রমাণ:যাক, তাহলে.
আমাদের আছে: , h.t.d.
মনে রাখবেন: থেকে ভিত্তিডিগ্রী হিসাবে রেন্ডার করা হয় বিপরীতসংখ্যা, আগের ক্ষেত্রে ভিন্ন!
বৈশিষ্ট্য 6: বেস থেকে সূচকের উৎপত্তি এবং লগারিদমের যুক্তি:
অথবা যদি ডিগ্রী একই হয়: .
সম্পত্তি 7: নতুন বেসে স্থানান্তর:
প্রমাণ:যাক, তাহলে.
আমাদের আছে: , h.t.d.
বৈশিষ্ট্য 8: লগারিদমের ভিত্তি এবং যুক্তি অদলবদল করা:
প্রমাণ:এটি সূত্র 7 এর একটি বিশেষ কেস: যদি আমরা প্রতিস্থাপন করি, আমরা পাই: , p.t.d.
আসুন আরও কয়েকটি উদাহরণ দেখি।
উদাহরণ 4
অভিব্যক্তির মান নির্ণয় কর।
আমরা লগারিদম নং 2 এর বৈশিষ্ট্য ব্যবহার করি - একই বেস সহ লগারিদমের যোগফল গুণফলের লগারিদমের সমান:
উদাহরণ 5
অভিব্যক্তির মান নির্ণয় কর।
সমাধান:
আমরা লগারিদম নং 3 এবং নং 4 এর বৈশিষ্ট্য ব্যবহার করি:
উদাহরণ 6
অভিব্যক্তির মান নির্ণয় কর।
সমাধান:
সম্পত্তি নম্বর 7 ব্যবহার করে - বেস 2 এ যান:
উদাহরণ 7
অভিব্যক্তির মান নির্ণয় কর।
সমাধান:
আপনি নিবন্ধটি কিভাবে পছন্দ করেন?
আপনি যদি এই লাইনগুলি পড়ছেন, তাহলে আপনি সম্পূর্ণ নিবন্ধটি পড়েছেন।
এবং এটা শান্ত!
এখন বলুন আপনার লেখাটি কেমন লেগেছে?
আপনি লগারিদম সমাধান করতে শিখেছি? না হলে সমস্যা কি?
নীচের মন্তব্যে আমাদের লিখুন.
এবং হ্যাঁ, আপনার পরীক্ষার জন্য শুভকামনা।
ইউনিফাইড স্টেট পরীক্ষা এবং OGE এবং সাধারণভাবে জীবনে
লগারিদম সঠিক নাম্বারভিত্তি থেকে N(খ> 0, খ 1 ) সূচক বলা হয়এক্স , যা আপনাকে বাড়াতে হবেখ N পেতে .
লগারিদম স্বরলিপি:
এই এন্ট্রিটি নিম্নলিখিতগুলির সমতুল্য:b x = N .
উদাহরণ: লগ 3 81 \u003d 4, থেকে 3 4 \u003d 81;
লগ 1/3 27 = – 3 , যেহেতু (1/3) - 3 = 3 3 = 27।
লগারিদমের উপরের সংজ্ঞাটি একটি পরিচয় হিসাবে লেখা যেতে পারে:
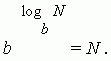
লগারিদমের মৌলিক বৈশিষ্ট্য।
1) লগ খ= 1 , কারণ খ 1 = খ.
খ
2) লগ 1 = 0 , কারণ খ 0 = 1 .
খ
3) পণ্যের লগারিদম গুণনীয়কগুলির লগারিদমের যোগফলের সমান:
লগ( ab) = লগ ক+লগ খ.
4) ভাগফলের লগারিদম লভ্যাংশ এবং ভাজকের লগারিদমের মধ্যে পার্থক্যের সমান:
লগ( ক/খ) = লগ ক-লগ খ.
5) ডিগ্রির লগারিদম সূচকের গুণফল এবং তার ভিত্তির লগারিদমের সমান:
লগ (খ k ) = kলগ খ.
এই সম্পত্তির ফলাফল নিম্নরূপ:লগ রুট মূল সংখ্যার লগারিদমকে মূলের শক্তি দ্বারা ভাগ করে সমান করে:

6) লগারিদমের ভিত্তি যদি একটি ডিগ্রি হয়, তাহলে মান লগের চিহ্ন থেকে এক্সপোনেন্টের পারস্পরিক চিহ্ন বের করা যেতে পারেছড়া:

শেষ দুটি বৈশিষ্ট্য একটিতে একত্রিত করা যেতে পারে:

7) ট্রানজিশন মডুলাস সূত্র (যেমন। e . একটি ভিত্তি থেকে রূপান্তরলগারিদম অন্য বেসে):

একটি বিশেষ ক্ষেত্রে, যখন N=aআমাদের আছে:

দশমিক লগারিদম ডাকা বেস লগারিদম 10. এটা মনোনীত করা হয় lg, অর্থাৎ লগ 10 এন = এলজি এন. 10, 100, 1000, ... সংখ্যার লগারিদমপি যথাক্রমে 1, 2, 3, …,সেগুলো. অনেক ইতিবাচক আছে
একক, লগারিদম সংখ্যায় একের পর কতটি শূন্য রয়েছে। সংখ্যার লগারিদম 0.1, 0.01, 0.001, ...পি avny যথাক্রমে -1, –2, -3, …, i.e. লগারিদম সংখ্যায় একটির আগে যত শূন্য আছে তত নেতিবাচক আছে ( গণনা এবং শূন্য পূর্ণসংখ্যা) লগারিদম অন্যান্য সংখ্যার একটি ভগ্নাংশ বলা হয় ম্যান্টিসা. পুরোলগারিদমের অংশ বলা হয় বৈশিষ্ট্য. ব্যবহারিক জন্যদশমিক লগারিদম সবচেয়ে সুবিধাজনক।
প্রাকৃতিক লগারিদম
ডাকা বেস লগারিদম
e. এটি চিহ্নিত করা হয় ln, অর্থাৎ লগ eএন
=
ln এন. সংখ্যা eঅযৌক্তিক,আনুমানিক মান হল 2.718281828।এটা সংখ্যাটি যে সীমার দিকে ঝোঁক(1 + 1
/
n)
n সীমাহীন বৃদ্ধি সহn(সেমি. প্রথম বিস্ময়কর সীমা ).
এটি অদ্ভুত বলে মনে হতে পারে, প্রাকৃতিক লগারিদমগুলি ফাংশনগুলির বিশ্লেষণ সম্পর্কিত বিভিন্ন ক্রিয়াকলাপ পরিচালনা করার সময় খুব সুবিধাজনক বলে প্রমাণিত হয়েছিল।বেস লগারিদম গণনা করা হচ্ছেeঅন্য কোন ভিত্তির তুলনায় অনেক দ্রুত।
সুতরাং, আমাদের দুটি ক্ষমতা আছে। আপনি যদি নীচের লাইন থেকে নম্বরটি নেন, তাহলে আপনি সহজেই খুঁজে পেতে পারেন যে এই নম্বরটি পেতে আপনাকে একটি দুটি বাড়াতে হবে। উদাহরণস্বরূপ, 16 পেতে, আপনাকে দুই থেকে চতুর্থ শক্তি বাড়াতে হবে। এবং 64 পেতে, আপনাকে দুই থেকে ষষ্ঠ শক্তি বাড়াতে হবে। এটি টেবিল থেকে দেখা যায়।
এবং এখন - আসলে, লগারিদমের সংজ্ঞা:
আর্গুমেন্ট x-এর বেস a লগারিদম হল সেই শক্তি যার দিকে x সংখ্যা পেতে হলে a সংখ্যাটিকে অবশ্যই বাড়াতে হবে।
নোটেশন: লগ a x \u003d b, যেখানে a হল বেস, x হল আর্গুমেন্ট, b আসলে লগারিদমের সমান।
উদাহরণস্বরূপ, 2 3 = 8 ⇒ লগ 2 8 = 3 (8 এর ভিত্তি 2 লগারিদম তিনটি কারণ 2 3 = 8)। পাশাপাশি 2 64 = 6 লগ হতে পারে, যেহেতু 2 6 = 64।
একটি প্রদত্ত বেস থেকে একটি সংখ্যার লগারিদম খুঁজে বের করার অপারেশনকে লগারিদম বলে। সুতরাং আসুন আমাদের টেবিলে একটি নতুন সারি যোগ করি:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| লগ 2 2 = 1 | লগ 2 4 = 2 | লগ 2 8 = 3 | লগ 2 16 = 4 | লগ 2 32 = 5 | লগ 2 64 = 6 |
দুর্ভাগ্যবশত, সমস্ত লগারিদম এত সহজে বিবেচনা করা হয় না। উদাহরণস্বরূপ, লগ 2 5 খুঁজে বের করার চেষ্টা করুন। 5 নম্বরটি টেবিলে নেই, তবে যুক্তি নির্দেশ করে যে লগারিদমটি সেগমেন্টের কোথাও থাকবে। কারণ 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
এই ধরনের সংখ্যাগুলিকে অযৌক্তিক বলা হয়: দশমিক বিন্দুর পরে সংখ্যাগুলি অনির্দিষ্টকালের জন্য লেখা যেতে পারে এবং সেগুলি কখনই পুনরাবৃত্তি হয় না। লগারিদম যদি অযৌক্তিক হয়ে ওঠে, তাহলে এটিকে এভাবে ছেড়ে দেওয়া ভাল: লগ 2 5, লগ 3 8, লগ 5 100৷
এটা বোঝা গুরুত্বপূর্ণ যে লগারিদম দুটি ভেরিয়েবল (বেস এবং আর্গুমেন্ট) সহ একটি অভিব্যক্তি। প্রথমে, অনেকে বিভ্রান্ত করে যে ভিত্তি কোথায় এবং যুক্তি কোথায়। বিরক্তিকর ভুল বোঝাবুঝি এড়াতে, শুধু ছবিটি দেখুন:
আমাদের সামনে লগারিদমের সংজ্ঞা ছাড়া আর কিছুই নয়। মনে রাখবেন: লগারিদম হল শক্তি, যা আপনাকে যুক্তি পেতে ভিত্তি বাড়াতে হবে। এটি বেস যা একটি শক্তিতে উত্থাপিত হয় - ছবিতে এটি লাল রঙে হাইলাইট করা হয়েছে। দেখা যাচ্ছে যে বেস সবসময় নীচে থাকে! আমি প্রথম পাঠেই আমার ছাত্রদের এই বিস্ময়কর নিয়মটি বলি - এবং কোন বিভ্রান্তি নেই।
আমরা সংজ্ঞাটি বের করেছি - লগারিদমগুলি কীভাবে গণনা করা যায় তা শিখতে বাকি আছে, যেমন "লগ" চিহ্ন থেকে মুক্তি পান। শুরুতে, আমরা লক্ষ্য করি যে দুটি গুরুত্বপূর্ণ তথ্য সংজ্ঞা থেকে অনুসরণ করে:
- যুক্তি এবং ভিত্তি সর্বদা শূন্যের চেয়ে বড় হতে হবে। এটি একটি যৌক্তিক সূচক দ্বারা ডিগ্রির সংজ্ঞা থেকে অনুসরণ করে, যেখানে লগারিদমের সংজ্ঞা হ্রাস করা হয়।
- ভিত্তিটি অবশ্যই ঐক্য থেকে আলাদা হতে হবে, যেহেতু একটি ইউনিট থেকে যেকোনো শক্তি এখনও একটি ইউনিট। এই কারণে, "দুটি পাওয়ার জন্য একজনকে কোন শক্তিতে উত্থাপন করতে হবে" এই প্রশ্নটি অর্থহীন। এমন কোন ডিগ্রি নেই!
এই ধরনের নিষেধাজ্ঞা বলা হয় বৈধ পরিসীমা(ODZ)। দেখা যাচ্ছে যে লগারিদমের ODZ দেখতে এইরকম: লগ a x = b ⇒ x > 0, a > 0, a ≠ 1।
উল্লেখ্য যে সংখ্যা b এর উপর কোন সীমাবদ্ধতা নেই (লগারিদমের মান) আরোপ করা হয়নি। উদাহরণস্বরূপ, লগারিদমটি নেতিবাচক হতে পারে: লগ 2 0.5 = −1, কারণ 0.5 = 2 −1।
যাইহোক, এখন আমরা শুধুমাত্র সংখ্যাসূচক রাশি বিবেচনা করছি, যেখানে লগারিদমের ODZ জানার প্রয়োজন নেই। সমস্ত বিধিনিষেধ ইতিমধ্যেই সমস্যাগুলির সংকলক দ্বারা বিবেচনা করা হয়েছে। কিন্তু লগারিদমিক সমীকরণ এবং অসমতা কার্যকর হলে, DHS প্রয়োজনীয়তা বাধ্যতামূলক হয়ে যাবে। প্রকৃতপক্ষে, ভিত্তি এবং যুক্তিতে খুব শক্তিশালী নির্মাণ থাকতে পারে, যা অগত্যা উপরের বিধিনিষেধের সাথে সামঞ্জস্যপূর্ণ নয়।
এখন লগারিদম গণনার জন্য সাধারণ স্কিম বিবেচনা করুন। এটি তিনটি ধাপ নিয়ে গঠিত:
- বেস a এবং আর্গুমেন্ট x কে একটি পাওয়ার হিসাবে প্রকাশ করুন যার সাথে একটির চেয়ে ছোট সম্ভাব্য বেস রয়েছে। পথ বরাবর, এটি দশমিক ভগ্নাংশ পরিত্রাণ পেতে ভাল;
- পরিবর্তনশীল b এর সমীকরণটি সমাধান করুন: x = a b;
- ফলিত সংখ্যা b হবে উত্তর।
এখানেই শেষ! লগারিদম অযৌক্তিক হতে দেখা গেলে, এটি ইতিমধ্যেই প্রথম ধাপে দেখা যাবে। ভিত্তিটি একের চেয়ে বড় হওয়ার প্রয়োজনীয়তা খুবই প্রাসঙ্গিক: এটি ত্রুটির সম্ভাবনা হ্রাস করে এবং গণনাগুলিকে ব্যাপকভাবে সরল করে। একইভাবে দশমিক ভগ্নাংশের সাথে: আপনি যদি অবিলম্বে সেগুলিকে সাধারণগুলিতে রূপান্তর করেন তবে অনেক গুণ কম ত্রুটি হবে।
আসুন দেখি কিভাবে এই স্কিমটি নির্দিষ্ট উদাহরণের সাথে কাজ করে:
একটি কাজ. লগারিদম গণনা করুন: লগ 5 25
- বেস এবং আর্গুমেন্টকে পাঁচটির শক্তি হিসাবে উপস্থাপন করা যাক: 5 = 5 1 ; 25 = 52;
- আসুন সমীকরণটি তৈরি করি এবং সমাধান করি:
লগ 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - একটি উত্তর প্রাপ্ত হয়েছে: 2.
একটি কাজ. লগারিদম গণনা করুন:
একটি কাজ. লগারিদম গণনা করুন: লগ 4 64
- বেস এবং আর্গুমেন্টকে দুইটির শক্তি হিসাবে উপস্থাপন করা যাক: 4 = 2 2 ; 64 = 26;
- আসুন সমীকরণটি তৈরি করি এবং সমাধান করি:
লগ 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3; - একটি উত্তর প্রাপ্ত হয়েছে: 3.
একটি কাজ. লগারিদম গণনা করুন: লগ 16 1
- বেস এবং আর্গুমেন্টকে দুইটির শক্তি হিসাবে উপস্থাপন করা যাক: 16 = 2 4 ; 1 = 20;
- আসুন সমীকরণটি তৈরি করি এবং সমাধান করি:
লগ 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0; - একটি প্রতিক্রিয়া প্রাপ্ত হয়েছে: 0.
একটি কাজ. লগারিদম গণনা করুন: লগ 7 14
- বেস এবং আর্গুমেন্টকে সাতটির শক্তি হিসাবে উপস্থাপন করা যাক: 7 = 7 1 ; 14 সাতটির শক্তি হিসাবে উপস্থাপন করা হয় না, কারণ 7 1< 14 < 7 2 ;
- এটি পূর্ববর্তী অনুচ্ছেদ থেকে অনুসরণ করে যে লগারিদম বিবেচনা করা হয় না;
- উত্তরটি কোন পরিবর্তন নয়: লগ 7 14।
শেষ উদাহরণ একটি ছোট নোট. কিভাবে নিশ্চিত করবেন যে একটি সংখ্যা অন্য সংখ্যার একটি সঠিক শক্তি নয়? খুব সহজ - এটিকে প্রধান কারণগুলিতে পচিয়ে দিন। এবং যদি এই জাতীয় কারণগুলি একই সূচকগুলির সাথে একটি ডিগ্রিতে সংগ্রহ করা না যায়, তবে আসল সংখ্যাটি সঠিক ডিগ্রি নয়।
একটি কাজ. সংখ্যাটির সঠিক ক্ষমতাগুলি কিনা তা খুঁজে বের করুন: 8; 48; 81; 35; চৌদ্দ
8 \u003d 2 2 2 \u003d 2 3 সঠিক ডিগ্রী, কারণ শুধুমাত্র একটি গুণক আছে;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 একটি সঠিক শক্তি নয় কারণ দুটি কারণ রয়েছে: 3 এবং 2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - সঠিক ডিগ্রী;
35 \u003d 7 5 - আবার একটি সঠিক ডিগ্রী নয়;
14 \u003d 7 2 - আবার একটি সঠিক ডিগ্রী নয়;
আরও লক্ষ্য করুন যে মৌলিক সংখ্যাগুলি নিজেরাই সর্বদা নিজের সঠিক শক্তি।
দশমিক লগারিদম
কিছু লগারিদম এত সাধারণ যে তাদের একটি বিশেষ নাম এবং পদবী রয়েছে।
x আর্গুমেন্টের দশমিক লগারিদম হল বেস 10 লগারিদম, অর্থাৎ x সংখ্যা পাওয়ার জন্য আপনাকে যে শক্তিতে 10 নম্বর বাড়াতে হবে। পদবী: lg x।
উদাহরণস্বরূপ, লগ 10 = 1; লগ 100 = 2; lg 1000 = 3 - ইত্যাদি।
এখন থেকে, যখন পাঠ্যপুস্তকে “Find lg 0.01”-এর মতো একটি বাক্যাংশ আসবে, তখন জেনে রাখুন যে এটি কোনো টাইপো নয়। এটি দশমিক লগারিদম। যাইহোক, আপনি যদি এই জাতীয় পদবীতে অভ্যস্ত না হন তবে আপনি সর্বদা এটি পুনরায় লিখতে পারেন:
log x = লগ 10 x
সাধারণ লগারিদমের জন্য যা সত্য তা দশমিকের জন্যও সত্য।
প্রাকৃতিক লগারিদম
আরেকটি লগারিদম আছে যার নিজস্ব স্বরলিপি রয়েছে। এক অর্থে, এটি দশমিকের চেয়েও বেশি গুরুত্বপূর্ণ। এটি প্রাকৃতিক লগারিদম।
আর্গুমেন্ট x এর স্বাভাবিক লগারিদম হল বেস e এর লগারিদম, অর্থাৎ x সংখ্যা পাওয়ার জন্য যে শক্তিতে সংখ্যা e বাড়াতে হবে। পদবী: ln x।
অনেকেই প্রশ্ন করবেঃ ই সংখ্যা আর কি? এটি একটি অমূলদ সংখ্যা, এর সঠিক মান খুঁজে পাওয়া যাবে না এবং লেখা যাবে না। এখানে শুধুমাত্র প্রথম সংখ্যা আছে:
e = 2.718281828459...
এই সংখ্যাটি কী এবং কেন এটি প্রয়োজন তা আমরা অনুসন্ধান করব না। শুধু মনে রাখবেন যে e হল প্রাকৃতিক লগারিদমের ভিত্তি:
ln x = লগ ই x
এইভাবে ln e = 1; লগ ই 2 = 2; ln e 16 = 16 - ইত্যাদি। অন্যদিকে, ln 2 একটি অমূলদ সংখ্যা। সাধারণভাবে, যেকোনো মূলদ সংখ্যার প্রাকৃতিক লগারিদম অমূলদ। ব্যতীত, অবশ্যই, ঐক্য: ln 1 = 0।
প্রাকৃতিক লগারিদমের জন্য, সাধারণ লগারিদমের জন্য সত্য সব নিয়ম বৈধ।
প্রাকৃতিক লগারিদমের প্রধান বৈশিষ্ট্য, গ্রাফ, সংজ্ঞার ডোমেইন, মানের সেট, মৌলিক সূত্র, ডেরিভেটিভ, ইন্টিগ্রাল, পাওয়ার সিরিজে বিস্তৃতি এবং জটিল সংখ্যার মাধ্যমে ln x ফাংশনের উপস্থাপনা দেওয়া হয়েছে।
বিষয়বস্তুবিপরীত ফাংশন
প্রাকৃতিক লগারিদম জন্য পারস্পরিক হয় প্রদর্শক.
যদি, তাহলে
যদি, তাহলে.
ডেরিভেটিভ ln x
প্রাকৃতিক লগারিদমের ডেরিভেটিভ:
.
মডুলো x এর প্রাকৃতিক লগারিদমের ডেরিভেটিভ:
.
nম ক্রম থেকে ডেরিভেটিভ:
.
সূত্রের ব্যুৎপত্তি >>>
অখণ্ড
অখণ্ড গণনা করা হয় অংশ দ্বারা একীকরণ :
.
তাই,
জটিল সংখ্যার পরিপ্রেক্ষিতে অভিব্যক্তি
একটি জটিল পরিবর্তনশীল z এর একটি ফাংশন বিবেচনা করুন:
.
জটিল চলকটি প্রকাশ করা যাক zমডিউল মাধ্যমে rএবং যুক্তি φ
:
.
লগারিদমের বৈশিষ্ট্য ব্যবহার করে, আমাদের আছে:
.
বা
.
যুক্তি φ স্বতন্ত্রভাবে সংজ্ঞায়িত করা হয় না। যদি আমরা রাখি
, যেখানে n একটি পূর্ণসংখ্যা,
তাহলে এটি ভিন্ন n এর জন্য একই সংখ্যা হবে।
অতএব, প্রাকৃতিক লগারিদম, একটি জটিল চলকের একটি ফাংশন হিসাবে, একটি একক-মূল্যবান ফাংশন নয়।
পাওয়ার সিরিজ সম্প্রসারণ
জন্য, সম্প্রসারণ ঘটে:
তথ্যসূত্র:
ভিতরে. ব্রনস্টেইন, কে.এ. সেমেনদিয়েভ, উচ্চতর শিক্ষা প্রতিষ্ঠানের ইঞ্জিনিয়ার এবং শিক্ষার্থীদের জন্য গণিতের হ্যান্ডবুক, ল্যান, 2009।