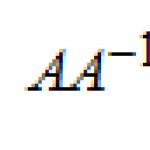সূচকীয় সমীকরণের সমাধান। উদাহরণ।
মনোযোগ!
অতিরিক্ত আছে
বিশেষ ধারা 555 এর উপাদান।
যারা দৃঢ়ভাবে "খুব নয়..." তাদের জন্য
এবং যারা "খুব বেশি ..." তাদের জন্য)
কি সূচকীয় সমীকরণ? এটি একটি সমীকরণ যেখানে অজানা (x) এবং তাদের সাথে অভিব্যক্তি রয়েছে সূচককিছু ডিগ্রী এবং শুধুমাত্র সেখানে! এটা গুরুত্বপূর্ণ.
তুমি এখানে সূচকীয় সমীকরণের উদাহরণ:
3 x 2 x = 8 x + 3
বিঃদ্রঃ! ডিগ্রির বেসে (নীচে) - শুধুমাত্র সংখ্যা. AT সূচকডিগ্রী (উপরে) - এক্স সহ বিভিন্ন ধরনের এক্সপ্রেশন। যদি, হঠাৎ, একটি x সূচক ছাড়া অন্য কোথাও সমীকরণে উপস্থিত হয়, উদাহরণস্বরূপ:
এটি একটি মিশ্র ধরনের সমীকরণ হবে। এই জাতীয় সমীকরণগুলির সমাধানের জন্য স্পষ্ট নিয়ম নেই। আমরা আপাতত তাদের বিবেচনা করব না। এখানে আমরা মোকাবেলা করা হবে সূচকীয় সমীকরণের সমাধানতার বিশুদ্ধতম আকারে।
প্রকৃতপক্ষে, এমনকি বিশুদ্ধ সূচকীয় সমীকরণ সবসময় পরিষ্কারভাবে সমাধান করা হয় না। কিন্তু কিছু নির্দিষ্ট ধরণের সূচকীয় সমীকরণ রয়েছে যেগুলি সমাধান করা যেতে পারে এবং করা উচিত। এই ধরনের আমরা খুঁজছেন হবে.
সহজতম সূচকীয় সমীকরণের সমাধান।
খুব মৌলিক কিছু দিয়ে শুরু করা যাক। উদাহরণ স্বরূপ:
এমনকি কোনো তত্ত্ব ছাড়াই, সাধারণ নির্বাচনের মাধ্যমে এটা স্পষ্ট যে x = 2। আর কিছু না, তাই না!? অন্য কোন x মান রোল নেই। এবং এখন এই জটিল সূচকীয় সমীকরণের সমাধানটি দেখি:
আমরা কি করলাম? আমরা, আসলে, একই বটমগুলি (ট্রিপল) ছুঁড়ে ফেলেছি। পুরোপুরি ছিটকে গেছে। এবং, কি খুশি, চিহ্ন আঘাত!
প্রকৃতপক্ষে, যদি সূচকীয় সমীকরণে বাম এবং ডানদিকে থাকে একইযেকোনো ডিগ্রীতে সংখ্যা, এই সংখ্যাগুলি সরানো যেতে পারে এবং সমান সূচকগুলি। গণিত অনুমতি দেয়। এটি একটি অনেক সহজ সমীকরণ সমাধান করা অবশেষ. এটা ভাল, তাই না?)
যাইহোক, আসুন হাস্যকরভাবে মনে রাখা যাক: আপনি কেবল তখনই ঘাঁটিগুলি সরাতে পারবেন যখন বাম এবং ডান দিকের ভিত্তি সংখ্যাগুলি দুর্দান্ত বিচ্ছিন্নতায় থাকবে!কোন প্রতিবেশী এবং সহগ ছাড়া. আসুন সমীকরণে বলি:
2 x +2 x + 1 = 2 3 , বা
আপনি ডাবল অপসারণ করতে পারবেন না!
ওয়েল, আমরা সবচেয়ে গুরুত্বপূর্ণ জিনিস আয়ত্ত করেছি. কিভাবে খারাপ সূচকীয় অভিব্যক্তি থেকে সরল সমীকরণে সরানো যায়।
"এই যে সময় আছে!" - তুমি বলো. "নিয়ন্ত্রণ ও পরীক্ষায় এমন আদিম কে দেবে!?"
রাজি হতে বাধ্য। কেউ করবে না। কিন্তু এখন আপনি জানেন যে বিভ্রান্তিকর উদাহরণগুলি সমাধান করার সময় কোথায় যেতে হবে। এটা মাথায় আনতে হবে, যখন একই ভিত্তি নম্বর বাম-ডানে থাকে। তারপর সবকিছু সহজ হবে। আসলে, এটি গণিতের ক্লাসিক। আমরা মূল উদাহরণ গ্রহণ এবং পছন্দসই এটি রূপান্তর আমাদেরমন অবশ্যই গণিতের নিয়ম অনুযায়ী।
উদাহরণগুলি বিবেচনা করুন যেগুলিকে সহজে আনতে কিছু অতিরিক্ত প্রচেষ্টার প্রয়োজন। তাদের কল করা যাক সহজ সূচকীয় সমীকরণ।
সরল সূচকীয় সমীকরণের সমাধান। উদাহরণ।
সূচকীয় সমীকরণগুলি সমাধান করার সময়, প্রধান নিয়মগুলি হল ক্ষমতা সহ কর্ম।এই কর্ম সম্পর্কে জ্ঞান ছাড়া, কিছুই কাজ করবে না.
ডিগ্রী সহ কর্মের জন্য, একজনকে অবশ্যই ব্যক্তিগত পর্যবেক্ষণ এবং চতুরতা যোগ করতে হবে। আমরা কি একই ভিত্তি সংখ্যা প্রয়োজন? সুতরাং আমরা একটি স্পষ্ট বা এনক্রিপ্ট করা ফর্ম উদাহরণে তাদের খুঁজছি.
চলুন দেখা যাক কিভাবে এটা করা হয় বাস্তবে?
আমাদের একটি উদাহরণ দেওয়া যাক:
2 2x - 8 x+1 = 0
প্রথম নজরে ভিত্তিতারা... তারা আলাদা! দুই এবং আট. কিন্তু নিরুৎসাহিত করা খুব তাড়াতাড়ি। এটা মনে করার সময়
ডিগ্রীতে দুই এবং আটজন আপেক্ষিক।) এটি লিখে রাখা বেশ সম্ভব:
8 x+1 = (2 3) x+1
যদি আমরা ক্ষমতা সহ ক্রিয়াগুলি থেকে সূত্রটি স্মরণ করি:
(a n) m = a nm ,
এটি সাধারণত দুর্দান্ত কাজ করে:
8 x+1 = (2 3) x+1 = 2 3(x+1)
মূল উদাহরণ এই মত দেখায়:
2 2x - 2 3(x+1) = 0
আমরা স্থানান্তর করি 2 3 (x+1)ডানদিকে (কেউ গণিতের প্রাথমিক ক্রিয়াগুলি বাতিল করেনি!), আমরা পাই:
2 2x \u003d 2 3 (x + 1)
যে কার্যত সব. ঘাঁটি অপসারণ:
আমরা এই দৈত্য সমাধান এবং পেতে
এটা সঠিক উত্তর.
এই উদাহরণে, দুজনের ক্ষমতা জানা আমাদের সাহায্য করেছে। আমরা চিহ্নিতআটটিতে, এনক্রিপ্ট করা ডিউস। এই কৌশলটি (বিভিন্ন সংখ্যার অধীনে সাধারণ বেস এনকোডিং) সূচকীয় সমীকরণে একটি খুব জনপ্রিয় কৌশল! হ্যাঁ, লগারিদমেও। একজনকে অবশ্যই সংখ্যায় অন্যান্য সংখ্যার শক্তি চিনতে সক্ষম হতে হবে। সূচকীয় সমীকরণ সমাধানের জন্য এটি অত্যন্ত গুরুত্বপূর্ণ।
আসল বিষয়টি হ'ল যে কোনও শক্তিতে কোনও সংখ্যা বাড়ানো কোনও সমস্যা নয়। গুন করুন, এমনকি কাগজের টুকরোতে, এবং এটিই সব। উদাহরণস্বরূপ, সবাই 3 থেকে পঞ্চম শক্তি বাড়াতে পারে। যদি আপনি গুণের সারণীটি জানেন তবে 243 বের হবে।) তবে সূচকীয় সমীকরণে, অনেক বেশি প্রায়শই একটি শক্তি বাড়ানোর প্রয়োজন হয় না, তবে বিপরীতে ... কি সংখ্যা কি পরিমাণ 243 নম্বরের পিছনে লুকিয়ে থাকে, বা, বলুন, 343... এখানে কোনও ক্যালকুলেটর আপনাকে সাহায্য করবে না।
আপনাকে কিছু সংখ্যার শক্তি দেখতে হবে, হ্যাঁ... আমরা কি অনুশীলন করব?
কোনটি শক্তি এবং কোন সংখ্যাগুলি সংখ্যা তা নির্ধারণ করুন:
2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729, 1024.
উত্তর (একটি জগাখিচুড়ি, অবশ্যই!):
5 4 ; 2 10 ; 7 3 ; 3 5 ; 2 7 ; 10 2 ; 2 6 ; 3 3 ; 2 3 ; 2 1 ; 3 6 ; 2 9 ; 2 8 ; 6 3 ; 5 3 ; 3 4 ; 2 5 ; 4 4 ; 4 2 ; 2 3 ; 9 3 ; 4 5 ; 8 2 ; 4 3 ; 8 3 .
আপনি যদি খুব কাছ থেকে তাকান, আপনি একটি অদ্ভুত তথ্য দেখতে পাবেন। প্রশ্নের চেয়ে আরও উত্তর আছে! ঠিক আছে, এটা ঘটে... উদাহরণস্বরূপ, 2 6, 4 3, 8 2 সবই 64।
ধরা যাক যে আপনি সংখ্যার সাথে পরিচিত হওয়ার তথ্যটি নোট করেছেন।) আমি আপনাকে মনে করিয়ে দিই যে সূচকীয় সমীকরণ সমাধানের জন্য, আমরা আবেদন করি সমগ্রগাণিতিক জ্ঞানের স্টক। নিম্ন-মধ্যবিত্তদের অন্তর্ভুক্ত। আপনি সরাসরি হাই স্কুলে যাননি, তাই না?
উদাহরণ স্বরূপ, সূচকীয় সমীকরণগুলি সমাধান করার সময়, বন্ধনীর বাইরে সাধারণ গুণকটি রাখা অনেক সময় সাহায্য করে (হ্যালো গ্রেড 7!)। আসুন একটি উদাহরণ দেখি:
3 2x+4 -11 9 x = 210
এবং আবার, প্রথম চেহারা - ভিত্তিতে! ডিগ্রির ভিত্তি ভিন্ন... তিন এবং নয়। এবং আমরা তাদের একই হতে চাই. ঠিক আছে, এই ক্ষেত্রে, ইচ্ছাটি বেশ সম্ভব!) কারণ:
9 x = (3 2) x = 3 2x
ডিগ্রী সহ কর্মের জন্য একই নিয়ম অনুসারে:
3 2x+4 = 3 2x 3 4
এটা চমৎকার, আপনি লিখতে পারেন:
3 2x 3 4 - 11 3 2x = 210
আমরা একই কারণে একটি উদাহরণ দিয়েছি। তো, এরপর কি!? থ্রি ছুঁড়ে ফেলা যায় না... ডেড এন্ড?
একেবারেই না. সবচেয়ে সর্বজনীন এবং শক্তিশালী সিদ্ধান্তের নিয়ম মনে রাখা সবগণিত কাজ:
আপনি কি করতে জানেন না, আপনি কি করতে পারেন!
আপনি দেখুন, সবকিছু গঠিত)।
কি আছে এই সূচকীয় সমীকরণে করতে পারাকরতে? হ্যাঁ, বাম পাশ সরাসরি বন্ধনী চেয়েছে! 3 2x এর সাধারণ ফ্যাক্টর স্পষ্টভাবে এটির ইঙ্গিত দেয়। আসুন চেষ্টা করি, এবং তারপর আমরা দেখতে পাব:
3 2x (3 4 - 11) = 210
3 4 - 11 = 81 - 11 = 70
উদাহরণ আরও ভাল হতে থাকে!
আমরা মনে করি যে ঘাঁটিগুলি নির্মূল করার জন্য, আমাদের কোনও সহগ ছাড়াই একটি বিশুদ্ধ ডিগ্রি প্রয়োজন। 70 নম্বর আমাদের বিরক্ত করে। সুতরাং আমরা সমীকরণের উভয় দিককে 70 দ্বারা ভাগ করি, আমরা পাই:
অপ-পা! সবকিছু ঠিকঠাক হয়েছে!
এই চূড়ান্ত উত্তর.
এটা ঘটবে, যাইহোক, যে একই ভিত্তিতে ট্যাক্সি আউট প্রাপ্ত হয়, কিন্তু তাদের পরিসমাপ্তি হয় না. এটি অন্য ধরনের সূচকীয় সমীকরণে ঘটে। আসুন এই ধরনের পেতে.
সূচকীয় সমীকরণ সমাধানে চলকের পরিবর্তন। উদাহরণ।
আসুন সমীকরণটি সমাধান করি:
4 x - 3 2 x +2 = 0
প্রথম - যথারীতি। এর বেস এগিয়ে চলুন. ডিউসের কাছে।
4 x = (2 2) x = 2 2x
আমরা সমীকরণ পাই:
2 2x - 3 2 x +2 = 0
এবং এখানে আমরা স্তব্ধ হবে. আগের কৌশলগুলি কাজ করবে না, আপনি এটি যেভাবেই ঘোরান না কেন। আমাদের আরেকটি শক্তিশালী এবং বহুমুখী উপায়ের অস্ত্রাগার থেকে পেতে হবে। একে বলে পরিবর্তনশীল প্রতিস্থাপন।
পদ্ধতির সারাংশ আশ্চর্যজনকভাবে সহজ। একটি জটিল আইকনের পরিবর্তে (আমাদের ক্ষেত্রে, 2 x), আমরা আরেকটি লিখি, সহজ একটি (উদাহরণস্বরূপ, t)। এই ধরনের একটি আপাতদৃষ্টিতে অর্থহীন প্রতিস্থাপন আশ্চর্যজনক ফলাফলের দিকে পরিচালিত করে!) সবকিছুই পরিষ্কার এবং বোধগম্য হয়ে যায়!
বেশ দেরি
তারপর 2 2x \u003d 2 x2 \u003d (2 x) 2 \u003d t 2
আমরা আমাদের সমীকরণে x এর সমস্ত শক্তিকে t দ্বারা প্রতিস্থাপন করি:
আচ্ছা, এটা ভোর হয়?) দ্বিঘাত সমীকরণ এখনো ভুলে যাননি? আমরা বৈষম্যকারীর মাধ্যমে সমাধান করি, আমরা পাই:
এখানে, মূল জিনিসটি থামানো নয়, যেমনটি ঘটে ... এটি এখনও উত্তর নয়, আমাদের x দরকার, টি নয়। আমরা Xs এ ফিরে যাই, অর্থাৎ একটি প্রতিস্থাপন করা প্রথম টি 1 এর জন্য:
এটাই,
একটি মূল পাওয়া গেছে। আমরা টি 2 থেকে দ্বিতীয়টি খুঁজছি:
উম... বাম 2 x, ডান 1... একটি বাধা? হ্যাঁ, মোটেই না! এটা মনে রাখা যথেষ্ট (ডিগ্রী সহ কর্ম থেকে, হ্যাঁ ...) যে একটি ঐক্য যেকোনোসংখ্যা শূন্য। যে কোন আপনার যা প্রয়োজন, আমরা তা রাখব। আমরা একটি দুই প্রয়োজন. মানে:
এখন এতটুকুই। 2টি শিকড় পেয়েছেন:
এই উত্তর.
এ সূচকীয় সমীকরণ সমাধান করাশেষে, কিছু বিশ্রী অভিব্যক্তি কখনও কখনও প্রাপ্ত হয়। প্রকার:
সাতটি থেকে, একটি সাধারণ ডিগ্রির মাধ্যমে একটি ডিউস কাজ করে না। তারা আত্মীয় নয়... আমি এখানে কিভাবে থাকবো? কেউ বিভ্রান্ত হতে পারে ... কিন্তু যে ব্যক্তি এই সাইটের বিষয় "লগারিদম কি?" , শুধুমাত্র অল্প অল্প করে হাসুন এবং দৃঢ় হাতে একেবারে সঠিক উত্তরটি লিখুন:
পরীক্ষার "বি" টাস্কে এমন কোনও উত্তর থাকতে পারে না। একটি নির্দিষ্ট সংখ্যা প্রয়োজন. কিন্তু কাজ "সি" - সহজে.
এই পাঠটি সবচেয়ে সাধারণ সূচকীয় সমীকরণগুলি সমাধান করার উদাহরণ প্রদান করে। আসুন প্রধানটি হাইলাইট করি।
ব্যবহারিক টিপস:
1. প্রথমত, আমরা তাকাই ভিত্তিডিগ্রী. দেখা যাক সেগুলো করা যায় না একই.এর সক্রিয়ভাবে ব্যবহার করে এটি করার চেষ্টা করা যাক ক্ষমতা সহ কর্ম।ভুলে যাবেন না যে x ছাড়া সংখ্যাগুলিও ডিগ্রিতে পরিণত হতে পারে!
2. আমরা সূচকীয় সমীকরণটি ফর্মে আনার চেষ্টা করি যখন বাম এবং ডান একইযেকোনো মাত্রায় সংখ্যা। আমরা ব্যাবহার করি ক্ষমতা সহ কর্মএবং ফ্যাক্টরাইজেশনসংখ্যায় কী গণনা করা যায় - আমরা গণনা করি।
3. যদি দ্বিতীয় উপদেশটি কাজ না করে, আমরা পরিবর্তনশীল প্রতিস্থাপন প্রয়োগ করার চেষ্টা করি। ফলাফলটি একটি সমীকরণ হতে পারে যা সহজেই সমাধান করা যায়। প্রায়শই - বর্গক্ষেত্র। অথবা ভগ্নাংশ, যা একটি বর্গক্ষেত্রেও হ্রাস পায়।
4. সূচকীয় সমীকরণ সফলভাবে সমাধান করার জন্য, আপনাকে "দৃষ্টি দ্বারা" কিছু সংখ্যার ডিগ্রী জানতে হবে।
যথারীতি, পাঠের শেষে আপনাকে একটু সমাধান করার জন্য আমন্ত্রণ জানানো হয়।) নিজের থেকে। সহজ থেকে জটিল।
সূচকীয় সমীকরণগুলি সমাধান করুন:
অধিকতর কঠিন:
2 x + 3 - 2 x + 2 - 2 x \u003d 48
9 x - 8 3 x = 9
2 x - 2 0.5 x + 1 - 8 = 0
শিকড়ের পণ্য খুঁজুন:
2 3-x + 2 x = 9
ঘটেছিলো?
ঠিক আছে, তারপর সবচেয়ে জটিল উদাহরণ (এটি সমাধান করা হয়েছে, তবে, মনের মধ্যে ...):
7 0.13x + 13 0.7x+1 + 2 0.5x+1 = -3
আরো আকর্ষণীয় কি? তাহলে এখানে আপনার জন্য একটি খারাপ উদাহরণ। বেশ বর্ধিত অসুবিধা উপর টানা. আমি এই উদাহরণে ইঙ্গিত দেব যে, সমস্ত গাণিতিক কাজগুলি সমাধান করার জন্য চাতুর্য এবং সর্বজনীন নিয়ম সংরক্ষণ করে।)
2 5x-1 3 3x-1 5 2x-1 = 720 x
একটি উদাহরণ সহজ, শিথিলকরণের জন্য):
9 2 x - 4 3 x = 0
এবং মিষ্টিদ্রব্যের জন্য. সমীকরণের মূলের যোগফল নির্ণয় কর:
x 3 x - 9x + 7 3 x - 63 = 0
হ্যা হ্যা! এটি একটি মিশ্র টাইপ সমীকরণ! যা আমরা এই পাঠে বিবেচনা করিনি। এবং তাদের কী বিবেচনা করতে হবে, তাদের সমাধান করা দরকার!) এই পাঠটি সমীকরণটি সমাধান করার জন্য যথেষ্ট। ওয়েল, বুদ্ধিমত্তা প্রয়োজন ... এবং হ্যাঁ, সপ্তম শ্রেণী আপনাকে সাহায্য করবে (এটি একটি ইঙ্গিত!)
উত্তর (অব্যবস্থায়, সেমিকোলন দ্বারা পৃথক):
এক; 2; 3; চার কোন সমাধান নেই; 2; -2; -5; চার 0
সবকিছু কি সফল? চমৎকার।
একটি সমস্যা আছে? সমস্যা নেই! বিশেষ ধারা 555-এ, এই সমস্ত সূচকীয় সমীকরণগুলি বিস্তারিত ব্যাখ্যা সহ সমাধান করা হয়েছে। কি, কেন, কেন। এবং, অবশ্যই, সমস্ত ধরণের সূচকীয় সমীকরণের সাথে কাজ করার জন্য অতিরিক্ত মূল্যবান তথ্য রয়েছে। শুধু এগুলো দিয়েই নয়।)
বিবেচনা করার জন্য একটি শেষ মজার প্রশ্ন। এই পাঠে, আমরা সূচকীয় সমীকরণ নিয়ে কাজ করেছি। কেন আমি এখানে ODZ সম্পর্কে একটি শব্দ বলিনি?সমীকরণে, এটি একটি খুব গুরুত্বপূর্ণ জিনিস, যাইহোক ...
আপনি যদি এই সাইটটি পছন্দ করেন ...
যাইহোক, আমার কাছে আপনার জন্য আরও কয়েকটি আকর্ষণীয় সাইট রয়েছে।)
আপনি উদাহরণ সমাধানের অনুশীলন করতে পারেন এবং আপনার স্তর খুঁজে বের করতে পারেন। তাত্ক্ষণিক যাচাইকরণের সাথে পরীক্ষা করা হচ্ছে। শেখা - আগ্রহ সহ!)
আপনি ফাংশন এবং ডেরিভেটিভের সাথে পরিচিত হতে পারেন।









 পিছনে এগিয়ে
পিছনে এগিয়ে
মনোযোগ! স্লাইড প্রিভিউ শুধুমাত্র তথ্যগত উদ্দেশ্যে এবং উপস্থাপনার সম্পূর্ণ সীমার প্রতিনিধিত্ব নাও করতে পারে। আপনি যদি এই কাজটিতে আগ্রহী হন তবে দয়া করে সম্পূর্ণ সংস্করণটি ডাউনলোড করুন।
পাঠের ধরন
: জ্ঞান, দক্ষতা এবং ক্ষমতার সাধারণীকরণ এবং জটিল প্রয়োগের উপর একটি পাঠ "সূচকীয় সমীকরণ এবং সেগুলি সমাধানের উপায়" বিষয়ে।পাঠের লক্ষ্য।
সরঞ্জাম:
কম্পিউটার এবং মাল্টিমিডিয়া প্রজেক্টর।পাঠ ব্যবহার করে তথ্য প্রযুক্তি : পাঠের জন্য পদ্ধতিগত সমর্থন - মাইক্রোসফ্ট পাওয়ার পয়েন্টে উপস্থাপনা।
ক্লাস চলাকালীন
প্রতিটি দক্ষতা কঠোর পরিশ্রমের সাথে আসে।
আমি পাঠের লক্ষ্য নির্ধারণ করা(স্লাইড নম্বর 2 )
এই পাঠে, আমরা "সূচকীয় সমীকরণ, তাদের সমাধান" বিষয়টিকে সংক্ষিপ্ত এবং সাধারণীকরণ করব। আসুন এই বিষয়ে বিভিন্ন বছরের পরীক্ষার সাধারণ কাজগুলির সাথে পরিচিত হই।
সূচকীয় সমীকরণ সমাধানের জন্য কাজগুলি USE কার্যগুলির যে কোনও অংশে পাওয়া যেতে পারে। অংশে " AT" সাধারণত সহজতম সূচকীয় সমীকরণগুলি সমাধান করার প্রস্তাব দেয়। অংশে " থেকে " আপনি আরও জটিল সূচকীয় সমীকরণগুলি পূরণ করতে পারেন, যার সমাধানটি সাধারণত টাস্কের একটি ধাপ।
উদাহরণ স্বরূপ ( স্লাইড নম্বর 3 ).
- ব্যবহার - 2007
B 4 - রাশিটির বৃহত্তম মান নির্ণয় কর x y, কোথায় ( এক্স; এ) হল সিস্টেমের সমাধান:

B 1 - সমীকরণ সমাধান করুন:
ক) এক্স 6 3এক্স – 36 6 3এক্স = 0;
খ) 4 এক্স +1 + 8 4এক্স= 3.
B 4 - রাশিটির মান নির্ণয় কর x + y, কোথায় ( এক্স; এ) হল সিস্টেমের সমাধান:

- ব্যবহার - 2010

২. মৌলিক জ্ঞান আপডেট করা। পুনরাবৃত্তি
(স্লাইড #4 - 6 ক্লাস উপস্থাপনা)পর্দা দেখানো হয় তাত্ত্বিক উপাদানের রেফারেন্স সারাংশ এই বিষয়ে.
নিম্নলিখিত প্রশ্ন আলোচনা করা হয়:
- কি সমীকরণ বলা হয় নির্দেশক?
- সেগুলি সমাধানের প্রধান উপায়গুলির নাম বলুন। তাদের প্রকারের উদাহরণ দাও ( স্লাইড নম্বর 4 )
- ফর্মের সহজতম সূচকীয় সমীকরণগুলি সমাধান করতে কোন উপপাদ্য ব্যবহার করা হয়: এবং f(x) = a g(x)?
- সূচকীয় সমীকরণ সমাধানের জন্য অন্য কোন পদ্ধতি বিদ্যমান? ( স্লাইড নম্বর 5 )
(প্রতিটি পদ্ধতির জন্য প্রস্তাবিত সমীকরণগুলি স্ব-সমাধান করুন এবং স্লাইডটি ব্যবহার করে একটি স্ব-পরীক্ষা করুন)
- ফ্যাক্টরাইজেশন পদ্ধতি (এর সাথে ক্ষমতার বৈশিষ্ট্যের উপর ভিত্তি করে একই ঘাঁটি, অভ্যর্থনা: সর্বনিম্ন সূচক সহ ডিগ্রীটি বন্ধনী থেকে নেওয়া হয়)।
- সমজাতীয় সূচকীয় সমীকরণগুলি সমাধান করার সময় শূন্য ব্যতীত অন্য একটি সূচকীয় রাশি দ্বারা ভাগের গ্রহণ (গুণ) .
- পরামর্শ:
-
মন্তব্য দ্বারা অনুসরণ করা শেষ দুটি পদ্ধতির সাথে সমীকরণ সমাধান করা
(স্লাইড নম্বর 6 ).
. 4 এক্স+ 1 – 2 4 এক্স– 2 = 124, 4 এক্স– 2 (4 3 - 2) = 124, 4 এক্স– 2 62 = 124,4 এক্স– 2 = 2, 4 এক্স– 2 = 4 0,5 , এক্স– 2 = 0,5, x = 2,5 .
2 2 2x – 3 2 এক্স 5এক্স - 5 5 2এক্স= 0¦: 5 2 এক্স 0,2 (2/5) 2x - 3 (2/5) এক্স - 5 = 0,
t = (2/5) x, t > 0, 2t 2 - 3টি- 5 = 0,t= -1(?...), t = 5/2; 5/2 = (2/5) x, এক্স= ?...
III. ইউএসই টাস্ক 2010 সমাধান করা
শিক্ষার্থীরা 3 নং স্লাইডে পাঠের শুরুতে প্রস্তাবিত কাজগুলি স্বাধীনভাবে সমাধান করে, সমাধানের নির্দেশাবলী ব্যবহার করে, তাদের সিদ্ধান্ত প্রক্রিয়া এবং উপস্থাপনা ব্যবহার করে তাদের উত্তরগুলি পরীক্ষা করে ( স্লাইড নম্বর 7) কাজের প্রক্রিয়ায়, সমাধানের বিকল্প এবং পদ্ধতিগুলি নিয়ে আলোচনা করা হয়, সমাধানের সম্ভাব্য ত্রুটিগুলির প্রতি মনোযোগ আকর্ষণ করা হয়।
: ক) ৭ এক্স– 2 = 49, খ) (1/6) 12 - 7 এক্স = 36. উত্তর: ক) এক্স= 4, খ) এক্স = 2. : 4 এক্স 2 + 3এক্স – 2 - 0,5 2x2 + 2এক্স- 1 \u003d 0। (আপনি 0.5 \u003d 4 - 0.5 প্রতিস্থাপন করতে পারেন)সমাধান. ,
এক্স 2 + 3এক্স – 2 = -এক্স 2 - 4এক্স + 0,5 …
উত্তর: এক্স= -5/2, এক্স = 1/2.
: 5 5 গ্রাম y+ 4 = 5 -tg y, cos এ y< 0.একটি সিদ্ধান্তের জন্য পরামর্শ
. 5 5 tg y+ 4 = 5 -tg y 5 tg y 0,5 5 2 গ্রাম y+ 4 5 tg y- 1 = 0. চলুন এক্স= 5 টি গ্রাম y , …
5 টি গ্রাম y = -1 (?...), 5 টি গ্রাম y= 1/5.
যেহেতু tg y= -1 এবং cos y< 0, তারপর এ II স্থানাঙ্ক কোয়ার্টার
উত্তর: এ= 3/4 + 2k, k এন.
IV হোয়াইটবোর্ড সহযোগিতা
উচ্চ স্তরের শেখার কাজটি বিবেচনা করা হয় - স্লাইড নম্বর 8. এই স্লাইডের সাহায্যে, শিক্ষক এবং ছাত্রদের মধ্যে একটি সংলাপ হয়, যা সমাধানের বিকাশে অবদান রাখে।
- কি প্যারামিটারে ক সমীকরণ 2 2 এক্স – 3 2 এক্স + ক 2 – 4ক= 0 এর দুটি মূল আছে?দিন t= 2 এক্স, কোথায় t > 0 . আমরা পেতে t 2 – 3t + (ক 2 – 4ক) = 0 .
এক). যেহেতু সমীকরণের দুটি মূল আছে, তারপর D > 0;
2)। কারণ t 1,2 > 0, তারপর t 1 t 2 > 0, অর্থাৎ ক 2 – 4ক> 0 (?...).

উত্তর: ক(– 0.5; 0) বা (4; 4.5)।
V. যাচাইকরণের কাজ
(স্লাইড নম্বর 9 )শিক্ষার্থীরা পারফর্ম করে যাচাইকরণের কাজলিফলেটগুলিতে, আত্ম-নিয়ন্ত্রণ অনুশীলন করা এবং একটি উপস্থাপনার সাহায্যে সম্পাদিত কাজের স্ব-মূল্যায়ন, বিষয়টিতে নিজেকে জাহির করে। তারা স্বাধীনভাবে ওয়ার্কবুকগুলিতে করা ভুলের উপর ভিত্তি করে জ্ঞান নিয়ন্ত্রণ এবং সংশোধন করার জন্য একটি প্রোগ্রাম নির্ধারণ করে। সম্পূর্ণ স্বাধীন কাজ সহ শীটগুলি যাচাইয়ের জন্য শিক্ষকের কাছে হস্তান্তর করা হয়।
আন্ডারলাইন করা সংখ্যাগুলি মৌলিক, যাদের একটি তারকাচিহ্ন আছে তারা উন্নত।

সমাধান এবং উত্তর.
3. 2 এক্স– 1 (5 2 4 - 4) = 19, 2 এক্স– 1 76 = 19, 2 এক্স– 1 = 1/4, 2 এক্স– 1 = 2 – 2 , এক্স– 1 = -2,
x = -1.
4 *.3 9 x = 2 3 এক্স 5এক্স+ 5 25 এক্স | : 25 এক্স ,
3 (9/25) x = 2 (3/5) এক্স+ 5,
3 (9/27) এক্স = 2 (3/5) এক্স + 5 = 0,
3 (3/5) 2এক্স – 2 (3/5) এক্স - 5 = 0,…, (3/5) এক্স = -1 (উপযুক্ত নয়),
(3/5) এক্স = 5, x = -1.
VI. বাড়ির কাজ
(স্লাইড নম্বর 10 )- § 11, 12 পুনরাবৃত্তি করুন।
- ইউনিফাইড স্টেট এক্সাম 2008 - 2010 এর উপকরণগুলি থেকে, বিষয়ের উপর কাজগুলি নির্বাচন করুন এবং সেগুলি সমাধান করুন।
- হোম টেস্ট কাজ :

এই পাঠটি তাদের জন্য যারা সবেমাত্র সূচকীয় সমীকরণ শিখতে শুরু করেছেন। সর্বদা হিসাবে, আসুন একটি সংজ্ঞা এবং সহজ উদাহরণ দিয়ে শুরু করা যাক।
আপনি যদি এই পাঠটি পড়ছেন, তাহলে আমি সন্দেহ করি যে আপনি ইতিমধ্যেই সহজতম সমীকরণ - রৈখিক এবং বর্গাকার: $56x-11=0$ সম্পর্কে অন্তত একটি ন্যূনতম বোঝাপড়া করেছেন। $((x)^(2))+5x+4=0$; $((x)^(2))-12x+32=0$ ইত্যাদি। এখন যে বিষয়ে আলোচনা করা হবে তাতে "ঝুলে" না যাওয়ার জন্য এই জাতীয় নির্মাণগুলি সমাধান করতে সক্ষম হওয়া একেবারে প্রয়োজনীয়।
সুতরাং, সূচকীয় সমীকরণ। আমি আপনাকে কয়েকটি উদাহরণ দিই:
\[(2)^(x))=4;\quad ((5)^(2x-3))=\frac(1)(25);\quad ((9)^(x))=- ৩\]
তাদের মধ্যে কিছু আপনার কাছে আরও জটিল মনে হতে পারে, তাদের মধ্যে কিছু, বিপরীতভাবে, খুব সহজ। কিন্তু এগুলি সবগুলি একটি গুরুত্বপূর্ণ বৈশিষ্ট্য দ্বারা একত্রিত: তারা একটি সূচকীয় ফাংশন $f\left(x \right)=((a)^(x))$ ধারণ করে। সুতরাং, আমরা সংজ্ঞা প্রবর্তন:
একটি সূচকীয় সমীকরণ হল যে কোনো সমীকরণ যাতে একটি সূচকীয় ফাংশন থাকে, যেমন $(a)^(x))$ এর একটি অভিব্যক্তি। নির্দিষ্ট ফাংশন ছাড়াও, এই জাতীয় সমীকরণগুলিতে অন্য যেকোন বীজগাণিতিক গঠন থাকতে পারে - বহুপদ, মূল, ত্রিকোণমিতি, লগারিদম ইত্যাদি।
তাহলে ঠিক আছে। সংজ্ঞা বুঝেছেন। এখন প্রশ্ন হল: কিভাবে এই সমস্ত ফালতু সমাধান করা যায়? উত্তর একই সময়ে সহজ এবং জটিল উভয়ই।
আসুন সুসংবাদ দিয়ে শুরু করা যাক: অনেক শিক্ষার্থীর সাথে আমার অভিজ্ঞতা থেকে, আমি বলতে পারি যে তাদের বেশিরভাগের জন্য, সূচকীয় সমীকরণগুলি একই লগারিদমের চেয়ে অনেক সহজ, এবং আরও বেশি ত্রিকোণমিতি।
তবে একটি খারাপ খবরও রয়েছে: কখনও কখনও সমস্ত ধরণের পাঠ্যপুস্তক এবং পরীক্ষার জন্য সমস্যাগুলির সংকলনকারীরা "অনুপ্রেরণা" দ্বারা পরিদর্শন করা হয় এবং তাদের ড্রাগ-স্ফীত মস্তিষ্ক এমন নৃশংস সমীকরণ তৈরি করতে শুরু করে যে এটি কেবলমাত্র শিক্ষার্থীদের সমাধান করাই সমস্যাযুক্ত নয় - এমনকি অনেক শিক্ষক এ ধরনের সমস্যায় আটকে পড়েন।
যাইহোক, আসুন দু: খিত জিনিস সম্পর্কে কথা বলা না. এবং আসুন সেই তিনটি সমীকরণে ফিরে যাই যা গল্পের একেবারে শুরুতে দেওয়া হয়েছিল। আসুন তাদের প্রতিটি সমাধান করার চেষ্টা করি।
প্রথম সমীকরণ: $((2)^(x))=4$। আচ্ছা, 4 নম্বর পেতে হলে 2 নম্বরটিকে কোন শক্তিতে তুলতে হবে? সম্ভবত দ্বিতীয়? সর্বোপরি, $((2)^(2))=2\cdot 2=4$ — এবং আমরা সঠিক সংখ্যাগত সমতা পেয়েছি, যেমন প্রকৃতপক্ষে $x=2$। আচ্ছা, ধন্যবাদ, ক্যাপ, কিন্তু এই সমীকরণটি এত সহজ যে এমনকি আমার বিড়ালও এটি সমাধান করতে পারে। :)
আসুন নিম্নলিখিত সমীকরণটি দেখি:
\[(5)^(2x-3))=\frac(1)(25)\]
কিন্তু এখানে এটা একটু বেশি কঠিন। অনেক ছাত্র জানে যে $((5)^(2))=25$ হল গুণের সারণী। কেউ কেউ সন্দেহ করে যে $((5)^(-1))=\frac(1)(5)$ মূলত ঋণাত্মক সূচকের সংজ্ঞা (সূত্রের অনুরূপ $((a)^(-n))= \ frac(1)(((a)^(n)))$)।
অবশেষে, শুধুমাত্র কিছু নির্বাচিত অনুমান যে এই তথ্যগুলিকে একত্রিত করা যেতে পারে এবং আউটপুট হল নিম্নলিখিত ফলাফল:
\[\frac(1)(25)=\frac(1)(((5)^(2)))=(5)^(-2))\]
সুতরাং, আমাদের মূল সমীকরণটি নিম্নরূপ পুনরায় লেখা হবে:
\[(5)^(2x-3))=\frac(1)(25)\Rightarrow ((5)^(2x-3))=((5)^(-2))\]
এবং এখন এটি ইতিমধ্যে সম্পূর্ণরূপে সমাধান করা হয়েছে! সমীকরণের বাম দিকে একটি সূচকীয় ফাংশন রয়েছে, সমীকরণের ডানদিকে একটি সূচকীয় ফাংশন রয়েছে, অন্য কোথাও সেগুলি ছাড়া কিছুই নেই। অতএব, ঘাঁটিগুলি "বাতিল" করা এবং নির্বোধভাবে সূচকগুলি সমান করা সম্ভব:
আমরা সবচেয়ে সহজ রৈখিক সমীকরণ পেয়েছি যা যেকোনো শিক্ষার্থী মাত্র কয়েক লাইনে সমাধান করতে পারে। ঠিক আছে, চার লাইনে:
\[\begin(align)& 2x-3=-2 \\& 2x=3-2 \\& 2x=1 \\& x=\frac(1)(2) \\\end(align)\]
শেষ চারটি লাইনে কী ঘটেছে তা যদি আপনি বুঝতে না পারেন তবে "রৈখিক সমীকরণ" বিষয়ে ফিরে যেতে ভুলবেন না এবং এটি পুনরাবৃত্তি করুন। কারণ এই বিষয়ের একটি স্পষ্ট আত্তীকরণ ছাড়া, সূচকীয় সমীকরণগুলি গ্রহণ করা আপনার পক্ষে খুব তাড়াতাড়ি।
\[(9)^(x))=-3\]
আচ্ছা, আপনি কিভাবে সিদ্ধান্ত নেন? প্রথম চিন্তা: $9=3\cdot 3=((3)^(2))$, তাই মূল সমীকরণটি এভাবে পুনরায় লেখা যেতে পারে:
\[(\left(((3)^(2)) \right))^(x))=-3\]
তারপরে আমরা স্মরণ করি যে যখন একটি শক্তিতে একটি ডিগ্রি বাড়ানো হয়, তখন সূচকগুলি গুণিত হয়:
\[((\left(((3)^(2)) \right))^(x))=((3)^(2x))\Rightarrow ((3)^(2x))=-(( 3)^(1))\]
\[\begin(align)& 2x=-1 \\& x=-\frac(1)(2) \\\end(align)\]
এবং এই ধরনের সিদ্ধান্তের জন্য, আমরা একটি সৎভাবে প্রাপ্য ডিউস পেতে পারি। কারণ আমরা, একটি পোকেমনের সমতা সহ, এই তিনজনের শক্তিতে তিনজনের সামনে বিয়োগ চিহ্ন পাঠিয়েছিলাম। এবং আপনি তা করতে পারবেন না. আর এই কারণে. ট্রিপলের বিভিন্ন ক্ষমতার দিকে নজর দিন:
\[\begin(ম্যাট্রিক্স) ((3)^(1))=3& ((3)^(-1))=\frac(1)(3)& ((3)^(\frac(1)) 2)))=\sqrt(3) \\ ((3)^(2))=9& ((3)^(-2))=\frac(1)(9)& ((3)^(\ frac(1)(3)))=\sqrt(3) \\ ((3)^(3))=27& ((3)^(-3))=\frac(1)(27)& (( 3)^(-\frac(1)(2)))=\frac(1)(\sqrt(3)) \\\end(ম্যাট্রিক্স)\]
এই ট্যাবলেটটি সংকলন করার সাথে সাথে আমি বিকৃত করিনি: আমি ইতিবাচক ডিগ্রি, এবং নেতিবাচক এবং এমনকি ভগ্নাংশকে বিবেচনা করেছি ... আচ্ছা, এখানে অন্তত একটি নেতিবাচক সংখ্যা কোথায়? তিনি না! এবং এটি হতে পারে না, কারণ সূচকীয় ফাংশন $y=((a)^(x))$, প্রথমত, সর্বদা শুধুমাত্র ধনাত্মক মান নেয় (আপনি একটিকে যতই গুণ করুন বা দুটি দিয়ে ভাগ করুন না কেন, এটি এখনও একটি হবে ধনাত্মক সংখ্যা), এবং দ্বিতীয়ত, এই ধরনের একটি ফাংশনের ভিত্তি, সংখ্যা $a$, সংজ্ঞা অনুসারে একটি ধনাত্মক সংখ্যা!
আচ্ছা, তাহলে কিভাবে সমীকরণটি সমাধান করবেন $((9)^(x))=-3$? না, কোন শিকড় নেই। এবং এই অর্থে, সূচকীয় সমীকরণগুলি চতুর্ভুজ সমীকরণগুলির সাথে খুব সাদৃশ্যপূর্ণ - কোনও মূলও থাকতে পারে না। কিন্তু যদি দ্বিঘাত সমীকরণে শিকড়ের সংখ্যা বৈষম্যকারী দ্বারা নির্ধারিত হয় (বৈষম্যকারী ধনাত্মক - 2 মূল, ঋণাত্মক - কোন মূল নেই), তাহলে সূচকীয় সমীকরণে এটি সবই সমান চিহ্নের ডানদিকের উপর নির্ভর করে।
এইভাবে, আমরা মূল উপসংহার তৈরি করি: $((a)^(x))=b$ ফর্মের সহজতম সূচকীয় সমীকরণের একটি রুট আছে যদি এবং শুধুমাত্র যদি $b \gt 0$ থাকে। এই সহজ সত্যটি জেনে, আপনি সহজেই নির্ধারণ করতে পারেন যে আপনার কাছে প্রস্তাবিত সমীকরণটির শিকড় আছে কি না। সেগুলো. এটি কি আদৌ সমাধান করা বা অবিলম্বে লিখুন যে কোনও শিকড় নেই।
এই জ্ঞান আমাদের অনেকবার সাহায্য করবে যখন আমাদের আরও জটিল সমস্যা সমাধান করতে হবে। ইতিমধ্যে, পর্যাপ্ত লিরিক্স - এটি সূচকীয় সমীকরণগুলি সমাধানের জন্য মৌলিক অ্যালগরিদম অধ্যয়ন করার সময়।
সূচকীয় সমীকরণগুলি কীভাবে সমাধান করবেন
সুতরাং, এর সমস্যা প্রণয়ন করা যাক. সূচকীয় সমীকরণটি সমাধান করার জন্য এটি প্রয়োজনীয়:
\[(a)^(x))=b,\quad a,b \gt 0\]
আমরা আগে ব্যবহার করা "নিষ্পাপ" অ্যালগরিদম অনুসারে, $a$ নম্বরটির শক্তি হিসাবে $b$ সংখ্যাটি উপস্থাপন করা প্রয়োজন:
উপরন্তু, যদি ভেরিয়েবলের পরিবর্তে $x$ কোনো এক্সপ্রেশন থাকে, তাহলে আমরা একটি নতুন সমীকরণ পাব, যা ইতিমধ্যেই সমাধান করা যেতে পারে। উদাহরণ স্বরূপ:
\[\begin(align)& ((2)^(x))=8\Rightarrow ((2)^(x))=((2)^(3))\Rightarrow x=3; \\& ((3)^(-x))=81\Rightarrow(3)^(-x))=((3)^(4))\Rightarrow -x=4\Rightarrow x=-4; \\& ((5)^(2x))=125\Rightarrow ((5)^(2x))=(5)^(3))\Rightarrow 2x=3\Rightarrow x=\frac(3)( 2)। \\\শেষ(সারিবদ্ধ)\]
এবং অদ্ভুতভাবে যথেষ্ট, এই স্কিমটি প্রায় 90% ক্ষেত্রে কাজ করে। তাহলে অন্য 10% সম্পর্কে কি? অবশিষ্ট 10% হল ফর্মের সামান্য "সিজোফ্রেনিক" সূচকীয় সমীকরণ:
\[(2)^(x))=3;\quad ((5)^(x))=15;\quad ((4)^(2x))=11\]
3 পেতে আপনার কোন শক্তিতে 2 বাড়াতে হবে? প্রথমে? কিন্তু না: $((2)^(1))=2$ যথেষ্ট নয়। দ্বিতীয়টিতে? উভয়ই: $((2)^(2))=4$ খুব বেশি নয়। তখন কি?
জ্ঞানী শিক্ষার্থীরা সম্ভবত ইতিমধ্যে অনুমান করেছে: এই জাতীয় ক্ষেত্রে, যখন "সুন্দরভাবে" সমাধান করা অসম্ভব, "ভারী কামান" কেসের সাথে সংযুক্ত থাকে - লগারিদম। আমি আপনাকে মনে করিয়ে দিই যে লগারিদম ব্যবহার করে, যে কোনও ধনাত্মক সংখ্যাকে অন্য কোনও ধনাত্মক সংখ্যার শক্তি হিসাবে উপস্থাপন করা যেতে পারে (একটি বাদে):
এই সূত্র মনে আছে? আমি যখন আমার ছাত্রদের লগারিদম সম্পর্কে বলি, তখন আমি আপনাকে সবসময় সতর্ক করি: এই সূত্রটি (এটি মৌলিক লগারিদমিক পরিচয় বা, যদি আপনি চান, লগারিদমের সংজ্ঞা) আপনাকে দীর্ঘ সময়ের জন্য তাড়িত করবে এবং সবচেয়ে বেশি "উত্থান" করবে অপ্রত্যাশিত জায়গা। ওয়েল, তিনি প্রকাশ. আসুন আমাদের সমীকরণ এবং এই সূত্রটি দেখি:
\[\begin(align)& ((2)^(x))=3 \\& a=(b)^((\log )_(b))a)) \\\end(সারিবদ্ধ) \]
যদি আমরা ধরে নিই যে $a=3$ হল ডানদিকের আমাদের আসল সংখ্যা, এবং $b=2$ হল সূচকীয় ফাংশনের একেবারে ভিত্তি যার জন্য আমরা ডান দিকটি কমাতে চাই, আমরা নিম্নলিখিতগুলি পাব:
\[\begin(align)& a=(b)^((\log )_(b))a))\Rightarrow 3=(2)^(((\log )_(2))3 )); \\& ((2)^(x))=3\Rightarrow ((2)^(x))=((2)^(((\log )_(2))3))\Rightarrow x=( (\ লগ )_(2))3. \\\শেষ(সারিবদ্ধ)\]
আমরা একটি সামান্য অদ্ভুত উত্তর পেয়েছি: $x=((\log )_(2))3$। অন্য কোনও কাজে, এই জাতীয় উত্তর দিয়ে, অনেকে সন্দেহ করবে এবং তাদের সমাধানটি দুবার পরীক্ষা করতে শুরু করবে: কোথাও ভুল থাকলে কী হবে? আমি আপনাকে খুশি করতে তাড়াহুড়ো করছি: এখানে কোন ত্রুটি নেই, এবং সূচকীয় সমীকরণের মূলে লগারিদমগুলি বেশ সাধারণ পরিস্থিতি। তাই এটি ব্যবহার করতে পারেন. :)
এখন আমরা সাদৃশ্য দ্বারা অবশিষ্ট দুটি সমীকরণ সমাধান করি:
\[\শুরু(সারিবদ্ধ)& ((5)^(x))=15\Rightarrow ((5)^(x))=((5)^((\log )_(5))15)) \Rightarrow x=((\log )_(5))15; \\& ((4)^(2x))=11\Rightarrow ((4)^(2x))=((4)^(((\log )_(4))11))\Rightarrow 2x=( (\log )_(4))11\Rightarrow x=\frac(1)(2)((\log )_(4))11. \\\শেষ(সারিবদ্ধ)\]
এখানেই শেষ! যাইহোক, শেষ উত্তরটি ভিন্নভাবে লেখা যেতে পারে:
আমরাই লগারিদমের যুক্তিতে গুণকের প্রবর্তন করেছি। কিন্তু বেসে এই ফ্যাক্টর যোগ করা থেকে কেউ আমাদের বাধা দেয় না:
তদুপরি, তিনটি বিকল্পই সঠিক - এগুলি একই সংখ্যা লেখার বিভিন্ন রূপ মাত্র। কোনটি বেছে নেবেন এবং এই সিদ্ধান্তে লিখবেন তা আপনার উপর নির্ভর করে।
এইভাবে, আমরা $(a)^(x))=b$ ফর্মের যেকোনো সূচকীয় সমীকরণ সমাধান করতে শিখেছি, যেখানে $a$ এবং $b$ সংখ্যাগুলি কঠোরভাবে ধনাত্মক। যাইহোক, আমাদের বিশ্বের কঠোর বাস্তবতা এমন যে এই ধরনের সহজ কাজগুলি খুব কমই আপনার সাথে দেখা হবে। আরো প্রায়ই আপনি এই মত কিছু দেখতে পাবেন:
\[\begin(align)& ((4)^(x))+((4)^(x-1))=(4)^(x+1))-11; \\& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2,7)^(1-x))=0.09। \\\শেষ(সারিবদ্ধ)\]
আচ্ছা, আপনি কিভাবে সিদ্ধান্ত নেন? এটা কি আদৌ সমাধান করা যাবে? এবং যদি তাই হয়, কিভাবে?
আতঙ্ক নেই। এই সমস্ত সমীকরণগুলি দ্রুত এবং সহজভাবে সেই সহজ সূত্রগুলিতে হ্রাস করা হয় যা আমরা ইতিমধ্যে বিবেচনা করেছি। বীজগণিত কোর্সের কয়েকটি কৌশল মনে রাখার জন্য আপনাকে কেবল জানতে হবে। এবং অবশ্যই, এখানে ডিগ্রি নিয়ে কাজ করার কোনও নিয়ম নেই। আমি এখন এই সব সম্পর্কে কথা বলতে হবে. :)
সূচকীয় সমীকরণের রূপান্তর
মনে রাখা প্রথম জিনিসটি হল যে কোনও সূচকীয় সমীকরণ, তা যত জটিলই হোক না কেন, একটি উপায় বা অন্য একটি সহজ সমীকরণে নামিয়ে আনতে হবে - যেগুলি আমরা ইতিমধ্যে বিবেচনা করেছি এবং আমরা জানি কিভাবে সমাধান করতে হয়। অন্য কথায়, যেকোনো সূচকীয় সমীকরণ সমাধানের স্কিমটি নিম্নরূপ:
- মূল সমীকরণটি লিখ। যেমন: $((4)^(x))+(4)^(x-1))=((4)^(x+1))-11$;
- কিছু বোকা বিষ্ঠা করুন. অথবা এমনকি "সমীকরণ রূপান্তর" বলা কিছু বাজে কথা;
- আউটপুটে, $((4)^(x))=4$ বা এরকম অন্য কিছুর মত সহজতম এক্সপ্রেশন পান। তদুপরি, একটি প্রাথমিক সমীকরণ একবারে এরকম বেশ কয়েকটি অভিব্যক্তি দিতে পারে।
প্রথম পয়েন্টের সাথে, সবকিছু পরিষ্কার - এমনকি আমার বিড়াল একটি পাতায় সমীকরণ লিখতে পারে। তৃতীয় বিন্দুর সাথেও, মনে হচ্ছে, এটি কমবেশি স্পষ্ট - আমরা ইতিমধ্যে উপরের এই জাতীয় সমীকরণগুলির একটি সম্পূর্ণ গুচ্ছ সমাধান করেছি।
কিন্তু দ্বিতীয় পয়েন্ট সম্পর্কে কি? রূপান্তর কি? কি কি কি রূপান্তর? এবং কিভাবে?
আচ্ছা, এর এটা বের করা যাক। প্রথমত, আমি নিম্নলিখিতটি উল্লেখ করতে চাই। সমস্ত সূচকীয় সমীকরণ দুটি প্রকারে বিভক্ত:
- সমীকরণটি একই বেস সহ সূচকীয় ফাংশন দ্বারা গঠিত। উদাহরণ: $((4)^(x))+(4)^(x-1))=((4)^(x+1))-11$;
- সূত্রে বিভিন্ন বেস সহ সূচকীয় ফাংশন রয়েছে। উদাহরণ: $((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x))$ এবং $((100)^(x-1) )\cdot ((2,7)^(1-x))=0.09$।
প্রথম ধরণের সমীকরণ দিয়ে শুরু করা যাক - সেগুলি সমাধান করা সবচেয়ে সহজ। এবং তাদের সমাধানে আমরা স্থিতিশীল অভিব্যক্তি নির্বাচনের মতো একটি কৌশল দ্বারা সহায়তা করব।
একটি স্থিতিশীল অভিব্যক্তি হাইলাইট করা
আসুন এই সমীকরণটি আবার দেখি:
\[(4)^(x)+(4)^(x-1))=(4)^(x+1))-11\]
আমরা কি দেখতে পাচ্ছি? চারটি বিভিন্ন ডিগ্রিতে উত্থাপিত হয়। কিন্তু এই সমস্ত শক্তি অন্য সংখ্যার সাথে $x$ পরিবর্তনশীলের সরল যোগফল। অতএব, ডিগ্রি নিয়ে কাজ করার নিয়মগুলি মনে রাখা প্রয়োজন:
\[\begin(align)& ((a)^(x+y))=((a)^(x))\cdot ((a)^(y)); \\& ((a)^(x-y))=((a)^(x)):((a)^(y))=\frac(((a)^(x)))((a) )^(y)))। \\\শেষ(সারিবদ্ধ)\]
সহজ কথায়, সূচকের যোগকে ক্ষমতার গুণে রূপান্তরিত করা যায় এবং বিয়োগ সহজেই ভাগে রূপান্তরিত হয়। আসুন আমাদের সমীকরণ থেকে শক্তিগুলিতে এই সূত্রগুলি প্রয়োগ করার চেষ্টা করি:
\[\শুরু(সারিবদ্ধ)& ((4)^(x-1))=\frac(((4)^(x)))(((4)^(1)))=(4)^ (x))\cdot \frac(1)(4); \\& ((4)^(x+1))=((4)^(x))\cdot ((4)^(1))=((4)^(x))\cdot 4। \ \\ শেষ(সারিবদ্ধ)\]
আমরা এই সত্যটিকে বিবেচনায় নিয়ে মূল সমীকরণটি পুনরায় লিখি এবং তারপরে আমরা বাম দিকের সমস্ত পদ সংগ্রহ করি:
\[\begin(align)& ((4)^(x)+((4)^(x))\cdot \frac(1)(4)=((4)^(x))\cdot 4 -এগারো; \\& ((4)^(x))+((4)^(x))\cdot \frac(1)(4)-(4)^(x))\cdot 4+11=0। \\\শেষ(সারিবদ্ধ)\]
প্রথম চারটি পদে $((4)^(x))$ এলিমেন্ট রয়েছে — আসুন এটিকে বন্ধনী থেকে বের করা যাক:
\[\begin(align)& ((4)^(x))\cdot \left(1+\frac(1)(4)-4 \right)+11=0; \\& ((4)^(x))\cdot \frac(4+1-16)(4)+11=0; \\& ((4)^(x))\cdot \left(-\frac(11)(4) \right)=-11। \\\শেষ(সারিবদ্ধ)\]
সমীকরণের উভয় অংশকে ভগ্নাংশ $-\frac(11)(4)$ দ্বারা ভাগ করতে হবে, অর্থাৎ মূলত উল্টানো ভগ্নাংশ দ্বারা গুণ করুন - $-\frac(4)(11)$। আমরা পেতে:
\[\শুরু(সারিবদ্ধ)& ((4)^(x))\cdot \left(-\frac(11)(4) \right)\cdot \left(-\frac(4)(11) \right )=-11\cdot \left(-\frac(4)(11) \right); \\& ((4)^(x))=4; \\& ((4)^(x))=((4)^(1)); \\&x=1। \\\শেষ(সারিবদ্ধ)\]
এখানেই শেষ! আমরা মূল সমীকরণটিকে সহজে কমিয়েছি এবং চূড়ান্ত উত্তর পেয়েছি।
একই সময়ে, সমাধানের প্রক্রিয়ায়, আমরা সাধারণ ফ্যাক্টর $((4)^(x))$ আবিষ্কার করেছি (এবং বন্ধনী থেকেও বের করেছি) - এটি স্থিতিশীল অভিব্যক্তি। এটি একটি নতুন ভেরিয়েবল হিসাবে মনোনীত করা যেতে পারে, অথবা আপনি এটিকে সঠিকভাবে প্রকাশ করতে এবং একটি উত্তর পেতে পারেন। যে কোনও ক্ষেত্রে, সমাধানের মূল নীতিটি নিম্নরূপ:
মূল সমীকরণে একটি চলক সম্বলিত একটি স্থিতিশীল রাশি খুঁজুন যা সমস্ত সূচকীয় ফাংশন থেকে সহজেই আলাদা করা যায়।
ভাল খবর হল যে প্রায় প্রতিটি সূচকীয় সমীকরণ এমন একটি স্থিতিশীল অভিব্যক্তি স্বীকার করে।
কিন্তু খারাপ খবরও আছে: এই ধরনের অভিব্যক্তি খুব কঠিন হতে পারে, এবং তাদের পার্থক্য করা বেশ কঠিন হতে পারে। তাহলে আসুন আরেকটি সমস্যা দেখি:
\[(5)^(x+2))+((0,2)^(-x-1))+4\cdot ((5)^(x+1))=2\]
সম্ভবত কেউ এখন একটি প্রশ্ন করবে: "পাশা, আপনি কি পাথর মেরেছেন? এখানে বিভিন্ন ঘাঁটি রয়েছে - 5 এবং 0.2। তবে আসুন বেস 0.2 দিয়ে একটি পাওয়ার রূপান্তর করার চেষ্টা করি। উদাহরণস্বরূপ, আসুন দশমিক ভগ্নাংশ থেকে পরিত্রাণ পাই, এটিকে স্বাভাবিক অবস্থায় নিয়ে আসা:
\[(0,2)^(-x-1))=((0,2)^(-\left(x+1 \right)))=((\left(\frac(2)(10) ) \right))^(-\left(x+1 \right)))=(\left(\frac(1)(5) \right))^(-\left(x+1 \right)) )\]
আপনি দেখতে পাচ্ছেন, 5 নম্বরটি এখনও উপস্থিত হয়েছে, যদিও হরটিতে। একই সময়ে, সূচকটি নেতিবাচক হিসাবে পুনরায় লেখা হয়েছিল। এবং এখন আমরা ডিগ্রি নিয়ে কাজ করার জন্য সবচেয়ে গুরুত্বপূর্ণ নিয়মগুলির একটি স্মরণ করি:
\[((a)^(-n))=\frac(1)(((a)^(n)))\Rightarrow ((\left(\frac(1)(5) \right))^( -\left(x+1 \right)))=((\left(\frac(5)(1) \right))^(x+1))=(5)^(x+1))\ ]
এখানে, অবশ্যই, আমি একটু প্রতারণা করেছি। কারণ সম্পূর্ণ বোঝার জন্য, নেতিবাচক সূচকগুলি থেকে পরিত্রাণ পাওয়ার সূত্রটি নিম্নরূপ লিখতে হয়েছিল:
\[(a)^(-n))=\frac(1)((a)^(n))=(\left(\frac(1)(a) \right))^(n) ))\Rightarrow ((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=(\left(\frac(5)(1) \ ডানদিকে)^(x+1))=((5)^(x+1))\]
অন্যদিকে, কিছুই আমাদের শুধুমাত্র একটি ভগ্নাংশের সাথে কাজ করতে বাধা দেয়নি:
\[(\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=(\left(((5)^(-1)) \ ডান))^(-\left(x+1 \right)))=((5)^(\left(-1 \right)\cdot \left(-\left(x+1 \right) \right) ))=(5)^(x+1))\]
কিন্তু এই ক্ষেত্রে, আপনাকে অন্য ডিগ্রীতে একটি ডিগ্রী বাড়াতে সক্ষম হতে হবে (আমি আপনাকে মনে করিয়ে দিচ্ছি: এই ক্ষেত্রে, সূচকগুলি যোগ করা হয়েছে)। কিন্তু আমাকে ভগ্নাংশগুলিকে "ফ্লিপ" করতে হবে না - সম্ভবত কারও পক্ষে এটি সহজ হবে। :)
যে কোনো ক্ষেত্রে, মূল সূচকীয় সমীকরণটি এইভাবে পুনরায় লেখা হবে:
\[\begin(align)& ((5)^(x+2))+((5)^(x+1))+4\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+5\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(1))\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(x+2))=2; \\& 2\cdot ((5)^(x+2))=2; \\& ((5)^(x+2))=1। \\\শেষ(সারিবদ্ধ)\]
সুতরাং দেখা যাচ্ছে যে মূল সমীকরণটি পূর্বে বিবেচিত সমীকরণের চেয়ে সমাধান করা আরও সহজ: এখানে আপনাকে একটি স্থিতিশীল অভিব্যক্তি একক করার দরকার নেই - সবকিছু নিজেই হ্রাস পেয়েছে। এটি শুধুমাত্র মনে রাখতে হবে যে $1=((5)^(0))$, যেখান থেকে আমরা পাই:
\[\begin(সারিবদ্ধ)& ((5)^(x+2))=((5)^(0)); \\&x+2=0; \\&x=-2। \\\শেষ(সারিবদ্ধ)\]
এটাই পুরো সমাধান! আমরা চূড়ান্ত উত্তর পেয়েছি: $x=-2$। একই সময়ে, আমি একটি কৌশল নোট করতে চাই যা আমাদের জন্য সমস্ত গণনাকে ব্যাপকভাবে সরল করেছে:
সূচকীয় সমীকরণে, দশমিক ভগ্নাংশ থেকে পরিত্রাণ পেতে ভুলবেন না, সেগুলিকে সাধারণের মধ্যে অনুবাদ করুন। এটি আপনাকে ডিগ্রিগুলির একই ঘাঁটিগুলি দেখতে এবং সমাধানটিকে ব্যাপকভাবে সরল করার অনুমতি দেবে।
এখন আরও জটিল সমীকরণের দিকে যাওয়া যাক যেখানে বিভিন্ন ভিত্তি রয়েছে, যেগুলি সাধারণত শক্তির সাহায্যে একে অপরের সাথে হ্রাস পায় না।
সূচক সম্পত্তি ব্যবহার করে
আমি আপনাকে মনে করিয়ে দিই যে আমাদের আরও দুটি বিশেষভাবে কঠোর সমীকরণ রয়েছে:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2,7)^(1-x))=0.09। \\\শেষ(সারিবদ্ধ)\]
এখানে প্রধান অসুবিধা হ'ল এটি স্পষ্ট নয় যে কী এবং কীসের ভিত্তিতে নেতৃত্ব দেওয়া উচিত। স্থির অভিব্যক্তি কোথায়? সাধারণ ভিত্তি কোথায়? এর কিছুই নেই।
তবে চলুন অন্য পথে যাওয়ার চেষ্টা করি। যদি কোন প্রস্তুত-তৈরি অভিন্ন ঘাঁটি না থাকে তবে আপনি উপলব্ধ ঘাঁটিগুলিকে ফ্যাক্টর করে সেগুলি খুঁজে বের করার চেষ্টা করতে পারেন।
প্রথম সমীকরণ দিয়ে শুরু করা যাক:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& 21=7\cdot 3\Rightarrow ((21)^(3x))=(\left(7\cdot 3 \right)^(3x))=((7)^(3x))\ cdot ((3)^(3x))। \\\শেষ(সারিবদ্ধ)\]
তবে আপনি বিপরীতটি করতে পারেন - 7 এবং 3 নম্বর থেকে 21 নম্বরটি তৈরি করুন। বাম দিকে এটি করা বিশেষত সহজ, যেহেতু উভয় ডিগ্রির সূচক একই:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((\left(7\cdot 3 \right))^(x+6) ))=((21)^(x+6)); \\& ((21)^(x+6))=((21)^(3x)); \\&x+6=3x; \\& 2x=6; \\&x=৩। \\\শেষ(সারিবদ্ধ)\]
এখানেই শেষ! আপনি পণ্য থেকে সূচকটি বের করেছেন এবং অবিলম্বে একটি সুন্দর সমীকরণ পেয়েছেন যা কয়েক লাইনে সমাধান করা যেতে পারে।
এখন দ্বিতীয় সমীকরণের সাথে মোকাবিলা করা যাক। এখানে সবকিছু অনেক বেশি জটিল:
\[((100)^(x-1))\cdot ((2,7)^(1-x))=0.09\]
\[((100)^(x-1))\cdot ((\left(\frac(27)(10) \right))^(1-x))=\frac(9)(100)\]
এই ক্ষেত্রে, ভগ্নাংশগুলি অপরিবর্তনীয় হতে দেখা গেছে, তবে যদি কিছু হ্রাস করা যায় তবে এটি হ্রাস করতে ভুলবেন না। এটি প্রায়শই আকর্ষণীয় ভিত্তিতে পরিণত হয় যা আপনি ইতিমধ্যে কাজ করতে পারেন।
দুর্ভাগ্যক্রমে, আমরা কিছুই নিয়ে আসিনি। কিন্তু আমরা দেখতে পাই যে পণ্যের বাম দিকের সূচকগুলি বিপরীত:
আমি আপনাকে মনে করিয়ে দিচ্ছি: সূচকে বিয়োগ চিহ্ন থেকে পরিত্রাণ পেতে, আপনাকে কেবল ভগ্নাংশটিকে "ফ্লিপ" করতে হবে। তাহলে আসুন মূল সমীকরণটি আবার লিখি:
\[\শুরু(সারিবদ্ধ)& ((100)^(x-1))\cdot ((\left(\frac(10)(27) \right))^(x-1))=\frac(9 )(100); \\& ((\left(100\cdot \frac(10)(27) \right))^(x-1))=\frac(9)(100); \\& ((\left(\frac(1000)(27) \right))^(x-1))=\frac(9)(100)। \\\শেষ(সারিবদ্ধ)\]
দ্বিতীয় লাইনে, আমরা $((a)^(x))\cdot ((b)^(x))=((\left(a\cdot b \right) নিয়ম অনুসারে পণ্য থেকে মোট ব্র্যাকেট করেছি ))^ (x))$, এবং পরবর্তীতে তারা 100 সংখ্যাটিকে একটি ভগ্নাংশ দ্বারা গুণ করেছে।
এখন লক্ষ্য করুন যে বাম দিকে (বেসে) এবং ডানদিকের সংখ্যাগুলি কিছুটা একই রকম। কিভাবে? হ্যাঁ, স্পষ্টতই: তারা একই সংখ্যার শক্তি! আমাদের আছে:
\[\শুরু(সারিবদ্ধ)&\frac(1000)(27)=\frac(((10)^(3)))((3)^(3)))=(\left(\frac( 10)(3) \right))^(3)); \\& \frac(9)(100)=\frac(((3)^(2)))((10)^(3))=((\left(\frac(3)(10) \ ডান))^(2))। \\\শেষ(সারিবদ্ধ)\]
সুতরাং, আমাদের সমীকরণটি নিম্নরূপ পুনরায় লেখা হবে:
\[(\left((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=((\left(\frac(3) )(10) \ডান))^(2))\]
\[(\left((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=((\left(\frac(10) )(3) \right))^(3\left(x-1 \right)))=(\left(\frac(10)(3) \right))^(3x-3))\]
একই সময়ে, ডানদিকে, আপনি একই বেস সহ একটি ডিগ্রিও পেতে পারেন, যার জন্য ভগ্নাংশটিকে "উল্টানো" যথেষ্ট:
\[(\left(\frac(3)(10) \right))^(2))=((\left(\frac(10)(3) \right))^(-2))\]
অবশেষে, আমাদের সমীকরণটি ফর্মটি গ্রহণ করবে:
\[\শুরু(সারিবদ্ধ) এবং ((\left(\frac(10)(3) \right))^(3x-3))=((\left(\frac(10)(3) \right)) ^(-2)); \\& 3x-3=-2; \\& 3x=1; \\& x=\frac(1)(3)। \\\শেষ(সারিবদ্ধ)\]
এটাই পুরো সমাধান। এর মূল ধারণাটি এই সত্যে ফুটে উঠেছে যে এমনকি বিভিন্ন ভিত্তি থাকা সত্ত্বেও, আমরা হুক বা ক্রুক দ্বারা এই গ্রাউন্ডগুলিকে একই স্থলে হ্রাস করার চেষ্টা করি। এতে আমরা সমীকরণের প্রাথমিক রূপান্তর এবং ক্ষমতার সাথে কাজ করার নিয়মগুলি দ্বারা সহায়তা করি।
কিন্তু কি নিয়ম এবং কখন ব্যবহার করবেন? কীভাবে বুঝবেন যে একটি সমীকরণে আপনাকে উভয় পক্ষকে কিছু দ্বারা ভাগ করতে হবে এবং অন্যটিতে - সূচকীয় ফাংশনের ভিত্তিকে ফ্যাক্টরাইজ করতে হবে?
এই প্রশ্নের উত্তর অভিজ্ঞতা দিয়ে আসবে। প্রথমে সহজ সমীকরণে আপনার হাত চেষ্টা করুন, এবং তারপর ধীরে ধীরে কাজগুলিকে জটিল করুন - এবং খুব শীঘ্রই আপনার দক্ষতা একই USE বা যেকোনো স্বাধীন/পরীক্ষামূলক কাজ থেকে যেকোনো সূচকীয় সমীকরণ সমাধান করার জন্য যথেষ্ট হবে।
এবং এই কঠিন কাজে আপনাকে সাহায্য করার জন্য, আমি একটি স্বাধীন সমাধানের জন্য আমার ওয়েবসাইটে সমীকরণের একটি সেট ডাউনলোড করার পরামর্শ দিচ্ছি। সমস্ত সমীকরণের উত্তর আছে, তাই আপনি সর্বদা নিজেকে পরীক্ষা করতে পারেন।
সাধারণভাবে, আমি আপনাকে সফল প্রশিক্ষণ কামনা করি। এবং পরবর্তী পাঠে দেখা হবে - সেখানে আমরা সত্যিই জটিল সূচকীয় সমীকরণ বিশ্লেষণ করব, যেখানে উপরে বর্ণিত পদ্ধতিগুলি আর যথেষ্ট নয়। এবং একটি সাধারণ ওয়ার্কআউট যথেষ্ট হবে না। :)
আমাদের সাইটের ইউটিউব চ্যানেলে নতুন সব ভিডিও পাঠ সম্পর্কে অবগত থাকুন।
প্রথমে, আসুন ডিগ্রী এবং তাদের বৈশিষ্ট্যগুলির মৌলিক সূত্রগুলি স্মরণ করি।
একটি সংখ্যার পণ্য কনিজেই n বার ঘটে, আমরা এই রাশিটিকে a … a=a n হিসাবে লিখতে পারি
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n / a m \u003d a n - m
শক্তি বা সূচকীয় সমীকরণ- এগুলি এমন সমীকরণ যেখানে ভেরিয়েবলগুলি শক্তিতে (বা সূচক) এবং ভিত্তি হল একটি সংখ্যা।
সূচকীয় সমীকরণের উদাহরণ:
এই উদাহরণে, সংখ্যা 6 হল ভিত্তি, এটি সর্বদা নীচে থাকে এবং পরিবর্তনশীল এক্সডিগ্রি বা পরিমাপ।
সূচকীয় সমীকরণের আরও উদাহরণ দেওয়া যাক।
2 x *5=10
16x-4x-6=0
এখন দেখা যাক কিভাবে সূচকীয় সমীকরণগুলো সমাধান করা হয়?
আসুন একটি সহজ সমীকরণ নেওয়া যাক:
2 x = 2 3
এমন উদাহরণ দিলেও মনের সমাধান করা যায়। দেখা যায় যে x=3. সর্বোপরি, বাম এবং ডান দিক সমান হওয়ার জন্য, আপনাকে x এর পরিবর্তে 3 নম্বর লাগাতে হবে।
এখন দেখা যাক কীভাবে এই সিদ্ধান্ত নেওয়া উচিত:
2 x = 2 3
x = 3
এই সমীকরণটি সমাধান করার জন্য, আমরা সরিয়ে দিয়েছি একই ভিত্তি(অর্থাৎ, deuces) এবং যা অবশিষ্ট ছিল তা লিখুন, এইগুলি ডিগ্রি। আমরা যে উত্তর খুঁজছিলাম তা পেয়েছি।
এখন আমাদের সমাধান সংক্ষিপ্ত করা যাক.
সূচকীয় সমীকরণ সমাধানের জন্য অ্যালগরিদম:
1. চেক করতে হবে একইসমীকরণের ভিত্তি ডানে এবং বামে কিনা। যদি ভিত্তি একই না হয়, আমরা এই উদাহরণটি সমাধান করার বিকল্পগুলি খুঁজছি।
2. ভিত্তিগুলি একই হওয়ার পরে, সমান করাডিগ্রী এবং ফলে নতুন সমীকরণ সমাধান.
এখন কিছু উদাহরণ সমাধান করা যাক:
এর সহজ শুরু করা যাক.
বাম এবং ডান দিকের ঘাঁটিগুলি 2 নম্বরের সমান, যার অর্থ আমরা বেসটি বাতিল করতে পারি এবং তাদের ডিগ্রি সমান করতে পারি।
x+2=4 সবচেয়ে সহজ সমীকরণ বের হয়েছে।
x=4 - 2
x=2
উত্তরঃ x=2
নিম্নলিখিত উদাহরণে, আপনি দেখতে পারেন যে ঘাঁটিগুলি আলাদা, এগুলি হল 3 এবং 9।
3 3x - 9 x + 8 = 0
শুরু করার জন্য, আমরা নয়টি ডানদিকে স্থানান্তর করি, আমরা পাই:
এখন আপনাকে একই ঘাঁটি তৈরি করতে হবে। আমরা জানি যে 9=3 2। আসুন পাওয়ার সূত্রটি ব্যবহার করি (a n) m = a nm।
3 3x \u003d (3 2) x + 8
আমরা পাই 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16
3 3x \u003d 3 2x + 16 এখন এটা স্পষ্ট যে বাম এবং ডান দিকের ঘাঁটিগুলি একই এবং তিনটির সমান, যার মানে আমরা তাদের বাতিল করতে পারি এবং ডিগ্রীগুলিকে সমান করতে পারি।
3x=2x+16 সবচেয়ে সহজ সমীকরণ পেয়েছে
3x-2x=16
x=16
উত্তরঃ x=16।
আসুন নিম্নলিখিত উদাহরণটি দেখি:
2 2x + 4 - 10 4 x \u003d 2 4
প্রথমত, আমরা ঘাঁটিগুলি দেখি, ঘাঁটি দুটি এবং চারটি আলাদা। এবং আমরা একই হতে হবে. আমরা সূত্র (a n) m = a nm অনুসারে চতুর্গুণ রূপান্তর করি।
4 x = (2 2) x = 2 2x
এবং আমরা একটি সূত্র ব্যবহার করি a n a m = a n + m:
2 2x+4 = 2 2x 2 4
সমীকরণ যোগ করুন:
2 2x 2 4 - 10 2 2x = 24
আমরা একই কারণে একটি উদাহরণ দিয়েছি। কিন্তু অন্যান্য সংখ্যা 10 এবং 24 আমাদের সাথে হস্তক্ষেপ করে তাদের সাথে কি করতে হবে? আপনি যদি ঘনিষ্ঠভাবে লক্ষ্য করেন তবে আপনি দেখতে পাবেন যে বাম দিকে আমরা 2 2x পুনরাবৃত্তি করি, এখানে উত্তরটি রয়েছে - আমরা বন্ধনীর বাইরে 2 2x রাখতে পারি:
2 2x (2 4 - 10) = 24
বন্ধনীতে অভিব্যক্তি গণনা করা যাক:
2 4 — 10 = 16 — 10 = 6
আমরা পুরো সমীকরণটি 6 দ্বারা ভাগ করি:
কল্পনা করুন 4=2 2:
2 2x \u003d 2 2 বেস একই, সেগুলি বাদ দিন এবং ডিগ্রী সমান করুন।
2x \u003d 2 সবচেয়ে সহজ সমীকরণে পরিণত হয়েছে। আমরা এটিকে 2 দ্বারা ভাগ করি, আমরা পাই
x = 1
উত্তরঃ x = 1।
আসুন সমীকরণটি সমাধান করি:
9 x - 12*3 x +27= 0
আসুন রূপান্তর করি:
9 x = (3 2) x = 3 2x
আমরা সমীকরণ পাই:
3 2x - 12 3 x +27 = 0
আমাদের ঘাঁটি একই, তিনটির সমান৷ এই উদাহরণে, এটা স্পষ্ট যে প্রথম ট্রিপলের দ্বিতীয় (শুধু x) থেকে দ্বিগুণ (2x) ডিগ্রি রয়েছে৷ এই ক্ষেত্রে, আপনি সিদ্ধান্ত নিতে পারেন প্রতিস্থাপন পদ্ধতি. ক্ষুদ্রতম ডিগ্রী সহ সংখ্যা দ্বারা প্রতিস্থাপিত হয়:
তারপর 3 2x \u003d (3 x) 2 \u003d t 2
আমরা t দিয়ে সমীকরণে x এর সাথে সমস্ত ডিগ্রি প্রতিস্থাপন করি:
t 2 - 12t + 27 \u003d 0
আমরা একটি দ্বিঘাত সমীকরণ পাই। আমরা বৈষম্যকারীর মাধ্যমে সমাধান করি, আমরা পাই:
D=144-108=36
t1 = 9
t2 = 3
পরিবর্তনশীল-এ ফিরে যান এক্স.
আমরা টি 1 নিই:
t 1 \u003d 9 \u003d 3 x
এটাই,
3 x = 9
3 x = 3 2
x 1 = 2
একটি মূল পাওয়া গেছে। আমরা টি 2 থেকে দ্বিতীয়টি খুঁজছি:
t 2 \u003d 3 \u003d 3 x
3 x = 3 1
x 2 = 1
উত্তর: x 1 \u003d 2; x 2 = 1।
সাইটে আপনি বিভাগে পারেন সিদ্ধান্ত নিতে সাহায্য করুনআপনার কোন প্রশ্ন থাকলে, আমরা অবশ্যই আপনাকে উত্তর দেব।
একটি গ্রুপে যোগ দিন