Ранг на матрицата 2x2. Намиране на ранга на матрица. Определяне на ранга на матрица

Числото r се нарича ранг на матрицата A, ако:
1) матрицата A съдържа ненулев минор от порядък r;
2) всички минорни от порядък (r + 1) и по-високи, ако съществуват, са равни на нула.
В противен случай рангът на матрицата е най-високият ред на ненулев минор.
Обозначения: rangA , r A или r .
От дефиницията следва, че r е цяло положително число. За нулева матрица рангът се счита за нула.

Възлагане на услугата. Онлайн калкулаторът е предназначен за намиране матричен ранг. Решението се запазва във формат Word и Excel. виж пример за решение.

Инструкция. Изберете измерението на матрицата, щракнете върху Напред.

Определение . Нека е дадена матрица с ранг r. Всяка минорна матрица, различна от нула и имаща порядък r, се нарича основна, а редовете и колоните на нейните компоненти се наричат основни редове и колони.
Съгласно тази дефиниция, матрицата A може да има няколко базисни минор.

Рангът на матрицата за идентичност E е n (брой редове).

Пример 1 . Дадени са две матрици, и техните непълнолетни , . Кое от тях може да се вземе за основа?
Решение. Минорното M 1 =0, така че не може да бъде основа за нито една от матриците. Минор M 2 =-9≠0 и има ред 2, така че може да се вземе като базисни матрици на A или / и B, при условие че те имат ранг, равен на 2. Тъй като detB=0 (като детерминанта с две пропорционални колони), тогава rangB=2 и M 2 могат да бъдат взети като базисен минор на матрица B. Рангът на матрица A е 3, поради факта, че detA=-27≠ 0 и следователно редът на базисния минор на тази матрица трябва да бъде 3, т.е. M 2 не е основа за матрицата A . Забележете, че матрицата A има уникален базисен минор, равен на детерминантата на матрицата A.

Теорема (за основния минор). Всеки ред (колона) на матрица е линейна комбинация от основните й редове (колони).
Следствия от теоремата.

Всички (r+1) колони (редове) на матрица с ранг r са линейно зависими.
Ако рангът на една матрица е по-малък от броя на нейните редове (колони), тогава нейните редове (колони) са линейно зависими. Ако rangA е равен на броя на неговите редове (колони), тогава редовете (колони) са линейно независими.
Детерминантата на матрица A е равна на нула, ако и само ако нейните редове (колони) са линейно зависими.
Ако към реда (колоната) на матрицата се добави друг ред (колона), умножен по произволно число, различно от нула, тогава рангът на матрицата няма да се промени.
Ако зачеркнете ред (колона) в матрицата, която е линейна комбинация от други редове (колони), тогава рангът на матрицата няма да се промени.
Рангът на матрицата е равен на максималния брой на нейните линейно независими редове (колони).
Максималният брой линейно независими редове е същият като максималния брой линейно независими колони.

Пример 2. Намерете ранга на матрица .
Решение. Въз основа на дефиницията на ранга на матрица ще търсим минор от най-висок порядък, който е различен от нула. Първо, трансформираме матрицата в по-проста форма. За да направите това, умножете първия ред на матрицата по (-2) и добавете към втория, след това го умножете по (-1) и добавете към третия.

И също така помислете за важно практическо приложение на темата: изследване на система от линейни уравнения за съвместимост.

Какъв е рангът на матрицата?

Хумористичният епиграф на статията съдържа много истина. Самата дума "ранг" обикновено се свързва с някаква йерархия, най-често с кариерната стълбица. Колкото повече знания, опит, способности, връзки и т.н. има човек. - толкова по-висока е неговата позиция и диапазон от възможности. В младежки термини, рангът се отнася до общата степен на "твърдост".

И нашите математически братя живеят по същите принципи. Да вземем на разходка няколко произволни нулеви матрици:

Нека помислим дали в матрицата само нули, тогава за какъв ранг можем да говорим? Всеки е запознат с неформалния израз "обща нула". В матричното общество всичко е абсолютно същото:

Нулев матричен рангвсеки размер е нула.

Забележка : нулевата матрица се обозначава с гръцката буква "тета"

За да разбера по-добре ранга на матрицата, по-нататък ще използвам материалите аналитична геометрия. Помислете за нула векторна нашето триизмерно пространство, което не задава определена посока и е безполезно за изграждане афинна основа. От алгебрична гледна точка координатите на даден вектор се записват матрица"едно по три" и логично (в определения геометричен смисъл)приемем, че рангът на тази матрица е нула.

Сега нека разгледаме няколко различен от нула колонни вектории редови вектори:

Всеки екземпляр има поне един ненулев елемент и това е нещо!

Рангът на всеки ненулев вектор-ред (вектор колона) е равен на единица

И най-общо казано - ако е в матрица произволни размериима поне един ненулев елемент, след което неговият ранг не по-малкоединици.

Алгебричните вектори на редове и колони са абстрактни до известна степен, така че нека се обърнем отново към геометричната асоциация. различен от нула векторзадава добре дефинирана посока в пространството и е подходящ за конструиране основа, така че рангът на матрицата ще се приеме, че е равен на единица.

Теоретична справка : в линейната алгебра векторът е елемент от векторно пространство (дефинирано чрез 8 аксиоми), което по-специално може да бъде подреден ред (или колона) от реални числа с операциите събиране и умножение с дефинирано реално число за тях. За повече информация относно векторите вижте статията Линейни трансформации.

линейно зависими(изразени един през друг). От геометрична гледна точка, вторият ред съдържа координатите на колинеарния вектор , което не напредна въпроса в строителството триизмерна основа, което е излишно в този смисъл. По този начин рангът на тази матрица също е равен на единица.

Пренаписваме координатите на векторите в колони ( транспониране на матрицата):

Какво се промени по отношение на ранга? Нищо. Колоните са пропорционални, което означава, че рангът е равен на единица. Между другото, имайте предвид, че и трите реда също са пропорционални. Те могат да бъдат идентифицирани с координатите триколинеарни вектори на равнината, от които само единполезно за изграждане на "плоска" основа. И това е в пълно съответствие с нашето геометрично чувство за ранг.

Важно твърдение следва от горния пример:

Рангът на матрица по редове е равен на ранга на матрица по колони. Вече споменах това малко в урока за ефективност методи за изчисляване на детерминанта.

Забележка : линейната зависимост на редовете води до линейна зависимост на колоните (и обратно). Но за да спестя време и по навик почти винаги ще говоря за линейната зависимост на струните.

Нека продължим да обучаваме любимия си домашен любимец. Добавете координатите на друг колинеарен вектор към матрицата в третия ред :

Той помогна ли ни в изграждането на триизмерна основа? Разбира се, че не. И трите вектора се движат напред-назад по един и същи път, а рангът на матрицата е един. Можете да вземете колкото искате колинеарни вектори, да речем 100, да поставите техните координати в матрица 100 на 3 и рангът на такъв небостъргач все още ще остане един.

Нека се запознаем с матрицата, чиито редове линейно независими. Двойка неколинеарни вектори е подходяща за конструиране на триизмерна основа. Рангът на тази матрица е два.

Какъв е рангът на матрицата? Изглежда, че линиите не са пропорционални ... така че на теория три. Въпреки това, рангът на тази матрица също е равен на две. Добавих първите два реда и записах резултата отдолу, т.е. линейно изразентрети ред през първите две. Геометрично, редовете на матрицата съответстват на координатите на три компланарни вектори, а сред тази тройка има двойка другари не-колинеарни.

Както виждаш линейна зависимоств разглежданата матрица не е очевидно и днес просто ще научим как да го доведем „до чиста вода“.

Мисля, че много хора се досещат какъв е рангът на матрицата!

Да разгледаме матрица, чиито редове линейно независими. Формират се вектори афинна основа, а рангът на тази матрица е три.

Както знаете, всеки четвърти, пети, десети вектор на триизмерното пространство ще бъде линейно изразен чрез основни вектори. Следователно, ако към матрицата се добави някакъв брой редове, тогава нейният ранг пак ще са три.

Подобни разсъждения могат да бъдат извършени за матрици с по-големи размери (ясно, вече без геометричен смисъл).

Определение : рангът на матрицата е максималният брой линейно независими редове. Или: рангът на матрицата е максималният брой линейно независими колони. Да, винаги съвпадат.

Важна практическа насока следва от горното: рангът на матрицата не надвишава минималното й измерение. Например в матрицата четири реда и пет колони. Минималното измерение е четири, следователно рангът на тази матрица със сигурност няма да надвишава 4.

Нотация: в световната теория и практика няма общоприет стандарт за определяне на ранга на матрицата, може да се намери най-често срещаният: - както се казва, англичанин пише едно, германец друго. Ето защо, въз основа на добре познатия анекдот за американския и руския ад, нека обозначим ранга на матрицата с родна дума. Например: . И ако матрицата е "безименна", от които има много, тогава можете просто да напишете .

Как да намерим ранга на матрица, използвайки минорите?

Ако нашата баба имаше пета колона в матрицата, тогава трябваше да се изчисли още един минор от 4-ти ред („синьо“, „малина“ + 5-та колона).

Заключение: максималният ред на ненулев минор е три, така че .

Може би не всички са разбрали напълно тази фраза: минорът от 4-ти порядък е равен на нула, но сред минорите от 3-ти порядък имаше ненулев един - следователно, максималният ред различен от нуламинор и равен на три.

Възниква въпросът защо не се изчисли веднага детерминантата? Е, първо, в повечето задачи матрицата не е квадратна, и второ, дори ако получите ненулева стойност, тогава задачата ще бъде отхвърлена с голяма вероятност, тъй като обикновено предполага стандартно решение отдолу нагоре. И в разглеждания пример нулевият детерминант от 4-ти ред дори ни позволява да твърдим, че рангът на матрицата е само по-малък от четири.

Трябва да призная, че аз сам измислих анализирания проблем, за да обясня по-добре метода на граничене на непълнолетните. В реалната практика всичко е по-просто:

Пример 2

Намерете ранга на матрица по метода на индикация на минорите

Решение и отговор в края на урока.

Кога алгоритъмът работи най-бързо? Нека се върнем към същата матрица четири по четири . Очевидно решението ще бъде най-краткото в случай на "добро" ъгъл непълнолетни:

И, ако , тогава , иначе - .

Мисленето изобщо не е хипотетично - има много примери, в които цялото нещо се ограничава само до ъглови малки.

В някои случаи обаче друг метод е по-ефективен и за предпочитане:

Как да намерим ранга на матрица по метода на Гаус?

Този раздел е предназначен за читатели, които вече са запознати Метод на Гауси малко по малко се хванаха за него.

От техническа гледна точка методът не е нов:

1) използвайки елементарни трансформации, привеждаме матрицата в стъпаловидна форма;

2) рангът на матрицата е равен на броя на редовете.

Това е съвсем ясно използването на метода на Гаус не променя ранга на матрицата, а същността тук е изключително проста: според алгоритъма в хода на елементарните трансформации се откриват и отстраняват всички ненужни пропорционални (линейно зависими) линии, в резултат на което остава „сух остатък“ - максималният брой линейно независими линии.

Нека трансформираме старата позната матрица с координатите на три колинеарни вектора:

(1) Първият ред беше добавен към втория ред, умножен по -2. Първият ред беше добавен към третия ред.

(2) Нулевите линии се премахват.

Така че остава един ред, следователно . Излишно е да казвам, че това е много по-бързо, отколкото да се изчислят девет нулеви минор от 2-ри ред и едва след това да се направи заключение.

Напомням ви това само по себе си алгебрична матрицанищо не може да се промени, а трансформациите се извършват само с цел установяване на ранга! Между другото, нека се спрем отново на въпроса, защо не? Матрица на източника 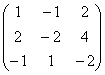носи информация, която е фундаментално различна от информацията за матрица и ред. В някои математически модели (без преувеличение) разликата в едно число може да бъде въпрос на живот и смърт. ... Спомних си училищни учители по математика от начални и средни класове, които безмилостно отрязваха оценката с 1-2 точки за най-малката неточност или отклонение от алгоритъма. И беше страшно разочароващо, когато вместо привидно гарантираната „петица“ се оказа „добро“ или дори по-лошо. Разбирането дойде много по-късно - как иначе да се повери на човек сателити, ядрени бойни глави и електроцентрали? Но не се притеснявайте, аз не работя в тези области =)

Нека да преминем към по-смислени задачи, където между другото ще се запознаем и с важни изчислителни техники Метод на Гаус:

Пример 3

Намерете ранга на матрица с помощта на елементарни трансформации

Решение: дадена матрица четири на пет, което означава, че нейният ранг със сигурност е не повече от 4.

В първата колона няма 1 или -1, следователно са необходими допълнителни стъпки за получаване на поне една единица. През цялото съществуване на сайта многократно ми е задаван въпросът: „Възможно ли е да се пренаредят колоните по време на елементарни трансформации?“. Ето - пренаредена първата или втората колона и всичко е наред! В повечето задачи къде Метод на Гаус, колоните наистина могат да бъдат пренаредени. НО НЕ. И въпросът дори не е възможно объркване с променливи, въпросът е, че в класическия курс на преподаване на висша математика това действие традиционно не се разглежда, следователно, такъв реверанс ще бъде гледан МНОГО криво (или дори принуден да преработи всичко) .

Втората точка се отнася до числата. В процеса на вземане на решение е полезно да се ръководите от следното правило: елементарните трансформации трябва, ако е възможно, да намалят числата на матрицата. В крайна сметка е много по-лесно да се работи с едно-две-три, отколкото например с 23, 45 и 97. И първото действие е насочено не само към получаване на единица в първата колона, но и към елиминиране на номера 7 и 11.

Първо пълното решение, след това коментарите:

(1) Първият ред беше добавен към втория ред, умножен по -2. Първият ред беше добавен към третия ред, умножен по -3. И към купчината: 1-вият ред, умножен по -1, беше добавен към 4-ия ред.

(2) Последните три реда са пропорционални. 3-ти и 4-ти ред бяха изтрити, вторият ред беше преместен на първо място.

(3) Първият ред беше добавен към втория ред, умножен по -3.

Матрицата, намалена до стъпаловидна форма, има два реда.

Отговор:

Сега е ваш ред да измъчвате матрицата четири по четири:

Пример 4

Намерете ранга на матрица по метода на Гаус

напомням ти това Метод на Гаусне предполага недвусмислена твърдост и вашето решение най-вероятно ще бъде различно от моето решение. Кратка извадка от задачата в края на урока.

Какъв метод да използвате за намиране на ранга на матрица?

На практика често изобщо не се казва кой метод трябва да се използва за намиране на ранга. В такава ситуация трябва да се анализира условието - за някои матрици е по-рационално решението да се извърши чрез минорни, докато за други е много по-изгодно да се прилагат елементарни трансформации:

Пример 5

Намерете ранга на матрица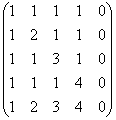

Решение: първият начин някак си веднага изчезва =)

Малко по-високо посъветвах да не докосвате колоните на матрицата, но когато има нулева колона или пропорционални / съвпадащи колони, тогава все пак си струва да ампутирате:

(1) Петата колона е нула, премахваме я от матрицата. По този начин рангът на матрицата е най-много четири. Първият ред се умножава по -1. Това е друга характерна черта на метода на Гаус, която прави следното действие приятна разходка:

(2) Към всички редове, като се започне от втория, е добавен първият ред.

(3) Първият ред беше умножен по -1, третият ред беше разделен на 2, четвъртият ред беше разделен на 3. Вторият ред, умножен по -1, беше добавен към петия ред.

(4) Третият ред беше добавен към петия ред, умножен по -2.

(5) Последните два реда са пропорционални, изтриваме петия.

Резултатът е 4 реда.

Отговор:

Стандартна пететажна сграда за самостоятелно изследване:

Пример 6

Намерете ранга на матрица

Кратко решение и отговор в края на урока.

Трябва да се отбележи, че фразата "матричен ранг" не е толкова често срещана на практика и при повечето проблеми можете да се справите без нея. Но има една задача, при която разглежданата концепция е главният герой и в заключение на статията ще разгледаме това практическо приложение:

Как да изследваме системата от линейни уравнения за съвместимост?

Често в допълнение към решаването системи от линейни уравненияспоред условието първо се изисква да се провери за съвместимост, тоест да се докаже, че изобщо съществува някакво решение. Ключова роля в тази проверка играе Теорема на Кронекер-Капели, който ще формулирам в необходимия вид:

Ако ранг системни матрициравен на ранг разширена матрична система, тогава системата е последователна и ако даденото число съвпада с броя на неизвестните, тогава решението е уникално.

По този начин, за да се проучи системата за съвместимост, е необходимо да се провери равенството , където - системна матрица(запомнете терминологията от урока Метод на Гаус), а - разширена матрична система(т.е. матрица с коефициенти при променливи + колона със свободни термини).

Тази статия ще обсъди такова понятие като ранг на матрица и необходимите допълнителни понятия. Ще дадем примери и доказателства за намиране на ранга на матрица, а също така ще ви кажем какво е матричен минор и защо е толкова важен.

Yandex.RTB R-A-339285-1

Матричен минор

За да разберем какъв е рангът на матрицата, е необходимо да разберем такова понятие като минор на матрицата.

Определение 1

Незначителенкматрица от порядък - детерминантата на квадратна матрица от порядъка k × k, която е съставена от елементите на матрицата A, разположени в предварително избрани k-редове и k-колони, като се запазва позицията на елементите на матрицата A.

Просто казано, ако изтрием (p-k) редове и (n-k) колони в матрица A и направим матрица от тези елементи, които остават, запазвайки подредбата на елементите на матрица A, тогава детерминантата на получената матрица е минор от порядък k на матрица A.

От примера следва, че минорите от първи ред на матрицата A са самите матрични елементи.

Можем да дадем няколко примера за непълнолетни от 2-ри ред. Нека изберем два реда и две колони. Например 1-ви и 2-ри ред, 3-та и 4-та колона.

При този избор на елементи минорът от втори ред ще бъде - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

Друг минор от 2-ри порядък на матрица A е 0 0 1 1 = 0

Нека предоставим илюстрации на конструкцията на минорите от втори ред на матрицата A:

Минорът от 3-ти порядък се получава чрез изтриване на третата колона от матрица A:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

Илюстрация на това как се получава минор от 3-ти порядък на матрица A:

За дадена матрица няма минорни числа по-високи от 3-ти ред, т.к

k ≤ m i n (p , n) = m i n (3, 4) = 3

Колко k-ти порядък минор има за матрица A от порядък p×n?

Броят на непълнолетните се изчислява по следната формула:

C p k × C n k , g e C p k = p ! к! (р - к)! и C nk = n ! к! (n - k) ! - броят на комбинациите от p до k, от n до k, съответно.

След като решим какви са минорите на матрицата A, можем да пристъпим към определяне на ранга на матрицата A.

Матричен ранг: методи за намиране

Определение 2

Матричен ранг - най-високият ред на матрицата, различен от нула.

Обозначение 1

ранг (A), Rg(A), Rang(A).

От дефиницията на ранга на матрица и минор на матрица става ясно, че рангът на нулева матрица е равен на нула, а рангът на ненулева матрица е различен от нула.

Намиране на ранга на матрица по дефиниция

Определение 3

Малък метод на изброяване - метод, базиран на определяне на ранга на матрица.

Алгоритъм на действията чрез изброяване на непълнолетни :

Необходимо е да се намери ранга на матрицата A от порядък стр× н. Ако има поне един ненулев елемент, тогава рангът на матрицата е най-малко равен на единица ( защото е минор от 1-ви ред, който не е равен на нула).

След това следва изброяване на непълнолетните от 2-ри ред. Ако всички минорни от 2-ри ред са равни на нула, тогава рангът е равен на единица. Ако има поне един ненулев минор от 2-ри ред, е необходимо да се премине към изброяването на минорите от 3-ти ред и рангът на матрицата в този случай ще бъде равен на поне две.

Нека направим същото с ранга от 3-ти ред: ако всички минорни числа на матрицата са равни на нула, тогава рангът ще бъде равен на две. Ако има поне един ненулев минор от трети ред, тогава рангът на матрицата е поне три. И така нататък, по аналогия.

Пример 2

Намерете ранга на матрица:

A \u003d - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

Тъй като матрицата не е нула, нейният ранг е най-малко равен на единица.

Минорът от 2-ри ред - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 е различен от нула. Това означава, че рангът на матрицата A е най-малко два.

Подреждаме непълнолетните от 3-ти ред: C 3 3 × C 5 3 = 1 5 ! 3! (5 - 3) ! = 10 бр.

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

Минорите от 3-ти порядък са нула, така че рангът на матрицата е два.

Отговор : Ранг (A) = 2.

Намиране на ранга на матрица по метода на ресни непълнолетни

Определение 3

Малък метод на ресни - метод, който ви позволява да получите резултат с по-малко изчислителна работа.

Ренни минор - минор M o k (k + 1) -ти порядък на матрицата A, който граничи с минорния M от порядък k на матрицата A, ако матрицата, която съответства на минорното M o k "съдържа" матрицата, която съответства на минорната М.

Най-просто казано, матрицата, съответстваща на ограниченото второстепенно M o k, се получава от матрицата, съответстваща на граничното второстепенно M o k, чрез изтриване на елементите на един ред и една колона.

Пример 3

Намерете ранга на матрица:

A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

За да намерим ранга, вземаме минор от 2-ри ред M = 2 - 1 4 1

Записваме всички граничещи непълнолетни:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

За да обосноваме метода на граничещи минорите, представяме теорема, чието формулиране не изисква доказателствена основа.

Теорема 1

Ако всички минори, граничещи с k-тия минор на матрица A от порядък p по n, са равни на нула, тогава всички минорни от порядък (k + 1) на матрица A са равни на нула.

Алгоритъм за действие :

За да намерите ранга на матрица, не е необходимо да преминавате през всички непълнолетни, просто погледнете границите.

Ако граничещите малки са равни на нула, тогава рангът на матрицата е нула. Ако има поне един минор, който не е равен на нула, тогава ние считаме граничещи минор.

Ако всички са нула, тогава ранг(A) е две. Ако има поне един граничещ минор, различен от нула, тогава продължаваме да разглеждаме неговите граничещи минорни. И така нататък, по подобен начин.

Пример 4

Намерете ранга на матрица по метода на индикация на минорите

A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

Как да решим?

Тъй като елементът a 11 от матрицата A не е равен на нула, тогава вземаме минор от 1-ви ред. Нека започнем да търсим граничещ минор, различен от нула:

2 1 4 2 = 2 x 2 - 1 x 4 = 0 2 0 4 1 = 2 x 1 - 0 x 4 = 2

Намерихме граничещ минор от 2-ри ред, който не е равен на нула 2 0 4 1 .

Нека изброим граничещите минори - (има (4 - 2) × (5 - 2) = 6 броя).

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

Отговор : Ранг(A) = 2.

Намиране на ранга на матрица по метода на Гаус (с помощта на елементарни трансформации)

Припомнете си какви са елементарните трансформации.

Елементарни трансформации:

чрез пренареждане на редовете (колони) на матрицата;
чрез умножаване на всички елементи от всеки ред (колона) на матрицата по произволно ненулево число k;

чрез добавяне към елементите на всеки ред (колона) елементи, които съответстват на друг ред (колона) от матрицата, които се умножават по произволно число k.

Определение 5

Намиране на ранга на матрица по метода на Гаус - метод, базиран на теорията за еквивалентността на матриците: ако матрица B е получена от матрица A с помощта на краен брой елементарни трансформации, тогава Rank(A) = Rank(B).

Валидността на това твърдение следва от дефиницията на матрицата:

в случай на пермутация на редове или колони на матрица, нейната детерминанта променя знака. Ако е равно на нула, тогава при пермутиране на редове или колони остава равно на нула;
в случай на умножаване на всички елементи от всеки ред (колона) на матрицата с произволно число k, което не е равно на нула, детерминантата на получената матрица е равна на детерминантата на оригиналната матрица, която се умножава от k;

в случай на добавяне към елементите на определен ред или колона от матрицата съответните елементи от друг ред или колона, които се умножават по числото k, не променя неговия детерминант.

Същността на метода на елементарните трансформации : редуцираме матрицата, чийто ранг се намира, до трапецовидна, използвайки елементарни трансформации.

За какво?

Рангът на матрици от този вид е доста лесен за намиране. Той е равен на броя на редовете, които имат поне един ненулев елемент. И тъй като рангът не се променя по време на елементарни трансформации, това ще бъде рангът на матрицата.

Нека илюстрираме този процес:

за правоъгълни матрици A от порядък p по n, чийто брой редове е по-голям от броя на колоните:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 0 0 0 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 k 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k

за правоъгълни матрици A от порядък p по n, чийто брой редове е по-малък от броя на колоните:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 1 ⋯ b p n , R a n k (A) = p

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 k 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

за квадратни матрици A от порядък n по n:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 0 0 1 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 k 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k ,< n

Пример 5

Намерете ранга на матрица A с помощта на елементарни трансформации:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

Как да решим?

Тъй като елементът a 11 е различен от нула, е необходимо да се умножат елементите от първия ред на матрицата A по 1 a 11 = 1 2:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

Към елементите на 2-ри ред добавяме съответните елементи от 1-ви ред, които се умножават по (-3). Към елементите на 3-ти ред добавяме елементите от 1-ви ред, които се умножават по (-1):

~ A (1) \u003d 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) \u003d \u003d 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5 ) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

Елементът a 22 (2) е различен от нула, така че умножаваме елементите на 2-рия ред на матрицата A по A (2) по a 1 a 22 (2) = - 2 3:

A (3) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

Към елементите от 3-тия ред на получената матрица добавяме съответните елементи от 2-рия ред, които се умножават по 3 2 ;
към елементите от 4-ти ред - елементите от 2-ри ред, които се умножават по 9 2 ;
към елементите на 5-ти ред - елементите от 2-ри ред, които се умножават по 3 2 .

Всички елементи на реда са нула. Така с помощта на елементарни трансформации сме свели матрицата до трапецовидна форма, от която се вижда, че R a n k (A (4)) = 2 . От това следва, че рангът на оригиналната матрица също е равен на две.

Коментирайте

Ако извършвате елементарни трансформации, тогава приблизителни стойности не са разрешени!

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

Нека бъде дадена някаква матрица:

Изберете в тази матрица произволни линии и произволни колони
. Тогава детерминантата порядък, съставен от матрични елементи
разположен в пресечната точка на избрани редове и колони се нарича второстепенен -тия ред матрица
.

Определение 1.13.Матричен ранг
е най-големият ред на ненулевия минор на тази матрица.

За да се изчисли ранга на матрица, трябва да се вземат предвид всички нейни минорни от най-малкия ред и, ако поне един от тях е различен от нула, да се премине към разглеждането на минорите от най-висок ред. Този подход за определяне на ранга на матрица се нарича граничния метод (или метода на граничните малки).

Задача 1.4.По метода на обграждане на непълнолетни определете ранга на матрица
.

Помислете за граничене от първи ред, например,
. След това преминаваме към разглеждането на някаква граница от втори ред.

Например,
.

И накрая, нека анализираме границата на третия ред.

Така че най-високият ред на ненулев минор е 2, следователно
.

При решаване на задача 1.4 може да се забележи, че поредицата от граничещи минори от втори ред са различни от нула. В тази връзка възниква следната представа.

Определение 1.14.Базисният минор на матрицата е всеки ненулев минор, чийто ред е равен на ранга на матрицата.

Теорема 1.2.(Основна минорна теорема). Основните редове (основните колони) са линейно независими.

Забележете, че редовете (колоните) на матрицата са линейно зависими, ако и само ако поне един от тях може да бъде представен като линейна комбинация от останалите.

Теорема 1.3.Броят на линейно независимите матрични редове е равен на броя на линейно независимите матрични колони и е равен на ранга на матрицата.

Теорема 1.4.(Необходимо и достатъчно условие детерминантата да е равна на нула). За да се определи детерминанта -та поръчка е равно на нула, е необходимо и достатъчно неговите редове (колони) да бъдат линейно зависими.

Изчисляването на ранга на матрица въз основа на нейната дефиниция е твърде тромаво. Това става особено важно за матрици от висок порядък. В тази връзка на практика рангът на матрица се изчислява въз основа на прилагането на теореми 10.2 - 10.4, както и използването на концепциите за еквивалентност на матрицата и елементарни трансформации.

Определение 1.15.Две матрици
и се наричат еквивалентни, ако ранговете им са равни, т.е.
.

Ако матрици
и са еквивалентни, тогава забележете
 .

Теорема 1.5.Рангът на матрица не се променя от елементарни трансформации.

Ще наречем елементарни трансформации на матрицата
някое от следните действия върху матрицата:

Замяна на редове с колони и колони със съответни редове;

Пермутация на матрични редове;

Зачеркване на линия, всички елементи на която са равни на нула;

Умножаване на произволен низ по число, различно от нула;

Добавяне към елементите на един ред на съответните елементи от друг ред, умножени по същото число
.

Следствие от теорема 1.5.Ако матрицата
получени от матрицата използвайки краен брой елементарни трансформации, след това матриците
и са еквивалентни.

При изчисляване на ранга на матрица, тя трябва да бъде намалена до трапецовидна форма, като се използва краен брой елементарни трансформации.

Определение 1.16.Ще наречем трапец такава форма на представяне на матрица, когато в граничния минор от най-големия ненулев ред всички елементи под диагоналните изчезват. Например:

Тук
, матрични елементи
обърнете на нула. Тогава формата на представяне на такава матрица ще бъде трапецовидна.

Като правило матриците се редуцират до трапецовидна форма с помощта на алгоритъма на Гаус. Идеята на алгоритъма на Гаус е, че чрез умножаване на елементите от първия ред на матрицата по съответните фактори се постига, че всички елементи от първата колона се намират под елемента
, ще се превърне в нула. След това, умножавайки елементите на втората колона по съответните множители, постигаме, че всички елементи от втората колона се намират под елемента
, ще се превърне в нула. По-нататък продължете по същия начин.