লগারিদমিক অসমতা সম্পর্কে সব। উদাহরণ বিশ্লেষণ। জটিল লগারিদমিক অসমতা একটি পরিবর্তনশীল সহ লগারিদমিক অসমতা

আপনি কি মনে করেন যে পরীক্ষার আগে এখনও সময় আছে, এবং আপনি প্রস্তুতির জন্য সময় পাবেন? সম্ভবত এই তাই. তবে যাই হোক না কেন, ছাত্র যত আগে প্রশিক্ষণ শুরু করে, তত বেশি সফলতার সাথে সে পরীক্ষায় উত্তীর্ণ হয়। আজ আমরা লগারিদমিক অসমতার জন্য একটি নিবন্ধ উৎসর্গ করার সিদ্ধান্ত নিয়েছি। এটি একটি কাজ, যার অর্থ একটি অতিরিক্ত পয়েন্ট পাওয়ার সুযোগ।

আপনি কি ইতিমধ্যে একটি লগারিদম (লগ) কি জানেন? আমরা সত্যিই তাই আশা. তবে আপনার কাছে এই প্রশ্নের উত্তর না থাকলেও সমস্যা নেই। লগারিদম কি তা বোঝা খুব সহজ।

কেন ঠিক 4? 81 পাওয়ার জন্য আপনাকে 3 নম্বরটিকে এমন একটি শক্তিতে বাড়াতে হবে। আপনি যখন নীতিটি বুঝতে পারবেন, আপনি আরও জটিল গণনায় এগিয়ে যেতে পারেন।

আপনি কয়েক বছর আগে অসমতার মধ্য দিয়ে গেছেন। এবং তারপর থেকে, আপনি ক্রমাগত গণিতে তাদের সাথে দেখা করেন। আপনার যদি অসমতা সমাধান করতে সমস্যা হয় তবে উপযুক্ত বিভাগটি দেখুন।
এখন, যখন আমরা আলাদাভাবে ধারণাগুলির সাথে পরিচিত হয়েছি, তখন আমরা সাধারণভাবে তাদের বিবেচনায় চলে যাব।

সহজ লগারিদমিক অসমতা।

সহজ লগারিদমিক অসমতা এই উদাহরণের মধ্যে সীমাবদ্ধ নয়, আরও তিনটি আছে, শুধুমাত্র বিভিন্ন চিহ্ন সহ। কেন এই প্রয়োজন? লগারিদম দিয়ে অসমতা কিভাবে সমাধান করা যায় তা আরও ভালোভাবে বুঝতে। এখন আমরা একটি আরও প্রযোজ্য উদাহরণ দিই, এখনও বেশ সহজ, আমরা জটিল লগারিদমিক অসমতাগুলিকে পরে রেখে দিই।

এটা কিভাবে সমাধান করতে? এটি সব ODZ দিয়ে শুরু হয়। আপনি যদি সর্বদা সহজে কোনো অসমতা সমাধান করতে চান তবে আপনার এটি সম্পর্কে আরও জানা উচিত।

ODZ কি? লগারিদমিক অসমতার জন্য DPV

সংক্ষিপ্ত রূপটি বৈধ মানের পরিসীমাকে বোঝায়। পরীক্ষার জন্য অ্যাসাইনমেন্টে, এই শব্দটি প্রায়ই পপ আপ হয়। DPV শুধুমাত্র লগারিদমিক অসমতার ক্ষেত্রেই আপনার জন্য উপযোগী নয়।

উপরের উদাহরণটি আবার দেখুন। আমরা এটির উপর ভিত্তি করে ODZ বিবেচনা করব, যাতে আপনি নীতিটি বুঝতে পারেন এবং লগারিদমিক অসমতার সমাধান প্রশ্ন উত্থাপন না করে। লগারিদমের সংজ্ঞা থেকে এটি অনুসরণ করে যে 2x+4 অবশ্যই শূন্যের চেয়ে বড় হতে হবে। আমাদের ক্ষেত্রে, এর মানে নিম্নলিখিত।

এই সংখ্যা সংজ্ঞা দ্বারা ইতিবাচক হতে হবে. উপরে উপস্থাপিত অসমতা সমাধান করুন। এটি মৌখিকভাবেও করা যেতে পারে, এখানে এটা স্পষ্ট যে X 2 এর কম হতে পারে না। অসমতার সমাধান হবে গ্রহণযোগ্য মানগুলির পরিসরের সংজ্ঞা।
এখন সরল লগারিদমিক অসমতা সমাধানের দিকে এগিয়ে যাওয়া যাক।

আমরা অসমতার উভয় অংশ থেকে লগারিদমগুলিকে বাতিল করি। এর ফলে আমাদের জন্য কি অবশিষ্ট আছে? সহজ অসমতা।

এটা সমাধান করা সহজ. X -0.5 এর বেশি হতে হবে। এখন আমরা দুটি প্রাপ্ত মান সিস্টেমে একত্রিত করি। এইভাবে,

এটি বিবেচিত লগারিদমিক অসমতার জন্য গ্রহণযোগ্য মানের অঞ্চল হবে।

কেন ODZ আদৌ প্রয়োজন? এটি ভুল এবং অসম্ভব উত্তরগুলি আগাছা করার একটি সুযোগ। যদি উত্তরটি গ্রহণযোগ্য মানের সীমার মধ্যে না হয়, তাহলে উত্তরটি সহজভাবে বোঝা যায় না। এটি দীর্ঘ সময়ের জন্য মনে রাখার মতো, যেহেতু পরীক্ষায় প্রায়শই ODZ অনুসন্ধান করার প্রয়োজন হয় এবং এটি কেবল লগারিদমিক বৈষম্যই নয়।

লগারিদমিক অসমতা সমাধানের জন্য অ্যালগরিদম

সমাধানটি বেশ কয়েকটি ধাপ নিয়ে গঠিত। প্রথমত, গ্রহণযোগ্য মানের পরিসীমা খুঁজে বের করা প্রয়োজন। ODZ-এ দুটি মান থাকবে, আমরা এটি উপরে বিবেচনা করেছি। পরবর্তী পদক্ষেপটি হল বৈষম্য নিজেই সমাধান করা। সমাধান পদ্ধতি নিম্নরূপ:

• গুণক প্রতিস্থাপন পদ্ধতি;
• পচন
• যৌক্তিককরণ পদ্ধতি।

পরিস্থিতির উপর নির্ভর করে, উপরের পদ্ধতিগুলির মধ্যে একটি ব্যবহার করা উচিত। চলুন সরাসরি সমাধানে যাওয়া যাক। আমরা সবচেয়ে জনপ্রিয় পদ্ধতিটি প্রকাশ করব যা প্রায় সব ক্ষেত্রেই USE কাজগুলি সমাধান করার জন্য উপযুক্ত। এর পরে, আমরা পচন পদ্ধতি বিবেচনা করব। আপনি যদি একটি বিশেষভাবে "কঠিন" অসমতার সম্মুখীন হন তবে এটি সাহায্য করতে পারে। সুতরাং, লগারিদমিক অসমতা সমাধানের জন্য অ্যালগরিদম।

সমাধান উদাহরণ :

এটা বৃথা নয় যে আমরা অবিকল যেমন একটি অসমতা গ্রহণ! বেস মনোযোগ দিন। মনে রাখবেন: যদি এটি একের বেশি হয়, বৈধ মানের পরিসীমা খুঁজে বের করার সময় চিহ্নটি একই থাকে; অন্যথায়, বৈষম্য চিহ্ন পরিবর্তন করা আবশ্যক।

ফলস্বরূপ, আমরা অসমতা পাই:

এখন আমরা বাম দিকটিকে শূন্যের সমান সমীকরণের আকারে নিয়ে আসি। "কম" চিহ্নের পরিবর্তে, আমরা "সমান" রাখি, আমরা সমীকরণটি সমাধান করি। এইভাবে, আমরা ODZ খুঁজে পাব। আমরা আশা করি যে এই ধরনের একটি সহজ সমীকরণ সমাধান করতে আপনার কোন সমস্যা হবে না। উত্তরগুলি হল -4 এবং -2। এটাই সবকিছু না. আপনাকে চার্টে এই পয়েন্টগুলি প্রদর্শন করতে হবে, "+" এবং "-" রাখুন। এই জন্য কি করা প্রয়োজন? রাশিতে ব্যবধান থেকে সংখ্যা প্রতিস্থাপন করুন। যেখানে মানগুলি ইতিবাচক, আমরা সেখানে "+" রাখি।

উত্তর: x -4-এর বেশি এবং -2-এর কম হতে পারে না।

আমরা শুধুমাত্র বাম দিকের জন্য বৈধ মানের পরিসীমা খুঁজে পেয়েছি, এখন আমাদের ডান পাশের জন্য বৈধ মানের পরিসীমা খুঁজে বের করতে হবে। এটা কোনোভাবেই সহজ নয়। উত্তর:-2। আমরা উভয় প্রাপ্ত এলাকা ছেদ.

এবং শুধুমাত্র এখন আমরা বৈষম্য নিজেই সমাধান করতে শুরু করি।

সিদ্ধান্ত নেওয়া সহজ করার জন্য এটি যতটা সম্ভব সহজ করা যাক।

আমরা আবার সমাধানে ব্যবধান পদ্ধতি ব্যবহার করি। আসুন গণনাগুলি এড়িয়ে যাই, তার সাথে আগের উদাহরণ থেকে সবকিছু ইতিমধ্যে পরিষ্কার। উত্তর.

কিন্তু লগারিদমিক অসমতার একই ভিত্তি থাকলে এই পদ্ধতিটি উপযুক্ত।

লগারিদমিক সমীকরণ এবং বিভিন্ন বেসের সাথে অসমতা সমাধান করার জন্য একটি বেসে প্রাথমিক হ্রাস জড়িত। তারপর উপরের পদ্ধতিটি ব্যবহার করুন। তবে আরও জটিল মামলা রয়েছে। লগারিদমিক অসমতার সবচেয়ে জটিল প্রকারের একটি বিবেচনা করুন।

পরিবর্তনশীল ভিত্তি সহ লগারিদমিক অসমতা

কিভাবে এই ধরনের বৈশিষ্ট্য সঙ্গে অসমতা সমাধান? হ্যাঁ, এবং এই ধরনের পরীক্ষা পাওয়া যাবে. নিম্নলিখিত উপায়ে বৈষম্য সমাধান করা আপনার শিক্ষাগত প্রক্রিয়াতেও উপকারী প্রভাব ফেলবে। আসুন বিস্তারিতভাবে সমস্যা তাকান. আসুন তত্ত্বকে একপাশে রেখে সরাসরি অনুশীলনে যাই। লগারিদমিক অসমতা সমাধানের জন্য, একবার উদাহরণের সাথে নিজেকে পরিচিত করা যথেষ্ট।

উপস্থাপিত ফর্মের লগারিদমিক অসমতা সমাধানের জন্য, একই বেস সহ লগারিদমের ডান দিকটি আনতে হবে। নীতিটি সমতুল্য রূপান্তরের অনুরূপ। ফলে বৈষম্য এরকম দেখাবে।

প্রকৃতপক্ষে, লগারিদম ছাড়াই অসমতার একটি সিস্টেম তৈরি করা বাকি আছে। যৌক্তিককরণ পদ্ধতি ব্যবহার করে, আমরা বৈষম্যের সমতুল্য ব্যবস্থায় চলে যাই। আপনি যখন উপযুক্ত মানগুলি প্রতিস্থাপন করবেন এবং তাদের পরিবর্তনগুলি অনুসরণ করবেন তখন আপনি নিজেই নিয়মটি বুঝতে পারবেন। সিস্টেমে নিম্নলিখিত অসমতা থাকবে।

যৌক্তিককরণ পদ্ধতি ব্যবহার করে, অসমতাগুলি সমাধান করার সময়, আপনাকে নিম্নলিখিতগুলি মনে রাখতে হবে: আপনাকে বেস থেকে একটি বিয়োগ করতে হবে, লগারিদমের সংজ্ঞা অনুসারে x, অসমতার উভয় অংশ থেকে বিয়োগ করা হয় (বাম থেকে ডান), দুটি অভিব্যক্তি গুণিত হয় এবং শূন্যের সাথে সম্পর্কিত মূল চিহ্নের নীচে সেট করা হয়।

আরও সমাধান ব্যবধান পদ্ধতি দ্বারা বাহিত হয়, এখানে সবকিছু সহজ। সমাধান পদ্ধতির পার্থক্য বোঝা আপনার জন্য গুরুত্বপূর্ণ, তারপর সবকিছু সহজে কাজ করতে শুরু করবে।

লগারিদমিক অসমতার মধ্যে অনেক সূক্ষ্মতা রয়েছে। তাদের মধ্যে সবচেয়ে সহজ সমাধান করা যথেষ্ট সহজ। সমস্যা ছাড়াই তাদের প্রতিটি সমাধান করার জন্য এটি কীভাবে তৈরি করবেন? আপনি ইতিমধ্যে এই নিবন্ধে সব উত্তর পেয়েছেন. এখন আপনার সামনে দীর্ঘ অনুশীলন রয়েছে। ক্রমাগত পরীক্ষার মধ্যে বিভিন্ন সমস্যা সমাধানের অনুশীলন করুন এবং আপনি সর্বোচ্চ স্কোর পেতে সক্ষম হবেন। আপনার কঠিন কাজ সৌভাগ্য!

লগারিদমিক বৈষম্যের সম্পূর্ণ বৈচিত্র্যের মধ্যে, একটি পরিবর্তনশীল ভিত্তি সহ অসমতাগুলি আলাদাভাবে অধ্যয়ন করা হয়। এগুলি একটি বিশেষ সূত্র অনুসারে সমাধান করা হয়, যা কিছু কারণে স্কুলে খুব কমই শেখানো হয়। উপস্থাপনাটি গণিতে C3 USE - 2014 টাস্কের সমাধান উপস্থাপন করে।

ডাউনলোড করুন:

পূর্বরূপ:

উপস্থাপনাগুলির পূর্বরূপ ব্যবহার করতে, একটি Google অ্যাকাউন্ট (অ্যাকাউন্ট) তৈরি করুন এবং সাইন ইন করুন: https://accounts.google.com

স্লাইড ক্যাপশন:

লগারিদমের ভিত্তিতে একটি পরিবর্তনশীল সমন্বিত লগারিদমিক অসমতা সমাধান করা: পদ্ধতি, কৌশল, গণিতের MBOU মাধ্যমিক বিদ্যালয় নং 143 Knyazkina T.V. এর সমতুল্য রূপান্তর শিক্ষক।

লগারিদমিক বৈষম্যের সম্পূর্ণ বৈচিত্র্যের মধ্যে, একটি পরিবর্তনশীল ভিত্তি সহ অসমতাগুলি আলাদাভাবে অধ্যয়ন করা হয়। এগুলি একটি বিশেষ সূত্র ব্যবহার করে সমাধান করা হয়, যা কিছু কারণে স্কুলে খুব কমই পড়ানো হয়: লগ k (x) f (x) ∨ লগ k (x) g (x) ⇒ (f (x) − g (x)) ( k ( x) − 1) ∨ 0 "∨" চেকবক্সের পরিবর্তে, আপনি যেকোনো অসমতার চিহ্ন রাখতে পারেন: কম বা বেশি। প্রধান বিষয় হল যে উভয় অসমতার লক্ষণগুলি একই। তাই আমরা লগারিদম থেকে পরিত্রাণ পেতে পারি এবং সমস্যাটিকে একটি যৌক্তিক অসমতায় কমিয়ে দিই। পরেরটি সমাধান করা অনেক সহজ, কিন্তু লগারিদম বর্জন করার সময়, অতিরিক্ত শিকড় উপস্থিত হতে পারে। তাদের কেটে ফেলার জন্য, এটি গ্রহণযোগ্য মানগুলির পরিসীমা খুঁজে বের করার জন্য যথেষ্ট। লগারিদমের ODZ ভুলে যাবেন না! গ্রহণযোগ্য মানগুলির পরিসরের সাথে সম্পর্কিত সমস্ত কিছু লিখতে হবে এবং আলাদাভাবে সমাধান করতে হবে: f (x) > 0; g(x) > 0; k(x) > 0; k (x) ≠ 1. এই চারটি অসমতা একটি সিস্টেম গঠন করে এবং একই সাথে পূরণ করতে হবে। যখন গ্রহণযোগ্য মানগুলির পরিসীমা পাওয়া যায়, তখন এটি একটি যুক্তিযুক্ত অসমতার সমাধানের সাথে এটি অতিক্রম করতে থাকে - এবং উত্তর প্রস্তুত।

অসমতা সমাধান করুন: সমাধান শুরু করার জন্য, আসুন লগারিদমের ODZ লিখি। প্রথম দুটি অসমতা স্বয়ংক্রিয়ভাবে সঞ্চালিত হয়, এবং শেষটি রং করতে হবে। যেহেতু একটি সংখ্যার বর্গ শূন্যের সমান যদি এবং শুধুমাত্র যদি সংখ্যাটি শূন্যের সমান হয়, তাহলে আমাদের আছে: x 2 + 1 ≠ 1; x2 ≠ 0; x ≠ 0। দেখা যাচ্ছে যে লগারিদমের ODZ হল শূন্য বাদে সমস্ত সংখ্যা: x ∈ (−∞0)∪(0 ;+ ∞)। এখন আমরা মূল অসমতার সমাধান করি: আমরা লগারিদমিক অসমতা থেকে যৌক্তিক একটিতে রূপান্তর করি। মূল অসমতার মধ্যে একটি "কম" চিহ্ন রয়েছে, তাই এর ফলে অসমতা একটি "এর চেয়ে কম" চিহ্নের সাথে হওয়া উচিত।

আমাদের আছে: (10 − (x 2 + 1)) (x 2 + 1 −1)

লগারিদমিক অসমতা রূপান্তর করা প্রায়শই মূল অসমতা উপরের একটি থেকে পৃথক হয়। লগারিদমের সাথে কাজ করার জন্য আদর্শ নিয়মগুলি ব্যবহার করে এটি ঠিক করা সহজ। যথা: যেকোন সংখ্যাকে একটি প্রদত্ত বেস সহ লগারিদম হিসাবে উপস্থাপন করা যেতে পারে; একই বেস সহ লগারিদমের যোগফল এবং পার্থক্য একটি একক লগারিদম দ্বারা প্রতিস্থাপিত হতে পারে। আলাদাভাবে, আমি আপনাকে গ্রহণযোগ্য মানগুলির পরিসর সম্পর্কে মনে করিয়ে দিতে চাই। যেহেতু মূল অসমতার মধ্যে বেশ কয়েকটি লগারিদম থাকতে পারে, তাই তাদের প্রতিটির DPV খুঁজে বের করতে হবে। এইভাবে, লগারিদমিক অসমতা সমাধানের জন্য সাধারণ স্কিমটি নিম্নরূপ: অসমতার অন্তর্ভুক্ত প্রতিটি লগারিদমের জন্য ODZ খুঁজুন; লগারিদম যোগ এবং বিয়োগ করার সূত্র ব্যবহার করে মানকটিতে অসমতা হ্রাস করুন; উপরের স্কিম অনুযায়ী ফলস্বরূপ অসমতা সমাধান করুন।

অসমতা সমাধান করুন: সমাধান আসুন প্রথম লগারিদমের ডোমেইন অফ ডেফিনিশন (ODZ) সন্ধান করি: আমরা ব্যবধানের পদ্ধতি দ্বারা সমাধান করি। লবটির শূন্য বের কর: 3 x − 2 = 0; x = 2/3। তারপর - হর শূন্য: x − 1 = 0; x = 1. আমরা স্থানাঙ্ক লাইনে শূন্য এবং চিহ্নগুলি চিহ্নিত করি:

আমরা x ∈ (−∞ 2/3) ∪ (1; +∞) পাই। ODZ এর দ্বিতীয় লগারিদম একই হবে। আপনি আমাকে বিশ্বাস না হলে, আপনি চেক করতে পারেন. এখন দ্বিতীয় লগারিদমকে রূপান্তর করা যাক যাতে বেসে দুটি থাকে: আপনি দেখতে পাচ্ছেন, বেস এবং লগারিদমের সামনে ট্রিপলগুলি হ্রাস করা হয়েছে। একই বেস সহ দুটি লগারিদম পান। তাদের যোগ করুন: লগ 2 (x − 1) 2

(f (x) − g (x)) (k (x) − 1)

আমরা সেটগুলির ছেদ করতে আগ্রহী, তাই আমরা উভয় তীরের ছায়াযুক্ত বিরতিগুলি বেছে নিই। আমরা পাই: x ∈ (−1; 2/3) ∪ (1; 3) - সমস্ত বিন্দু পাংচার করা হয়েছে। উত্তর: x ∈ (−1; 2/3)∪(1; 3)

ইউনিফাইড স্টেট পরীক্ষা-2014 টাইপ C3 এর কাজগুলি সমাধান করা

বৈষম্য ব্যবস্থার সমাধান করুন। ODZ:  1) 2)

অসমতার পদ্ধতিটি সমাধান করুন 3) -7 -3 - 5 x -1 + + + − − (চলবে)

অসমতার ব্যবস্থা সমাধান করুন 4) সাধারণ সমাধান: এবং -7 -3 - 5 x -1 -8 7 লগ 2 129 (চলবে)

অসমতা সমাধান করুন (চলবে) -3 3 -1 + - + - x 17 + -3 3 -1 x 17 -4

অসমতার সমাধান করুন। ODZ: 

অসমতা সমাধান করুন (চলবে)

অসমতার সমাধান করুন। ODZ:  -2 1 -1 + - + - x + 2 -2 1 -1 x 2

ব্যবহারে লগারিদমিক অসাম্য

সেচিন মিখাইল আলেকজান্দ্রোভিচ

কাজাখস্তান প্রজাতন্ত্রের ছাত্রদের জন্য ছোট একাডেমি অফ সায়েন্সেস "অনুসন্ধানী"

MBOU "সোভিয়েত মাধ্যমিক বিদ্যালয় নং 1", গ্রেড 11, শহর। সোভিয়েতস্কি সোভিয়েত জেলা

গুঙ্কো লিউডমিলা দিমিত্রিভনা, এমবিইউ এর শিক্ষক "সোভিয়েত মাধ্যমিক বিদ্যালয় নং 1"

সোভিয়েতস্কি জেলা

উদ্দেশ্য:অ-মানক পদ্ধতি ব্যবহার করে C3 লগারিদমিক অসমতা সমাধানের পদ্ধতির অধ্যয়ন, লগারিদম সম্পর্কে আকর্ষণীয় তথ্য প্রকাশ করে।

পাঠ্য বিষয়:

3) অ-মানক পদ্ধতি ব্যবহার করে নির্দিষ্ট লগারিদমিক C3 অসমতা সমাধান করতে শিখুন।

ফলাফল:

বিষয়বস্তু

ভূমিকা ……………………………………………………………………………….৪

অধ্যায় 1। পটভূমি……………………………………………………………….৫

অধ্যায় 2. লগারিদমিক অসমতার সংগ্রহ ……………………… 7

2.1। সমতুল্য রূপান্তর এবং ব্যবধানের সাধারণীকৃত পদ্ধতি…………… 7

2.2। যৌক্তিককরণ পদ্ধতি ………………………………………………… 15

2.3। অ-মানক প্রতিস্থাপন ……………………………………………………………………………………………………… ..... 22

2.4। ফাঁদ সহ কাজ……………………………………………………… ২৭

উপসংহার……………………………………………………………… 30

সাহিত্য………………………………………………………………. 31

ভূমিকা

আমি 11 তম শ্রেণীতে আছি এবং আমি এমন একটি বিশ্ববিদ্যালয়ে প্রবেশ করার পরিকল্পনা করছি যেখানে গণিত একটি মূল বিষয়। এই কারণেই আমি অংশ C এর কাজগুলির সাথে অনেক কাজ করি। টাস্ক C3-তে, আপনাকে একটি অ-মানক অসমতা বা অসমতার একটি সিস্টেম সমাধান করতে হবে, সাধারণত লগারিদমের সাথে যুক্ত। পরীক্ষার জন্য প্রস্তুতি নেওয়ার সময়, আমি C3 তে দেওয়া পরীক্ষার লগারিদমিক অসমতা সমাধানের পদ্ধতি এবং কৌশলগুলির অভাবের সমস্যার সম্মুখীন হয়েছিলাম। এই বিষয়ে স্কুল পাঠ্যক্রমে যে পদ্ধতিগুলি অধ্যয়ন করা হয় তা C3 সমাধানের জন্য একটি ভিত্তি প্রদান করে না। গণিতের শিক্ষক পরামর্শ দিয়েছিলেন যে আমি তার নির্দেশনায় আমার নিজের উপর C3 অ্যাসাইনমেন্ট নিয়ে কাজ করি। উপরন্তু, আমি প্রশ্নে আগ্রহী ছিল: আমাদের জীবনে লগারিদম আছে?

এটি মাথায় রেখে, থিমটি বেছে নেওয়া হয়েছিল:

"পরীক্ষায় লগারিদমিক অসমতা"

উদ্দেশ্য:লগারিদম সম্পর্কে আকর্ষণীয় তথ্য প্রকাশ করে অ-মানক পদ্ধতি ব্যবহার করে C3 সমস্যা সমাধানের প্রক্রিয়ার অধ্যয়ন।

পাঠ্য বিষয়:

1) লগারিদমিক অসমতা সমাধানের জন্য অ-মানক পদ্ধতি সম্পর্কে প্রয়োজনীয় তথ্য খুঁজুন।

2) লগারিদম সম্পর্কে অতিরিক্ত তথ্য খুঁজুন।

3) অ-মানক পদ্ধতি ব্যবহার করে নির্দিষ্ট C3 সমস্যা সমাধান করতে শিখুন।

ফলাফল:

ব্যবহারিক তাত্পর্য C3 সমস্যা সমাধানের জন্য যন্ত্রপাতি সম্প্রসারণের মধ্যে নিহিত। এই উপাদানটি কিছু পাঠে ব্যবহার করা যেতে পারে, বৃত্ত পরিচালনার জন্য, গণিতের ঐচ্ছিক ক্লাস।

প্রকল্পের পণ্যটি হবে "সমাধান সহ লগারিদমিক C3 অসমতা" সংগ্রহ।

অধ্যায় 1। পটভূমি

16শ শতাব্দীতে, প্রাথমিকভাবে জ্যোতির্বিদ্যায় আনুমানিক গণনার সংখ্যা দ্রুত বৃদ্ধি পায়। যন্ত্রের উন্নতি, গ্রহের গতিবিধির অধ্যয়ন এবং অন্যান্য কাজের জন্য প্রচুর পরিমাণে, কখনও কখনও অনেক বছর, গণনার প্রয়োজন হয়। জ্যোতির্বিদ্যা অসম্পূর্ণ গণনায় ডুবে যাওয়ার সত্যিকারের বিপদে ছিল। অন্যান্য ক্ষেত্রেও অসুবিধা দেখা দেয়, উদাহরণস্বরূপ, বীমা ব্যবসায়, বিভিন্ন শতাংশ মানের জন্য চক্রবৃদ্ধি সুদের টেবিলের প্রয়োজন ছিল। প্রধান অসুবিধা ছিল গুণন, বহু-সংখ্যার বিভাজন, বিশেষ করে ত্রিকোণমিতিক পরিমাণ।

লগারিদমের আবিষ্কারটি 16 শতকের শেষের দিকে অগ্রগতির সুপরিচিত বৈশিষ্ট্যের উপর ভিত্তি করে করা হয়েছিল। আর্কিমিডিস জ্যামিতিক অগ্রগতি q, q2, q3, ... এবং তাদের সূচক 1, 2, 3, ... এর গাণিতিক অগ্রগতির সদস্যদের মধ্যে সংযোগ সম্পর্কে কথা বলেছেন সামাইটে। আর একটি পূর্বশর্ত ছিল ডিগ্রী ধারণাকে ঋণাত্মক এবং ভগ্নাংশের সূচকে প্রসারিত করা। অনেক লেখক উল্লেখ করেছেন যে গুণ, ভাগ, একটি শক্তিতে উত্থাপন এবং একটি মূল নিষ্কাশন সূচকীয়ভাবে পাটিগণিতের সাথে মিলে যায় - একই ক্রমে - যোগ, বিয়োগ, গুণ এবং ভাগ।

এখানে একটি সূচক হিসাবে লগারিদমের ধারণা ছিল।

লগারিদমের মতবাদের বিকাশের ইতিহাসে, বেশ কয়েকটি পর্যায় অতিক্রম করেছে।

ধাপ 1

লগারিদম 1594 সালের পরে স্বাধীনভাবে স্কটিশ ব্যারন নেপিয়ার (1550-1617) দ্বারা এবং দশ বছর পরে সুইস মেকানিক বুর্গি (1552-1632) দ্বারা আবিষ্কৃত হয়েছিল। উভয়ই পাটিগণিত গণনার একটি নতুন সুবিধাজনক উপায় প্রদান করতে চেয়েছিল, যদিও তারা বিভিন্ন উপায়ে এই সমস্যাটির সাথে যোগাযোগ করেছিল। নেপিয়ার গতিশীলভাবে লগারিদমিক ফাংশন প্রকাশ করেন এবং এইভাবে ফাংশন তত্ত্বের একটি নতুন ক্ষেত্রে প্রবেশ করেন। Bürgi বিচ্ছিন্ন অগ্রগতি বিবেচনার ভিত্তিতে রয়ে গেছে. যাইহোক, উভয়ের জন্য লগারিদমের সংজ্ঞা আধুনিক একের মত নয়। "লগারিদম" (লগারিদমাস) শব্দটি নেপিয়ারের অন্তর্গত। এটি গ্রীক শব্দের সংমিশ্রণ থেকে উদ্ভূত হয়েছে: লোগো - "সম্পর্ক" এবং আরিকমো - "সংখ্যা", যার অর্থ "সম্পর্কের সংখ্যা"। প্রাথমিকভাবে, নেপিয়ার একটি ভিন্ন পরিভাষা ব্যবহার করেছিলেন: সংখ্যার কৃত্রিম - "কৃত্রিম সংখ্যা", সংখ্যাগত প্রাকৃতিকতার বিপরীতে - "প্রাকৃতিক সংখ্যা"।

1615 সালে, লন্ডনের গ্রেশ কলেজের গণিতের অধ্যাপক হেনরি ব্রিগস (1561-1631) এর সাথে একটি কথোপকথনে, নেপিয়ার একটির লগারিদমের জন্য শূন্য এবং দশটির লগারিদমের জন্য 100 নেওয়ার পরামর্শ দিয়েছিলেন, বা, কী পরিমাণ সমান। , মাত্র 1. এইভাবে দশমিক লগারিদম এবং প্রথম লগারিদমিক টেবিল মুদ্রিত হয়েছিল। পরবর্তীতে, ডাচ বই বিক্রেতা এবং গণিতবিদ আন্দ্রিয়ান ফ্লাক (1600-1667) দ্বারা ব্রিগস টেবিলের পরিপূরক হয়। নেপিয়ার এবং ব্রিগস, যদিও তারা অন্য কারো আগে লগারিদমে এসেছিলেন, তাদের টেবিল অন্যদের তুলনায় পরে প্রকাশ করেছিলেন - 1620 সালে। 1624 সালে আই. কেপলার দ্বারা চিহ্ন লগ এবং লগ প্রবর্তন করা হয়। "প্রাকৃতিক লগারিদম" শব্দটি 1659 সালে মেঙ্গোলি দ্বারা প্রবর্তিত হয়, 1668 সালে এন. মার্কেটর অনুসরণ করেন এবং লন্ডনের শিক্ষক জন স্প্যাডেল "নতুন লগারিদম" নামে 1 থেকে 1000 পর্যন্ত সংখ্যার প্রাকৃতিক লগারিদমের সারণী প্রকাশ করেন।

রাশিয়ান ভাষায়, প্রথম লগারিদমিক টেবিল 1703 সালে প্রকাশিত হয়েছিল। কিন্তু সমস্ত লগারিদমিক সারণীতে, গণনায় ভুল করা হয়েছিল। জার্মান গণিতবিদ কে. ব্রেমিকার (1804-1877) এর প্রক্রিয়াকরণে 1857 সালে বার্লিনে প্রথম ত্রুটি-মুক্ত টেবিল প্রকাশিত হয়েছিল।

ধাপ ২

লগারিদম তত্ত্বের আরও উন্নয়ন বিশ্লেষণাত্মক জ্যামিতি এবং অসীম ক্যালকুলাসের বিস্তৃত প্রয়োগের সাথে যুক্ত। ততক্ষণে, একটি সমবাহু হাইপারবোলার চতুর্ভুজ এবং প্রাকৃতিক লগারিদমের মধ্যে সংযোগ প্রতিষ্ঠিত হয়েছিল। এই সময়ের লগারিদমের তত্ত্বটি অনেক গণিতবিদদের নামের সাথে যুক্ত।

জার্মান গণিতবিদ, জ্যোতির্বিদ এবং প্রকৌশলী নিকোলাস মার্কেটর তার প্রবন্ধে

"লগারিথমোটেকনিক্স" (1668) একটি সিরিজ দেয় যা ln(x + 1) এর পরিপ্রেক্ষিতে বিস্তৃতি দেয়

ক্ষমতা x:

এই অভিব্যক্তিটি তার চিন্তাধারার সাথে হুবহু মিলে যায়, যদিও তিনি অবশ্যই d, ... চিহ্ন ব্যবহার করেননি, তবে আরও কষ্টকর চিহ্ন ব্যবহার করেননি। লগারিদমিক সিরিজ আবিষ্কারের সাথে সাথে লগারিদম গণনা করার কৌশল পরিবর্তিত হয়: তারা অসীম সিরিজ ব্যবহার করে নির্ধারণ করা শুরু করে। 1907-1908 সালে পড়া "উচ্চতর দৃষ্টিকোণ থেকে প্রাথমিক গণিত" বক্তৃতাগুলিতে, এফ. ক্লেইন লগারিদমের তত্ত্ব গঠনের জন্য সূত্রটিকে একটি সূচনা বিন্দু হিসাবে ব্যবহার করার পরামর্শ দিয়েছিলেন।

পর্যায় 3

বিপরীতের একটি ফাংশন হিসাবে লগারিদমিক ফাংশনের সংজ্ঞা

সূচকীয়, প্রদত্ত বেসের সূচক হিসাবে লগারিদম

তাৎক্ষণিকভাবে প্রণয়ন করা হয়নি। লিওনহার্ড অয়লারের কাজ (1707-1783)

"ইনফিনিটিসিমালের বিশ্লেষণের ভূমিকা" (1748) আরও কাজ করেছে

লগারিদমিক ফাংশনের তত্ত্বের বিকাশ। এইভাবে,

লগারিদম প্রথম চালু হওয়ার পর 134 বছর কেটে গেছে

(1614 থেকে গণনা) গণিতবিদরা একটি সংজ্ঞা নিয়ে আসার আগে

লগারিদমের ধারণা, যা এখন স্কুল কোর্সের ভিত্তি।

অধ্যায় 2. লগারিদমিক অসমতার সংগ্রহ

2.1। সমতুল্য রূপান্তর এবং ব্যবধানের সাধারণীকৃত পদ্ধতি।

সমতুল্য রূপান্তর

যদি a > 1

যদি 0 < а < 1

সাধারণ ব্যবধান পদ্ধতি

এই পদ্ধতিটি প্রায় যেকোনো ধরনের বৈষম্য সমাধানে সর্বজনীন। সমাধান স্কিম এই মত দেখায়:

1. অসমতাকে এমন একটি ফর্মে আনুন, যেখানে ফাংশনটি বাম দিকে অবস্থিত
, এবং ডানদিকে 0।

2. ফাংশনের সুযোগ সন্ধান করুন
.

3. একটি ফাংশনের শূন্য খুঁজুন
, অর্থাৎ সমীকরণটি সমাধান করুন
(এবং একটি সমীকরণ সমাধান করা সাধারণত অসমতা সমাধানের চেয়ে সহজ)।

4. একটি বাস্তব রেখায় ফাংশনের সংজ্ঞা এবং শূন্যের ডোমেন আঁকুন।

5. ফাংশনের লক্ষণ নির্ণয় কর
প্রাপ্ত বিরতিতে।

6. ফাংশনটি প্রয়োজনীয় মান গ্রহণ করে এমন বিরতিগুলি নির্বাচন করুন এবং উত্তরটি লিখুন।

উদাহরণ 1

সমাধান:

ব্যবধান পদ্ধতি প্রয়োগ করুন

কোথায়

এই মানের জন্য, লগারিদমের চিহ্নের অধীনে সমস্ত রাশি ইতিবাচক।

উত্তর:

উদাহরণ 2

সমাধান:

১ম উপায় . ODZ অসমতা দ্বারা নির্ধারিত হয় এক্স> 3. এই ধরনের জন্য লগারিদম নেওয়া এক্সবেস 10 এ, আমরা পাই

শেষ অসমতা পচন নিয়ম প্রয়োগ করে সমাধান করা যেতে পারে, যেমন শূন্যের সাথে ফ্যাক্টর তুলনা করা। যাইহোক, এই ক্ষেত্রে ফাংশনের স্থিরতার ব্যবধান নির্ধারণ করা সহজ

তাই ব্যবধান পদ্ধতি প্রয়োগ করা যেতে পারে।

ফাংশন চ(এক্স) = 2এক্স(এক্স- 3.5)lgǀ এক্স- 3ǀ এর জন্য একটানা এক্স> 3 এবং পয়েন্টে অদৃশ্য হয়ে যায় এক্স 1 = 0, এক্স 2 = 3,5, এক্স 3 = 2, এক্স 4 = 4. এইভাবে, আমরা ফাংশনের স্থিরতার ব্যবধান নির্ধারণ করি চ(এক্স):

উত্তর:

২য় উপায় . চলুন সরাসরি মূল অসমতার ক্ষেত্রে ব্যবধানের পদ্ধতির ধারণাগুলি প্রয়োগ করা যাক।

এই জন্য, আমরা যে অভিব্যক্তি প্রত্যাহার কখ- কগ এবং ( ক - 1)(খ- 1) একটি চিহ্ন আছে. তাহলে আমাদের বৈষম্য এক্স> 3 অসমতার সমতুল্য

বা

শেষ অসমতা ব্যবধান পদ্ধতি দ্বারা সমাধান করা হয়

উত্তর:

উদাহরণ 3

সমাধান:

ব্যবধান পদ্ধতি প্রয়োগ করুন

উত্তর:

উদাহরণ 4

সমাধান:

2 সাল থেকে এক্স 2 - 3এক্সসব বাস্তবের জন্য + 3 > 0 এক্স, তারপর

দ্বিতীয় অসমতা সমাধান করতে, আমরা ব্যবধান পদ্ধতি ব্যবহার করি

প্রথম অসমতায়, আমরা পরিবর্তন করি

তাহলে আমরা 2y 2-এ অসমতায় পৌঁছাব y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, যা অসমতা পূরণ করে -0.5< y < 1.

কোথা থেকে, কারণ

আমরা অসমতা পেতে

যা দিয়ে বাহিত হয় এক্স, যার জন্য 2 এক্স 2 - 3এক্স - 5 < 0. Вновь применим метод интервалов

এখন, সিস্টেমের দ্বিতীয় অসমতার সমাধান বিবেচনা করে, আমরা অবশেষে প্রাপ্ত করি

উত্তর:

উদাহরণ 5

সমাধান:

অসমতা সিস্টেমের একটি সেটের সমতুল্য

বা

ব্যবধান পদ্ধতি বা প্রয়োগ করুন

উত্তর:

উদাহরণ 6

সমাধান:

বৈষম্য একটি সিস্টেমের সমতুল্য

দিন

তারপর y > 0,

এবং প্রথম অসমতা

সিস্টেম রূপ নেয়

অথবা, প্রসারিত হচ্ছে

গুণনীয়ক বর্গাকার ত্রিনামিক,

শেষ অসমতার জন্য ব্যবধান পদ্ধতি প্রয়োগ করা,

আমরা দেখতে যে এর সমাধান শর্ত সন্তুষ্ট y> 0 সব হবে y > 4.

এইভাবে, মূল অসমতা সিস্টেমের সমতুল্য:

তাই, বৈষম্যের সমাধান সবই

2.2। যৌক্তিককরণ পদ্ধতি।

পূর্বে, বৈষম্যের যৌক্তিককরণের পদ্ধতিটি সমাধান করা হয়নি, এটি জানা ছিল না। এটি "সূচক এবং লগারিদমিক অসমতা সমাধানের জন্য একটি নতুন আধুনিক কার্যকর পদ্ধতি" (কোলেসনিকোভা S.I. এর বই থেকে উদ্ধৃতি)
এবং এমনকি যদি শিক্ষক তাকে চিনতেন, একটি ভয় ছিল - তবে ইউএসই বিশেষজ্ঞ কি তাকে চেনেন এবং কেন তারা তাকে স্কুলে দেয় না? এমন পরিস্থিতি ছিল যখন শিক্ষক ছাত্রকে বলেছিলেন: "আপনি এটি কোথায় পেয়েছেন? বসুন - 2।"
এখন পদ্ধতিটি সর্বত্র প্রচার করা হচ্ছে। এবং বিশেষজ্ঞদের জন্য, এই পদ্ধতির সাথে সম্পর্কিত নির্দেশিকা রয়েছে এবং সমাধান C3-তে "মানক বিকল্পগুলির সর্বাধিক সম্পূর্ণ সংস্করণ ..." এ, এই পদ্ধতিটি ব্যবহার করা হয়েছে।
পদ্ধতিটি দুর্দান্ত!

"ম্যাজিক টেবিল"

অন্যান্য সূত্রে

যদি a>1 এবং b>1, তারপর a b>0 এবং (a -1)(b -1)>0 লগ করুন;

যদি a>1 এবং 0

যদি 0<ক<1 и b >1, তারপর লগ a b<0 и (a -1)(b -1)<0;

যদি 0<ক<1 и 00 এবং (a -1)(b -1)>0.

উপরের যুক্তিটি সহজ, কিন্তু লক্ষণীয়ভাবে লগারিদমিক অসমতার সমাধানকে সরল করে।

উদাহরণ 4

লগ x (x 2 -3)<0

সমাধান:

উদাহরণ 5

লগ 2 x (2x 2 -4x +6)≤লগ 2 x (x 2 +x )

সমাধান:

উত্তর. (0; 0.5) U.

উদাহরণ 6

এই অসমতা সমাধানের জন্য, আমরা হর-এর পরিবর্তে (x-1-1) (x-1) এবং লবের পরিবর্তে গুণফল (x-1) (x-3-9 + x) লিখি।

উত্তর : (3;6)

উদাহরণ 7

উদাহরণ 8

2.3। অ-মানক প্রতিস্থাপন।

উদাহরণ 1

উদাহরণ 2

উদাহরণ 3

উদাহরণ 4

উদাহরণ 5

উদাহরণ 6

উদাহরণ 7

লগ 4 (3 x -1) লগ 0.25

y=3 x -1 প্রতিস্থাপন করা যাক; তাহলে এই অসমতা রূপ নেয়

লগ 4 লগ 0.25
.

কারণ লগ 0.25 = -লগ 4 = -(log 4 y -log 4 16)=2-log 4 y , তারপর আমরা শেষ অসমতাটিকে 2log 4 y -log 4 2 y ≤ হিসাবে পুনরায় লিখি।

একটি প্রতিস্থাপন করা যাক t =log 4 y এবং অসমতা পাই t 2 -2t +≥0, যার সমাধান হল বিরতিগুলি - .

এইভাবে, y-এর মান খুঁজে পেতে, আমাদের কাছে দুটি সহজ অসমতার একটি সেট আছে
এই সংগ্রহের সমাধান হল ব্যবধান 0<у≤2 и 8≤у<+.

অতএব, মূল অসমতা দুটি সূচকীয় অসমতার সমতুল্য,
অর্থাৎ, সমষ্টি

এই সেটের প্রথম অসমতার সমাধান হল ব্যবধান 0<х≤1, решением второго – промежуток 2≤х<+. এইভাবে, মূল অসমতা 0 থেকে x এর সমস্ত মানের জন্য ধারণ করে<х≤1 и 2≤х<+.

উদাহরণ 8

সমাধান:

বৈষম্য একটি সিস্টেমের সমতুল্য

দ্বিতীয় অসমতার সমাধান, যা ODZ নির্ধারণ করে, সেগুলির সেট হবে এক্স,

কিসের জন্য এক্স > 0.

প্রথম অসমতা সমাধান করতে, আমরা পরিবর্তন করতে

তারপর আমরা অসমতা পেতে

বা

পদ্ধতি দ্বারা শেষ অসমতার সমাধানের সেট পাওয়া যায়

বিরতি: -1< t < 2. Откуда, возвращаясь к переменной এক্স, আমরা পেতে

বা

যারা অনেক এক্স, যা শেষ অসমতা সন্তুষ্ট

ODZ এর অন্তর্গত ( এক্স> 0), অতএব, সিস্টেমের একটি সমাধান,

এবং তাই মূল অসমতা।

উত্তর:

2.4। ফাঁদ সঙ্গে কাজ.

উদাহরণ 1

.

সমাধান।অসমতার ODZ হল সমস্ত x শর্ত 0 সন্তুষ্ট . অতএব, ব্যবধান 0 থেকে সমস্ত x

উদাহরণ 2

লগ 2 (2x +1-x 2)>লগ 2 (2x-1 +1-x)+1।. ? বিন্দু হল যে দ্বিতীয় সংখ্যাটি স্পষ্টতই এর চেয়ে বেশি

উপসংহার

বিভিন্ন শিক্ষামূলক উত্সের একটি বৃহৎ বৈচিত্র্য থেকে C3 সমস্যা সমাধানের জন্য বিশেষ পদ্ধতিগুলি খুঁজে পাওয়া সহজ ছিল না। কাজ চলাকালীন, আমি জটিল লগারিদমিক অসমতা সমাধানের জন্য অ-মানক পদ্ধতিগুলি অধ্যয়ন করতে সক্ষম হয়েছি। এগুলি হল: সমতুল্য রূপান্তর এবং ব্যবধানের সাধারণীকৃত পদ্ধতি, যৌক্তিককরণের পদ্ধতি , অ-মানক প্রতিস্থাপন , ODZ ফাঁদ সঙ্গে কাজ. স্কুলের পাঠ্যক্রমে এই পদ্ধতিগুলি অনুপস্থিত।

বিভিন্ন পদ্ধতি ব্যবহার করে, আমি C3 নামক অংশে USE-এ দেওয়া 27টি অসমতার সমাধান করেছি। পদ্ধতি দ্বারা সমাধানের সাথে এই অসমতাগুলি "সমাধানের সাথে লগারিদমিক C3 অসমতা" সংগ্রহের ভিত্তি তৈরি করেছে, যা আমার কার্যকলাপের প্রকল্প পণ্য হয়ে উঠেছে। প্রকল্পের শুরুতে আমি যে হাইপোথিসিসটি সামনে রেখেছিলাম তা নিশ্চিত করা হয়েছিল: এই পদ্ধতিগুলি জানা থাকলে C3 সমস্যাগুলি কার্যকরভাবে সমাধান করা যেতে পারে।

উপরন্তু, আমি লগারিদম সম্পর্কে আকর্ষণীয় তথ্য আবিষ্কার করেছি। এটা আমার জন্য আকর্ষণীয় ছিল. আমার প্রকল্প পণ্য ছাত্র এবং শিক্ষক উভয় জন্য দরকারী হবে.

উপসংহার:

এইভাবে, প্রকল্পের লক্ষ্য অর্জিত হয়, সমস্যা সমাধান করা হয়। এবং আমি কাজের সব পর্যায়ে প্রকল্প কার্যক্রমের সবচেয়ে সম্পূর্ণ এবং বহুমুখী অভিজ্ঞতা পেয়েছি। প্রকল্পে কাজ করার সময়, আমার প্রধান উন্নয়নমূলক প্রভাব ছিল মানসিক দক্ষতা, যৌক্তিক মানসিক ক্রিয়াকলাপ সম্পর্কিত কার্যকলাপ, সৃজনশীল দক্ষতার বিকাশ, ব্যক্তিগত উদ্যোগ, দায়িত্ব, অধ্যবসায় এবং কার্যকলাপের উপর।

একটি গবেষণা প্রকল্প তৈরি করার সময় সাফল্যের একটি গ্যারান্টি আমি হয়েছি: গুরুত্বপূর্ণ স্কুল অভিজ্ঞতা, বিভিন্ন উত্স থেকে তথ্য আহরণ করার ক্ষমতা, এর নির্ভরযোগ্যতা পরীক্ষা করুন, তাত্পর্য অনুসারে এটিকে স্থান দিন।

গণিতে সরাসরি বিষয় জ্ঞান ছাড়াও, তিনি কম্পিউটার বিজ্ঞানের ক্ষেত্রে তার ব্যবহারিক দক্ষতা প্রসারিত করেছেন, মনোবিজ্ঞানের ক্ষেত্রে নতুন জ্ঞান এবং অভিজ্ঞতা অর্জন করেছেন, সহপাঠীদের সাথে যোগাযোগ স্থাপন করেছেন এবং প্রাপ্তবয়স্কদের সাথে সহযোগিতা করতে শিখেছেন। প্রকল্পের কার্যক্রম চলাকালীন, সাংগঠনিক, বুদ্ধিবৃত্তিক এবং যোগাযোগমূলক সাধারণ শিক্ষাগত দক্ষতা এবং ক্ষমতা বিকাশ করা হয়েছিল।

সাহিত্য

1. কোরিয়ানভ এ. জি., প্রোকোফিভ এ. এ. একটি পরিবর্তনশীল (সাধারণ কাজ C3) সহ অসমতার সিস্টেম।

2. মালকোভা এ.জি. গণিতে ইউনিফাইড স্টেট পরীক্ষার জন্য প্রস্তুতি নিচ্ছেন।

3. এস.এস. সামারোভা, লগারিদমিক অসমতার সমাধান।

4. গণিত। A.L. দ্বারা সম্পাদিত প্রশিক্ষণ কাজের সংগ্রহ। সেমিওনভ এবং আই.ভি. ইয়াশচেঙ্কো। -এম.: MTsNMO, 2009. - 72 p.-

তাদের সঙ্গে লগারিদম ভিতরে আছে.

উদাহরণ:

\(\log_3⁡x≥\log_3⁡9\)
\(\log_3⁡ ((x^2-3))< \log_3⁡{(2x)}\)
\(\log_(x+1)⁡((x^2+3x-7))>2\)
\(\lg^2⁡((x+1))+10≤11 \lg⁡((x+1))\)

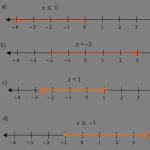
লগারিদমিক অসমতা কিভাবে সমাধান করবেন:

যেকোনো লগারিদমিক অসমতাকে \(\log_a⁡(f(x)) ˅ \log_a(⁡g(x))\) (প্রতীক \(˅\) মানে যেকোনও ) আকারে হ্রাস করা উচিত। এই ফর্মটি লগারিদমের অধীনে অভিব্যক্তির অসমতা, অর্থাৎ ফর্ম \(f(x) ˅ g(x)\) পাস করে লগারিদম এবং তাদের ভিত্তিগুলি থেকে পরিত্রাণ পেতে দেয়।

কিন্তু এই রূপান্তর করার সময়, একটি খুব গুরুত্বপূর্ণ সূক্ষ্মতা আছে:
\(-\) যদি - একটি সংখ্যা এবং এটি 1 এর থেকে বড় - অসমতার চিহ্নটি পরিবর্তনের সময় একই থাকে,
\(-\) যদি ভিত্তিটি 0-এর চেয়ে বড় কিন্তু 1-এর কম (শূন্য এবং একের মধ্যে) একটি সংখ্যা হয়, তাহলে অসমতার চিহ্নটি অবশ্যই বিপরীত হতে হবে, যেমন

উদাহরণ:

\(\log_2⁡((8-x))<1\) ODZ: \(8-x>0\) \(-x>-8\) \(এক্স<8\) সমাধান: \(\ লগ\)\(_2\) \((8-x)<\log\)\(_2\) \({2}\) \(8-x\)\(<\) \(2\) \(8-2\(x>6\) উত্তর: \((6;8)\)

\(\ লগ\)\(_(0.5⁡)\) \((2x-4)\)≥\(\log\)\(_(0.5)\) ⁡\((x+ এক))\) ODZ: \(\begin(cases)2x-4>0\\x+1 > 0\end(কেস)\) \(\begin(cases)2x>4\\x > -1\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)x>2\\x > -1\end(কেস) \) \(\Leftrightarrow\) \(x\in(2;\infty)\) সমাধান: \(2x-4\)\(≤\)\(x+1\) \(2x-x≤4+1\) \(x≤5\) উত্তর: \((2;5]\)

অনেক গুরুত্বপূর্ণ!যেকোনো অসমতায়, ফর্ম \(\log_a(⁡f(x)) ˅ \log_a⁡(g(x))\) থেকে লগারিদমের অধীনে অভিব্যক্তির তুলনা করার জন্য রূপান্তর শুধুমাত্র তখনই করা যেতে পারে যদি:

উদাহরণ . অসমতা সমাধান করুন: \(\log\)\(≤-1\)

সমাধান:

\(\ লগ\) \(_(\frac(1)(3))⁡(\frac(3x-2)(2x-3))\)\(≤-1\)	আসুন ODZ লিখি।
ODZ: \(\frac(3x-2)(2x-3)\) \(>0\)
\(⁡\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\)	আমরা বন্ধনী খুলি, দিতে.
\(⁡\frac(-3x+7)(2x-3)\) \(≥\) \(0\)	আমরা অসমতাকে \(-1\) দ্বারা গুণ করি, তুলনা চিহ্নটিকে বিপরীত করার কথা মনে রেখে।
\(⁡\frac(3x-7)(2x-3)\) \(≤\) \(0\)
\(⁡\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\)	আসুন একটি সংখ্যারেখা তৈরি করি এবং এর উপর \(\frac(7)(3)\) এবং \(\frac(3)(2)\) বিন্দুগুলি চিহ্নিত করি। উল্লেখ্য যে হর থেকে বিন্দুটি ছিদ্র করা হয়েছে, যদিও অসমতা কঠোর নয়। আসল বিষয়টি হ'ল এই বিন্দুটি কোনও সমাধান হবে না, যেহেতু অসমতার প্রতিস্থাপন করার সময়, এটি আমাদেরকে শূন্য দ্বারা বিভাজনের দিকে নিয়ে যাবে।
\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)	এখন আমরা একই সাংখ্যিক অক্ষে ODZ প্লট করি এবং উত্তরে ODZ-এর মধ্যে পড়ে থাকা ব্যবধানটি লিখি।
	চূড়ান্ত উত্তর লিখুন।

উত্তর: \(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

উদাহরণ . অসমতা সমাধান করুন: \(\log^2_3⁡x-\log_3⁡x-2>0\)

সমাধান:

\(\log^2_3⁡x-\log_3⁡x-2>0\)	আসুন ODZ লিখি।
ODZ: \(x>0\)	সিদ্ধান্তে আসা যাক।
সমাধান: \(\log^2_3⁡x-\log_3⁡x-2>0\)	আমাদের সামনে একটি সাধারণ বর্গ লগারিদমিক অসমতা। আমরা করি.
\(t=\log_3⁡x\) \(t^2-t-2>0\)	বৈষম্যের বাম দিকে প্রসারিত করুন।
\(D=1+8=9\) \(t_1= frac(1+3)(2)=2\) \(t_2=\frac(1-3)(2)=-1\) \(t+1)(t-2)>0\)
	এখন আপনাকে আসল ভেরিয়েবলে ফিরে যেতে হবে - x। এটি করার জন্য, আমরা পাস করি, যার একই সমাধান রয়েছে এবং বিপরীত প্রতিস্থাপন তৈরি করুন।
\(\left[ \begin(সংগৃহীত) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3⁡x>2 \\ \log_3⁡x<-1 \end{gathered} \right.\)	রূপান্তর \(2=\log_3⁡9\), \(-1=\log_3⁡\frac(1)(3)\।
\(\left[ \begin(সংগৃহীত) \log_3⁡x>\log_39 \\ \log_3⁡x<\log_3\frac{1}{3} \end{gathered} \right.\)	আসুন আর্গুমেন্ট তুলনা এগিয়ে যান. লগারিদমের ভিত্তিগুলি \(1\) এর চেয়ে বড়, তাই অসমতার চিহ্ন পরিবর্তন হয় না।
\(\left[ \begin(একত্রিত) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\)	আসুন একটি চিত্রে অসমতা এবং ODZ এর সমাধান একত্রিত করি।
	চলুন উত্তর লিখি।

উত্তর: \(0; \frac(1)(3))∪(9;∞)\)

সহজ লগারিদম অসমতা এবং অসমতার সমাধান, যেখানে লগারিদমের ভিত্তি স্থির করা হয়েছে, আমরা শেষ পাঠে বিবেচনা করেছি।

কিন্তু লগারিদমের ভিত্তি যদি একটি পরিবর্তনশীল হয়?

তাহলে আমরা উদ্ধারে আসব অসমতার যৌক্তিকতা।এটি কীভাবে কাজ করে তা বোঝার জন্য, আসুন বিবেচনা করা যাক, উদাহরণস্বরূপ, অসমতা:

$$\log_(2x) x^2 > \log_(2x) x.$$

প্রত্যাশিত হিসাবে, ODZ দিয়ে শুরু করা যাক।

ODZ

$$\left[ \begin(array)(l)x>0,\\ 2x ≠ 1. \end(array)\right.$$

বৈষম্যের সমাধান

আসুন আমরা একটি স্থির ভিত্তির সাথে একটি অসমতার সমাধান করছি। যদি ভিত্তিটি একের বেশি হয়, আমরা লগারিদমগুলি থেকে পরিত্রাণ পাই, এবং অসমতার চিহ্নটি পরিবর্তিত হয় না, যদি এটি একের চেয়ে কম হয় তবে এটি পরিবর্তিত হয়।

আসুন এটি একটি সিস্টেম হিসাবে লিখি:

$$\left[ \begin(array)(l) \left\( \begin(array)(l)2x>1,\\ x^2 > x; \end(array)\right। \\ \left\ ( \begin(array)(l)2x<1,\\ x^2 < x; \end{array}\right. \end{array} \right.$$

আরও যুক্তির জন্য, আমরা অসাম্যের সমস্ত ডানদিকে বাম দিকে স্থানান্তর করি।

$$\left[ \begin(array)(l) \left\( \begin(array)(l)2x-1>0,\\ x^2 -x>0; \end(array)\right। \ \ \ বাম \( \ শুরু(অ্যারে)(l)2x-1<0,\\ x^2 -x<0; \end{array}\right. \end{array} \right.$$

আমরা কি পেলাম? দেখা গেল যে আমাদের একই সময়ে ধনাত্মক বা ঋণাত্মক হওয়ার জন্য `2x-1` এবং `x^2 - x` অভিব্যক্তির প্রয়োজন। আমরা যদি অসমতা সমাধান করি তবে একই ফলাফল পাওয়া যাবে:

$$(2x-1)(x^2 - x) >0.$$

এই অসমতা, মূল সিস্টেমের মতো, যদি উভয় কারণই ইতিবাচক বা নেতিবাচক হয়। দেখা যাচ্ছে যে লগারিদমিক অসমতা থেকে যৌক্তিক একের দিকে যাওয়া সম্ভব (ODZ বিবেচনা করে)।

আসুন প্রণয়ন করি লগারিদমিক অসমতার জন্য যৌক্তিককরণ পদ্ধতি$$\log_(f(x)) g(x) \vee \log_(f(x)) h(x) \Leftrightarrow (f(x) - 1)(g(x)-h(x)) \ vee 0,$$ যেখানে `\vee` কোনো অসমতার চিহ্ন। (`>` চিহ্নের জন্য, আমরা কেবল সূত্রটির বৈধতা পরীক্ষা করেছি। বাকিদের জন্য, আমি এটি নিজে পরীক্ষা করার পরামর্শ দিচ্ছি - এইভাবে আপনি এটি আরও ভালভাবে মনে রাখবেন)।

আসুন আমাদের বৈষম্যের সমাধানে ফিরে আসি। বন্ধনীতে প্রসারিত করা (ফাংশনের শূন্যগুলি আরও ভালভাবে দেখতে), আমরা পাই

$$(2x-1)x(x - 1) >0.$$

ব্যবধান পদ্ধতি নিম্নলিখিত ছবি দেবে:

(যেহেতু অসমতা কঠোর এবং ব্যবধানের শেষগুলি আমাদের জন্য কোন আগ্রহের নয়, সেগুলি পূরণ করা হয় না।) দেখা যায়, প্রাপ্ত ব্যবধানগুলি ODZ-কে সন্তুষ্ট করে। উত্তর পেয়েছি: `(0,\frac(1)(2)) \cup (1,∞)`।

দ্বিতীয় উদাহরণ। পরিবর্তনশীল ভিত্তি সহ লগারিদমিক অসমতার সমাধান

$$\log_(2-x) 3 \leqslant \log_(2-x) x.$$

ODZ

$$\left\(\begin(array)(l)2-x > 0,\\ 2-x ≠ 1, \\ x > 0. \end(array)\right.$$

$$\left\(\begin(array)(l)x< 2,\\ x ≠ 1, \\ x >0. \end(অ্যারে)\right.$$

বৈষম্যের সমাধান

নিয়ম অনুযায়ী আমরা সবেমাত্র পেয়েছি লগারিদমিক অসমতার যৌক্তিকতা,আমরা পাই যে এই বৈষম্যটি নিম্নলিখিতগুলির সাথে অভিন্ন (ODZ বিবেচনা করে)

$$(2-x -1) (3-x) \leqslant 0.$$

$$(1-x) (3-x) \leqslant 0.$$

এই সমাধানটি ODZ-এর সাথে একত্রিত করলে, আমরা উত্তর পাই: `(1,2)`।

তৃতীয় উদাহরণ। একটি ভগ্নাংশের লগারিদম

$$\log_x\frac(4x+5)(6-5x) \leqslant -1.$$

ODZ

$$\left\(\begin(array)(l) \dfrac(4x+5)(6-5x)>0, \\ x>0,\\ x≠ 1.\end(অ্যারে) \right.$ $

যেহেতু সিস্টেমটি তুলনামূলকভাবে জটিল, আসুন অবিলম্বে সংখ্যা রেখায় অসমতার সমাধান প্লট করি:

সুতরাং, ODZ: `(0,1)\cup \left(1,\frac(6)(5)\right)`।

বৈষম্যের সমাধান

বেস `x` সহ লগারিদম হিসেবে `-1`কে উপস্থাপন করি।

$$\log_x\frac(4x+5)(6-5x) \leqslant \log_x x^(-1)।$$

ব্যবহার করে লগারিদমিক অসমতার যৌক্তিকতাআমরা একটি যৌক্তিক অসমতা পাই:

$$(x-1)\left(\frac(4x+5)(6-5x) -\frac(1)(x)\right)\leqslant0,$$

$$(x-1)\left(\frac(4x^2+5x - 6+5x)(x(6-5x))\right)\leqslant0,$$

$$(x-1)\left(\frac(2x^2+5x - 3)(x(6-5x))\right)\leqslant0.$$