Как да проверя в матрица. Обратна матрица и нейните свойства. Намиране на обратната матрица чрез гаусово елиминиране на неизвестните

Матрична алгебра - обратна матрица

обратна матрица

обратна матрицаНарича се матрица, която, когато се умножи както отдясно, така и отляво по дадена матрица, дава матрицата за идентичност.
Означете матрицата, обратна на матрицата НОпрез , тогава според дефиницията получаваме:

където Ее идентичната матрица.
квадратна матрицаНаречен неспециални (неизродени), ако неговият детерминант не е равен на нула. Иначе се нарича специален (изродени) или единствено число.

Има една теорема: всяка неособена матрица има обратна матрица.

Операцията за намиране на обратната матрица се нарича обжалванематрици. Помислете за алгоритъма за инверсия на матрицата. Нека е дадена неособена матрица н-та поръчка:

където Δ = дет А ≠ 0.

Допълнение на алгебрични елементиматрици н-та поръчка НОдетерминантата на матрицата ( н–1)-ти ред, получен чрез изтриване и-ти ред и j-та колона на матрицата НО:

Нека създадем т.нар прикаченматрица:

където са алгебричните допълнения на съответните елементи на матрицата НО.
Забележете, че алгебричните допълнения на редовите елементи на матрицата НОсе поставят в съответните колони на матрицата Ã , тоест матрицата се транспонира едновременно.
Разделяне на всички матрични елементи Ã на Δ - стойността на детерминанта на матрицата НО, получаваме обратната матрица като резултат:

Отбелязваме редица специални свойства на обратната матрица:
1) за дадена матрица НОнеговата обратна матрица е единственият;
2) ако има обратна матрица, тогава десен заден ходи ляв обратенматрици съвпадат с него;
3) специална (дегенерирана) квадратна матрица няма обратна матрица.

Основните свойства на обратната матрица:
1) детерминантата на обратната матрица и детерминантата на оригиналната матрица са реципрочни;
2) обратната матрица на произведението на квадратните матрици е равна на произведението на обратните матрици на факторите, взети в обратен ред:

3) транспонираната обратна матрица е равна на обратната матрица от дадената транспонирана матрица:

ПРИМЕР Изчислете матрицата, обратна на дадената.

АЛГЕБРАИЧНИ СЪБИРАНИ И МИНОРИ

Нека имаме детерминанта от трети ред: .

Незначителенсъответстващи на този елемент aijдетерминанта от трети ред се нарича детерминантата от втори ред, получена от дадения чрез изтриване на реда и колоната, в пресечната точка на които стои дадения елемент, т.е. и-ти ред и j-та колона. Непълнолетни, съответстващи на даден елемент aijще обозначим M ij.

Например, незначителен M12съответстващ на елемента а 12, ще има детерминант 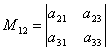, което се получава чрез изтриване на 1-ви ред и 2-ра колона от дадения детерминант.

Така формулата, която определя детерминантата от трети ред, показва, че тази детерминанта е равна на сбора от произведенията на елементите от 1-ви ред и съответните им минорни; докато минорът, съответстващ на елемента а 12, се взема със знака “–”, т.е. може да се напише така

.

(1)

По подобен начин може да се въведат дефиниции на минорите за детерминанти от втори и по-висок ред.

Нека представим още една концепция.

Алгебрично събиранеелемент aijдетерминанта се нарича неин минор M ijумножено по (–1) i+j .

Алгебрично събиране на елементи aijобозначено A ij.

От определението получаваме, че връзката между алгебричното допълнение на елемент и неговия минор се изразява с равенството A ij= (–1) i+j M ij .

Например,

Пример.Даден е детерминант. намирам A 13 , A 21 , A 32.

Лесно е да се види, че използвайки алгебрични събирания на елементи, формула (1) може да бъде написана като:

Подобно на тази формула, може да се получи разлагането на детерминанта върху елементите на всеки ред или колона.

Например разлагането на детерминанта върху елементите от 2-ри ред може да се получи по следния начин. Според свойство 2 на детерминанта имаме:

Нека разширим получената детерминанта с елементите от 1-ви ред.

.

(2)

Оттук защото детерминантите от втори ред във формула (2) са минорите на елементите а 21, а 22, а 23. Така, т.е. получихме разширението на детерминантата по елементите от 2-ри ред.

По подобен начин може да се получи разлагането на детерминанта върху елементите от третия ред. Използвайки свойство 1 на детерминанти (при транспониране), може да се покаже, че подобни разширения са валидни и за разширения в елементи на колона.

Следователно следната теорема е вярна.

Теорема (за разширяване на детерминантата в даден ред или колона).Детерминантата е равна на сбора от произведенията на елементите на всеки от неговите редове (или колони) и техните алгебрични допълнения.

Всичко по-горе е вярно за детерминанти от всеки по-висок порядък.

Примери.

ОБРАТНА МАТРИЦА

Концепцията за обратна матрица се въвежда само за квадратни матрици.

Ако Атогава е квадратна матрица обратенза него матрицата е означена матрица A-1и удовлетворяване на условието. (Това определение е въведено по аналогия с умножението на числата)

Тази тема е една от най-мразените сред студентите. По-лошо, вероятно, само детерминанти.

Номерът е, че самата концепция за обратния елемент (а сега не говоря само за матрици) ни препраща към операцията на умножение. Дори в училищната програма умножението се счита за сложна операция, а умножението на матрици като цяло е отделна тема, на която имам цял параграф и видео урок, посветен на него.

Днес няма да навлизаме в детайлите на матричните изчисления. Само запомнете: как се обозначават матриците, как се умножават и какво следва от това.

Преглед: Матрично умножение

Първо, нека се споразумеем за нотацията. Матрица $A$ с размер $\left[ m\times n \right]$ е просто таблица с числа с точно $m$ редове и $n$ колони:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrix) \right])_(n)\]

За да не объркате случайно редове и колони на места (повярвайте ми, на изпита можете да объркате единица с двойка - какво да кажем за някои редове там), просто погледнете снимката:

Определяне на индекси за матрични клетки

Какво се случва? Ако поставим стандартната координатна система $OXY$ в горния ляв ъгъл и насочим осите така, че да покриват цялата матрица, тогава всяка клетка от тази матрица може да бъде уникално свързана с координатите $\left(x;y \right) $ - това ще бъде номерът на ред и колона.

Защо координатната система е поставена точно в горния ляв ъгъл? Да, защото от там започваме да четем всякакви текстове. Много е лесно да се запомни.

Защо оста $x$ е насочена надолу, а не надясно? Отново е просто: вземете стандартната координатна система (оста $x$ върви надясно, оста $y$ върви нагоре) и я завъртете така, че да обхваща матрицата. Това е завъртане на 90 градуса по посока на часовниковата стрелка - виждаме неговия резултат на снимката.

Като цяло разбрахме как да определим индексите на матричните елементи. Сега нека се заемем с умножението.

Определение. Матриците $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когато броят на колоните в първата съвпада с броя на редовете във втората, са наречен последователен.

В този ред е. Човек може да бъде двусмислен и да каже, че матриците $A$ и $B$ образуват подредена двойка $\left(A;B \right)$: ако те са последователни в този ред, тогава изобщо не е необходимо $B $ и $A$, тези. двойката $\left(B;A \right)$ също е последователна.

Могат да се умножават само последователни матрици.

Определение. Произведението на последователни матрици $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ е новата матрица $C=\left[ m\times k \right ]$ , чиито елементи $((c)_(ij))$ се изчисляват по формулата:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

С други думи: за да получите елемента $((c)_(ij))$ от матрицата $C=A\cdot B$, трябва да вземете $i$-реда на първата матрица, $j$ -та колона на втората матрица и след това умножете елементи от този ред и колона. Съберете резултатите.

Да, това е грубо определение. От него веднага следват няколко факта:

1. Най-общо казано, матричното умножение е некомутативно: $A\cdot B\ne B\cdot A$;
2. Умножението обаче е асоциативно: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. И дори разпределителен: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. И отново разпределително: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Дистрибутивността на умножението трябваше да бъде описана отделно за лявата и дясната сума на множителя само поради некомутативността на операцията за умножение.

Ако все пак се окаже, че $A\cdot B=B\cdot A$, такива матрици се наричат ​​пермутируеми.

Сред всички матрици, които се умножават по нещо там, има специални - тези, които, когато се умножат по която и да е матрица $A$, отново дават $A$:

Определение. Матрица $E$ се нарича идентичност, ако $A\cdot E=A$ или $E\cdot A=A$. В случай на квадратна матрица $A$ можем да запишем:

Идентичността на матрицата е чест гост при решаването на матрични уравнения. И като цяло чест гост в света на матриците. :)

И заради този $E$ някой измисли цялата игра, която ще бъде написана по-нататък.

Какво е обратна матрица

Тъй като умножението на матрицата е много отнемаща време операция (трябва да умножите куп редове и колони), концепцията за обратна матрица също не е най-тривиалната. И има нужда от някакво обяснение.

Ключова дефиниция

Е, време е да разберем истината.

Определение. Матрицата $B$ се нарича обратна на матрицата $A$ if

Обратната матрица се обозначава с $((A)^(-1))$ (да не се бърка със степента!), така че дефиницията може да бъде пренаписана по следния начин:

Изглежда, че всичко е изключително просто и ясно. Но когато анализираме такова определение, веднага възникват няколко въпроса:

1. Винаги ли съществува обратна матрица? И ако не винаги, тогава как да определим: кога съществува и кога не?
2. И кой каза, че такава матрица е точно една? Ами ако за някаква оригинална матрица $A$ има цяла тълпа обратни?
3. Как изглеждат всички тези "обрати"? И как всъщност ги броиш?

Що се отнася до алгоритмите за изчисление - ще говорим за това малко по-късно. Но на останалите въпроси ще отговорим точно сега. Нека ги подредим под формата на отделни твърдения-леми.

Основни свойства

Нека започнем с това как трябва да изглежда матрицата $A$, за да има $((A)^(-1))$. Сега ще се уверим, че и двете матрици трябва да са квадратни и с еднакъв размер: $\left[ n\times n \right]$.

Лема 1. Дадена е матрица $A$ и нейната инверсия $((A)^(-1))$. Тогава и двете матрици са квадратни и имат същия ред $n$.

Доказателство. Всичко е просто. Нека матрицата $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Тъй като продуктът $A\cdot ((A)^(-1))=E$ съществува по дефиниция, матриците $A$ и $((A)^(-1))$ са последователни в този ред:

\[\begin(подравняване) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( подравняване)\]

Това е пряко следствие от алгоритъма за умножение на матрицата: коефициентите $n$ и $a$ са "транзитни" и трябва да са равни.

В същото време е дефинирано и обратното умножение: $((A)^(-1))\cdot A=E$, така че матриците $((A)^(-1))$ и $A$ са също последователно в този ред:

\[\begin(подравняване) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( подравняване)\]

По този начин, без да губим общността, можем да приемем, че $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Въпреки това, според дефиницията на $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, така че размерите на матриците са абсолютно еднакви:

\[\begin(подравняване) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Така се оказва, че и трите матрици - $A$, $((A)^(-1))$ и $E$ - са квадратни по размер $\left[ n\times n \right]$. Лемата е доказана.

Е, това вече е добре. Виждаме, че само квадратните матрици са обратими. Сега нека се уверим, че обратната матрица е винаги една и съща.

Лема 2. Дадена е матрица $A$ и нейната инверсия $((A)^(-1))$. Тогава тази обратна матрица е уникална.

Доказателство. Нека започнем от обратното: нека матрицата $A$ има поне две инверсни инстанции — $B$ и $C$. Тогава, според дефиницията, следните равенства са верни:

\[\begin(подравняване) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(подравняване)\]

От лема 1 заключаваме, че всичките четири матрици $A$, $B$, $C$ и $E$ са квадратни от същия ред: $\left[ n\times n \right]$. Следователно продуктът се определя:

Тъй като умножението на матрицата е асоциативно (но не и комутативно!), можем да запишем:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\rightarrow B=C. \\ \end(подравняване)\]

Получихме единствената възможна опция: две копия на обратната матрица са равни. Лемата е доказана.

Горните разсъждения почти дословно повтарят доказателството за уникалността на обратния елемент за всички реални числа $b\ne 0$. Единственото значително допълнение е вземането под внимание на размерността на матриците.

Все още обаче не знаем нищо за това дали някоя квадратна матрица е обратима. Тук на помощ ни идва детерминантата – това е ключова характеристика за всички квадратни матрици.

Лема 3 . Дадена е матрица $A$. Ако матрицата $((A)^(-1))$, обратна на нея, съществува, тогава детерминантата на оригиналната матрица е различна от нула:

\[\вляво| A \right|\ne 0\]

Доказателство. Вече знаем, че $A$ и $((A)^(-1))$ са квадратни матрици с размер $\left[ n\times n \right]$. Следователно за всеки от тях е възможно да се изчисли детерминантата: $\left| A \right|$ и $\left| ((A)^(-1)) \right|$. Въпреки това, детерминантът на продукта е равен на произведението на детерминантите:

\[\вляво| A\cdot B \right|=\left| A \right|\cdot \left| B \вдясно|\Стрелка надясно \наляво| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \вдясно|\]

Но според дефиницията на $A\cdot ((A)^(-1))=E$ и детерминантът на $E$ винаги е равен на 1, така че

\[\begin(подравняване) & A\cdot ((A)^(-1))=E; \\ & \вляво| A\cdot ((A)^(-1)) \right|=\left| E\вдясно|; \\ & \вляво| A \right|\cdot \left| ((A)^(-1)) \вдясно|=1. \\ \end(подравняване)\]

Произведението на две числа е равно на едно само ако всяко от тези числа е различно от нула:

\[\вляво| A \right|\ne 0;\quad \left| ((A)^(-1)) \вдясно|\ne 0.\]

Така се оказва, че $\left| A \right|\ne 0$. Лемата е доказана.

Всъщност това изискване е съвсем логично. Сега ще анализираме алгоритъма за намиране на обратната матрица - и ще стане напълно ясно защо по принцип не може да съществува обратна матрица с нулева детерминанта.

Но първо, нека формулираме "спомагателна" дефиниция:

Определение. Дегенерираната матрица е квадратна матрица с размер $\left[ n\times n \right]$, чиято детерминанта е нула.

По този начин можем да твърдим, че всяка обратима матрица е неизродена.

Как да намерим обратната матрица

Сега ще разгледаме универсален алгоритъм за намиране на обратни матрици. Като цяло има два общоприети алгоритма и днес ще разгледаме втория.

Този, който ще разгледаме сега, е много ефективен за матрици с размер $\left[ 2\times 2 \right]$ и - отчасти - с размер $\left[ 3\times 3 \right]$. Но като се започне от размера $\left[ 4\times 4 \right]$ е по-добре да не се използва. Защо - сега ще разберете всичко.

Алгебрични допълнения

Приготви се. Сега ще има болка. Не, не се притеснявайте: красива медицинска сестра с пола, чорапи с дантела не ви идва и няма да ви инжектира в дупето. Всичко е много по-прозаично: алгебричните допълнения и Нейно Величество „Матрицата на Съюза“ идват при вас.

Да започнем с основния. Нека има квадратна матрица с размер $A=\left[ n\times n \right]$, чиито елементи са наречени $((a)_(ij))$. След това за всеки такъв елемент може да се дефинира алгебрично допълнение:

Определение. Алгебрично допълнение $((A)_(ij))$ към елемента $((a)_(ij))$ в $i$-тия ред и $j$-та колона на матрицата $A=\left [ n \times n \right]$ е конструкция на формата

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Където $M_(ij)^(*)$ е детерминантата на матрицата, получена от оригиналния $A$ чрез изтриване на същия $i$-ти ред и $j$-та колона.

Отново. Алгебричното допълнение към матричния елемент с координати $\left(i;j \right)$ се обозначава като $((A)_(ij))$ и се изчислява по схемата:

1. Първо, изтриваме $i$-реда и $j$-та колона от оригиналната матрица. Получаваме нова квадратна матрица и обозначаваме нейния детерминант като $M_(ij)^(*)$.
2. След това умножаваме този детерминант по $((\left(-1 \right))^(i+j))$ - в началото този израз може да изглежда умопомрачителен, но всъщност просто откриваме знака пред $ M_(ij)^(*) $.
3. Броим - получаваме точно число. Тези. алгебричното събиране е просто число, а не някаква нова матрица и т.н.

Самата матрица $M_(ij)^(*)$ се нарича допълнителен минор към елемента $((a)_(ij))$. И в този смисъл горното определение за алгебрично допълнение е частен случай на по-сложно определение – това, което разгледахме в урока за детерминанта.

Важна забележка. Всъщност в математиката за "възрастни" алгебричните допълнения се дефинират, както следва:

1. Взимаме $k$ редове и $k$ колони в квадратна матрица. В пресечната им точка получаваме матрица с размер $\left[ k\times k \right]$ — нейната детерминанта се нарича минор от ред $k$ и се означава с $((M)_(k))$.
2. След това зачертаваме тези "избрани" $k$ редове и $k$ колони. Отново получаваме квадратна матрица - нейната детерминанта се нарича допълнителен минор и се означава с $M_(k)^(*)$.
3. Умножете $M_(k)^(*)$ по $((\left(-1 \right))^(t))$, където $t$ е (внимание сега!) сумата от числата на всички избрани редове и колони. Това ще бъде алгебричното допълнение.

Обърнете внимание на третата стъпка: всъщност има сума от $2k$ условия! Друго нещо е, че за $k=1$ получаваме само 2 члена - това ще са едни и същи $i+j$ - "координатите" на елемента $((a)_(ij))$, за който сме търси алгебрично допълнение.

Така че днес използваме леко опростена дефиниция. Но както ще видим по-късно, това ще бъде повече от достатъчно. Много по-важно е следното:

Определение. Обединяващата матрица $S$ към квадратната матрица $A=\left[ n\times n \right]$ е нова матрица с размер $\left[ n\times n \right]$, която се получава от $A$ като замените $((a)_(ij))$ с алгебрични допълнения $((A)_(ij))$:

\\Стрелка надясно S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \right]\]

Първата мисъл, която възниква в момента на осъзнаване на тази дефиниция е „това е колко трябва да преброите общо!” Спокойно: трябва да броиш, но не толкова. :)

Е, всичко това е много хубаво, но защо е необходимо? Но защо.

Основна теорема

Да се ​​върнем малко назад. Не забравяйте, че в лема 3 се казва, че една обратима матрица $A$ винаги е неособена (тоест нейната детерминанта е различна от нула: $\left| A \right|\ne 0$).

Така че, обратното също е вярно: ако матрицата $A$ не е изродена, тогава тя винаги е обратима. И дори има схема за търсене $((A)^(-1))$. Виж това:

Теорема за обратната матрица. Нека е дадена квадратна матрица $A=\left[ n\times n \right]$ и нейният детерминант е различен от нула: $\left| A \right|\ne 0$. Тогава обратната матрица $((A)^(-1))$ съществува и се изчислява по формулата:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

И сега - все същото, но с четлив почерк. За да намерите обратната матрица, трябва:

1. Изчислете детерминанта $\left| A \right|$ и се уверете, че е различен от нула.
2. Компилирайте обединителната матрица $S$, т.е. пребройте 100500 алгебрични допълнения $((A)_(ij))$ и ги поставете на място $((a)_(ij))$.
3. Транспонирайте тази матрица $S$ и след това я умножете по някакво число $q=(1)/(\left| A \right|)\;$.

И това е! Намерена е обратната матрица $((A)^(-1))$. Нека разгледаме примери:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

Решение. Нека проверим обратимостта. Нека изчислим детерминанта:

\[\вляво| A \вдясно|=\ляво| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Детерминантата е различна от нула. Така че матрицата е обратима. Нека създадем матрица на съюза:

Нека изчислим алгебричните допълнения:

\[\begin(подравняване) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\вдясно|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\вдясно|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \вдясно|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\вдясно|=3. \\ \end(подравняване)\]

Обърнете внимание: детерминанти |2|, |5|, |1| и |3| са детерминантите на матрици с размер $\left[ 1\times 1 \right]$, а не модули. Тези. ако в детерминантите имаше отрицателни числа, не е необходимо да премахвате "минус".

Като цяло нашата матрица на съюза изглежда така:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (масив)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(масив) \вдясно]\]

Добре, всичко свърши сега. Проблема решен.

Отговор. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Задача. Намерете обратната матрица:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Решение. Отново разглеждаме детерминанта:

\[\begin(подравняване) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Детерминантата е различна от нула - матрицата е обратима. Но сега ще бъде най-малкият: трябва да преброите до 9 (девет, по дяволите!) Алгебрични допълнения. И всеки от тях ще съдържа квалификатора $\left[ 2\times 2 \right]$. летя:

\[\begin(матрица) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\end(matrix) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\end(matrix) \right|=2; \\ \end(матрица)\]

Накратко, матрицата на съюза ще изглежда така:

Следователно обратната матрица ще бъде:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\ край(масив) \вдясно]\]

Е, това е всичко. Ето отговора.

Отговор. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Както можете да видите, в края на всеки пример направихме проверка. В тази връзка важна забележка:

Не бъдете мързеливи да проверите. Умножете оригиналната матрица по намерената обратна - трябва да получите $E$.

Много по-лесно и по-бързо е да извършите тази проверка, отколкото да търсите грешка при по-нататъшни изчисления, когато, например, решавате матрично уравнение.

Алтернативен начин

Както казах, теоремата за обратната матрица работи добре за размерите $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (в последния случай не е толкова "страхотно" вече). ”), но за големите матрици започва тъгата.

Но не се притеснявайте: има алтернативен алгоритъм, който може да се използва за спокойно намиране на обратната дори за матрицата $\left[ 10\times 10 \right]$. Но, както често се случва, за да разгледаме този алгоритъм, се нуждаем от малко теоретична подготовка.

Елементарни трансформации

Сред различните трансформации на матрицата има няколко специални - те се наричат ​​елементарни. Има точно три такива трансформации:

1. Умножение. Можете да вземете $i$-тия ред (колона) и да го умножите по произволно число $k\ne 0$;
2. Добавяне. Добавете към $i$-тия ред (колона) всеки друг $j$-ти ред (колона), умножен по произволно число $k\ne 0$ (разбира се, $k=0$ също е възможно, но какъв е смисълът от това? ?Нищо обаче няма да се промени).
3. Пермутация. Вземете $i$-тия и $j$-тия ред (колони) и ги разменете.

Защо тези трансформации се наричат ​​елементарни (за големите матрици те не изглеждат толкова елементарни) и защо са само три – тези въпроси са извън обхвата на днешния урок. Затова няма да навлизаме в подробности.

Друго нещо е важно: трябва да извършим всички тези извращения върху свързаната матрица. Да, да, правилно чухте. Сега ще има още едно определение – последното в днешния урок.

Приложена матрица

Със сигурност в училище сте решавали системи от уравнения, използвайки метода на събиране. Е, там, извадете друг от един ред, умножете един ред по число - това е всичко.

И така: сега всичко ще бъде същото, но вече „по възрастен начин“. Готов?

Определение. Нека са дадени матрицата $A=\left[ n\times n \right]$ и идентичната матрица $E$ със същия размер $n$. Тогава асоциираната матрица $\left[ A\left| д\вдясно. \right]$ е нова $\left[ n\times 2n \right]$ матрица, която изглежда така:

\[\left[ A\left| д\вдясно. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Накратко, вземаме матрицата $A$, вдясно й приписваме матрицата за идентичност $E$ с необходимия размер, разделяме ги с вертикална черта за красота - ето ви приложената. :)

Каква е уловката? И ето какво:

Теорема. Нека матрицата $A$ е обратима. Да разгледаме присъединената матрица $\left[ A\left| д\вдясно. \вдясно]$. Ако използвате елементарни трансформации на низовеприведете го до вида $\left[ E\left| Ярък. \вдясно]$, т.е. чрез умножаване, изваждане и пренареждане на редове, за да получите матрицата $E$ вдясно от $A$, тогава матрицата $B$, получена отляво, е обратната на $A$:

\[\left[ A\left| д\вдясно. \вдясно]\до \наляво[E\ляво| Ярък. \надясно]\Стрелка надясно B=((A)^(-1))\]

Толкова е просто! Накратко, алгоритъмът за намиране на обратната матрица изглежда така:

1. Напишете асоциираната матрица $\left[ A\left| д\вдясно. \вдясно]$;
2. Извършвайте елементарни преобразувания на низове, докато дясното вместо $A$ се появи $E$;
3. Разбира се, нещо ще се появи и отляво - определена матрица $B$. Това ще бъде обратното;
4. ПЕЧАЛБИ! :)

Разбира се, много по-лесно е да се каже, отколкото да се направи. Така че нека разгледаме няколко примера: за размерите $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.

Задача. Намерете обратната матрица:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Решение. Ние съставяме приложената матрица:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 и 1 \\\край(масив) \вдясно]\]

Тъй като последната колона на оригиналната матрица е пълна с единици, извадете първия ред от останалите:

\[\begin(подравняване) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(масив) \вдясно]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matrix)\to \\ & \to \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(масив) \вдясно] \\ \end(подравняване)\]

Няма повече единици, освен първия ред. Но ние не го докосваме, в противен случай новоотстранените единици ще започнат да се "умножават" в третата колона.

Но можем да извадим втория ред два пъти от последния - получаваме единица в долния ляв ъгъл:

\[\begin(подравняване) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(масив) \вдясно]\начало(матрица) \ \\ \надолу \\ -2 \\\end(матрица)\до \\ & \наляво [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \вдясно] \\ \end(подравняване)\]

Сега можем да извадим последния ред от първия и два пъти от втория - по този начин ще „нулираме“ първата колона:

\[\begin(подравняване) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(matrix) \right]\begin(matrix) -1 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \ към \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \вдясно] \\ \end(подравняване)\]

Умножете втория ред по −1 и след това го извадете 6 пъти от първия и добавете 1 път към последния:

\[\begin(подравняване) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\край(масив) \вдясно]\начало(матрица) \ \\ \ляво| \cdot \left(-1 \right) \right. \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -6 \\ \стрелка надолу \\ +1 \\\end (матрица)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(масив) \вдясно] \\ \end(подравняване)\]

Остава само да размените редове 1 и 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\край(масив) \вдясно]\]

Готов! Вдясно е необходимата обратна матрица.

Отговор. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Задача. Намерете обратната матрица:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\край (матрица) \вдясно]\]

Решение. Отново съставяме приложеното:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Да вземем малко назаем, да се погрижим колко трябва да броим сега... и да започнем да броим. Като начало, ние „зануляваме“ първата колона, като изваждаме ред 1 от редове 2 и 3:

\[\begin(подравняване) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(масив) \вдясно]\начало(матрица) \надолу \\ -1 \\ -1 \\ \ \\\end(матрица)\до \\ & \to \left[ \begin(масив)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Наблюдаваме твърде много "минуси" в редове 2-4. Умножете всичките три реда по −1 и след това изгорете третата колона, като извадите ред 3 от останалите:

\[\begin(подравняване) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(масив) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \вляво| \cdot \left(-1 \right) \right. \\ \вляво| \cdot \left(-1 \right) \right. \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (масив) \вдясно]\begin(matrix) -2 \\ -1 \\ \стрелка нагоре \\ -2 \\\end(matrix)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Сега е време да "изпържите" последната колона на оригиналната матрица: извадете ред 4 от останалата част:

\[\begin(подравняване) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(масив ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Окончателно хвърляне: "изгарете" втората колона, като извадите ред 2 от ред 1 и 3:

\[\begin(подравняване) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( масив) \вдясно]\начало(матрица) 6 \\ \стрелка нагоре \\ -5 \\ \\\end(матрица)\до \\ & \to \left[ \begin(масив)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

И отново, идентичната матрица отляво, така че обратната отдясно. :)

Отговор. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(матрица) \вдясно]$

Добре, всичко свърши сега. Проверете сами - бракувам. :)

Нека има квадратна матрица от n-ти ред

Матрицата A -1 се нарича обратна матрицапо отношение на матрицата A, ако A * A -1 = E, където E е идентичната матрица от n-ти ред.

Матрица за идентичност- такава квадратна матрица, в която всички елементи по главния диагонал, преминаващи от горния ляв ъгъл към долния десен ъгъл, са единици, а останалите са нули, например:

обратна матрицаможе да съществува само за квадратни матрицитези. за тези матрици, които имат еднакъв брой редове и колони.

Теорема за условието за съществуване на обратна матрица

За да има една матрица обратна матрица, е необходимо и достатъчно тя да е неизродена.

Матрицата A = (A1, A2,...A n) се нарича неизродениако векторите на колоните са линейно независими. Броят на линейно независими вектори на колона на матрица се нарича ранг на матрицата. Следователно можем да кажем, че за да съществува обратна матрица, е необходимо и достатъчно рангът на матрицата да е равен на нейната размерност, т.е. r = n.

Алгоритъм за намиране на обратната матрица

1. Запишете матрицата A в таблицата за решаване на системи от уравнения по метода на Гаус и вдясно (на мястото на десните части на уравненията) й припишете матрица E.
2. Използвайки трансформациите на Йордан, приведете матрица A към матрица, състояща се от единични колони; в този случай е необходимо едновременно да се трансформира матрицата E.
3. Ако е необходимо, пренаредете редовете (уравненията) на последната таблица, така че матрицата за идентичност E да се получи под матрицата A на оригиналната таблица.
4. Напишете обратната матрица A -1, която е в последната таблица под матрицата E на оригиналната таблица.

Пример 1

За матрица A намерете обратната матрица A -1

Решение: Записваме матрицата A и вдясно присвояваме идентичната матрица E. Използвайки трансформациите на Йордан, намаляваме матрицата A до матрицата на идентичността E. Изчисленията са показани в Таблица 31.1.

Нека проверим правилността на изчисленията, като умножим оригиналната матрица A и обратната матрица A -1.

В резултат на умножението на матрицата се получава матрицата за идентичност. Следователно изчисленията са правилни.

Отговор:

Решение на матрични уравнения

Матричните уравнения могат да изглеждат така:

AX = B, XA = B, AXB = C,

където A, B, C са дадени матрици, X е желаната матрица.

Матричните уравнения се решават чрез умножаване на уравнението по обратни матрици.

Например, за да намерите матрицата от уравнение, трябва да умножите това уравнение по отляво.

Следователно, за да намерите решение на уравнението, трябва да намерите обратната матрица и да я умножите по матрицата от дясната страна на уравнението.

Други уравнения се решават по подобен начин.

Пример 2

Решете уравнението AX = B, ако

Решение: Тъй като обратното на матрицата е равно (виж пример 1)

Матричният метод в икономическия анализ

Заедно с други те също намират приложение матрични методи. Тези методи се основават на линейна и векторно-матрична алгебра. Такива методи се използват за целите на анализа на сложни и многоизмерни икономически явления. Най-често тези методи се използват, когато е необходимо да се сравни функционирането на организациите и техните структурни подразделения.

В процеса на прилагане на матричните методи за анализ могат да се разграничат няколко етапа.

На първия етапсе извършва формирането на система от икономически показатели и въз основа на нея се съставя матрица от изходни данни, която представлява таблица, в която номерата на системата са показани в отделните й редове (i = 1,2,....,n), а по вертикалните графики - номера на индикаторите (j = 1,2,....,m).

На втория етапза всяка вертикална колона се разкрива най-голямата от наличните стойности на индикаторите, която се приема като единица.

След това всички суми, отразени в тази колона, се разделят на най-голямата стойност и се формира матрица от стандартизирани коефициенти.

На третия етапвсички компоненти на матрицата са на квадрат. Ако те имат различно значение, тогава на всеки индикатор от матрицата се присвоява определен коефициент на тежест к. Стойността на последния се определя от експерт.

На последния четвърти етапнамерени стойности на оценките Rjгрупирани в ред на нарастване или намаляване.

Посочените по-горе матрични методи трябва да се използват например при сравнителен анализ на различни инвестиционни проекти, както и при оценка на други показатели за икономическа ефективност на организациите.

обратна матрицае матрица А -1, когато се умножи по което дадената начална матрица Адава матрицата за идентичност Е:

AA −1 = A −1 A =Е.

Метод на обратна матрица.

Метод на обратна матрица- това е един от най-разпространените методи за решаване на матрици и се използва за решаване на системи от линейни алгебрични уравнения (SLAE) в случаите, когато броят на неизвестните съответства на броя на уравненията.

Нека има система нлинейни уравнения с ннеизвестен:

Такава система може да се запише като матрично уравнение A*X=B,

където
- системна матрица,

- колона с неизвестни,

- колона със свободни коефициенти.

От полученото матрично уравнение изразяваме X, като умножаваме двете страни на матричното уравнение отляво по A-1, в резултат на което:

A -1 * A * X = A -1 * B

Знаейки това A-1*A=E, тогава E*X=A-1*Bили X=A-1*B.

Следващата стъпка е да се определи обратната матрица A-1и умножено по колоната със свободни членове Б.

Обратна матрица към матрица Асъществува само когато дет А≠ 0 . С оглед на това, при решаване на SLAE по метода на обратната матрица, първата стъпка е намирането дет А. Ако дет А≠ 0 , то системата има само едно решение, което може да се получи по метода на обратната матрица, ако det A = 0, тогава такава система метод на обратна матрицане е решен.

Обратно матрично решение.

Последователност от действия за обратни матрични решения:

1. Вземете детерминанта на матрицата А. Ако детерминантата е по-голяма от нула, ние решаваме обратната матрица допълнително, ако е равна на нула, тогава обратната матрица не може да бъде намерена тук.
2. Намиране на транспонираната матрица AT.
3. Търсим алгебрични допълнения, след което заменяме всички елементи на матрицата с техните алгебрични допълнения.
4. Събираме обратната матрица от алгебрични събирания: разделяме всички елементи на получената матрица на детерминанта на първоначално зададената матрица. Крайната матрица ще бъде желаната обратна матрица спрямо оригиналната.

Алгоритъмът по-долу обратни матрични решенияпо същество същото като по-горе, разликата е само в няколко стъпки: първо определяме алгебричните допълнения и след това изчисляваме матрицата на съюза ° С.

1. Разберете дали дадената матрица е квадратна. В случай на отрицателен отговор става ясно, че за него не може да има обратна матрица.
2. Разберете дали дадената матрица е квадратна. В случай на отрицателен отговор става ясно, че за него не може да има обратна матрица.
3. Изчисляваме алгебрични събирания.
4. Ние съставяме съюзната (взаимна, прикрепена) матрица ° С.
5. Ние съставяме обратна матрица от алгебрични допълнения: всички елементи на присъединената матрица ° Сразделено на детерминанта на началната матрица. Получената матрица ще бъде желаната обратна матрица спрямо дадената.
6. Проверяваме извършената работа: умножаваме началната и резултантната матрица, резултатът трябва да бъде матрицата за идентичност.

Това се прави най-добре с прикачена матрица.

Теорема: Ако присвоим идентична матрица от същия ред на квадратна матрица от дясната страна и трансформираме първоначалната матрица отляво в единична матрица, използвайки елементарни трансформации върху редове, тогава получената от дясната страна ще бъде обратна на първоначалната.

Пример за намиране на обратната матрица.

Упражнение. За матрица намерете обратното по метода на присъединената матрица.

Решение. Добавяме към дадената матрица НОвдясно, идентичната матрица от 2-ри ред:

Извадете 2-ра от 1-вия ред:

Извадете първите 2 от втория ред: