Формулата за промяна на основата на логаритъм. Естествен логаритъм, функция ln x. Две очевидни следствия от дефиницията на логаритъма

Приемлив диапазон (ODZ) на логаритъма

Сега нека поговорим за ограниченията (ODZ - областта на ​​допустимите стойности​​ на променливите).

Спомняме си, че например квадратният корен не може да се вземе от отрицателни числа; или ако имаме дроб, тогава знаменателят не може да бъде равен на нула. Има подобни ограничения за логаритмите:

Тоест и аргументът, и основата трябва да са по-големи от нула, а основата не може да бъде равна.

Защо така?

Нека започнем просто: да кажем това. Тогава, например, числото не съществува, тъй като независимо каква степен вдигаме, винаги се оказва. Освен това за никого не съществува. Но в същото време той може да бъде равен на всичко (по същата причина - равен е на всяка степен). Следователно обектът не представлява интерес и просто е изхвърлен от математиката.

Подобен проблем имаме и в случая: в каквато и да е положителна степен - това, но изобщо не може да се издигне на отрицателна степен, тъй като ще се получи разделение на нула (напомням ви това).

Когато сме изправени пред проблема за повишаване на дробна степен (който е представен като корен:. Например, (тоест), но не съществува.

Следователно негативните причини са по-лесни за изхвърляне, отколкото да се забъркваш с тях.

Е, тъй като основата а е само положителна за нас, то без значение в каква степен я повишим, винаги ще получим строго положително число. Така че аргументът трябва да е положителен. Например, то не съществува, тъй като няма да бъде отрицателно число в каквато и да е степен (и дори нула, следователно и то не съществува).

При задачи с логаритми първата стъпка е да запишете ODZ. ще дам пример:

Нека решим уравнението.

Припомнете си дефиницията: логаритъмът е степента, до която трябва да се повдигне основата, за да се получи аргумент. И според условието тази степен е равна на: .

Получаваме обичайното квадратно уравнение: . Решаваме го с помощта на теоремата на Виета: сумата от корените е равна, а произведението. Лесни за вземане, това са числа и.

Но ако веднага вземете и запишете и двете числа в отговора, можете да получите 0 точки за задачата. Защо? Нека помислим какво се случва, ако поставим тези корени в първоначалното уравнение?

Това е очевидно невярно, тъй като основата не може да бъде отрицателна, тоест коренът е „от трета страна“.

За да избегнете подобни неприятни трикове, трябва да запишете ODZ дори преди да започнете да решавате уравнението:

След това, след като получихме корените и, веднага изхвърляме корена и пишем правилния отговор.

Пример 1(опитайте се да го решите сами) :

Намерете корена на уравнението. Ако има няколко корена, посочете по-малкия в отговора си.

Решение:

Първо, нека напишем ODZ:

Сега си спомняме какво е логаритъм: до каква степен трябва да повишите основата, за да получите аргумент? Във втория. Това е:

Изглежда, че по-малкият корен е равен. Но това не е така: според ODZ коренът е на трета страна, тоест изобщо не е коренът на това уравнение. Следователно уравнението има само един корен: .

Отговор: .

Основна логаритмична идентичност

Припомнете си дефиницията на логаритъм в общи линии:

Заместете във второто равенство вместо логаритъма:

Това равенство се нарича основна логаритмична идентичност. Въпреки че по същество това равенство е просто написано по различен начин дефиниция на логаритъма:

Това е силата, до която трябва да се повишите, за да стигнете.

Например:

Решете следните примери:

Пример 2

Намерете стойността на израза.

Решение:

Припомнете си правилото от раздела:, тоест при повишаване на степен на степен показателите се умножават. Нека го приложим:

Пример 3

Докажи това.

Решение:

Свойства на логаритмите

За съжаление задачите не винаги са толкова прости - често първо трябва да опростите израза, да го приведете в обичайната форма и едва тогава ще бъде възможно да се изчисли стойността. Най-лесно е да направите това, знаейки свойства на логаритмите. Така че нека научим основните свойства на логаритмите. Ще докажа всеки един от тях, защото всяко правило се запомня по-лесно, ако знаете откъде идва.

Всички тези свойства трябва да се запомнят; без тях повечето проблеми с логаритмите не могат да бъдат решени.

И сега за всички свойства на логаритмите по-подробно.

Свойство 1:

доказателство:

Нека тогава.

Имаме: , h.t.d.

Свойство 2: Сума от логаритми

Сборът от логаритми със същата основа е равен на логаритъма на произведението: .

доказателство:

Нека тогава. Нека тогава.

пример:Намерете стойността на израза: .

Решение: .

Формулата, която току-що научихте, помага да се опрости сумата от логаритмите, а не разликата, така че тези логаритми не могат да бъдат комбинирани веднага. Но можете да направите обратното - "разбийте" първия логаритъм на две: И ето обещаното опростяване:
.
Защо е необходимо това? Е, например: какво значение има?

Сега е очевидно, че.

Сега улесни го за себе си:

задачи:

Отговори:

Свойство 3: Разлика на логаритмите:

доказателство:

Всичко е точно както в параграф 2:

Нека тогава.

Нека тогава. Ние имаме:

Примерът от последната точка вече е още по-прост:

По-сложен пример: . Познайте сами как да решите?

Тук трябва да се отбележи, че нямаме нито една формула за логаритмите на квадрат. Това е нещо подобно на израз - това не може да бъде опростено веднага.

Затова нека се отклоним от формулите за логаритмите и да помислим какви формули обикновено използваме в математиката най-често? Още от 7 клас!

То - . Трябва да свикнеш с факта, че те са навсякъде! И в експоненциални, и в тригонометрични, и в ирационални задачи, те се намират. Следователно те трябва да бъдат запомнени.

Ако се вгледате внимателно в първите два термина, става ясно, че това е така разлика на квадратите:

Отговорете за проверка:

Опростете се.

Примери

Отговори.

Свойство 4: Извличане на експонента от аргумента на логаритъма:

доказателство:И тук използваме и определението на логаритъма: нека, тогава. Имаме: , h.t.d.

Можете да разберете това правило по следния начин:

Тоест степента на аргумента се взема напред от логаритъма като коефициент.

пример:Намерете стойността на израза.

Решение: .

Решете сами:

Примери:

Отговори:

Свойство 5: Извличане на степента от основата на логаритъма:

доказателство:Нека тогава.

Имаме: , h.t.d.
Запомнете: от основаниястепен се представя като обратенномер, за разлика от предишния случай!

Свойство 6: Извличане на степента от основата и аргумента на логаритъма:

Или ако градусите са еднакви: .

Свойство 7: Преход към нова база:

доказателство:Нека тогава.

Имаме: , h.t.d.

Свойство 8: Размяна на основата и аргумента на логаритъма:

доказателство:Това е специален случай на формула 7: ако заменим, получаваме: , p.t.d.

Нека разгледаме още няколко примера.

Пример 4

Намерете стойността на израза.

Използваме свойството на логаритми No2 - сборът от логаритми със същата основа е равен на логаритъма на произведението:

Пример 5

Намерете стойността на израза.

Решение:

Използваме свойството на логаритми № 3 и № 4:

Пример 6

Намерете стойността на израза.

Решение:

Използвайки имот номер 7 - отидете на база 2:

Пример 7

Намерете стойността на израза.

Решение:

Как ви харесва статията?

Ако четете тези редове, значи сте прочели цялата статия.

И е готино!

А сега ни кажете как ви харесва статията?

Научихте ли се да решавате логаритми? Ако не, какъв е проблемът?

Пишете ни в коментарите по-долу.

И да, успех с изпитите.

На Единния държавен изпит и ОГЕ и изобщо в живота

логаритъм положително число N към основата(б> 0, б 1 ) се нарича експонентах , до който трябва да повишите b, за да получите N .

Логаритъм нотация:

Този запис е еквивалентен на следното:b x = N .

ПРИМЕРИ: дневник 3 81 = 4, тъй като 3 4 \u003d 81;

Дневник 1/3 27 = – 3 , тъй като (1/3) - 3 = 3 3 = 27 .

Горното определение на логаритъма може да бъде записано като идентичност:

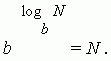
Основни свойства на логаритмите.

1) дневник б= 1 , защото б 1 = b.

б

2) дневник 1 = 0 , защото б 0 = 1 .

б

3) Логаритъмът на произведението е равен на сбора от логаритмите на факторите:

дневник( аб) = дневник а+дневник б.

4) Логаритъмът на частното е равен на разликата между логаритмите на дивидента и делителя:

дневник( а/б) = дневник а– дневник б.

5) Логаритъмът на степента е равен на произведението на експонента и логаритъма на неговата основа:

дневник (б к ) = кдневник б.

Последствието от това свойство е следното:лог корен равен на логаритъма на коренното число, разделен на степента на корена:

6) Ако основата на логаритъма е степен, тогава стойността реципрочната стойност на степента може да бъде извадена от знака на дневникарима:

Последните две свойства могат да бъдат комбинирани в едно:

7) Формула за преходен модул (т.е.д . преход от една базалогаритъм към друга основа):

В конкретен случай, когато N = ание имаме:

Десетичен логаритъм Наречен основен логаритъм 10. Посочено е lg , т.е. дневник 10 н = lg н. Логаритми от числа 10, 100, 1000, ...стр са съответно 1, 2, 3, …,тези. има толкова много положителни

единици, колко нули са в логаритъма след единица. Логаритми от числа 0,1, 0,01, 0,001, ...стр avny съответно –1, –2, –3, …, т.е. има толкова отрицателни единици, колкото има нули в числото на логаритъма преди единицата ( броене и нула цели числа). Логаритми други числа имат дробна част, наречена мантиса. Цялачаст от логаритъма се нарича Характеристика. За практическидесетичните логаритми са най-удобни.

естествен логаритъм Наречен основен логаритъм д. Обозначава сеВ , т.е. дневник дн = вътре н. номер де ирационално,приблизителната стойност е 2,718281828.То е границата, към която клони числото(1 + 1 / н) н с неограничено увеличениен(см. първата чудесна граница ).
Колкото и странно да изглежда, естествените логаритми се оказаха много удобни при извършване на различни операции, свързани с анализа на функциите.Изчисляване на основни логаритмидмного по-бързо от всяка друга основа.

И така, имаме правомощия по две. Ако вземете числото от долния ред, тогава лесно можете да намерите степента, до която трябва да вдигнете двойка, за да получите това число. Например, за да получите 16, трябва да повишите две на четвърта степен. И за да получите 64, трябва да вдигнете две на шеста степен. Това се вижда от таблицата.

И сега - всъщност дефиницията на логаритъма:

Основният логаритъм на аргумента x е степента, до която трябва да се повдигне числото a, за да се получи числото x.

Нотация: log a x \u003d b, където a е основата, x е аргументът, b всъщност е равен на логаритъма.

Например, 2 3 = 8 ⇒ log 2 8 = 3 (основният 2 логаритъм на 8 е три, защото 2 3 = 8). Може също да се регистрира 2 64 = 6, защото 2 6 = 64.

Операцията за намиране на логаритъм на число спрямо дадена основа се нарича логаритъм. Така че нека добавим нов ред към нашата таблица:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

За съжаление, не всички логаритми се разглеждат толкова лесно. Например, опитайте се да намерите log 2 5. Числото 5 не е в таблицата, но логиката диктува, че логаритъмът ще лежи някъде в сегмента. Защото 22< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Такива числа се наричат ​​ирационални: числата след десетичната запетая могат да се записват за неопределено време и никога не се повтарят. Ако логаритъмът се окаже ирационален, по-добре е да го оставите така: log 2 5, log 3 8, log 5 100.

Важно е да се разбере, че логаритъмът е израз с две променливи (база и аргумент). В началото много хора бъркат къде е основата и къде е аргументът. За да избегнете досадни недоразумения, просто погледнете снимката:

Пред нас не е нищо повече от определението на логаритъма. Помня: логаритъмът е степента, към което трябва да повдигнете основата, за да получите аргумента. Именно основата е издигната до степен - на снимката е подчертана в червено. Оказва се, че основата винаги е отдолу! Казвам това прекрасно правило на моите ученици още на първия урок - и няма объркване.

Разбрахме определението - остава да се научим как да броим логаритми, т.е. отървете се от знака "дневник". Като начало отбелязваме, че от определението следват два важни факта:

1. Аргументът и основата трябва винаги да са по-големи от нула. Това следва от дефиницията на степента чрез рационален показател, до който се свежда определението на логаритъма.
2. Основата трябва да е различна от единица, тъй като единица за всяка степен все още е единица. Поради това въпросът „до каква степен трябва да се издигне човек, за да се получат две“ е безсмислен. Няма такава степен!

Такива ограничения се наричат валиден диапазон(ODZ). Оказва се, че ODZ на логаритъма изглежда така: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Имайте предвид, че няма ограничения за числото b (стойността на логаритъма) не се налага. Например, логаритъмът може да бъде отрицателен: log 2 0,5 = −1, тъй като 0,5 = 2 −1 .

Сега обаче разглеждаме само числови изрази, при които не се изисква да се знае ODZ на логаритъма. Всички ограничения вече са взети предвид от съставителите на проблемите. Но когато логаритмичните уравнения и неравенства влязат в игра, изискванията на DHS ще станат задължителни. Всъщност в основата и аргумента може да има много силни конструкции, които не отговарят непременно на горните ограничения.

Сега разгледайте общата схема за изчисляване на логаритми. Състои се от три стъпки:

1. Изразете основата a и аргумента x като степен с най-малката възможна основа, по-голяма от единица. По пътя е по-добре да се отървете от десетичните дроби;
2. Решете уравнението за променливата b: x = a b ;
3. Полученото число b ще бъде отговорът.

Това е всичко! Ако логаритъмът се окаже ирационален, това ще се види още на първата стъпка. Изискването основата да е по-голяма от единица е много актуално: това намалява вероятността от грешка и значително опростява изчисленията. Аналогично и с десетичните дроби: ако веднага ги преобразувате в обикновени, ще има много пъти по-малко грешки.

Нека видим как работи тази схема с конкретни примери:

Задача. Изчислете логаритъма: log 5 25

1. Нека представим основата и аргумента като степен на пет: 5 = 5 1 ; 25 = 52;
2. Нека направим и решим уравнението:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. Получих отговор: 2.

Задача. Изчислете логаритъма:

Задача. Изчислете логаритъма: log 4 64

1. Нека представим основата и аргумента като степен на две: 4 = 2 2 ; 64 = 26;
2. Нека направим и решим уравнението:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. Получих отговор: 3.

Задача. Изчислете логаритъма: log 16 1

1. Нека представим основата и аргумента като степен на две: 16 = 2 4 ; 1 = 20;
2. Нека направим и решим уравнението:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. Получен отговор: 0.

Задача. Изчислете логаритъма: log 7 14

1. Нека представим основата и аргумента като степен на седем: 7 = 7 1 ; 14 не е представено като степен на седем, защото 7 1< 14 < 7 2 ;
2. От предходния параграф следва, че логаритъмът не се взема предвид;
3. Отговорът е без промяна: дневник 7 14.

Малка забележка за последния пример. Как да се уверите, че едно число не е точна степен на друго число? Много просто - просто го разложете на прости фактори. И ако такива фактори не могат да бъдат събрани в степен със същите показатели, тогава първоначалното число не е точна степен.

Задача. Разберете дали точните степени на числото са: 8; 48; 81; 35; четиринадесет.

8 \u003d 2 2 2 \u003d 2 3 е точната степен, тъй като има само един множител;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 не е точна степен, защото има два фактора: 3 и 2;
81 \u003d 9 9 \u003d 3 3 3 3 = 3 4 - точна степен;
35 \u003d 7 5 - отново не точна степен;
14 \u003d 7 2 - отново не е точна степен;

Забележете също, че самите прости числа винаги са точни степени на самите себе си.

Десетичен логаритъм

Някои логаритми са толкова често срещани, че имат специално име и обозначение.

Десетичният логаритъм на аргумента x е логаритъмът с основа 10, т.е. степента, до която трябва да повишите числото 10, за да получите числото x. Обозначение: lg x .

Например, log 10 = 1; log 100 = 2; lg 1000 = 3 - и т.н.

Оттук нататък, когато в учебника се появи фраза като „Намери lg 0.01“, знайте, че това не е печатна грешка. Това е десетичният логаритъм. Ако обаче не сте свикнали с такова обозначение, винаги можете да го пренапишете:
log x = log 10 x

Всичко, което е вярно за обикновените логаритми, е вярно и за десетичните.

естествен логаритъм

Има и друг логаритъм, който има собствено обозначение. В известен смисъл тя е дори по-важна от десетичната. Това е естественият логаритъм.

Естественият логаритъм на аргумента x е логаритъмът към основата e , т.е. степента, до която трябва да се повиши числото e, за да се получи числото x. Обозначение: ln x .

Мнозина ще попитат: какво друго е числото e? Това е ирационално число, точната му стойност не може да се намери и запише. Ето само първите числа:
e = 2,718281828459...

Няма да задълбаваме какво представлява този номер и защо е необходим. Само не забравяйте, че e е основата на естествения логаритъм:
ln x = log e x

Така ln e = 1; log e 2 = 2; ln e 16 = 16 - и т.н. От друга страна, ln 2 е ирационално число. По принцип естественият логаритъм на всяко рационално число е ирационален. Освен, разбира се, единство: ln 1 = 0.

За естествените логаритми са валидни всички правила, които са верни за обикновените логаритми.

Дадени са основните свойства на естествения логаритъм, графика, област на дефиниране, набор от стойности, основни формули, производна, интеграл, разлагане в степенен ред и представяне на функцията ln x посредством комплексни числа.

Съдържание

Обратна функция

Реципрочната стойност за естествения логаритъм е изложител.

Ако, тогава

Ако , тогава .

Производна ln x

Производна на естествения логаритъм:
.
Производна на естествения логаритъм на модул x:
.
Производна от n-ти ред:
.
Извеждане на формули >>>

Интегрална

Изчислява се интегралът интегриране по части :
.
Така,

Изрази по отношение на комплексни числа

Помислете за функция на комплексна променлива z :
.
Нека изразим комплексната променлива zчрез модул rи аргумент φ :
.
Използвайки свойствата на логаритъма, имаме:
.
Или
.
Аргументът φ не е еднозначно дефиниран. Ако поставим
, където n е цяло число,
тогава ще бъде едно и също число за различни n.

Следователно, естественият логаритъм, като функция на комплексна променлива, не е еднозначна функция.

Разширяване на силовата серия

За , разширяването се извършва:

Препратки:
И.Н. Бронщайн, К.А. Семендяев, Наръчник по математика за инженери и студенти от висши учебни заведения, Lan, 2009.

Вижте също: