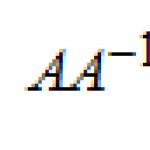Решение на експоненциални уравнения. Примери.
Внимание!
Има допълнителни
материал в специален раздел 555.
За тези, които силно "не много..."
И за тези, които "много...")
Какво експоненциално уравнение? Това е уравнение, в което са неизвестните (x) и изразите с тях индикаторинякои степени. И само там! Важно е.
Ето къде си примери за експоненциални уравнения:
3 x 2 x = 8 x + 3
Забележка! В основите на градусите (по-долу) - само числа. AT индикаториградуси (по-горе) - голямо разнообразие от изрази с x. Ако изведнъж в уравнението се появи x някъде, различно от индикатора, например:
това ще бъде уравнение от смесен тип. Такива уравнения нямат ясни правила за решаване. Засега няма да ги разглеждаме. Тук ще се справим с решение на експоненциални уравненияв най-чистата си форма.
Всъщност дори чистите експоненциални уравнения не винаги са ясно решени. Но има определени видове експоненциални уравнения, които могат и трябва да бъдат решени. Това са видовете, които ще разгледаме.
Решение на най-простите експоненциални уравнения.
Нека започнем с нещо много основно. Например:
Дори и без никаква теория, чрез проста селекция става ясно, че x = 2. Нищо повече, нали!? Няма други хвърлини стойности. И сега нека разгледаме решението на това сложно експоненциално уравнение:
какво сме направили? Ние всъщност просто изхвърлихме едни и същи дъна (тройки). Напълно изхвърлен. И това, което радва, уцели целта!
Наистина, ако в експоненциалното уравнение отляво и отдясно са същоточисла във всяка степен, тези числа могат да бъдат премахнати и равни експоненти. Математиката позволява. Остава да се реши много по-просто уравнение. Хубаво е, нали?)
Все пак нека си припомним иронично: можете да премахнете базите само когато базовите номера отляво и отдясно са в страхотна изолация!Без никакви съседи и коефициенти. Да кажем в уравненията:
2 x +2 x + 1 = 2 3 , или
Не можете да премахнете двойници!
Е, усвоихме най-важното. Как да преминем от лоши експоненциални изрази към по-прости уравнения.
— Ето ги тези времена! - ти каза. "Кой ще даде такъв примитив на контролни и изпити!?"
Принуден да се съгласи. Никой няма. Но сега знаете къде да отидете, когато решавате объркващи примери. Необходимо е да го напомним, когато едно и също базово число е отляво - отдясно. Тогава всичко ще бъде по-лесно. Всъщност това е класиката на математиката. Вземаме оригиналния пример и го трансформираме в желаното насум. По правилата на математиката, разбира се.
Помислете за примери, които изискват някои допълнителни усилия, за да ги доведете до най-простите. Да им се обадим прости експоненциални уравнения.
Решение на прости експоненциални уравнения. Примери.
При решаване на експоненциални уравнения основните правила са действия с правомощия.Без познаване на тези действия нищо няма да работи.
Към действията с степени трябва да се добави лично наблюдение и изобретателност. Имаме ли нужда от еднакви основни числа? Така че ние ги търсим в примера в изрична или криптирана форма.
Да видим как се прави това на практика?
Нека ни дадем пример:
2 2x - 8 x+1 = 0
Първи поглед към основания.Те... Различни са! Две и осем. Но е твърде рано да се обезкуражаваме. Време е да си спомним това
Двама и осем са роднини по степен.) Напълно възможно е да се запише:
8 x+1 = (2 3) x+1
Ако си припомним формулата от действия с правомощия:
(a n) m = a nm ,
като цяло работи страхотно:
8 x+1 = (2 3) x+1 = 2 3(x+1)
Оригиналният пример изглежда така:
2 2x - 2 3(x+1) = 0
Прехвърляме 2 3 (x+1)вдясно (никой не е отменил елементарните действия на математиката!), получаваме:
2 2x \u003d 2 3 (x + 1)
Това е практически всичко. Премахване на основи:
Решаваме това чудовище и получаваме
Това е правилният отговор.
В този пример познаването на силите на две ни помогна. ние идентифициранв осмицата, криптираната двойка. Тази техника (кодиране на общи бази под различни числа) е много популярен трик в експоненциалните уравнения! Да, дори в логаритми. Човек трябва да може да разпознава степените на други числа в числа. Това е изключително важно за решаването на експоненциални уравнения.
Факт е, че вдигането на произволно число на всяка степен не е проблем. Умножете, дори на лист хартия, и това е всичко. Например всеки може да вдигне 3 на пета степен. 243 ще се окаже, ако знаете таблицата за умножение.) Но в експоненциалните уравнения много по-често е необходимо да не се повишава на степен, а обратното ... какъв номер до каква степенсе крие зад числото 243 или, да речем, 343... Никой калкулатор няма да ви помогне тук.
Трябва да знаеш силите на някои числа наглед, да... Да се упражняваме ли?
Определете какви степени и какви числа са числа:
2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729, 1024.
Отговори (в бъркотия, разбира се!):
5 4 ; 2 10 ; 7 3 ; 3 5 ; 2 7 ; 10 2 ; 2 6 ; 3 3 ; 2 3 ; 2 1 ; 3 6 ; 2 9 ; 2 8 ; 6 3 ; 5 3 ; 3 4 ; 2 5 ; 4 4 ; 4 2 ; 2 3 ; 9 3 ; 4 5 ; 8 2 ; 4 3 ; 8 3 .
Ако се вгледате внимателно, можете да видите странен факт. Има повече отговори, отколкото въпроси! Е, случва се... Например 2 6 , 4 3 , 8 2 е всичко 64.
Да приемем, че сте си взели под внимание информацията за запознаване с числата.) Нека ви напомня също, че за решаване на експоненциални уравнения прилагаме цялотозапас от математически знания. Включително от долните средни класове. Не си отишъл направо в гимназията, нали?
Например, когато решавате експоненциални уравнения, поставянето на общия множител извън скоби много често помага (здравейте на 7-ми клас!). Да видим пример:
3 2x+4 -11 9 x = 210
И отново, първият поглед - на основание! Основите на степените са различни... Три и девет. И ние искаме те да бъдат същите. Е, в този случай желанието е напълно осъществимо!) Защото::
9 x = (3 2) x = 3 2x
По същите правила за действия със степени:
3 2x+4 = 3 2x 3 4
Това е страхотно, можете да напишете:
3 2x 3 4 - 11 3 2x = 210
Дадохме пример по същите причини. И така, какво следва!? Тройки не могат да се изхвърлят ... Безизходица?
Въобще не. Запомнете най-универсалното и мощно правило за вземане на решения всичкоматематически задачи:
Ако не знаете какво да правите, направете каквото можете!
Гледаш, всичко се оформя).
Какво има в това експоненциално уравнение могаправя? Да, лявата страна директно пита за скоби! Общият фактор 3 2x ясно загатва за това. Нека опитаме и тогава ще видим:
3 2x (3 4 - 11) = 210
3 4 - 11 = 81 - 11 = 70
Примерът става все по-добър и по-добър!
Припомняме, че за да премахнем основите, се нуждаем от чиста степен, без никакви коефициенти. Числото 70 ни притеснява. И така, разделяме двете страни на уравнението на 70, получаваме:
Оп-па! Всичко е било наред!
Това е окончателният отговор.
Случва се обаче да се получи рулиране на същото основание, но не и тяхното ликвидиране. Това се случва в експоненциални уравнения от друг тип. Да вземем този тип.
Промяна на променлива при решаване на експоненциални уравнения. Примери.
Нека решим уравнението:
4 x - 3 2 x +2 = 0
Първо - както обикновено. Да преминем към основата. Към двойката.
4 x = (2 2) x = 2 2x
Получаваме уравнението:
2 2x - 3 2 x +2 = 0
И тук ще висим. Предишните трикове няма да работят, както и да го завъртите. Ще трябва да вземем от арсенала на друг мощен и гъвкав начин. Нарича се променлива замяна.
Същността на метода е изненадващо проста. Вместо една сложна икона (в нашия случай 2 x), пишем друга, по-проста (например t). Такава привидно безсмислена замяна води до невероятни резултати!) Всичко просто става ясно и разбираемо!
Така че нека
Тогава 2 2x = 2 x2 = (2 x) 2 = t 2
Заменяме в нашето уравнение всички степени с x с t:
Е, светва ли?) Още ли не сте забравили квадратните уравнения? Решаваме чрез дискриминанта, получаваме:
Тук основното е да не спираме, както се случва ... Това все още не е отговорът, имаме нужда от x, а не t. Връщаме се към Xs, т.е. извършване на подмяна. Първо за t 1:
Това е,
Един корен беше намерен. Търсим втория, от t 2:
Хм... Ляво 2 х, Дясно 1... Закачване? Да, изобщо не! Достатъчно е да запомните (от действия със степени, да ...), че е единство всякаквичисло до нула. Всякакви. Каквото ви трябва, ние ще го поставим. Трябва ни двойка. означава:
Това е всичко. Имам 2 корена:
Това е отговорът.
В решаване на експоненциални уравнениянакрая понякога се получава някакъв неудобен израз. Тип:
От седемте, двойка до проста степен не работи. Те не са роднини... Как мога да бъда тук? Някой може да се обърка ... Но човекът, който прочете на този сайт темата "Какво е логаритъм?" , само се усмихнете пестеливо и запишете с твърда ръка абсолютно верния отговор:
Не може да има такъв отговор в задачи "Б" на изпита. Изисква се конкретен номер. Но в задачи "C" - лесно.
Този урок предоставя примери за решаване на най-често срещаните експоненциални уравнения. Нека подчертаем основното.
Практически съвети:
1. На първо място, ние разглеждаме основанияградуси. Да видим дали не могат да се направят същото.Нека се опитаме да направим това чрез активно използване действия с правомощия.Не забравяйте, че числата без x също могат да се превърнат в степени!
2. Опитваме се да приведем експоненциалното уравнение до вида, когато лявото и дясното са същоточисла до всякаква степен. Ние използваме действия с правомощияи факторизация.Това, което може да се брои в числа - ние броим.
3. Ако вторият съвет не работи, се опитваме да приложим заместването на променливата. Резултатът може да бъде уравнение, което лесно се решава. Най-често - квадрат. Или дробно, което също се свежда до квадрат.
4. За да решавате успешно експоненциални уравнения, трябва да знаете степените на някои числа „на очи“.
Както обикновено, в края на урока сте поканени да решите малко.) Сами. От просто към сложно.
Решете експоненциални уравнения:
По-трудно:
2 x + 3 - 2 x + 2 - 2 x \u003d 48
9 x - 8 3 x = 9
2 x - 2 0,5 x + 1 - 8 = 0
Намерете произведение на корените:
2 3-x + 2 x = 9
Се случи?
Е, тогава най-сложният пример (решен е обаче в ума...):
7 0,13x + 13 0,7x+1 + 2 0,5x+1 = -3
Какво е по-интересно? Тогава ето лош пример за вас. Доста издърпващо при повишена трудност. Ще намекна, че в този пример изобретателността и най-универсалното правило за решаване на всички математически задачи спестяват.)
2 5x-1 3 3x-1 5 2x-1 = 720 x
Примерът е по-прост, за релаксация):
9 2 x - 4 3 x = 0
И за десерт. Намерете сумата от корените на уравнението:
x 3 x - 9x + 7 3 x - 63 = 0
Да да! Това е уравнение от смесен тип! Което не разгледахме в този урок. И какво да ги разгледаме, те трябва да бъдат решени!) Този урок е напълно достатъчен за решаване на уравнението. Е, нужна е изобретателност... И да, седми клас ще ви помогне (това е намек!).
Отговори (в безпорядък, разделени с точка и запетая):
един; 2; 3; четири; няма решения; 2; -2; -5; четири; 0
Всичко успешно ли е? Отлично.
Има проблем? Няма проблем! В специален раздел 555 всички тези експоненциални уравнения се решават с подробни обяснения. Какво, защо и защо. И, разбира се, има допълнителна ценна информация за работата с всякакви експоненциални уравнения. Не само с тези.)
Един последен забавен въпрос за разглеждане. В този урок работихме с експоненциални уравнения. Защо не казах и дума за ОДЗ тук?В уравненията това е много важно нещо, между другото ...
Ако харесвате този сайт...
Между другото, имам още няколко интересни сайта за вас.)
Можете да практикувате решаването на примери и да разберете нивото си. Тестване с незабавна проверка. Учене - с интерес!)
можете да се запознаете с функции и производни.









 Назад напред
Назад напред
Внимание! Предварителният преглед на слайда е само за информационни цели и може да не представлява пълния обхват на презентацията. Ако се интересувате от тази работа, моля, изтеглете пълната версия.
Тип урок
: урок за обобщаване и комплексно прилагане на знания, умения и умения на тема „Експоненциални уравнения и начини за тяхното решаване”.Цели на урока.
Оборудване:
компютър и мултимедиен проектор.Урокът използва Информационни технологии : методическа подкрепа на урока - презентация в Microsoft Power Point.
По време на занятията
Всяко умение идва с упорита работа.
аз Поставяне на целта на урока(слайд номер 2 )
В този урок ще обобщим и обобщим темата „Експоненциални уравнения, техните решения“. Нека се запознаем с типичните задачи на изпита от различни години по тази тема.
Задачите за решаване на експоненциални уравнения могат да бъдат намерени във всяка част от задачите на USE. В частта " В " обикновено предлагат да се решат най-простите експоненциални уравнения. В частта " ОТ " можете да срещнете по-сложни експоненциални уравнения, чието решение обикновено е един от етапите на задачата.
Например ( слайд номер 3 ).
- ИЗПОЛЗВАНЕ - 2007г
B 4 - Намерете най-голямата стойност на израза x y, където ( Х; при) е решението на системата:

B 1 - Решаване на уравнения:
а) х 6 3х – 36 6 3х = 0;
б) 4 х +1 + 8 4х= 3.
B 4 - Намерете стойността на израза х + у, където ( Х; при) е решението на системата:

- ИЗПОЛЗВАНЕ - 2010г

II. Актуализиране на основни знания. Повторение
(Слайдове № 4 – 6 презентации в клас)Показва се екранът справочно резюме на теоретичния материал по тази тема.
Обсъждат се следните въпроси:
- Как се наричат уравнения показателен?
- Назовете основните начини за решаването им. Дайте примери за техните видове ( слайд номер 4 )
- Каква теорема се използва за решаване на най-простите експоненциални уравнения от вида: и f(x) = a g(x) ?
- Какви други методи за решаване на експоненциални уравнения съществуват? ( слайд номер 5 )
(Решете сами предложените уравнения за всеки метод и извършете самотест с помощта на слайда)
- Метод на факторизация (въз основа на свойствата на мощностите с същите основи, приемане: степента с най-нисък индикатор се изважда от скоби).
- Получаване на деление (умножение) чрез експоненциален израз, различен от нула, при решаване на хомогенни експоненциални уравнения .
- съвет:
-
Решаване на уравнения с последните два метода, последвано от коментари
(слайд номер 6 ).
. 4 х+ 1 – 2 4 х– 2 = 124, 4 х– 2 (4 3 - 2) = 124, 4 х– 2 62 = 124,4 х– 2 = 2, 4 х– 2 = 4 0,5 , х– 2 = 0,5, х = 2,5 .
2 2 2x – 3 2 х 5Х - 5 5 2х= 0¦: 5 2 х 0,2 (2/5) 2x - 3 (2/5) Х - 5 = 0,
t = (2/5) x, T > 0, 2T 2 - 3T- 5 = 0,T= -1(?...), t = 5/2; 5/2 = (2/5) x, х= ?...
III. Решаване на USE задачи 2010
Учениците решават самостоятелно задачите, предложени в началото на урока на слайд № 3, като използват инструкциите за решението, проверяват процеса на вземане на решение и отговорите им с помощта на презентацията ( слайд номер 7). В процеса на работа се обсъждат варианти и методи за решаване, обръща се внимание на възможни грешки в решението.
: а) 7 х– 2 = 49, б) (1/6) 12 - 7 х = 36. Отговор: а) х= 4, б) х = 2. : 4 х 2 + 3х – 2 - 0,5 2x2 + 2х- 1 = 0. (Можете да замените 0,5 \u003d 4 - 0,5)Решение. ,
х 2 + 3х – 2 = -х 2 - 4х + 0,5 …
Отговор: х= -5/2, х = 1/2.
: 5 5 tg г+ 4 = 5 -tg г, при cos г< 0.Предложение за решение
. 5 5 tg г+ 4 = 5 -tg г¦ 5 tg г 0,5 5 2 г г+ 4 5 tg y- 1 = 0. Нека х= 5 tg г , …
5 tg г = -1 (?...), 5 tg y= 1/5.
Тъй като тг г= -1 и cos г< 0, тогава при II координатен квартал
Отговор: при= 3/4 + 2к, к н.
IV. Сътрудничество с бяла дъска
Задачата за високо ниво на обучение се счита - слайд номер 8. С помощта на този слайд се осъществява диалог между учител и ученици, което допринася за разработването на решението.
- При какъв параметър а уравнение 2 2 х – 3 2 х + а 2 – 4а= 0 има два корена?Позволявам T= 2 х, където T > 0 . Получаваме T 2 – 3T + (а 2 – 4а) = 0 .
едно). Тъй като уравнението има два корена, то D > 0;
2). Защото T 1,2 > 0, тогава T 1 T 2 > 0, т.е а 2 – 4а> 0 (?...).

Отговор: а(– 0,5; 0) или (4; 4,5).
V. Проверка
(слайд номер 9 )Учениците изпълняват верификационна работавърху листовки, упражнявайки самоконтрол и самооценка на извършената работа с помощта на презентация, утвърждаваща се в темата. Те самостоятелно определят за себе си програма за регулиране и коригиране на знания въз основа на грешки, направени в работните тетрадки. Листове с изпълнена самостоятелна работа се предават на учителя за проверка.
Подчертаните числа са основни, тези със звездичка са напреднали.

Решение и отговори.
3. 2 х– 1 (5 2 4 - 4) = 19, 2 х– 1 76 = 19, 2 х– 1 = 1/4, 2 х– 1 = 2 – 2 , х– 1 = -2,
х = -1.
4 *.3 9 x = 2 3 х 5х+ 5 25 х | : 25 х ,
3 (9/25) x = 2 (3/5) х+ 5,
3 (9/27) х = 2 (3/5) х + 5 = 0,
3 (3/5) 2х – 2 (3/5) х - 5 = 0,…, (3/5) х = -1 (неподходящ),
(3/5) х = 5, х = -1.
VI. Домашна работа
(слайд номер 10 )- Повторете § 11, 12.
- От материалите на Единния държавен изпит 2008 - 2010 г. изберете задачи по темата и ги решете.
- Домашна тестова работа :

Този урок е предназначен за тези, които тепърва започват да учат експоненциални уравнения. Както винаги, нека започнем с определение и прости примери.
Ако четете този урок, тогава подозирам, че вече имате поне минимално разбиране на най-простите уравнения – линейни и квадратни: $56x-11=0$; $((x)^(2))+5x+4=0$; $((x)^(2))-12x+32=0$ и т.н. Решаването на подобни конструкции е абсолютно необходимо, за да не се „виси“ в темата, която ще бъде обсъдена сега.
И така, експоненциални уравнения. Нека ви дам няколко примера:
\[((2)^(x))=4;\quad ((5)^(2x-3))=\frac(1)(25);\quad ((9)^(x))=- 3\]
Някои от тях може да ви се сторят по-сложни, някои от тях, напротив, са твърде прости. Но всички те са обединени от една важна характеристика: съдържат експоненциална функция $f\left(x \right)=((a)^(x))$. Така въвеждаме определението:
Експоненциално уравнение е всяко уравнение, което съдържа експоненциална функция, т.е. израз от формата $((a)^(x))$. В допълнение към посочената функция, такива уравнения могат да съдържат всякакви други алгебрични конструкции - полиноми, корени, тригонометрия, логаритми и др.
Добре тогава. Разбрах определението. Сега въпросът е: как да решим всички тези глупости? Отговорът е едновременно прост и сложен.
Нека започнем с добрата новина: от моя опит с много ученици мога да кажа, че за повечето от тях експоненциалните уравнения са много по-лесни от същите логаритми и още повече тригонометрията.
Но има и лоши новини: понякога съставителите на задачи за всякакви учебници и изпити са посещавани от „вдъхновение“ и техният възпален от наркотици мозък започва да произвежда толкова брутални уравнения, че става проблематично не само за студентите да ги решат - дори много учители се забиват в подобни проблеми.
Все пак да не говорим за тъжни неща. И нека се върнем към онези три уравнения, които бяха дадени в самото начало на историята. Нека се опитаме да решим всеки един от тях.
Първо уравнение: $((2)^(x))=4$. Е, до каква степен трябва да се повиши числото 2, за да се получи числото 4? Може би вторият? В крайна сметка, $((2)^(2))=2\cdot 2=4$ — и получихме правилното числово равенство, т.е. наистина $x=2$. Е, благодаря, шапка, но това уравнение беше толкова просто, че дори моята котка можеше да го реши. :)
Нека да разгледаме следното уравнение:
\[((5)^(2x-3))=\frac(1)(25)\]
Но тук е малко по-трудно. Много ученици знаят, че $((5)^(2))=25$ е таблицата за умножение. Някои също така подозират, че $((5)^(-1))=\frac(1)(5)$ по същество е дефиницията на отрицателни експоненти (подобно на формулата $((a)^(-n))= \ frac(1)(((a)^(n)))$).
И накрая, само няколко избрани предполагат, че тези факти могат да бъдат комбинирани и изходът е следният резултат:
\[\frac(1)(25)=\frac(1)(((5)^(2)))=((5)^(-2))\]
По този начин нашето първоначално уравнение ще бъде пренаписано, както следва:
\[((5)^(2x-3))=\frac(1)(25)\Стрелка надясно ((5)^(2x-3))=((5)^(-2))\]
И сега това вече е напълно решено! От лявата страна на уравнението има експоненциална функция, от дясната страна на уравнението има експоненциална функция, няма нищо друго освен тях никъде другаде. Следователно е възможно да се „изхвърлят“ основите и глупаво да се приравнят индикаторите:
Получихме най-простото линейно уравнение, което всеки ученик може да реши само с няколко реда. Добре, в четири реда:
\[\ начало(подравняване)& 2x-3=-2 \\& 2x=3-2 \\& 2x=1 \\& x=\frac(1)(2) \\\end(подравняване)\]
Ако не разбирате какво се случи в последните четири реда, не забравяйте да се върнете към темата „линейни уравнения“ и да я повторите. Защото без ясно усвояване на тази тема е твърде рано да се захващате с експоненциални уравнения.
\[((9)^(x))=-3\]
Е, как решаваш? Първа мисъл: $9=3\cdot 3=((3)^(2))$, така че оригиналното уравнение може да бъде пренаписано по следния начин:
\[((\ляво(((3)^(2)) \вдясно))^(x))=-3\]
След това припомняме, че при повишаване на степен в степен показателите се умножават:
\[((\left((3)^(2)) \right))^(x))=((3)^(2x))\Стрелка надясно ((3)^(2x))=-(( 3)^(1))\]
\[\начало(подравняване)& 2x=-1 \\& x=-\frac(1)(2) \\\end(подравняване)\]
И за такова решение получаваме честно заслужена двойка. Защото ние, с невъзмутимостта на покемон, изпратихме знака минус пред трите в силата на точно тази тройка. И не можете да направите това. И ето защо. Разгледайте различните сили на тройката:
\[\begin(matrix) ((3)^(1))=3& ((3)^(-1))=\frac(1)(3)& ((3)^(\frac(1)( 2)))=\sqrt(3) \\ ((3)^(2))=9& ((3)^(-2))=\frac(1)(9)& ((3)^(\ frac(1)(3)))=\sqrt(3) \\ ((3)^(3))=27& ((3)^(-3))=\frac(1)(27)& (( 3)^(-\frac(1)(2)))=\frac(1)(\sqrt(3)) \\\end(matrix)\]
Съставяйки тази таблетка, не се извратих веднага щом го направих: разгледах положителни степени и отрицателни, и дори дробни ... добре, къде е поне едно отрицателно число тук? Той не е! И не може да бъде, защото експоненциалната функция $y=((a)^(x))$, първо, винаги приема само положителни стойности (без значение колко умножите едно или разделите на две, тя пак ще бъде положително число), и второ, основата на такава функция, числото $a$, по дефиниция е положително число!
Е, как тогава да решим уравнението $((9)^(x))=-3$? Не, няма корени. И в този смисъл експоненциалните уравнения са много подобни на квадратните - също може да няма корени. Но ако в квадратните уравнения броят на корените се определя от дискриминанта (дискриминантът е положителен - 2 корена, отрицателен - няма корени), то в експоненциалните уравнения всичко зависи от това какво е вдясно от знака за равенство.
Така формулираме ключовия извод: най-простото експоненциално уравнение от вида $((a)^(x))=b$ има корен само ако $b \gt 0$. Знаейки този прост факт, можете лесно да определите дали предложеното ви уравнение има корени или не. Тези. струва ли си изобщо да го решаваш или веднага да запишеш, че няма корени.
Това знание ще ни помогне многократно, когато трябва да решаваме по-сложни проблеми. Междувременно достатъчно текстове - време е да проучим основния алгоритъм за решаване на експоненциални уравнения.
Как да решаваме експоненциални уравнения
И така, нека формулираме проблема. Необходимо е да се реши експоненциалното уравнение:
\[((a)^(x))=b,\quad a,b \gt 0\]
Според "наивния" алгоритъм, който използвахме по-рано, е необходимо да представим числото $b$ като степен на числото $a$:
Освен това, ако вместо променливата $x$ има някакъв израз, ще получим ново уравнение, което вече може да бъде решено. Например:
\[\begin(подравняване)& ((2)^(x))=8\Стрелка надясно ((2)^(x))=((2)^(3))\Стрелка надясно x=3; \\& ((3)^(-x))=81\Стрелка надясно ((3)^(-x))=((3)^(4))\Стрелка надясно -x=4\Стрелка надясно x=-4; \\& ((5)^(2x))=125\Стрелка надясно ((5)^(2x))=((5)^(3))\Стрелка надясно 2x=3\Стрелка надясно x=\frac(3)( 2). \\\край (подравняване)\]
И колкото и да е странно, тази схема работи в около 90% от случаите. Ами останалите 10% тогава? Останалите 10% са леко "шизофренични" експоненциални уравнения от вида:
\[((2)^(x))=3;\quad ((5)^(x))=15;\quad ((4)^(2x))=11\]
На каква степен трябва да вдигнете 2, за да получите 3? В първия? Но не: $((2)^(1))=2$ не е достатъчно. Във втория? Нито едно: $((2)^(2))=4$ е твърде много. Какво тогава?
Знаещите студенти вероятно вече са се досетили: в такива случаи, когато е невъзможно да се реши „красиво“, „тежка артилерия“ е свързана със случая - логаритми. Нека ви напомня, че с помощта на логаритми всяко положително число може да бъде представено като степен на всяко друго положително число (с изключение на едно):
Помните ли тази формула? Когато разказвам на учениците си за логаритмите, винаги ви предупреждавам: тази формула (тя е и основната логаритмична идентичност или, ако искате, дефиницията на логаритъма) ще ви преследва много дълго време и ще „изплува“ в най- неочаквани места. Е, тя изплува. Нека разгледаме нашето уравнение и тази формула:
\[\begin(подравняване)& ((2)^(x))=3 \\& a=((b)^(((\log )_(b))a)) \\\end(подравняване) \]
Ако приемем, че $a=3$ е нашето първоначално число вдясно, а $b=2$ е самата основа на експоненциалната функция, към която толкова искаме да намалим дясната страна, получаваме следното:
\[\begin(align)& a=((b)^((\log )_(b))a))\Стрелка надясно 3=((2)^((\log )_(2))3 )); \\& ((2)^(x))=3\Стрелка надясно ((2)^(x))=((2)^(((\log )_(2))3))\Стрелка надясно x=( (\log )_(2))3. \\\край (подравняване)\]
Получихме малко странен отговор: $x=((\log )_(2))3$. В някоя друга задача, с такъв отговор, мнозина биха се усъмнили и започнали да проверяват отново своето решение: ами ако някъде има грешка? Бързам да ви зарадвам: тук няма грешка, а логаритмите в корените на експоненциалните уравнения са доста типична ситуация. Така че свиквайте. :)
Сега решаваме по аналогия останалите две уравнения:
\[\begin(align)& ((5)^(x))=15\Стрелка надясно ((5)^(x))=((5)^(((\log )_(5))15)) \Стрелка надясно x=((\log )_(5))15; \\& ((4)^(2x))=11\Стрелка надясно ((4)^(2x))=((4)^(((\log )_(4))11))\Стрелка надясно 2x=( (\log )_(4))11\Стрелка надясно x=\frac(1)(2)((\log )_(4))11. \\\край (подравняване)\]
Това е всичко! Между другото, последният отговор може да бъде написан по различен начин:
Ние въведохме множителя в аргумента на логаритъма. Но никой не ни пречи да добавим този фактор към базата:
Освен това и трите варианта са правилни - те са просто различни форми на изписване на едно и също число. Кое да изберете и запишете в това решение зависи от вас.
Така се научихме да решаваме всякакви експоненциални уравнения от вида $((a)^(x))=b$, където числата $a$ и $b$ са строго положителни. Суровата реалност на нашия свят обаче е такава, че подобни прости задачи ще ви срещнат много, много рядко. По-често ще срещнете нещо подобно:
\[\begin(подравняване)& ((4)^(x))+((4)^(x-1))=((4)^(x+1))-11; \\& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2,7)^(1-x))=0,09. \\\край (подравняване)\]
Е, как решаваш? Може ли това изобщо да бъде разрешено? И ако да, как?
Без паника. Всички тези уравнения бързо и просто се свеждат до онези прости формули, които вече разгледахме. Просто трябва да знаете, за да запомните няколко трика от курса по алгебра. И разбира се, тук няма правила за работа с дипломи. Сега ще говоря за всичко това. :)
Преобразуване на експоненциални уравнения
Първото нещо, което трябва да запомните, е, че всяко експоненциално уравнение, колкото и сложно да е то, по един или друг начин трябва да се сведе до най-простите уравнения – точно тези, които вече разгледахме и които знаем как да решаваме. С други думи, схемата за решаване на всяко експоненциално уравнение е както следва:
- Запишете оригиналното уравнение. Например: $((4)^(x))+((4)^(x-1))=((4)^(x+1))-11$;
- Прави глупости. Или дори някакви глупости, наречени "преобразуване на уравнението";
- На изхода вземете най-простите изрази като $((4)^(x))=4$ или нещо друго подобно. Освен това едно първоначално уравнение може да даде няколко такива израза наведнъж.
С първата точка всичко е ясно - дори моята котка може да напише уравнението на лист. С третата точка също, изглежда, е повече или по-малко ясно - вече сме решили цял куп такива уравнения по-горе.
Но какво да кажем за втората точка? Какви са трансформациите? Какво да преобразувам в какво? И как?
Е, нека го разберем. Преди всичко бих искал да отбележа следното. Всички експоненциални уравнения са разделени на два вида:
- Уравнението е съставено от експоненциални функции със същата основа. Пример: $((4)^(x))+((4)^(x-1))=((4)^(x+1))-11$;
- Формулата съдържа експоненциални функции с различни бази. Примери: $((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x))$ и $((100)^(x-1) )\cdot ((2,7)^(1-x))=0,09$.
Нека започнем с уравнения от първия тип - те са най-лесни за решаване. И в тяхното решение ще ни помогне такава техника като подбора на стабилни изрази.
Подчертаване на стабилен израз
Нека отново да разгледаме това уравнение:
\[((4)^(x))+((4)^(x-1))=((4)^(x+1))-11\]
Какво виждаме? Четирите са повдигнати в различни степени. Но всички тези степени са прости суми от променливата $x$ с други числа. Ето защо е необходимо да запомните правилата за работа със степени:
\[\begin(подравняване)& ((a)^(x+y))=((a)^(x))\cdot ((a)^(y)); \\& ((a)^(x-y))=((a)^(x)):((a)^(y))=\frac(((a)^(x)))((a )^(y))). \\\край (подравняване)\]
Най-просто казано, събирането на степените може да се преобразува в продукт на степени, а изваждането лесно се преобразува в деление. Нека се опитаме да приложим тези формули към степените от нашето уравнение:
\[\begin(align)& ((4)^(x-1))=\frac(((4)^(x)))(((4)^(1)))=((4)^ (x))\cdot \frac(1)(4); \\& ((4)^(x+1))=((4)^(x))\cdot ((4)^(1))=((4)^(x))\cdot 4. \ \\край (подравняване)\]
Пренаписваме оригиналното уравнение, като вземем предвид този факт и след това събираме всички термини отляво:
\[\begin(align)& ((4)^(x))+((4)^(x))\cdot \frac(1)(4)=((4)^(x))\cdot 4 -единадесет; \\& ((4)^(x))+((4)^(x))\cdot \frac(1)(4)-((4)^(x))\cdot 4+11=0. \\\край (подравняване)\]
Първите четири термина съдържат елемента $((4)^(x))$ — нека го извадим от скобата:
\[\begin(align)& ((4)^(x))\cdot \left(1+\frac(1)(4)-4 \right)+11=0; \\& ((4)^(x))\cdot \frac(4+1-16)(4)+11=0; \\& ((4)^(x))\cdot \left(-\frac(11)(4) \right)=-11. \\\край (подравняване)\]
Остава да разделим двете части на уравнението на дроба $-\frac(11)(4)$, т.е. по същество умножете по обърнатата дроб - $-\frac(4)(11)$. Получаваме:
\[\begin(align)& ((4)^(x))\cdot \left(-\frac(11)(4) \right)\cdot \left(-\frac(4)(11) \right )=-11\cdot \left(-\frac(4)(11) \right); \\& ((4)^(x))=4; \\& ((4)^(x))=((4)^(1)); \\&x=1. \\\край (подравняване)\]
Това е всичко! Ние намалихме първоначалното уравнение до най-простото и получихме крайния отговор.
В същото време в процеса на решаване открихме (и дори извадихме от скобата) общия фактор $((4)^(x))$ - това е стабилният израз. Тя може да бъде обозначена като нова променлива или просто да я изразите точно и да получите отговор. Във всеки случай основният принцип на решението е следният:
Намерете в оригиналното уравнение стабилен израз, съдържащ променлива, която лесно се различава от всички експоненциални функции.
Добрата новина е, че почти всяко експоненциално уравнение допуска такъв стабилен израз.
Но има и лоши новини: подобни изрази могат да бъдат много трудни и може да бъде доста трудно да ги различим. Така че нека разгледаме друг проблем:
\[((5)^(x+2))+((0,2)^(-x-1))+4\cdot ((5)^(x+1))=2\]
Може би сега някой ще има въпрос: „Паша, убит ли си с камъни? Тук има различни бази - 5 и 0,2. Но нека се опитаме да преобразуваме мощност с база 0.2. Например, нека се отървем от десетичната дроб, като я доведем до обичайното:
\[((0,2)^(-x-1))=((0,2)^(-\left(x+1 \right)))=((\left(\frac(2)(10) ) \вдясно))^(-\left(x+1 \right)))=((\left(\frac(1)(5) \right))^(-\left(x+1 \right)) )\]
Както можете да видите, числото 5 все още се появи, макар и в знаменателя. В същото време индикаторът беше пренаписан като отрицателен. И сега си припомняме едно от най-важните правила за работа с степени:
\[((a)^(-n))=\frac(1)(((a)^(n)))\Стрелка надясно ((\left(\frac(1)(5) \right))^( -\left(x+1 \right)))=((\left(\frac(5)(1) \right))^(x+1))=((5)^(x+1))\ ]
Тук, разбира се, изневерих малко. Защото за пълно разбиране, формулата за премахване на отрицателните показатели трябваше да бъде написана, както следва:
\[((a)^(-n))=\frac(1)(((a)^(n)))=((\left(\frac(1)(a) \right))^(n ))\Стрелка надясно ((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=((\left(\frac(5)(1) \ вдясно))^(x+1))=((5)^(x+1))\]
От друга страна, нищо не ни попречи да работим само с една дроб:
\[((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=((\left((5)^(-1)) \ дясно))^(-\left(x+1 \right)))=((5)^(\left(-1 \right)\cdot \left(-\left(x+1 \right) \right) ))=((5)^(x+1))\]
Но в този случай трябва да можете да повишите степен до друга степен (напомням ви: в този случай показателите се сумират). Но не трябваше да „преобръщам“ дробите - може би за някой ще бъде по-лесно. :)
Във всеки случай, оригиналното експоненциално уравнение ще бъде пренаписано като:
\[\begin(подравняване)& ((5)^(x+2))+((5)^(x+1))+4\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+5\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(1))\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(x+2))=2; \\& 2\cdot ((5)^(x+2))=2; \\& ((5)^(x+2))=1. \\\край (подравняване)\]
Така се оказва, че първоначалното уравнение е дори по-лесно за решаване от разглежданото по-рано: тук дори не е нужно да отделяте стабилен израз - всичко е намалено от само себе си. Остава само да запомним, че $1=((5)^(0))$, откъдето получаваме:
\[\begin(подравняване)& ((5)^(x+2))=((5)^(0)); \\&x+2=0; \\&x=-2. \\\край (подравняване)\]
Това е цялото решение! Получихме окончателния отговор: $x=-2$. В същото време бих искал да отбележа един трик, който значително опрости всички изчисления за нас:
В експоненциалните уравнения не забравяйте да се отървете от десетичните дроби, да ги преведете в обикновени. Това ще ви позволи да видите същите основи на градусите и значително ще опростите решението.
Сега нека преминем към по-сложни уравнения, в които има различни бази, които по принцип не са сводими една към друга с помощта на степени.
Използване на свойството експонента
Нека ви напомня, че имаме две по-строги уравнения:
\[\begin(подравняване)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2,7)^(1-x))=0,09. \\\край (подравняване)\]
Основната трудност тук е, че не е ясно какво и до какво основание да се доведе. Къде са фиксираните изрази? Къде са общите основания? Няма нищо от това.
Но нека се опитаме да вървим по другия път. Ако няма готови идентични бази, можете да опитате да ги намерите, като разложите наличните бази.
Да започнем с първото уравнение:
\[\begin(подравняване)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& 21=7\cdot 3\Стрелка надясно ((21)^(3x))=((\left(7\cdot 3 \right))^(3x))=((7)^(3x))\ cdot ((3)^(3x)). \\\край (подравняване)\]
Но в края на краищата можете да направите обратното - съставете числото 21 от числата 7 и 3. Особено лесно е да направите това отляво, тъй като индикаторите на двете степени са еднакви:
\[\begin(подравняване)& ((7)^(x+6))\cdot ((3)^(x+6))=((\left(7\cdot 3 \right))^(x+ 6 ))=((21)^(x+6)); \\& ((21)^(x+6))=((21)^(3x)); \\&x+6=3x; \\& 2x=6; \\& x=3. \\\край (подравняване)\]
Това е всичко! Извадихте степента от продукта и веднага получихте красиво уравнение, което може да бъде решено в няколко реда.
Сега нека се заемем с второто уравнение. Тук всичко е много по-сложно:
\[((100)^(x-1))\cdot ((2,7)^(1-x))=0,09\]
\[((100)^(x-1))\cdot ((\left(\frac(27)(10) \right))^(1-x))=\frac(9)(100)\]
В този случай дробите се оказаха неприводими, но ако нещо може да се намали, не забравяйте да го намалите. Това често води до интересни основания, с които вече можете да работите.
За съжаление не сме измислили нищо. Но виждаме, че експонентите вляво в произведението са противоположни:
Позволете ми да ви напомня: за да се отървете от знака минус в степента, просто трябва да „обърнете“ дроба. Така че нека пренапишем оригиналното уравнение:
\[\begin(align)& ((100)^(x-1))\cdot ((\left(\frac(10)(27) \right))^(x-1))=\frac(9 )(100); \\& ((\left(100\cdot \frac(10)(27) \right))^(x-1))=\frac(9)(100); \\& ((\left(\frac(1000)(27) \right))^(x-1))=\frac(9)(100). \\\край (подравняване)\]
Във втория ред просто поставихме в скоби общата сума от продукта според правилото $((a)^(x))\cdot ((b)^(x))=((\left(a\cdot b \right) ))^ (x))$, а в последния просто умножиха числото 100 с дроб.
Сега имайте предвид, че числата отляво (в основата) и отдясно са донякъде сходни. Как? Да, очевидно: те са степени от едно и също число! Ние имаме:
\[\begin(align)& \frac(1000)(27)=\frac(((10)^(3)))(((3)^(3)))=((\left(\frac( 10)(3) \вдясно))^(3)); \\& \frac(9)(100)=\frac(((3)^(2)))(((10)^(3)))=((\left(\frac(3)(10) \вдясно))^(2)). \\\край (подравняване)\]
По този начин нашето уравнение ще бъде пренаписано, както следва:
\[((\left((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=((\left(\frac(3) )(10) \вдясно))^(2))\]
\[((\left((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=((\left(\frac(10) )(3) \вдясно))^(3\left(x-1 \right)))=((\left(\frac(10)(3) \right))^(3x-3))\]
В същото време вдясно можете да получите и степен със същата основа, за която е достатъчно просто да „превърнете“ дроба:
\[((\left(\frac(3)(10) \right))^(2))=((\left(\frac(10)(3) \right))^(-2))\]
Накрая нашето уравнение ще приеме вида:
\[\begin(подравняване)& ((\left(\frac(10)(3) \right))^(3x-3))=((\left(\frac(10)(3) \right)) ^(-2)); \\& 3x-3=-2; \\& 3x=1; \\& x=\frac(1)(3). \\\край (подравняване)\]
Това е цялото решение. Основната му идея се свежда до това, че дори и с различни причини, ние се опитваме да сведем тези причини до една и съща. В това ни помагат елементарни трансформации на уравнения и правилата за работа със степените.
Но какви правила и кога да използвате? Как да разберем, че в едно уравнение трябва да разделите двете страни на нещо, а в друго - да разложите основата на експоненциалната функция на фактори?
Отговорът на този въпрос ще дойде с опит. Опитайте се отначало с прости уравнения, а след това постепенно усложнявайте задачите - и много скоро вашите умения ще бъдат достатъчни, за да решите всяко експоненциално уравнение от същото USE или всяка независима / тестова работа.
И за да ви помогна в тази трудна задача, предлагам да изтеглите набор от уравнения на моя уебсайт за независимо решение. Всички уравнения имат отговори, така че винаги можете да проверите сами.
Общо взето, желая ви успешно обучение. И ще се видим в следващия урок - там ще анализираме наистина сложни експоненциални уравнения, където описаните по-горе методи вече не са достатъчни. И една проста тренировка също няма да е достатъчна. :)
Към youtube канала на сайта ни, за да сте наясно с всички нови видео уроци.
Първо, нека си припомним основните формули за степени и техните свойства.
Продукт на число асе случва само по себе си n пъти, можем да запишем този израз като a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n / a m \u003d a n - m
Степен или експоненциални уравнения- това са уравнения, в които променливите са в степени (или експоненти), а основата е число.
Примери за експоненциални уравнения:
В този пример числото 6 е основата, винаги е отдолу и променливата хстепен или мярка.
Нека да дадем повече примери за експоненциални уравнения.
2 x *5=10
16x-4x-6=0
Сега нека разгледаме как се решават експоненциални уравнения?
Да вземем едно просто уравнение:
2 х = 2 3
Такъв пример може да бъде решен дори в ума. Вижда се, че x=3. В крайна сметка, за да са равни лявата и дясната страна, трябва да поставите числото 3 вместо x.
Сега нека видим как трябва да се вземе това решение:
2 х = 2 3
х = 3
За да решим това уравнение, ние го премахнахме същите основания(тоест двойки) и написах каквото е останало, това са степени. Получихме отговора, който търсихме.
Сега нека обобщим нашето решение.
Алгоритъм за решаване на експоненциалното уравнение:
1. Трябва да се провери същотодали основите на уравнението отдясно и отляво. Ако основанията не са еднакви, търсим варианти за решаване на този пример.
2. След като основите са еднакви, приравнявамстепен и решете полученото ново уравнение.
Сега нека решим няколко примера:
Да започнем просто.
Основите от лявата и дясната страна са равни на числото 2, което означава, че можем да изхвърлим основата и да изравним техните степени.
x+2=4 Получи се най-простото уравнение.
х=4 - 2
х=2
Отговор: x=2
В следващия пример можете да видите, че основите са различни, това са 3 и 9.
3 3x - 9 x + 8 = 0
Като начало прехвърляме деветката в дясната страна, получаваме:
Сега трябва да направите същите основи. Знаем, че 9=3 2 . Нека използваме формулата за мощност (a n) m = a nm .
3 3x \u003d (3 2) x + 8
Получаваме 9 x + 8 = (3 2) x + 8 \u003d 3 2 x + 16
3 3x \u003d 3 2x + 16 сега е ясно, че основите от лявата и дясната страна са еднакви и равни на три, което означава, че можем да ги изхвърлим и да изравним степените.
3x=2x+16 получава най-простото уравнение
3x-2x=16
х=16
Отговор: x=16.
Нека разгледаме следния пример:
2 2x + 4 - 10 4 x \u003d 2 4
На първо място, разглеждаме основите, основите са различни две и четири. И ние трябва да сме същите. Преобразуваме четворката по формулата (a n) m = a nm .
4 x = (2 2) x = 2 2x
И ние също използваме една формула a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Добавете към уравнението:
2 2x 2 4 - 10 2 2x = 24
Дадохме пример по същите причини. Но ни пречат други числа 10 и 24. Какво да правим с тях? Ако се вгледате внимателно, можете да видите, че от лявата страна повтаряме 2 2x, ето отговора - можем да поставим 2 2x извън скоби:
2 2x (2 4 - 10) = 24
Нека изчислим израза в скоби:
2 4 — 10 = 16 — 10 = 6
Разделяме цялото уравнение на 6:
Представете си 4=2 2:
2 2x \u003d 2 2 основи са еднакви, изхвърлете ги и приравнете степените.
2x \u003d 2 се оказа най-простото уравнение. Разделяме го на 2, получаваме
х = 1
Отговор: х = 1.
Нека решим уравнението:
9 x - 12*3 x +27= 0
Нека трансформираме:
9 x = (3 2) x = 3 2x
Получаваме уравнението:
3 2x - 12 3 x +27 = 0
Основите са едни и същи за нас, равни на 3. В този пример се вижда, че първата тройка има степен два пъти (2x) от втората (само x). В този случай можете да решите метод на заместване. Числото с най-малка степен се заменя с:
Тогава 3 2x = (3 x) 2 = t 2
Заменяме всички степени с x в уравнението с t:
t 2 - 12t + 27 \u003d 0
Получаваме квадратно уравнение. Решаваме чрез дискриминанта, получаваме:
D=144-108=36
t1 = 9
t2 = 3
Обратно към променлива х.
Вземаме t 1:
t 1 = 9 = 3 x
Това е,
3 х = 9
3 х = 3 2
х 1 = 2
Един корен беше намерен. Търсим втория, от t 2:
t 2 \u003d 3 = 3 x
3 х = 3 1
х 2 = 1
Отговор: x 1 \u003d 2; х 2 = 1.
На сайта можете в секцията ПОМОГНЕТЕ ЗА РЕШЕНИЕТОАко имате въпроси, определено ще ви отговорим.
Присъединете се към група