Задачи, свързани с обратни тригонометрични функции, често се предлагат на изпитите в училище и на приемните изпити в някои университети. Подробно изучаване на тази тема може да се постигне само в извънкласни часове или в избираеми дисциплини. Предложеният курс е предназначен да развие възможно най-пълно способностите на всеки ученик, да подобри математическата му подготовка.
Курсът е предназначен за 10 часа:
1. Функции на arcsin x, arccos x, arctg x, arcctg x (4 часа).
2. Операции върху обратни тригонометрични функции (4 часа).
3. Обратни тригонометрични операции върху тригонометрични функции (2 часа).
Урок 1 (2 часа) Тема: Функции y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.
Цел: пълно отразяване на този въпрос.
1. Функция y \u003d arcsin x.
а) За функцията y \u003d sin x на сегмента има обратна (еднозначна) функция, която се съгласихме да наречем арксинус и да я обозначим, както следва: y = arcsin x. Графиката на обратната функция е симетрична с графиката на главната функция по отношение на симетралата на I - III координатни ъгли.
Свойства на функцията y = arcsin x .
1)Обхват на дефиницията: сегмент [-1; един];
2) Зона на промяна: рязане;
3) Функция y = arcsin x нечетно: arcsin (-x) = - arcsin x;
4) Функцията y = arcsin x е монотонно нарастваща;
5) Графиката пресича осите Ox, Oy в началото.
Пример 1. Намерете a = arcsin . Този пример може да бъде формулиран подробно, както следва: намерете такъв аргумент a , лежащ в диапазона от до , чийто синус е равен на .
Решение. Има безброй аргументи, чийто синус е например: 
и т.н. Но ние се интересуваме само от аргумента, който е на интервала. Този аргумент ще бъде. Така, .
Пример 2. Намерете 
.Решение.Аргументирайки по същия начин, както в пример 1, получаваме 
.
б) устни упражнения. Намерете: arcsin 1, arcsin (-1), arcsin , arcsin (), arcsin , arcsin (), arcsin , arcsin (), arcsin 0 Примерен отговор: 
, защото 
. Имат ли смисъл изразите: ; arcsin 1,5; 
?
в) Подредете във възходящ ред: arcsin, arcsin (-0,3), arcsin 0,9.
II. Функции y = arccos x, y = arctg x, y = arcctg x (по подобен начин).
Урок 2 (2 часа) Тема: Обратни тригонометрични функции, техните графики.
Цел: в този урок е необходимо да се изработят умения за определяне на стойностите на тригонометричните функции, за начертаване на обратни тригонометрични функции с помощта на D (y), E (y) и необходимите трансформации.
В този урок изпълнете упражнения, които включват намиране на областта на дефиниция, обхвата на функциите от типа: y = arcsin , y = arccos (x-2), y = arctg (tg x), y = arccos .
Необходимо е да се построят графики на функции: а) y = arcsin 2x; б) y = 2 arcsin 2x; в) y \u003d arcsin;
г) y \u003d arcsin; д) y = arcsin; е) y = arcsin; ж) y = | arcsin | .
Пример.Нека начертаем y = arccos
Можете да включите следните упражнения в домашната си работа: изградете графики на функции: y = arccos , y = 2 arcctg x, y = arccos | х | .
Графики на обратни функции
Урок №3 (2 часа) Тема:
Операции върху обратни тригонометрични функции.Цел: разширяване на математическите знания (това е важно за кандидатстващите в специалности с повишени изисквания за математическа подготовка) чрез въвеждане на основните съотношения за обратни тригонометрични функции.
Материал на урока.
Някои прости тригонометрични операции върху обратни тригонометрични функции: sin (arcsin x) \u003d x, i xi? един; cos (arсcos x) = x, i xi? един; tg (arctg x)= x , x I R; ctg (arcctg x) = x , x I R.
Упражнения.
а) tg (1,5 + arctg 5) = - ctg (arctg 5) = 
.
ctg (arctgx) = ; tg (arctg x) = .
б) cos (+ arcsin 0,6) = - cos (arcsin 0,6). Нека arcsin 0,6 \u003d a, sin a \u003d 0,6;
cos(arcsin x) = ; sin (arccos x) = .
Забележка: вземаме знака „+“ пред корена, защото a = arcsin x удовлетворява .
в) sin (1,5 + arcsin).Отговор:;
г) ctg ( + arctg 3) Отговор: ;
д) tg (- arcctg 4).Отговор: .
е) cos (0,5 + arccos) . Отговор: .
Изчисли:
а) грях (2 арктан 5) .
Нека arctg 5 = a, тогава sin 2 a = 
или sin(2 arctan 5) = 
;
б) cos (+ 2 arcsin 0,8) Отговор: 0,28.
в) arctg + arctg.
Нека a = arctg , b = arctg ,
тогава tan(a + b) = 
.
г) грях (арксин + арксин).
д) Докажете, че за всички x I [-1; 1] true arcsin x + arccos x = .
доказателство:
arcsin x = - arccos x
sin (arcsin x) = sin (- arccos x)
x = cos (arccos x)
За самостоятелно решение: sin (arccos ), cos (arcsin ) , cos (arcsin ()), sin (arctg (- 3)), tg (arccos ) , ctg (arccos ).
За домашно решение: 1) sin (arcsin 0.6 + arctg 0); 2) arcsin + arcsin; 3) ctg ( - arccos 0,6); 4) cos (2 arcctg 5) ; 5) sin (1,5 - arcsin 0,8); 6) arctg 0,5 - arctg 3.
Урок No 4 (2 часа) Тема: Операции върху обратни тригонометрични функции.
Цел: в този урок да се покаже използването на съотношения при преобразуване на по-сложни изрази.
Материал на урока.
УСТНО:
а) sin (arccos 0,6), cos (arcsin 0,8);
б) tg (arctg 5), ctg (arctg 5);
в) sin (arctg -3), cos (arctg ());
г) tg (arccos), ctg (arccos()).
НАПИСАНО:
1) cos (arcsin + arcsin + arcsin).
2) cos (arctg 5 - arccos 0,8) = cos (arctg 5) cos (arctg 0,8) + sin (arctg 5) sin (arccos 0,8) =
3) tg (- arcsin 0,6) = - tg (arcsin 0,6) = 
4) 
Самостоятелната работа ще помогне да се определи нивото на усвояване на материала
| 1) tg ( arctg 2 - arctg ) 2) cos( - arctg2) 3) arcsin + arccos |
1) cos (арксин + арксин) 2) грях (1.5 - arctg 3) 3) arcctg3 - arctg 2 |
За домашна работа можете да предложите:
1) ctg (arctg + arctg + arctg); 2) sin 2 (arctg 2 - arcctg ()); 3) sin (2 arctg + tg ( arcsin )); 4) грях (2 арктан); 5) tg ( (арксин))
Урок No 5 (2ч) Тема: Обратни тригонометрични операции върху тригонометрични функции.
Цел: формиране на разбирането на учениците за обратните тригонометрични операции върху тригонометричните функции, фокусиране върху повишаване на смислеността на изучаваната теория.
При изучаване на тази тема се приема, че обемът на теоретичния материал за запомняне е ограничен.
Материал за урока:
Можете да започнете да учите нов материал, като разгледате функцията y = arcsin (sin x) и я начертаете.
3. Всеки x I R е свързан с y I , т.е.<= y <= такое, что sin y = sin x.
4. Функцията е нечетна: sin (-x) \u003d - sin x; arcsin(sin(-x)) = - arcsin(sin x).
6. Графика y = arcsin (sin x) върху:
а) 0<= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .
б)<= x <= получим y = arcsin (sin x) = arcsin ( - x) = - x, ибо
sin y = sin ( - x) = sinx, 0<= - x <= .
Така, 
След като изградим y = arcsin (sin x) върху , ние продължаваме симетрично около началото на [- ; 0], като се вземе предвид нечетността на тази функция. Използвайки периодичност, продължаваме към цялата числова ос.
След това запишете някои съотношения: arcsin (sin a) = a if<= a <= ; arccos (cos а ) = a, ако е 0<= a <= ; arctg (tg a) = a if< a < ; arcctg (ctg a) = a , если 0 < a < .
И направете следните упражнения: а) arccos (sin 2) Отговор: 2 - ; б) arcsin (cos 0,6) Отговор: - 0,1; в) arctg (tg 2) Отговор: 2 -;
г) arcctg (tg 0,6) Отговор: 0,9; д) arccos (cos ( - 2)).Отговор: 2 -; е) арксин (sin (- 0,6)). Отговор: - 0,6; g) arctg (tg 2) = arctg (tg (2 - )). Отговор: 2 - ; h) arcctg (tg 0,6). Отговор: - 0,6; - арктанкс; д) arccos + arccos
Обратни тригонометрични функцииса арксинус, арккосинус, арктангенс и арккотангенс.
Нека първо дадем определения.
арксинусИли можем да кажем, че това е такъв ъгъл, принадлежащ на отсечката, чийто синус е равен на числото a.
Дъгов косинусчисло а се нарича число такова, че
Арктангенсчисло а се нарича число такова, че
Дъгова допирателначисло а се нарича число такова, че
Нека поговорим подробно за тези четири нови за нас функции - обратна тригонометрична.
Не забравяйте, че вече се срещнахме с .
Например, аритметичният квадратен корен от a е неотрицателно число, чийто квадрат е a.
Логаритъмът на числото b спрямо основата a е число c такова, че
При което
Разбираме защо математиците трябваше да „измислят“ нови функции. Например, решенията на едно уравнение са и Не бихме могли да ги запишем без специалния аритметичен символ квадратен корен.
Концепцията за логаритъма се оказа необходима, за да се напишат решения, например на такова уравнение: Решението на това уравнение е ирационално число.Това е степента, до която трябва да се повиши 2, за да се получи 7.
Същото е и с тригонометричните уравнения. Например искаме да решим уравнението
Ясно е, че решенията му отговарят на точки от тригонометричния кръг, чиято ордината е равна на И е ясно, че това не е таблична стойност на синуса. Как да запиша решения?
Тук не можем без нова функция, обозначаваща ъгъла, чийто синус е равен на дадено число a. Да, всички вече се досетиха. Това е арксинусът.
Ъгълът, принадлежащ на отсечката, чийто синус е равен, е арксинус на една четвърт. И така, поредицата от решения на нашето уравнение, съответстваща на дясната точка на тригонометричния кръг, е
И втората серия от решения на нашето уравнение е
Повече за решаването на тригонометрични уравнения -.
Остава да се изясни - защо в определението на арксинуса е посочено, че това е ъгъл, принадлежащ на отсечката?
Факт е, че има безкрайно много ъгли, чийто синус е например . Трябва да изберем един от тях. Избираме този, който лежи на сегмента.
Погледнете тригонометричния кръг. Ще видите, че на сегмента всеки ъгъл отговаря на определена стойност на синуса и само един. И обратно, всяка стойност на синуса от сегмента съответства на една стойност на ъгъла на сегмента. Това означава, че на сегмента можете да дефинирате функция, която приема стойности от до
Нека повторим отново определението:
Арксинусът на а е числото , такъв, че
Обозначение: Областта на дефиниране на арксинуса е сегмент. Диапазонът от стойности е сегмент.
Можете да си спомните израза "арксините живеят отдясно". Само не забравяме, че не само вдясно, но и в сегмента.
Готови сме да изобразим функцията
Както обикновено, маркираме x-стойностите по хоризонталната ос и y-стойностите по вертикалната ос.
Тъй като следователно, x лежи между -1 и 1.
Следователно областта на функцията y = arcsin x е сегментът
Казахме, че y принадлежи на отсечката. Това означава, че обхватът на функцията y = arcsin x е сегментът.
Обърнете внимание, че графиката на функцията y=arcsinx е поставена в областта, ограничена от линии и
Както винаги, когато начертаваме непозната функция, нека започнем с таблица.
По дефиниция арксинусът на нула е число от отсечката, чийто синус е нула. Какво е това число? - Ясно е, че това е нула.
По същия начин арксинусът на единица е числото от отсечката, чийто синус е равен на единица. Очевидно това
Продължаваме: - това е число от отсечката, чийто синус е равен на. да то
| 0 | |||||
| 0 |
Изграждаме функционална графика
Свойства на функцията
1. Област на дефиниция
2. Обхват от стойности
3. , тоест тази функция е нечетна. Неговата графика е симетрична по отношение на началото.
4. Функцията е монотонно нарастваща. Най-малката му стойност, равна на - , се постига при , а най-голямата му стойност, равна на , при
5. Какво е общото между графиките на функциите? Не мислите ли, че са „направени по един и същи образец“ – също като десния клон на функцията и графиката на функцията, или като графиките на експоненциалната и логаритмичната функции?
Представете си, че изрязваме малък фрагмент от до от обикновена синусоида и след това го обръщаме вертикално - и получаваме арксинусната графика.
Фактът, че за функцията на този интервал са стойностите на аргумента, тогава за арксинуса ще има стойностите на функцията. Така трябва да бъде! В крайна сметка синусът и арксинусът са взаимно обратни функции. Други примери за двойки взаимно обратни функции са за и , и експоненциалната и логаритмичната функции.
Припомнете си, че графиките на взаимно обратни функции са симетрични спрямо правата линия
По подобен начин дефинираме функцията.Само сегментът, от който се нуждаем, е такъв, на който всяка стойност на ъгъла съответства на собствената си стойност на косинус, и като знаем косинуса, можем да намерим еднозначно ъгъла. Имаме нужда от разрез
Дъговият косинус на a е числото , такъв, че
Лесно е да се запомни: „дъговите косинуси живеят отгоре“ и не само отгоре, а на сегмент
Обозначение: Област на дефиниране на дъгата косинус - сегмент Диапазон от стойности - сегмент
Очевидно сегментът е избран, защото върху него всяка стойност на косинус се взема само веднъж. С други думи, всяка косинусова стойност от -1 до 1 съответства на една стойност на ъгъла от интервала
Аркосинусът не е нито четна, нито нечетна функция. Вместо това можем да използваме следната очевидна връзка:
Нека начертаем функцията
Нуждаем се от част от функцията, където тя е монотонна, тоест приема всяка от стойностите си точно веднъж.
Нека изберем сегмент. На този сегмент функцията монотонно намалява, тоест съответствието между множествата и е едно към едно. Всяка стойност на x има своя собствена стойност на y. На този сегмент има функция, обратна на косинуса, тоест функцията y \u003d arccosx.
Попълнете таблицата, като използвате определението на дъгата косинус.
Аркосинусът на числото x, принадлежащ на интервала, ще бъде такова число y, принадлежащо на интервала, че
Така че, защото ;
Защото ;
защото ,
защото ,
| 0 | |||||
| 0 |
Ето сюжета на арккосинуса:
Свойства на функцията
1. Област на дефиниция
2. Обхват от стойности
Това е обща функция - тя не е нито четна, нито нечетна.
4. Функцията е строго намаляваща. Функцията y \u003d arccosx приема най-голямата стойност, равна на , при , а най-малката стойност, равна на нула, приема при
5. Функциите и са взаимно обратни.
Следващите са дъгова допирателна и дъгова допирателна.
Дъговата тангенс на a е числото , такъв, че
Обозначаване: . Областта на дефиниране на дъговата допирателна е интервалът. Диапазонът от стойности е интервалът.
Защо краищата на интервала - точки са изключени в определението на дъговата допирателна? Разбира се, защото допирателната в тези точки не е дефинирана. Няма число а, равно на тангенса на нито един от тези ъгли.
Нека начертаем дъговата допирателна. Според дефиницията дъговата тангенс на число x е число y, принадлежащо на интервала , така че
Как да се изгради графика вече е ясно. Тъй като арктангенсът е обратната функция на допирателната, действаме по следния начин:
Избираме такъв участък от графиката на функциите, където съответствието между x и y е едно към едно. Това е интервалът C. В този раздел функцията приема стойности от до
Тогава обратната функция, тоест функцията, домейнът на дефиниция ще бъде цялата числова права, от до, а областта на стойностите е интервалът
означава,
означава,
означава,
Но какво се случва, ако x е безкрайно голямо? С други думи, как се държи тази функция, когато x клони към плюс безкрайност?
Можем да си зададем въпроса: за кое число в интервала стойността на допирателната клони към безкрайност? - Очевидно това
Така че, за безкрайно големи стойности на x, графиката на дъговата допирателна се доближава до хоризонталната асимптота
По същия начин, тъй като x клони към минус безкрайност, графиката на дъговата допирателна се доближава до хоризонталната асимптота
На фигурата - графика на функцията
Свойства на функцията
1. Област на дефиниция
2. Обхват от стойности
3. Функцията е нечетна.
4. Функцията е строго нарастваща.
6. Функциите и са взаимно обратни - разбира се, когато функцията се разглежда на интервала
По подобен начин дефинираме функцията на котангенса на дъгата и начертаваме нейната графика.
Дъговата тангенс на a е числото , такъв, че
Графика на функциите:
Свойства на функцията
1. Област на дефиниция
2. Обхват от стойности
3. Функцията е в общ вид, тоест не е нито четна, нито нечетна.
4. Функцията е строго намаляваща.
5. Директни и - хоризонтални асимптоти на дадената функция.
6. Функции и са взаимно обратни, ако се разглеждат на интервала
Обратни тригонометрични функции(кръгови функции, дъгови функции) - математически функции, които са обратни на тригонометричните функции.
Те обикновено включват 6 функции:
- арксинус(символ: arcsin x; arcsin xе ъгълът гряхкоето е равно на х),
- арккосинус(символ: arccos x; arccos xе ъгълът, чийто косинус е равен хи така нататък),
- дъгова допирателна(символ: arctg xили арктан х),
- дъгова допирателна(символ: arcctg xили арккот хили аркотан х),
- дъгово сечение(символ: arcsec x),
- арккосеканс(символ: arccosec xили arccsc x).
Арксинус (y = arcsin x) е обратната функция на грях (х = синус 
. С други думи, връща ъгъла по неговата стойност грях.
Дъгов косинус (y = arccos x) е обратната функция на cos (x = cos y cos.
Арктангенс (y = арктан x) е обратната функция на tg (x = tgy), който има област на дефиниция и набор от стойности 
. С други думи, връща ъгъла по неговата стойност tg.
Дъгова допирателна (y = arcctg x) е обратната функция на ctg (x = ctg y), който има домейн на дефиниция и набор от стойности. С други думи, връща ъгъла по неговата стойност ctg.
ъглова секунда- arcsecant, връща ъгъла по стойността на неговата секанс.
arccosec- arccosecant, връща ъгъла по стойността на неговия косеканс.
Когато обратната тригонометрична функция не е дефинирана в определената точка, тогава нейната стойност няма да се появи в получената таблица. Функции ъглова секундаи arccosecне са дефинирани на отсечката (-1,1), но дъгов гряхи arccosса дефинирани само на интервала [-1,1].
Името на обратната тригонометрична функция се образува от името на съответната тригонометрична функция чрез добавяне на префикса "ковчег-" (от лат. дъга нас- дъга). Това се дължи на факта, че геометрично стойността на обратната тригонометрична функция е свързана с дължината на дъгата на единична окръжност (или ъгъла, който стяга тази дъга), която съответства на един или друг сегмент.
Понякога в чуждестранната литература, както и в научните / инженерните калкулатори, те използват обозначения като грях −1, cos -1за арксинуса, аркосинуса и други подобни - това се счита за не напълно точно, т.к вероятно объркване с повдигане на функция до степен −1 (« −1 » (минус първата степен) дефинира функцията x=f-1(y), обратно на функцията y=f(x)).
Основни отношения на обратните тригонометрични функции.
Тук е важно да се обърне внимание на интервалите, за които са валидни формулите.
Формули, свързани с обратни тригонометрични функции.
Означете всяка от стойностите на обратните тригонометрични функции чрез Arcsin x, Arccos x, Арктан х, Arccot xи запазете нотацията: arcsin x, arcos x, арктан х, арккот хза техните основни ценности, то връзката между тях се изразява чрез такива отношения.
Уроци 32-33. Обратни тригонометрични функции
09.07.2015 8936 0Цел: разгледа обратните тригонометрични функции, тяхното използване за писане на решения на тригонометрични уравнения.
I. Съобщаване на темата и целите на уроците
II. Изучаване на нов материал
1. Обратни тригонометрични функции
Нека започнем тази тема със следния пример.
Пример 1
Нека решим уравнението:а) sin x = 1/2; б) sin x \u003d a.
а) По оста на ординатите заложете стойността 1/2 и начертайте ъглитех 1 и x2, за коетогрях х = 1/2. В този случай x1 + x2 = π, откъдето x2 = π –х 1 . Според таблицата със стойностите на тригонометричните функции намираме стойността x1 = π/6, тогава
Отчитаме периодичността на функцията синус и записваме решенията на това уравнение:
където k ∈ Z .
б) Очевидно е, че алгоритъмът за решаване на уравнениетогрях x = a е същото като в предишния параграф. Разбира се, сега стойността на a се начертава по оста y. Има нужда по някакъв начин да се обозначи ъгълът x1. Договорихме се да обозначаваме такъв ъгъл със символадъгов грях а. Тогава решенията на това уравнение могат да се запишат катоТези две формули могат да се комбинират в една:при което 
По подобен начин се въвеждат и други обратни тригонометрични функции.
Много често е необходимо да се определи стойността на ъгъла от известната стойност на неговата тригонометрична функция. Такава задача е многозначна - има безкраен брой ъгли, чиито тригонометрични функции са равни на една и съща стойност. Следователно, въз основа на монотонността на тригонометричните функции, се въвеждат следните обратни тригонометрични функции за еднозначно определяне на ъглите.
Арксинус на a (арксин , чийто синус е равен на a, т.е.
Дъгов косинус на число a(arccos а) - такъв ъгъл a от интервала, чийто косинус е равен на a, т.е.
Дъга тангенс на число a(arctg а) - такъв ъгъл a от интервалачиято допирателна е a, т.е.
tg a = a.
Дъга тангенс на число a(arctg а) - такъв ъгъл a от интервала (0; π), чийто котангенс е равен на a, т.е. ctg a = a.
Пример 2
Да намерим:
Като се имат предвид дефинициите на обратните тригонометрични функции, получаваме:
Пример 3
Изчислете 
Нека ъгъл a = arcsin 3/5, тогава по дефиниция sin a = 3/5 и . Следователно, ние трябва да намерим cos а. Използвайки основната тригонометрична идентичност, получаваме:
Взето е предвид, че cos a ≥ 0. И така, 
Свойства на функцията | Функция |
|||
y = arcsin x | y = arccos x | y = arctg x | y = arcctg x |
|
домейн | x ∈ [-1; един] | x ∈ [-1; един] | x ∈ (-∞; +∞) | x ∈ (-∞ +∞) |
Диапазон от стойности | y ∈ [-π/2 ; π/2] | y ∈ | y ∈ (-π/2 ; π /2 ) | y ∈ (0; π) |
Паритет | странно | Нито четно, нито нечетно | странно | Нито четно, нито нечетно |
Нули на функцията (y = 0) | Когато х = 0 | За х = 1 | Когато х = 0 | y ≠ 0 |
Интервали на постоянство | y > 0 за x ∈ (0; 1], в< 0 при х ∈ [-1; 0) | y > 0 за x ∈ [-1; един) | y > 0 за x ∈ (0; +∞), в< 0 при х ∈ (-∞; 0) | y > 0 за x ∈ (-∞; +∞) |
Монотонно | Повишаване на | Намалява | Повишаване на | Намалява |
Връзка с тригонометричната функция | sin y \u003d x | cos y = x | tg y = x | ctg y=x |
График | ||||
Нека дадем редица типични примери, свързани с дефинициите и основните свойства на обратните тригонометрични функции.
Пример 4
Намерете домейна на функцията
За да бъде дефинирана функцията y, е необходимо неравенството
което е еквивалентно на системата от неравенства
Решението на първото неравенство е интервалът x∈
(-∞; +∞), вторият -Тази празнина и е решение на системата от неравенства, а оттам и областта на функцията
Пример 5
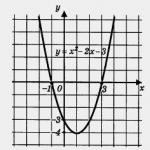
Намерете областта на промяна на функцията
Помислете за поведението на функцията z \u003d 2x - x2 (виж фигурата).
Вижда се, че z ∈ (-∞; 1]. Като се има предвид, че аргументът z функцията на обратната допирателна варира в определените граници, от данните в таблицата получаваме това
По този начин зоната на промяна
Пример 6
Нека докажем, че функцията y = arctg x нечетно. Позволявам
Тогава tg a \u003d -x или x \u003d - tg a \u003d tg (- a) и 
Следователно, - a \u003d arctg x или a \u003d - arctg Х. Така виждаме товат.е., y(x) е нечетна функция.
Пример 7
Ние изразяваме чрез всички обратни тригонометрични функции
Позволявам 
Очевидно е, че 
След това, тъй като
Нека представим ъгъл 
Защото 
тогава 
По същия начин, следователно 
и 
Така,
Пример 8
Нека построим графика на функцията y = cos (арксин x).
След това обозначете \u003d arcsin x 
Вземаме предвид, че x = sin a и y = cos a, т.е. x 2 + y2 = 1 и ограничения върху x (x∈
[-един; 1]) и y (y ≥ 0). Тогава графиката на функцията y = cos(arcsin x) е полукръг.
Пример 9
Нека построим графика на функцията y = arccos (cosx).
Тъй като функцията cos x промени на сегмента [-1; 1], тогава функцията y се дефинира по цялата реална ос и се променя на интервала . Ще имаме предвид, че y = arccos(cosx) \u003d x на сегмента; функцията y е четна и периодична с период 2π. Като се има предвид, че функцията има тези свойства cos x , Сега е лесно да се начертае.
Отбелязваме някои полезни равенства:
Пример 10
Намерете най-малката и най-голямата стойност на функциятаОзначете 
тогава 
Вземете функция 
Тази функция има минимум в точката z = π/4 и е равно на 
Максималната стойност на функцията се достига в точката z = -π/2 и е равно на 
По този начин и
Пример 11
Нека решим уравнението
Ние отчитаме това 
Тогава уравнението изглежда така:
или 
където По дефиниция на тангенса на дъгата получаваме:
2. Решение на най-простите тригонометрични уравнения
Подобно на пример 1, можете да получите решения на най-простите тригонометрични уравнения.
Уравнението | Решение |
tgx = a | |
ctg x = a |
Пример 12
Нека решим уравнението 
Тъй като функцията синус е нечетна, ние записваме уравнението във формата
Решения на това уравнение:
къде намираме 
Пример 13
Нека решим уравнението 
Съгласно горната формула, ние записваме решенията на уравнението:
и намерете 
Имайте предвид, че в частни случаи (a = 0; ±1) при решаване на уравненията sin x = a и cos x \u003d но е по-лесно и по-удобно да използвате не общи формули, а да пишете решения въз основа на единичен кръг:
за решението на уравнението sin x = 1
за уравнението sin x \u003d 0 решения x \u003d π k;
за решението на уравнението sin x = -1 
за уравнението cos x = 1 решения x = 2π k;
за решението на уравнението cos x = 0
за решението на уравнението cos x = -1 
Пример 14
Нека решим уравнението 
Тъй като в този пример има специален случай на уравнението, ние записваме решението, използвайки подходящата формула:
къде намираме 
III. Контролни въпроси (фронтална анкета)
1. Дефинирайте и избройте основните свойства на обратните тригонометрични функции.
2. Дайте графики на обратни тригонометрични функции.
3. Решение на най-простите тригонометрични уравнения.
IV. Задача в уроците
§ 15, № 3 (а, б); 4 (в, г); 7(а); 8(а); 12(b); 13(а); 15 (с); 16(а); 18 (а, б); 19 (в); 21;
§ 16, № 4 (а, б); 7(а); 8 (б); 16 (а, б); 18(а); 19 (в, г);
§ 17, № 3 (а, б); 4 (в, г); 5 (а, б); 7 (в, г); 9 (б); 10 (а, в).
V. Домашна работа
§ 15, бр.3 (в, г); 4 (а, б); 7 (в); 8 (б); 12(а); 13(b); 15 (d); 16(b); 18 (в, г); 19 (d); 22;
§ 16, бр.4 (в, г); 7(b); 8(а); 16 (в, г); 18(b); 19 (а, б);
§ 17, бр.3 (в, г); 4 (а, б); 5 (в, г); 7 (а, б); 9 (г); 10 (б, г).
VI. Творчески задачи
1. Намерете обхвата на функцията:
Отговори :
2. Намерете обхвата на функцията:
Отговори:
3. Графика на функцията:
VII. Обобщаване на уроците
Обратните тригонометрични функции са математически функции, които са обратни на тригонометричните функции.
Функция y=arcsin(x)
Арксинусът на числото α е такова число α от интервала [-π/2;π/2], чийто синус е равен на α.
Графика на функциите
Функцията y \u003d sin (x) на отсечката [-π / 2; π / 2], е строго нарастваща и непрекъсната; следователно, той има обратна функция, която е строго нарастваща и непрекъсната.
Обратната функция за функцията y= sin(x), където x ∈[-π/2;π/2], се нарича арксинус и се обозначава y=arcsin(x), където x∈[-1;1 ].
И така, според дефиницията на обратната функция, областта на дефиницията на арксинуса е сегментът [-1; 1], а наборът от стойности е сегментът [-π/2; π/2].
Обърнете внимание, че графиката на функцията y=arcsin(x), където x ∈[-1;1]. е симетрична на графиката на функцията y= sin(x), където x∈[-π/2;π /2], по отношение на симетралата на координатните ъгли първа и трета четвърт.
Обхватът на функцията y=arcsin(x).
Пример номер 1.
Намерете arcsin(1/2)?
Тъй като диапазонът на функцията arcsin(x) принадлежи на интервала [-π/2;π/2], подходяща е само стойността π/6. Следователно arcsin(1/2) = π/6.
Отговор: π/6
Пример №2.
Намерете arcsin(-(√3)/2)?
Тъй като диапазонът на arcsin(x) x ∈[-π/2;π/2] е подходяща само стойността -π/3. Следователно arcsin(-(√3)/2) =- π/3.
Функция y=arccos(x)
Арккосинусът на число α е число α от интервала, чийто косинус е равен на α.
Графика на функциите
Функцията y= cos(x) на интервала е строго намаляваща и непрекъсната; следователно той има обратна функция, която е строго намаляваща и непрекъсната.
Извиква се обратната функция за функцията y= cosx, където x ∈ дъга косинуси означава y=arccos(x), където x ∈[-1;1].
И така, според дефиницията на обратната функция, областта на дефиницията на арккосинуса е сегментът [-1; 1], а наборът от стойности е сегментът.
Забележете, че графиката на функцията y=arccos(x), където x ∈[-1;1] е симетрична на графиката на функцията y= cos(x), където x ∈, по отношение на ъглополовящата на координатни ъгли на първата и третата четвърт.
Обхватът на функцията y=arccos(x).
Пример №3.
Намерете arccos(1/2)?
Тъй като обхватът на arccos(x) е x∈, подходяща е само стойността π/3. Следователно arccos(1/2) =π/3.
Пример номер 4.
Намерете arccos(-(√2)/2)?
Тъй като обхватът на функцията arccos(x) принадлежи на интервала , подходяща е само стойността 3π/4. Следователно arccos(-(√2)/2) =3π/4.
Отговор: 3π/4
Функция y=arctg(x)
Дъговата допирателна на число α е такова число α от интервала [-π/2; π/2], чиято тангенс е равна на α.
Графика на функциите 
Функцията на допирателната е непрекъсната и строго нарастваща на интервала (-π/2; π/2); следователно той има обратна функция, която е непрекъсната и строго нарастваща.
Обратната функция за функцията y= tg(x), където x∈(-π/2;π/2); се нарича арктангенс и означава y=arctg(x), където x∈R.
И така, според дефиницията на обратната функция, областта на дефиниране на арктангенса е интервалът (-∞; +∞), а наборът от стойности е интервалът
(-π/2;π/2).
Забележете, че графиката на функцията y=arctg(x), където x∈R, е симетрична на графиката на функцията y=tgx, където x ∈ (-π/2;π/2), по отношение на симетралата на координатните ъгли на първата и третата четвърт.
Обхватът на функцията y=arctg(x).
Пример №5?
Намерете arctg((√3)/3).
Тъй като диапазонът на arctan(x) x ∈(-π/2;π/2), е подходяща само стойността π/6. Следователно arctg((√3)/3) =π/6.
Пример номер 6.
Намерете arctg(-1)?
Тъй като диапазонът на arctg(x) x ∈(-π/2;π/2), е подходяща само стойността -π/4. Следователно arctg(-1) = - π/4.
Функция y=arctg(x)
Дъговата тангенс на число α е такова число α от интервала (0; π), чийто котангенс е равен на α.
Графика на функциите
На интервала (0;π) котангенсната функция стриктно намалява; освен това той е непрекъснат във всяка точка от този интервал; следователно на интервала (0;π) тази функция има обратна функция, която е строго намаляваща и непрекъсната.
Обратната функция за функцията y=ctg(x), където x ∈(0;π), се нарича котангенс на дъгата и се означава y=arcctg(x), където x∈R.
И така, според дефиницията на обратната функция, областта на дефиниране на дъговата допирателна ще бъде R, а наборът от стойности ще бъде интервалът (0; π). ;π), по отношение на ъглополовящата на координатните ъгли на първата и третата четвърт.
Обхватът на функцията y=arcctg(x).
Пример номер 7.
Намерете arcctg((√3)/3)?
Тъй като диапазонът на arcctg(x) x ∈(0;π), подходяща е само стойността π/3. Следователно arccos((√3)/3) =π/3.
Пример номер 8.
Намерете arcctg(-(√3)/3)?
Тъй като диапазонът на arcctg(x) x∈(0;π), подходяща е само стойността 2π/3. Следователно arccos(-(√3)/3) =2π/3.
Редактори: Агеева Любов Александровна, Гаврилина Анна Викторовна
